Calculus I: Functions, Equations, and Inequalities Problems
VerifiedAdded on 2023/01/05
|16
|3507
|61
Homework Assignment
AI Summary
This document presents a comprehensive solution to a Calculus I assignment. The assignment covers a range of topics, including determining the domain and range of functions, working with exponential and logarithmic functions, finding the inverse of a function, solving equations and inequalities (linear and quadratic), analyzing circle equations, and working with trigonometric functions, including determining amplitude, period, and phase shift. The solution also includes problems involving finding the minimum cost of production using calculus, and solving for x and y in various equations. The assignment further explores composite functions and the analysis of polynomial functions, including finding x and y intercepts and end behavior.

1.
a)
h(t) = 5t + 7
h(t) is basically the function 5t shifted up by 7 units.It is therefore essentially an
exponential function.Exponential functions accept all real numbers as input, there-
fore domain of h(t) is:
Domain:(−∞, +∞)
Exponentialfunctions decay and tend to zero as t → −∞.Since 7 is added to the
exponential term, it will tend to 7 as t → −∞.Exponential functions tend to ∞ as
they grow.Therefore, range of h(t) is:
Range:(7, +∞)
b)
r(m) = 2 +
√ 3 − m
Square root of negative numbers is undefined, so 3−m cannot become less than zero.
3 − m = 0=⇒ m = 3, for m > 3,r(m) is undefined,so the function can accept
numbers less than 3.
Domain:[3, −∞)
As m → −∞, r(m) tends to +∞.The least value r(m) achieves when the square
root term becomes zero, at which its value is 2.
Range:[2, +∞)
2.
f (x) = 3
2x + 1
a) Inverse
Step 1:y = 3
2x + 1
Step 2:Interchange x and y
x = 3
2y + 1
a)
h(t) = 5t + 7
h(t) is basically the function 5t shifted up by 7 units.It is therefore essentially an
exponential function.Exponential functions accept all real numbers as input, there-
fore domain of h(t) is:
Domain:(−∞, +∞)
Exponentialfunctions decay and tend to zero as t → −∞.Since 7 is added to the
exponential term, it will tend to 7 as t → −∞.Exponential functions tend to ∞ as
they grow.Therefore, range of h(t) is:
Range:(7, +∞)
b)
r(m) = 2 +
√ 3 − m
Square root of negative numbers is undefined, so 3−m cannot become less than zero.
3 − m = 0=⇒ m = 3, for m > 3,r(m) is undefined,so the function can accept
numbers less than 3.
Domain:[3, −∞)
As m → −∞, r(m) tends to +∞.The least value r(m) achieves when the square
root term becomes zero, at which its value is 2.
Range:[2, +∞)
2.
f (x) = 3
2x + 1
a) Inverse
Step 1:y = 3
2x + 1
Step 2:Interchange x and y
x = 3
2y + 1
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Step 3:Solve for y
2y + 1 =
3
x =⇒ y = 1
2
3
x − 1
Step 4:y = f−1(x)
f −1(x) = 1
2
3
x − 1
Step 5:Verify:(f −1 o f )(x) = x
(f −1 o f ) =1
2
3
f (x) − 1
= 1
2
3
3
2x+1
− 1
!
= 1
2(2x + 1 − 1) = x =⇒ Verified
Therefore, inverse of f (x) is f−1(x) = 1
2
3
x − 1
b)
f (x) accepts allvalues ofx except the one for which 2x + 1 = 0,because at this
point value of f (x) is undefined.This point is x = −1
2. Therefore,
Domain: −∞, −1
2 ∪ −1
2, +∞
f (x) attains allvalues possible except 0 because the function tends to 0 as x gets
bigger and bigger but never actually reaches it.f (x) = 0 is an horizontal assymptote.
Range:(−∞, 0) ∪ (0, +∞)
c)
For an inverse function, the domain is just the range of f (x) and the range is domain
of f (x).Therefore,
Domain:(−∞, 0) ∪ (0, +∞)
Range: −∞, −1
2 ∪ −1
2, +∞
2y + 1 =
3
x =⇒ y = 1
2
3
x − 1
Step 4:y = f−1(x)
f −1(x) = 1
2
3
x − 1
Step 5:Verify:(f −1 o f )(x) = x
(f −1 o f ) =1
2
3
f (x) − 1
= 1
2
3
3
2x+1
− 1
!
= 1
2(2x + 1 − 1) = x =⇒ Verified
Therefore, inverse of f (x) is f−1(x) = 1
2
3
x − 1
b)
f (x) accepts allvalues ofx except the one for which 2x + 1 = 0,because at this
point value of f (x) is undefined.This point is x = −1
2. Therefore,
Domain: −∞, −1
2 ∪ −1
2, +∞
f (x) attains allvalues possible except 0 because the function tends to 0 as x gets
bigger and bigger but never actually reaches it.f (x) = 0 is an horizontal assymptote.
Range:(−∞, 0) ∪ (0, +∞)
c)
For an inverse function, the domain is just the range of f (x) and the range is domain
of f (x).Therefore,
Domain:(−∞, 0) ∪ (0, +∞)
Range: −∞, −1
2 ∪ −1
2, +∞

3.
f (x) = 3x2 + 1
a)
f (1) is the value of f (x) at x = 1.Therefore,
f (1) = 3(1)2 + 1 = 3 + 1 = 4
b)
f (1 + h) = 3(1 + h)2 + 1 = 3(1 + 2h + h2) + 1 = 3h2 + 6h + 4
c)
f (1) − f (1 + h)
h = 4 − (3h2 + 6h + 4)
h
= −3h2 − 6h
h
= −3h − 6
4.
x2 + y2 − 4x + 8y + 16 = 0
We want to reduce this equation into standard form of circle equation:(x − h)2 +
(y − k)2 = a2, where (h, k) is the circle center while a is the radius.
f (x) = 3x2 + 1
a)
f (1) is the value of f (x) at x = 1.Therefore,
f (1) = 3(1)2 + 1 = 3 + 1 = 4
b)
f (1 + h) = 3(1 + h)2 + 1 = 3(1 + 2h + h2) + 1 = 3h2 + 6h + 4
c)
f (1) − f (1 + h)
h = 4 − (3h2 + 6h + 4)
h
= −3h2 − 6h
h
= −3h − 6
4.
x2 + y2 − 4x + 8y + 16 = 0
We want to reduce this equation into standard form of circle equation:(x − h)2 +
(y − k)2 = a2, where (h, k) is the circle center while a is the radius.
You're viewing a preview
Unlock full access by subscribing today!

0 = x2 + y2 − 4x + 8y + 16
0 = x2 − 4x + y2 + 8y + 16
[Split 16 as 4+12]
0 = (x2 − 4x + 4) + y2 + 8y + 12
[Add 4 to both sides of the equation]
4 = (x2 − 4x + 4) + (y2 + 8y + 16)
[Terms in brackets are squares]
22 = (x − 2)2 + (y + 4)2
Comparing with standard form,we get:a = 2,h = 2 and k = −4.Therefore,the
circle has a center at (2, −4) and has a radius=2.
5.
a)
10 − 6x ≤ 14 − 4x
[Add 6x to both sides]
10 ≤ 14 + 2x
14 + 2x ≥ 10
[Subtract 14 from both sides]
2x ≥ −4
[Divide throughout by 2]
x ≥ −2
Therefore, solution to the inequality is:
x ∈ [−2, +∞)
0 = x2 − 4x + y2 + 8y + 16
[Split 16 as 4+12]
0 = (x2 − 4x + 4) + y2 + 8y + 12
[Add 4 to both sides of the equation]
4 = (x2 − 4x + 4) + (y2 + 8y + 16)
[Terms in brackets are squares]
22 = (x − 2)2 + (y + 4)2
Comparing with standard form,we get:a = 2,h = 2 and k = −4.Therefore,the
circle has a center at (2, −4) and has a radius=2.
5.
a)
10 − 6x ≤ 14 − 4x
[Add 6x to both sides]
10 ≤ 14 + 2x
14 + 2x ≥ 10
[Subtract 14 from both sides]
2x ≥ −4
[Divide throughout by 2]
x ≥ −2
Therefore, solution to the inequality is:
x ∈ [−2, +∞)
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

b)
x2 − 3x ≥ 10
[Subtract 10 from both sides]
x2 − 3x − 10 ≥ 0
x2 − 5x + 2x + −10 ≥ 0
(x − 5)(x + 2) ≥ 0
This condition (x − 5)(x + 2) ≥ 0 is satisfied when both the terms in the brackets
are positive, or both are negative or either one or both are zero.
i) Both terms positive:Implies x > 5 and x > −2.Therefore for x > 5, this condi-
tion is always true.
ii) Both terms negative:Implies x < 5 and x < −2.Therefore for x < −2,this
condition is always true.
iii) Zero condition:
x = 5 and/or x = −2 satisfies this condition, that is (x−5)(x+2) = 0 iv) −2 < x < 5
:
Between x = −2 and x = 5, the term x + 2 is positive but x − 5 is negative, therefore
this interval fails the inequality.
Solution to the inequality x2 − 3x ≥ 10, therefore, is:
x ∈ (−∞, −2] ∪ [5, +∞)
6.
The sine function:
f(t) = A sin (Bt + C) + D
has, amplitude = A, phase shift =C
D (to the left), and period =2π
B .
The given function is:
f (t) = 5 sin (3t − π) + 7
Comparing with standard form, we get:
a)
x2 − 3x ≥ 10
[Subtract 10 from both sides]
x2 − 3x − 10 ≥ 0
x2 − 5x + 2x + −10 ≥ 0
(x − 5)(x + 2) ≥ 0
This condition (x − 5)(x + 2) ≥ 0 is satisfied when both the terms in the brackets
are positive, or both are negative or either one or both are zero.
i) Both terms positive:Implies x > 5 and x > −2.Therefore for x > 5, this condi-
tion is always true.
ii) Both terms negative:Implies x < 5 and x < −2.Therefore for x < −2,this
condition is always true.
iii) Zero condition:
x = 5 and/or x = −2 satisfies this condition, that is (x−5)(x+2) = 0 iv) −2 < x < 5
:
Between x = −2 and x = 5, the term x + 2 is positive but x − 5 is negative, therefore
this interval fails the inequality.
Solution to the inequality x2 − 3x ≥ 10, therefore, is:
x ∈ (−∞, −2] ∪ [5, +∞)
6.
The sine function:
f(t) = A sin (Bt + C) + D
has, amplitude = A, phase shift =C
D (to the left), and period =2π
B .
The given function is:
f (t) = 5 sin (3t − π) + 7
Comparing with standard form, we get:
a)

Amplitude = A = 5
b)
Period =2π
B = 2π
3
c)
Phase shift =
C
B = −π
3, or π
3 to the right.
d)
f π
3 = 5 sin (3 ·
π
3 − π) + 7 = 5 sin (0) + 7 = 7
7.
a)
13 + 25e−x = 63
[Subtract 13 from both sides]
25e−x = 50
[Divide throughout by 25]
e−x = 2
[Apply log to both sides ]
ln (e−x) = ln (2)
[Property:ln (ea) = a]
−x = ln (2)=⇒ x = − ln (2)
[Property:ln (ab) = b ln (a)]
x = ln (2−1) = ln 1
2
b)
b)
Period =2π
B = 2π
3
c)
Phase shift =
C
B = −π
3, or π
3 to the right.
d)
f π
3 = 5 sin (3 ·
π
3 − π) + 7 = 5 sin (0) + 7 = 7
7.
a)
13 + 25e−x = 63
[Subtract 13 from both sides]
25e−x = 50
[Divide throughout by 25]
e−x = 2
[Apply log to both sides ]
ln (e−x) = ln (2)
[Property:ln (ea) = a]
−x = ln (2)=⇒ x = − ln (2)
[Property:ln (ab) = b ln (a)]
x = ln (2−1) = ln 1
2
b)
You're viewing a preview
Unlock full access by subscribing today!

log(x − 7) + log(x − 10) = 1
[Property:log(a) + log(b) = log(ab)]
log((x − 7) · (x − 10)) = 1
[log(10) = 1]
log((x − 7) · (x − 10)) = log(10)
[Taking terms out of logarithms]
(x − 7)(x − 10) = 10
x2 − 17x + 70 = 10
x2 − 17x + 60 = 0
x2 − 12x − 5x + 60 = 0
(x − 12)(x − 5) = 0 =⇒ x = 12 or x = 5
x = 5 is discarded as it creates negative logarithms (undefined).Therefore,the so-
lution to the equation is x = 12.
8.
Cost of production for x number of cars is:
C(x) = x2 − 36x + 10, 400
a)
At minimum Cost of production:
dC
dx = 0
dC
dx = d
dx(x2 − 36x + 10, 400) = 2x − 36
Therefore, for cost to be minimum:
2x − 36 = 0 =⇒ x = 18
18 cars produced daily will minimize cost of production.
b)
[Property:log(a) + log(b) = log(ab)]
log((x − 7) · (x − 10)) = 1
[log(10) = 1]
log((x − 7) · (x − 10)) = log(10)
[Taking terms out of logarithms]
(x − 7)(x − 10) = 10
x2 − 17x + 70 = 10
x2 − 17x + 60 = 0
x2 − 12x − 5x + 60 = 0
(x − 12)(x − 5) = 0 =⇒ x = 12 or x = 5
x = 5 is discarded as it creates negative logarithms (undefined).Therefore,the so-
lution to the equation is x = 12.
8.
Cost of production for x number of cars is:
C(x) = x2 − 36x + 10, 400
a)
At minimum Cost of production:
dC
dx = 0
dC
dx = d
dx(x2 − 36x + 10, 400) = 2x − 36
Therefore, for cost to be minimum:
2x − 36 = 0 =⇒ x = 18
18 cars produced daily will minimize cost of production.
b)
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

The minimum cost is:
C(18) = (18)2 − 36(18) + 10400 = 10076 $
9.
P = (−4, 6) and Q = (2, −2)
a)
Vertical line passing through Q.Vertical line passing through a point (a, b) is given
by the equation x = a,therefore for Q = (2, −2),vertical line passing through it is
x = 2
b)
Equation of line passing through P and Q.
Equation of a line passing through (x1, y1) is:
y − y1 = m(x − x1)
where, m is the slope of the line.
Since both P and Q lie on the line, slope of the line can be calculated as:
m = yP − yQ
xP − xQ
where, xP , yP are co-ordinates of P and similarly for Q.Therefore,
m = 6 − (−2)
−4 − 2 = −4
3
Therefore, equation of line passing through P = (−4, 6) and Q is:
y − 6 = −
4
3(x − (−4))=⇒ y − 6 = −
4
3(x + 4)
In the slope-intercept form, it is given as:
y = −
4
3(x + 4) + 6
c)
Slope of the line 5x − 2y = 4 is obtained by expressing it in standard slope-intercept
C(18) = (18)2 − 36(18) + 10400 = 10076 $
9.
P = (−4, 6) and Q = (2, −2)
a)
Vertical line passing through Q.Vertical line passing through a point (a, b) is given
by the equation x = a,therefore for Q = (2, −2),vertical line passing through it is
x = 2
b)
Equation of line passing through P and Q.
Equation of a line passing through (x1, y1) is:
y − y1 = m(x − x1)
where, m is the slope of the line.
Since both P and Q lie on the line, slope of the line can be calculated as:
m = yP − yQ
xP − xQ
where, xP , yP are co-ordinates of P and similarly for Q.Therefore,
m = 6 − (−2)
−4 − 2 = −4
3
Therefore, equation of line passing through P = (−4, 6) and Q is:
y − 6 = −
4
3(x − (−4))=⇒ y − 6 = −
4
3(x + 4)
In the slope-intercept form, it is given as:
y = −
4
3(x + 4) + 6
c)
Slope of the line 5x − 2y = 4 is obtained by expressing it in standard slope-intercept

for.
5x − 2y = 4 =⇒ 2y = 5x − 4 =⇒ y =
5
2x − 2
Slope, therefore is:m = 5
2.
Line perpendicular to the above line has a slope m0 which satisfies the condition:
m × m0 = −1
Implies, 5
2 m0 = −1 =⇒ m0 = −2
5
Equation of line passing through P = (−4, 6) with slope m0 = −2
5 is given by:
y − 6 = −
2
5(x − (−4)=⇒ y = −2
5(x + 4) + 6
10.
f (x) = ln x & g(x) = 10 − x
a)
(f o g)(x):
(f o g)(x) = ln g(x) = ln (10 − x)
b)
Domain of (f o g)(x) is the set of numbers for which 10 − x is greater than 0, because
the function is not defined for numbers less than or equal to 0.Therefore, 10 − x > 0
or x < 10 is valid input.Domain of (f o g)(x) is:
x ∈ (−∞, 10)
c)
(f o g)(9) = ln (10 − 9) = ln (1) = 0
5x − 2y = 4 =⇒ 2y = 5x − 4 =⇒ y =
5
2x − 2
Slope, therefore is:m = 5
2.
Line perpendicular to the above line has a slope m0 which satisfies the condition:
m × m0 = −1
Implies, 5
2 m0 = −1 =⇒ m0 = −2
5
Equation of line passing through P = (−4, 6) with slope m0 = −2
5 is given by:
y − 6 = −
2
5(x − (−4)=⇒ y = −2
5(x + 4) + 6
10.
f (x) = ln x & g(x) = 10 − x
a)
(f o g)(x):
(f o g)(x) = ln g(x) = ln (10 − x)
b)
Domain of (f o g)(x) is the set of numbers for which 10 − x is greater than 0, because
the function is not defined for numbers less than or equal to 0.Therefore, 10 − x > 0
or x < 10 is valid input.Domain of (f o g)(x) is:
x ∈ (−∞, 10)
c)
(f o g)(9) = ln (10 − 9) = ln (1) = 0
You're viewing a preview
Unlock full access by subscribing today!

11.
f (x) = (x + 1)(x − 2)(x − 4)2
a) x- intercept(s):
x- intercept(s) is the point(s) at which the function intersects the x- axis.It is found
by setting y = f (x) = 0, which is the equation of x- axis.
Therefore,
0 = (x + 1)(x − 2)(x − 4)2
This equation is satisfied when:x = −1, x = 2 or x = 4.This can be verified by
substituting for x in the equation.
Eg.
x = 4 =⇒ f(x) = (4 + 1)(4 − 2)(4 − 4)2 = 5 × 2 × 0 = 0
Similarly,other two values can also be verified.Therefore,the x- intercepts are
points −1, 2 and 4, on the x- axis.
b) y- intercept:
y- intercept(s) is the point(s) at which the function intersects the y- axis.It is found
by setting x = 0 in the function, which is the equation of y- axis.
Therefore, substituting x = 0 in f (x), we get:
f (x) = (0 + 1)(0 − 2)(0 − 4)2 = 1 × −2 × 16 = −32
Therefore, the y- intercept is the point −32 on the y- axis.
c) End behaviour:
In order to analyze f (x) let us first express it in the expanded form:
f (x) = (x + 1)(x − 2)(x − 4)2 = (x2 − x − 2)(x2 − 8x + 16) = x4 − 9x3 + 22x2 − 32
f (x) has a leading term with even degree (x4) having a positive coefficient (+1).
As x → ±∞, the highest degree term in the function f (x) will dominate and therefore
f (x) will behave like y = x4.
Since the leading term is an even degree term with positive coefficient:
x → +∞ =⇒ f(x) → +∞
x → −∞ =⇒ f(x) → +∞
f (x) = (x + 1)(x − 2)(x − 4)2
a) x- intercept(s):
x- intercept(s) is the point(s) at which the function intersects the x- axis.It is found
by setting y = f (x) = 0, which is the equation of x- axis.
Therefore,
0 = (x + 1)(x − 2)(x − 4)2
This equation is satisfied when:x = −1, x = 2 or x = 4.This can be verified by
substituting for x in the equation.
Eg.
x = 4 =⇒ f(x) = (4 + 1)(4 − 2)(4 − 4)2 = 5 × 2 × 0 = 0
Similarly,other two values can also be verified.Therefore,the x- intercepts are
points −1, 2 and 4, on the x- axis.
b) y- intercept:
y- intercept(s) is the point(s) at which the function intersects the y- axis.It is found
by setting x = 0 in the function, which is the equation of y- axis.
Therefore, substituting x = 0 in f (x), we get:
f (x) = (0 + 1)(0 − 2)(0 − 4)2 = 1 × −2 × 16 = −32
Therefore, the y- intercept is the point −32 on the y- axis.
c) End behaviour:
In order to analyze f (x) let us first express it in the expanded form:
f (x) = (x + 1)(x − 2)(x − 4)2 = (x2 − x − 2)(x2 − 8x + 16) = x4 − 9x3 + 22x2 − 32
f (x) has a leading term with even degree (x4) having a positive coefficient (+1).
As x → ±∞, the highest degree term in the function f (x) will dominate and therefore
f (x) will behave like y = x4.
Since the leading term is an even degree term with positive coefficient:
x → +∞ =⇒ f(x) → +∞
x → −∞ =⇒ f(x) → +∞
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

d) Sketch of f (x):
f (x) = (x + 1)(x − 2)(x − 4)2
Sign off (x) is the result ofsign ofthree terms:x + 1,x − 2 and (x − 4)2. For
example, if x < −1, then x − 1 is negative, x − 2 is negative and (x − 4)2 is positive,
therefore, sign of f (x) is (−)(−)(+) which is positive (+).
x f (x) sign
x < −1 (−)(−)(+) +
−1 < x < 2 (+)(−)(+) −
2 < x < 4 (+)(+)(+) +
x > 4 (+)(+)(+) +
Few points to plot on the graph:
x f (x) value
x = 0 (0 + 1)(0 − 2)(0 − 4)2 −32
x = 3 (3 + 1)(3 − 2)(3 − 4)2 4
Using these sample points,the intercept points and information on end behaviour,
f (x) is plotted and shown in figure below:
f (x) = (x + 1)(x − 2)(x − 4)2
Sign off (x) is the result ofsign ofthree terms:x + 1,x − 2 and (x − 4)2. For
example, if x < −1, then x − 1 is negative, x − 2 is negative and (x − 4)2 is positive,
therefore, sign of f (x) is (−)(−)(+) which is positive (+).
x f (x) sign
x < −1 (−)(−)(+) +
−1 < x < 2 (+)(−)(+) −
2 < x < 4 (+)(+)(+) +
x > 4 (+)(+)(+) +
Few points to plot on the graph:
x f (x) value
x = 0 (0 + 1)(0 − 2)(0 − 4)2 −32
x = 3 (3 + 1)(3 − 2)(3 − 4)2 4
Using these sample points,the intercept points and information on end behaviour,
f (x) is plotted and shown in figure below:

12.
To prove: 1
sin θ− sin θ = cot θ cos θ
1
sin θ− sin θ =
1 − sin2 θ
sin θ
[Identity: 1 = sin2 θ + cos2 θ]
= sin2 θ + cos2 θ − sin2 θ
sin θ
= cos2 θ
sin θ
= cos θ
sin θcos θ
= cot θ cos θ =⇒ Proved
13.
2 sin t cos t + cos t = 0∀ t ∈ [0, 2π)
0 = 2 sin t cos t + cos t
= cos t(2 sin t + 1)
=⇒ cos t = 0 or 2 sin t + 1 = 0
cos tbecomes 0 at t= 0.5π & 1.5π for t ∈ [0, 2π). The second condition is :
2 sin t + 1 = 0 or sin t = −0.5.This is true for t = 7π/6 & t = 11π/6 fort ∈ [0, 2π).
Therefore solution for the equation is:
t = {0.5π, 1.5π, 7π/6, 11π/6}
for t ∈ [0, 2π)
To prove: 1
sin θ− sin θ = cot θ cos θ
1
sin θ− sin θ =
1 − sin2 θ
sin θ
[Identity: 1 = sin2 θ + cos2 θ]
= sin2 θ + cos2 θ − sin2 θ
sin θ
= cos2 θ
sin θ
= cos θ
sin θcos θ
= cot θ cos θ =⇒ Proved
13.
2 sin t cos t + cos t = 0∀ t ∈ [0, 2π)
0 = 2 sin t cos t + cos t
= cos t(2 sin t + 1)
=⇒ cos t = 0 or 2 sin t + 1 = 0
cos tbecomes 0 at t= 0.5π & 1.5π for t ∈ [0, 2π). The second condition is :
2 sin t + 1 = 0 or sin t = −0.5.This is true for t = 7π/6 & t = 11π/6 fort ∈ [0, 2π).
Therefore solution for the equation is:
t = {0.5π, 1.5π, 7π/6, 11π/6}
for t ∈ [0, 2π)
You're viewing a preview
Unlock full access by subscribing today!
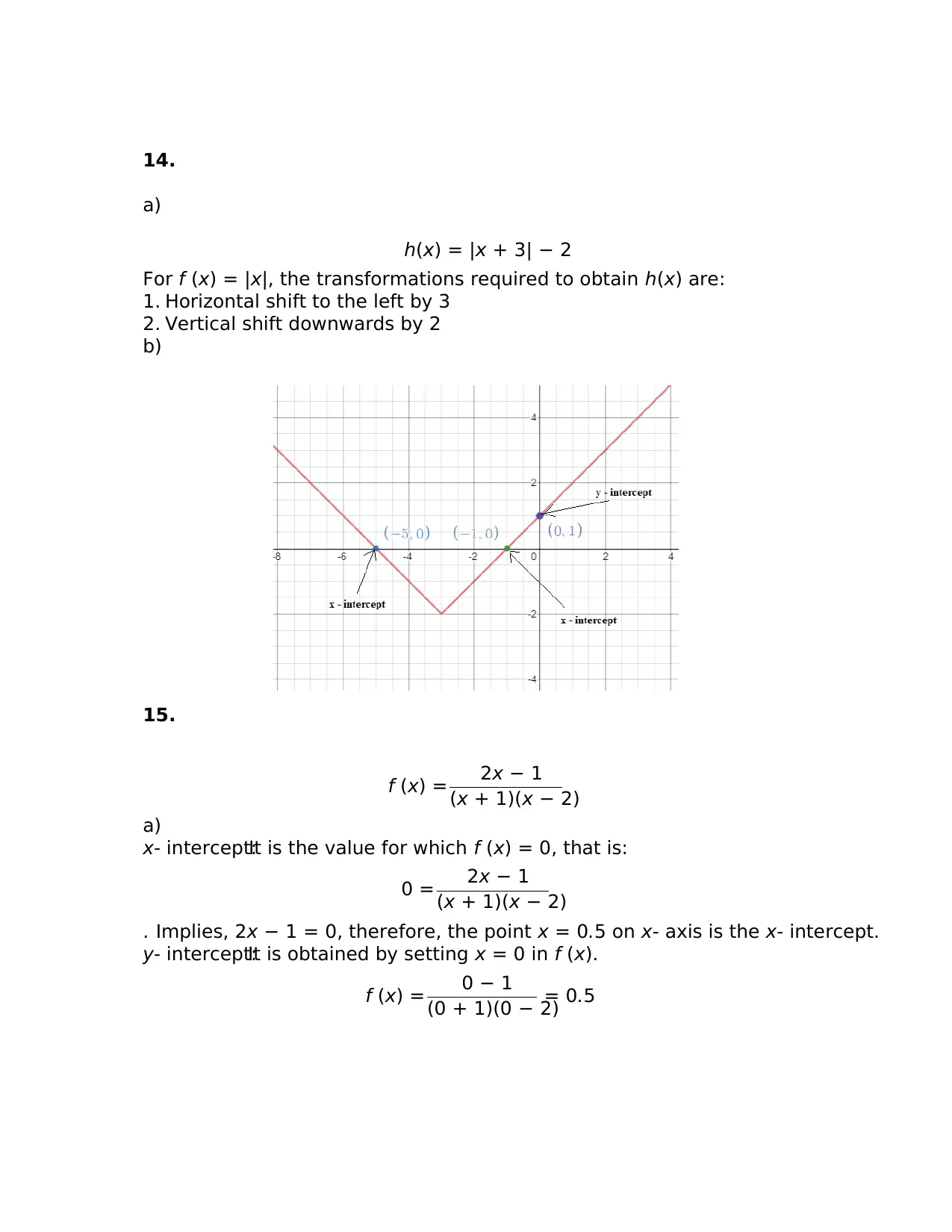
14.
a)
h(x) = |x + 3| − 2
For f (x) = |x|, the transformations required to obtain h(x) are:
1. Horizontal shift to the left by 3
2. Vertical shift downwards by 2
b)
15.
f (x) = 2x − 1
(x + 1)(x − 2)
a)
x- intercept:It is the value for which f (x) = 0, that is:
0 = 2x − 1
(x + 1)(x − 2)
. Implies, 2x − 1 = 0, therefore, the point x = 0.5 on x- axis is the x- intercept.
y- intercept:It is obtained by setting x = 0 in f (x).
f (x) = 0 − 1
(0 + 1)(0 − 2)
= 0.5
a)
h(x) = |x + 3| − 2
For f (x) = |x|, the transformations required to obtain h(x) are:
1. Horizontal shift to the left by 3
2. Vertical shift downwards by 2
b)
15.
f (x) = 2x − 1
(x + 1)(x − 2)
a)
x- intercept:It is the value for which f (x) = 0, that is:
0 = 2x − 1
(x + 1)(x − 2)
. Implies, 2x − 1 = 0, therefore, the point x = 0.5 on x- axis is the x- intercept.
y- intercept:It is obtained by setting x = 0 in f (x).
f (x) = 0 − 1
(0 + 1)(0 − 2)
= 0.5
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
. The point y = 0.5 on the y- axis is the y- intercept.
b)
Vertical asymptote(s) is the line for which the denominator becomes 0.For f (x), this
happens for x = −1 and x = 2.Therefore, equation of vertical asymptote is x = −1
and x = 2.
Since the degree of denominator is greater than that of the numerator,x- axis be-
comes horizontal asymptote to f (x).Therefore, equation of horizontal asymptote is
y = 0.
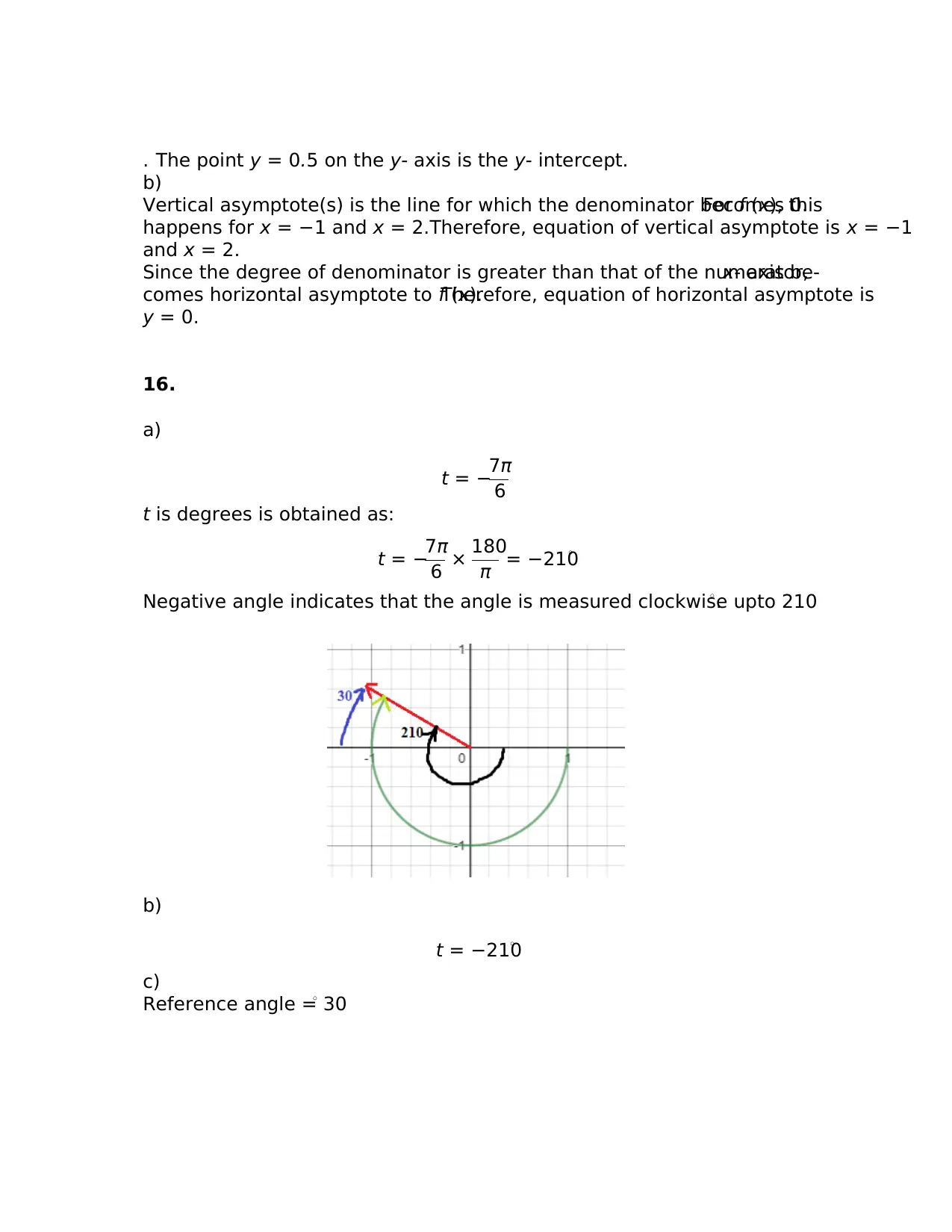
16.
a)
t = −7π
6
t is degrees is obtained as:
t = −7π
6 × 180
π = −210◦
Negative angle indicates that the angle is measured clockwise upto 210◦.
b)
t = −210◦
c)
Reference angle = 30◦
b)
Vertical asymptote(s) is the line for which the denominator becomes 0.For f (x), this
happens for x = −1 and x = 2.Therefore, equation of vertical asymptote is x = −1
and x = 2.
Since the degree of denominator is greater than that of the numerator,x- axis be-
comes horizontal asymptote to f (x).Therefore, equation of horizontal asymptote is
y = 0.
16.
a)
t = −7π
6
t is degrees is obtained as:
t = −7π
6 × 180
π = −210◦
Negative angle indicates that the angle is measured clockwise upto 210◦.
b)
t = −210◦
c)
Reference angle = 30◦

d)
cot(t) = cot(r)
where r is the reference angle.Therefore,
cot (t) =
adjacent
opposite
= x
y = −√ 3/2
1/2 = −√ 3
e)
sin−1(cos (t))
cos t = x = −
√ 3
2
but, sin (−60) = −
√ 3
2
Therefore,
sin−1(cos (t)) = sin−1(sin (−60)) = −60◦
cot(t) = cot(r)
where r is the reference angle.Therefore,
cot (t) =
adjacent
opposite
= x
y = −√ 3/2
1/2 = −√ 3
e)
sin−1(cos (t))
cos t = x = −
√ 3
2
but, sin (−60) = −
√ 3
2
Therefore,
sin−1(cos (t)) = sin−1(sin (−60)) = −60◦
You're viewing a preview
Unlock full access by subscribing today!

References:
1. Sepanski,M. R. (2010). Algebra. Providence,R.I., American Mathematical
Society.
http://public.eblib.com/choice/publicfullrecord.aspx?p=4718110.
2. Cohen, L., Theodore B.,Sklar, D. (2017).Precalculus.Cengage Learning.
1. Sepanski,M. R. (2010). Algebra. Providence,R.I., American Mathematical
Society.
http://public.eblib.com/choice/publicfullrecord.aspx?p=4718110.
2. Cohen, L., Theodore B.,Sklar, D. (2017).Precalculus.Cengage Learning.
1 out of 16
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.




