STM4PSD - Assignment 1: Statistical Analysis, Probability and R Code
VerifiedAdded on 2023/01/16
|7
|1641
|42
Homework Assignment
AI Summary
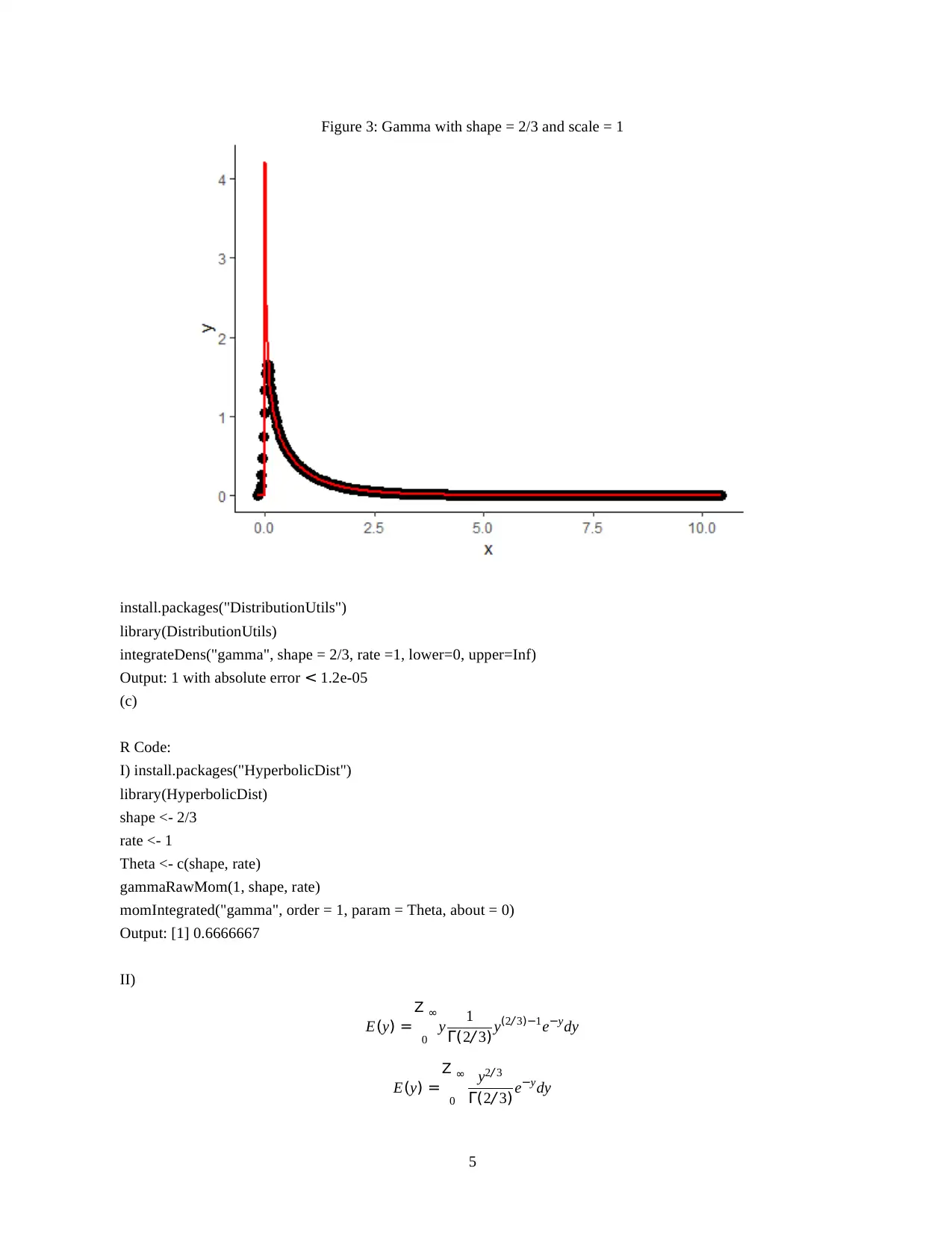
This document presents the solutions to STM4PSD Assignment 1, encompassing various statistical concepts and their applications. The assignment addresses probability calculations, including conditional probabilities in a sobriety checkpoint scenario, and the analysis of association rules using support, confidence, and lift. It further explores data analysis using R code, including frequency plots and the application of the gamma distribution, calculating expected values, and variances. Finally, it examines joint and marginal probabilities, and the calculation of probabilities based on a given joint distribution, including the construction of probability distributions for combined variables. The solutions incorporate R code snippets for data visualization and statistical calculations, providing a comprehensive guide to the topics covered in the assignment.
1 out of 7








![[object Object]](/_next/static/media/star-bottom.7253800d.svg)