University Computing Assessment: Data Analysis with Excel 2010
VerifiedAdded on 2023/04/06
|13
|1287
|119
Homework Assignment
AI Summary
This computing assessment solution involves quantitative data analysis using Excel 2010 to analyze spectrophotometric data and particle diameter ranges. The first problem utilizes ANOVA to assess variations in antiviral drug samples (EMT, TDF, RPV), calculating masses at different wavelengths based on spectrophotometer readings. The analysis includes hypothesis testing and interpretation of statistical significance. The second problem explores the Gaussian distribution of nanoparticles stabilized with sodium alginate and composite materials, comparing their frequency and particle diameter ranges. The assessment includes ANOVA, mean, and standard deviation calculations to determine statistical differences between the nanoparticles. Desklib offers similar solved assignments and study tools for students.

1
Computing Assessment
Name:
University Name:
Professor Name:
Computing Assessment
Name:
University Name:
Professor Name:
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
2
Problem 1
According to Manfroid J, Selman F et al.001, the photometric accuracy is
viewed as how close to the correct value is the measured absorbance of a
sample. This requires material of exactly known absorbance. A solution has
to be made up from the solid hence leading to potential errors and
variances.
Given the data from spectrophotometric test of a sample, you are to use the
ANOVA test to perform the quantitative analysis of the samples.
Hence statistical analysis was performed by one-way (or one-factor) analysis
of variance (ANOVA) using Excel 2010.It was assumed that (p<0.05) .
Hypothesis:
Ho: the null hypothesis that there is variation in the test result of the three
samples of the antiviral drugs i.e EMT, TDF, RPV.
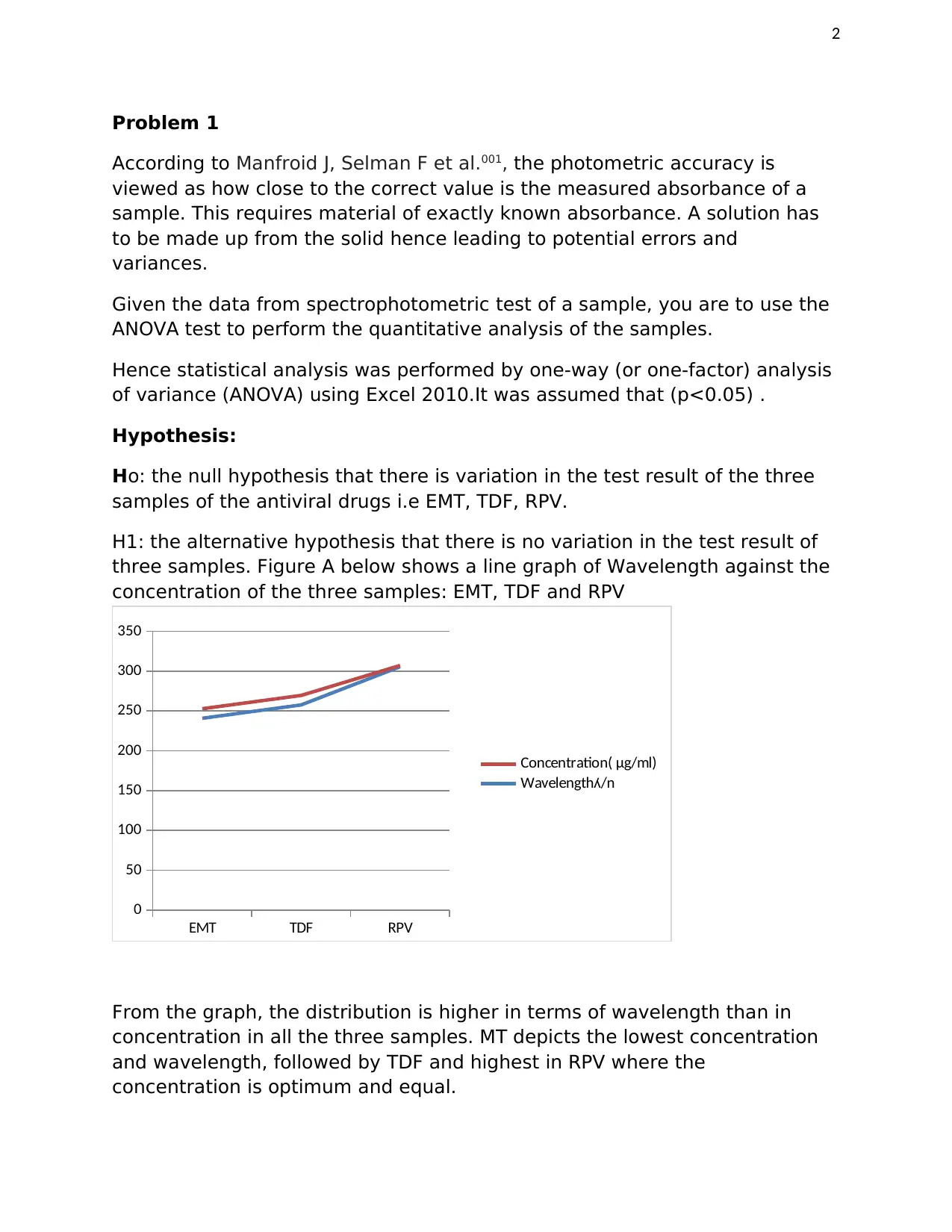
H1: the alternative hypothesis that there is no variation in the test result of
three samples. Figure A below shows a line graph of Wavelength against the
concentration of the three samples: EMT, TDF and RPV
EMT TDF RPV
0
50
100
150
200
250
300
350
Concentration( μg/ml)
Wavelengthʎ/n
From the graph, the distribution is higher in terms of wavelength than in
concentration in all the three samples. MT depicts the lowest concentration
and wavelength, followed by TDF and highest in RPV where the
concentration is optimum and equal.
Problem 1
According to Manfroid J, Selman F et al.001, the photometric accuracy is
viewed as how close to the correct value is the measured absorbance of a
sample. This requires material of exactly known absorbance. A solution has
to be made up from the solid hence leading to potential errors and
variances.
Given the data from spectrophotometric test of a sample, you are to use the
ANOVA test to perform the quantitative analysis of the samples.
Hence statistical analysis was performed by one-way (or one-factor) analysis
of variance (ANOVA) using Excel 2010.It was assumed that (p<0.05) .
Hypothesis:
Ho: the null hypothesis that there is variation in the test result of the three
samples of the antiviral drugs i.e EMT, TDF, RPV.
H1: the alternative hypothesis that there is no variation in the test result of
three samples. Figure A below shows a line graph of Wavelength against the
concentration of the three samples: EMT, TDF and RPV
EMT TDF RPV
0
50
100
150
200
250
300
350
Concentration( μg/ml)
Wavelengthʎ/n
From the graph, the distribution is higher in terms of wavelength than in
concentration in all the three samples. MT depicts the lowest concentration
and wavelength, followed by TDF and highest in RPV where the
concentration is optimum and equal.

3
Anova: Single Factor
SUMMARY
Groups Count
Su
m
Avera
ge
Varian
ce
ʎ/nm 3
80
4 268
1130.
88
3 0 0 0
EMT 3
0.8
57
0.285
667
0.032
35
TDF 3
0.4
89 0.163
0.020
307
RPV 3
0.3
19
0.106
333
0.004
666
TBL 3
1.2
74
0.424
667
0.046
566
ANOVA
Source of
Variation SS df MS F
P-
valu
e F crit
Between
Groups
17929
7.9 5
35859
.57
190.2
392
5.4E
-11
3.105
875
Within
Groups
2261.
968 12
188.4
973
Total
18155
9.8 17
Anova: Single Factor
SUMMARY
Groups Count
Su
m
Avera
ge
Varian
ce
ʎ/nm 3
80
4 268
1130.
88
3 0 0 0
EMT 3
0.8
57
0.285
667
0.032
35
TDF 3
0.4
89 0.163
0.020
307
RPV 3
0.3
19
0.106
333
0.004
666
TBL 3
1.2
74
0.424
667
0.046
566
ANOVA
Source of
Variation SS df MS F
P-
valu
e F crit
Between
Groups
17929
7.9 5
35859
.57
190.2
392
5.4E
-11
3.105
875
Within
Groups
2261.
968 12
188.4
973
Total
18155
9.8 17
You're viewing a preview
Unlock full access by subscribing today!
4
0.5 1 1.5 2 2.5 3 3.5
0
50
100
150
200
250
300
350
Wavelengthʎ/n
Concentration( μg/ml)
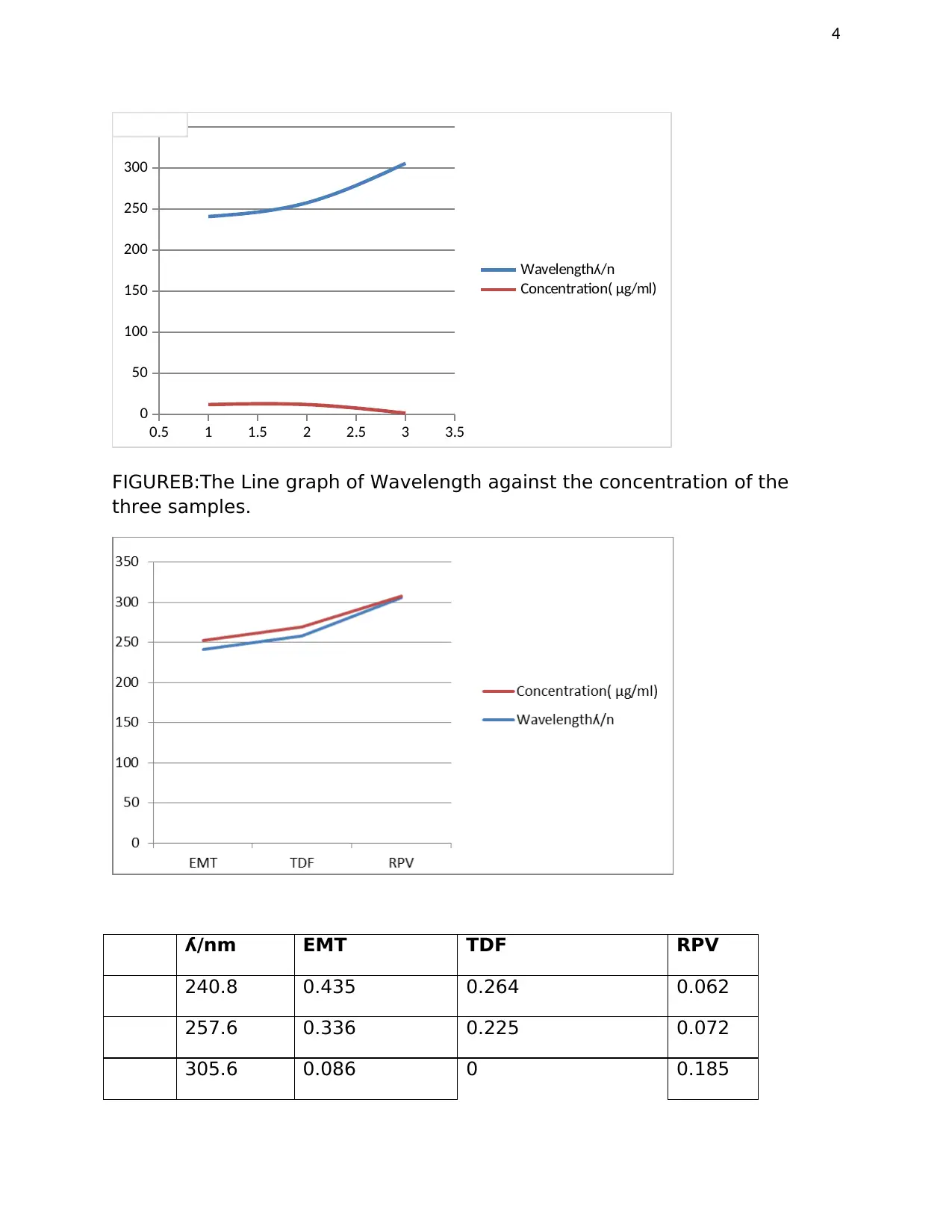
FIGUREB:The Line graph of Wavelength against the concentration of the
three samples.
ʎ/nm EMT TDF RPV
240.8 0.435 0.264 0.062
257.6 0.336 0.225 0.072
305.6 0.086 0 0.185
0.5 1 1.5 2 2.5 3 3.5
0
50
100
150
200
250
300
350
Wavelengthʎ/n
Concentration( μg/ml)
FIGUREB:The Line graph of Wavelength against the concentration of the
three samples.
ʎ/nm EMT TDF RPV
240.8 0.435 0.264 0.062
257.6 0.336 0.225 0.072
305.6 0.086 0 0.185
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
5
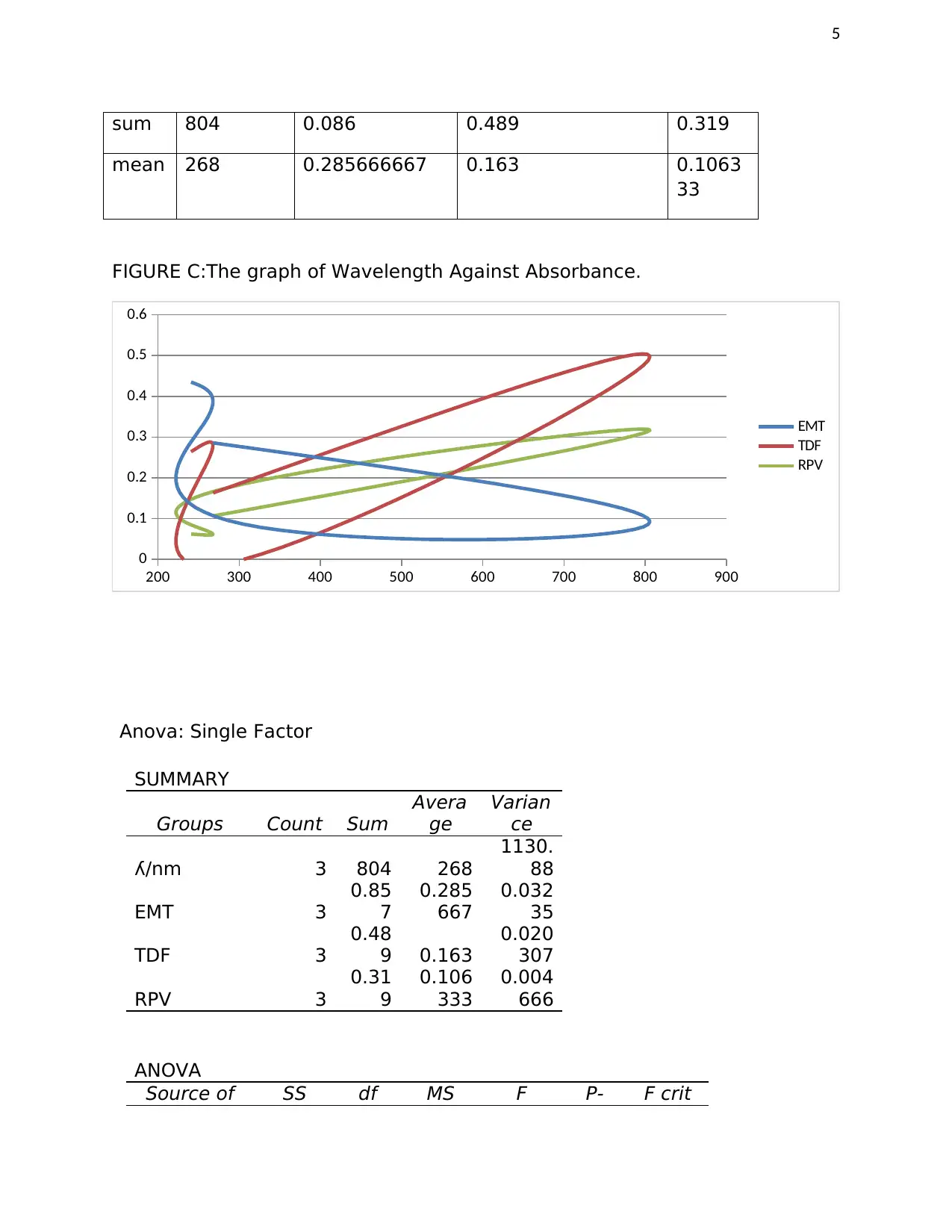
sum 804 0.086 0.489 0.319
mean 268 0.285666667 0.163 0.1063
33
FIGURE C:The graph of Wavelength Against Absorbance.
Anova: Single Factor
SUMMARY
Groups Count Sum
Avera
ge
Varian
ce
ʎ/nm 3 804 268
1130.
88
EMT 3
0.85
7
0.285
667
0.032
35
TDF 3
0.48
9 0.163
0.020
307
RPV 3
0.31
9
0.106
333
0.004
666
ANOVA
Source of SS df MS F P- F crit
200 300 400 500 600 700 800 900
0
0.1
0.2
0.3
0.4
0.5
0.6
EMT
TDF
RPV
sum 804 0.086 0.489 0.319
mean 268 0.285666667 0.163 0.1063
33
FIGURE C:The graph of Wavelength Against Absorbance.
Anova: Single Factor
SUMMARY
Groups Count Sum
Avera
ge
Varian
ce
ʎ/nm 3 804 268
1130.
88
EMT 3
0.85
7
0.285
667
0.032
35
TDF 3
0.48
9 0.163
0.020
307
RPV 3
0.31
9
0.106
333
0.004
666
ANOVA
Source of SS df MS F P- F crit
200 300 400 500 600 700 800 900
0
0.1
0.2
0.3
0.4
0.5
0.6
EMT
TDF
RPV

6
Variation
valu
e
Between
Groups
16138
1 3
53793
.67
190.2
623
8.93
E-08
4.066
181
Within
Groups
2261.
875 8
282.7
343
Total
16364
2.9 11
Test Statistic:
The p-value=8.93E-08 <alpha=0.05 hence H0 is statistically significant
different.
The critical value =4.066181 is on the left of the F value in the F distribution.
Hence F fall in the rejection region of the F distribution.
Generally, from the test statistic is statistically significant difference. Thus,
there is variation in the test result of the three samples.
In reference to the Contreras MD, Díaz-Madrigal S et al. 04 hypotheses, when
the Spectrophotometer is used in determining the concentration of a
substance, its statement is as below.
A=£ * I *C
Whereby,
A-IS the mass of the samples used in the new tablet.
£ -is the absorbance.
I – is the wavelength of the samples.
C –is the concentration of the absorbing species per unit data.
A240.8=0.435*240.8*12.0=1256.976mg
This is the mass of EMT at wavelength 240.8nm
A257.6=0.336*257.6*12.0=1038.6432mg
Variation
valu
e
Between
Groups
16138
1 3
53793
.67
190.2
623
8.93
E-08
4.066
181
Within
Groups
2261.
875 8
282.7
343
Total
16364
2.9 11
Test Statistic:
The p-value=8.93E-08 <alpha=0.05 hence H0 is statistically significant
different.
The critical value =4.066181 is on the left of the F value in the F distribution.
Hence F fall in the rejection region of the F distribution.
Generally, from the test statistic is statistically significant difference. Thus,
there is variation in the test result of the three samples.
In reference to the Contreras MD, Díaz-Madrigal S et al. 04 hypotheses, when
the Spectrophotometer is used in determining the concentration of a
substance, its statement is as below.
A=£ * I *C
Whereby,
A-IS the mass of the samples used in the new tablet.
£ -is the absorbance.
I – is the wavelength of the samples.
C –is the concentration of the absorbing species per unit data.
A240.8=0.435*240.8*12.0=1256.976mg
This is the mass of EMT at wavelength 240.8nm
A257.6=0.336*257.6*12.0=1038.6432mg
You're viewing a preview
Unlock full access by subscribing today!

7
The mass of EMT at wavelength 257.6
A305.6=0.086*305.6*1.5=1182.672mg.
The mass of EMT at wavelength 305.6nm
A240.8=0.264*240.8*12.09=762.8544mg
The mass of TDF at wavelength 240.8
A257.6=0.225*257.6*12.0=695.52mg
The mass of TDF at wavelength257.6
A305.6=0.00*305.6*1.5=0mg
The mass of TDF at wavelength 305.6
A240.8=0.062*240.8*12.0=179.1552mg
The mass of RPV at wavelength 240.8
A257.6=0.072*257.6*12.0=222.5664mg.
The mass of RPV at wavelength 257.6
A305.6=0.185*305.6*1.5=84.804mg
The mass of RPV at wavelength 305.6.
Problem 2
The mass of EMT at wavelength 257.6
A305.6=0.086*305.6*1.5=1182.672mg.
The mass of EMT at wavelength 305.6nm
A240.8=0.264*240.8*12.09=762.8544mg
The mass of TDF at wavelength 240.8
A257.6=0.225*257.6*12.0=695.52mg
The mass of TDF at wavelength257.6
A305.6=0.00*305.6*1.5=0mg
The mass of TDF at wavelength 305.6
A240.8=0.062*240.8*12.0=179.1552mg
The mass of RPV at wavelength 240.8
A257.6=0.072*257.6*12.0=222.5664mg.
The mass of RPV at wavelength 257.6
A305.6=0.185*305.6*1.5=84.804mg
The mass of RPV at wavelength 305.6.
Problem 2
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
8
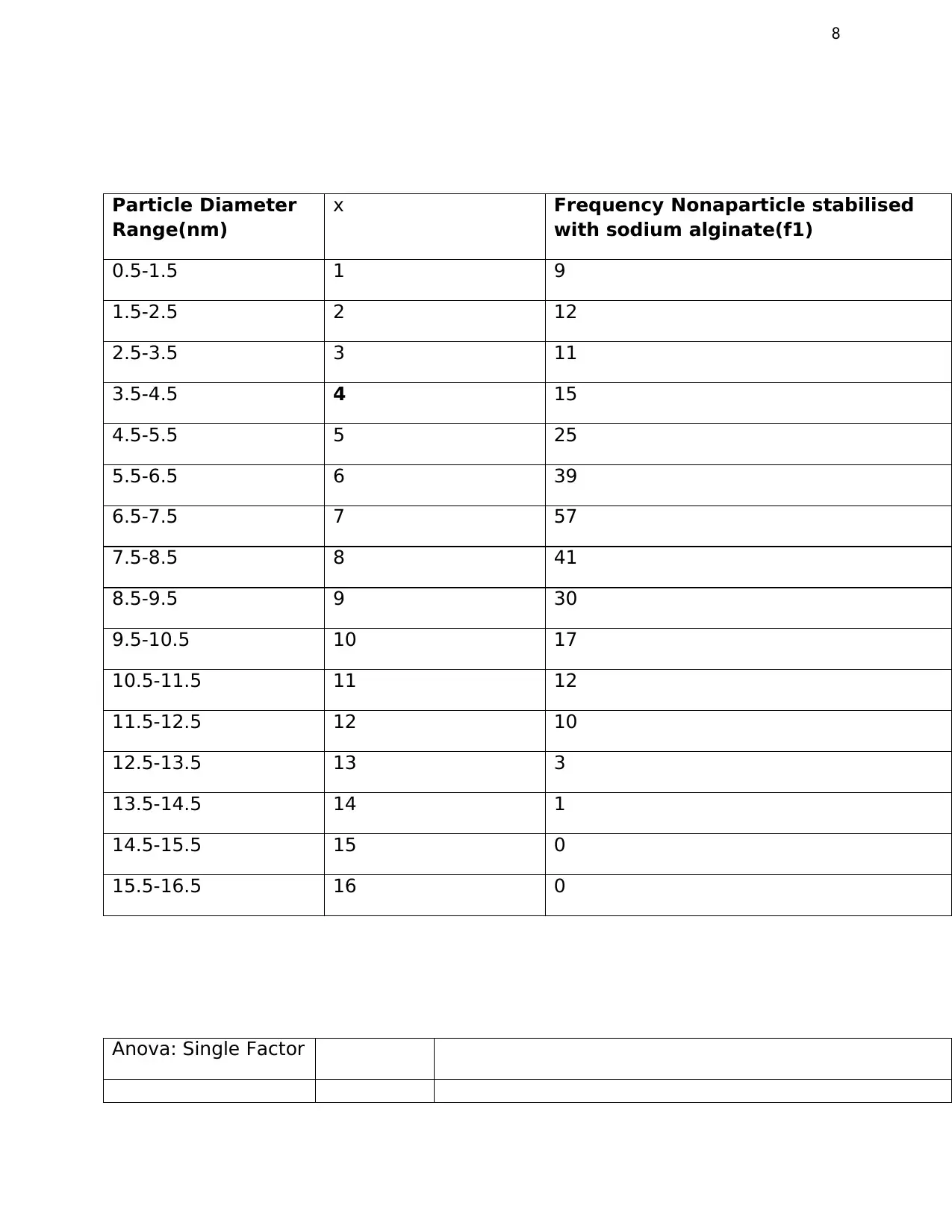
Particle Diameter
Range(nm)
x Frequency Nonaparticle stabilised
with sodium alginate(f1)
0.5-1.5 1 9
1.5-2.5 2 12
2.5-3.5 3 11
3.5-4.5 4 15
4.5-5.5 5 25
5.5-6.5 6 39
6.5-7.5 7 57
7.5-8.5 8 41
8.5-9.5 9 30
9.5-10.5 10 17
10.5-11.5 11 12
11.5-12.5 12 10
12.5-13.5 13 3
13.5-14.5 14 1
14.5-15.5 15 0
15.5-16.5 16 0
Anova: Single Factor
Particle Diameter
Range(nm)
x Frequency Nonaparticle stabilised
with sodium alginate(f1)
0.5-1.5 1 9
1.5-2.5 2 12
2.5-3.5 3 11
3.5-4.5 4 15
4.5-5.5 5 25
5.5-6.5 6 39
6.5-7.5 7 57
7.5-8.5 8 41
8.5-9.5 9 30
9.5-10.5 10 17
10.5-11.5 11 12
11.5-12.5 12 10
12.5-13.5 13 3
13.5-14.5 14 1
14.5-15.5 15 0
15.5-16.5 16 0
Anova: Single Factor
9
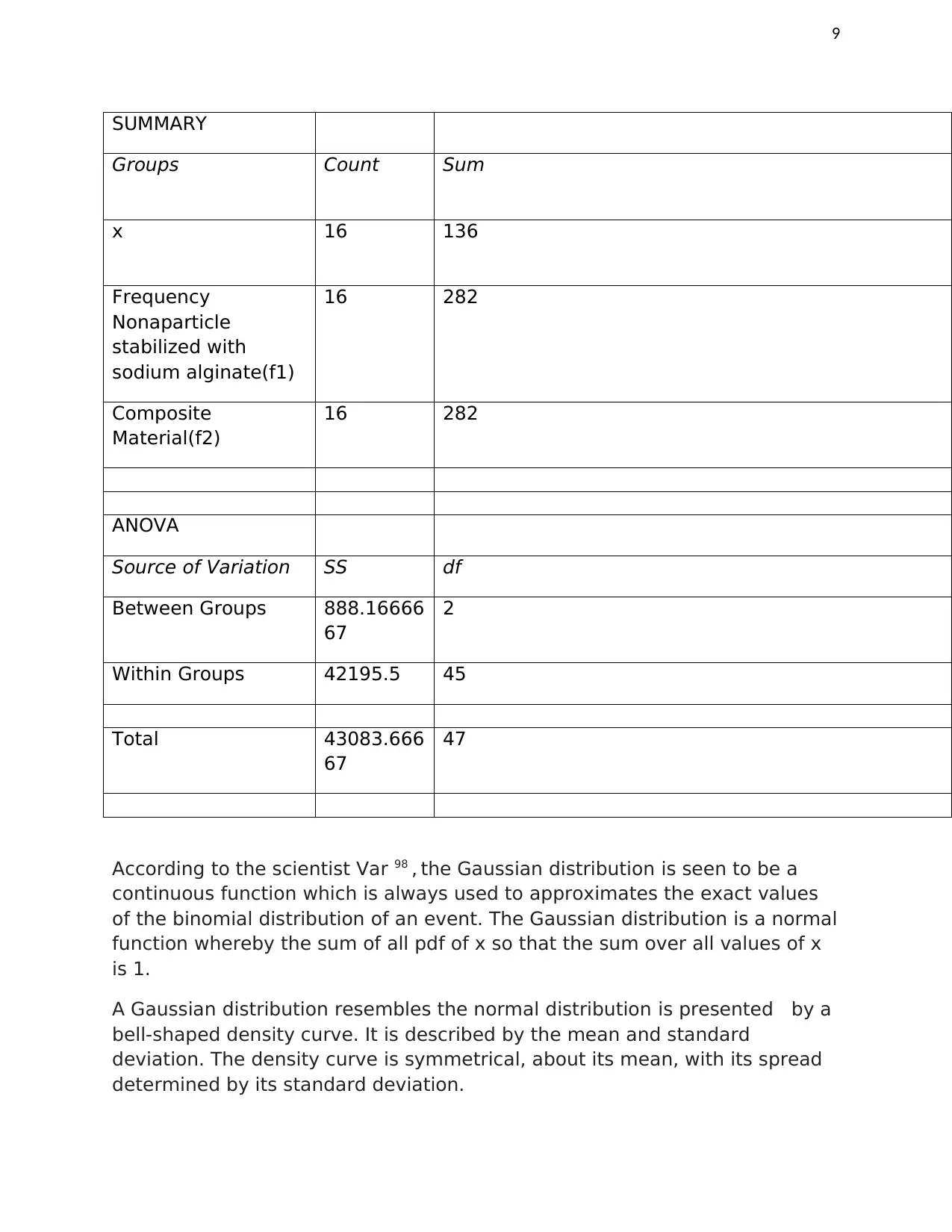
SUMMARY
Groups Count Sum
x 16 136
Frequency
Nonaparticle
stabilized with
sodium alginate(f1)
16 282
Composite
Material(f2)
16 282
ANOVA
Source of Variation SS df
Between Groups 888.16666
67
2
Within Groups 42195.5 45
Total 43083.666
67
47
According to the scientist Var 98 , the Gaussian distribution is seen to be a
continuous function which is always used to approximates the exact values
of the binomial distribution of an event. The Gaussian distribution is a normal
function whereby the sum of all pdf of x so that the sum over all values of x
is 1.
A Gaussian distribution resembles the normal distribution is presented by a
bell-shaped density curve. It is described by the mean and standard
deviation. The density curve is symmetrical, about its mean, with its spread
determined by its standard deviation.
SUMMARY
Groups Count Sum
x 16 136
Frequency
Nonaparticle
stabilized with
sodium alginate(f1)
16 282
Composite
Material(f2)
16 282
ANOVA
Source of Variation SS df
Between Groups 888.16666
67
2
Within Groups 42195.5 45
Total 43083.666
67
47
According to the scientist Var 98 , the Gaussian distribution is seen to be a
continuous function which is always used to approximates the exact values
of the binomial distribution of an event. The Gaussian distribution is a normal
function whereby the sum of all pdf of x so that the sum over all values of x
is 1.
A Gaussian distribution resembles the normal distribution is presented by a
bell-shaped density curve. It is described by the mean and standard
deviation. The density curve is symmetrical, about its mean, with its spread
determined by its standard deviation.
You're viewing a preview
Unlock full access by subscribing today!
10
The normal distribution is very vital in statistics because it fits many natural
conditions. The normal distribution is also function that explains how the
values of a variable are distributed, this is in refence to Var I98.
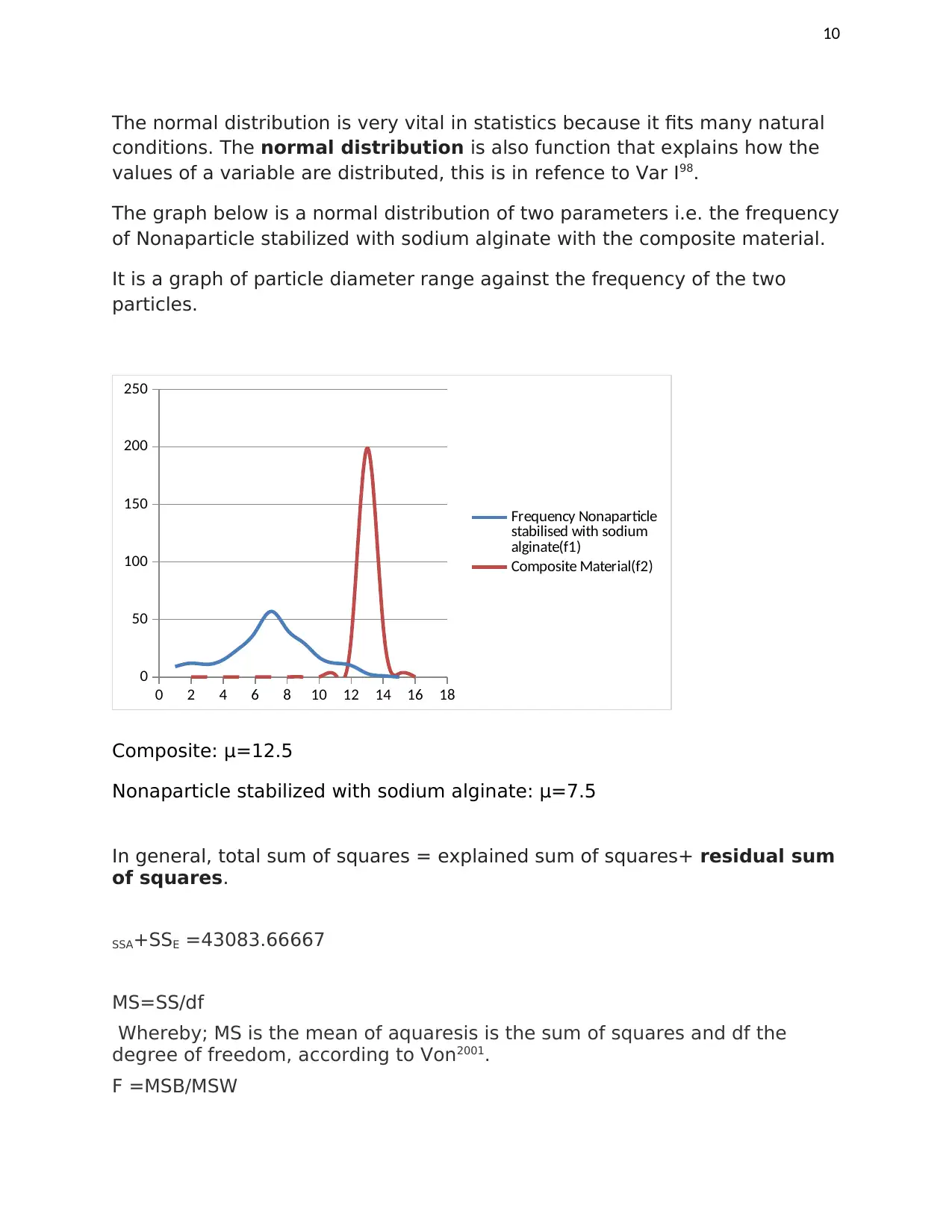
The graph below is a normal distribution of two parameters i.e. the frequency
of Nonaparticle stabilized with sodium alginate with the composite material.
It is a graph of particle diameter range against the frequency of the two
particles.
Composite: μ=12.5
Nonaparticle stabilized with sodium alginate: μ=7.5
In general, total sum of squares = explained sum of squares+ residual sum
of squares.
SSA+SSE =43083.66667
MS=SS/df
Whereby; MS is the mean of aquaresis is the sum of squares and df the
degree of freedom, according to Von2001.
F =MSB/MSW
0 2 4 6 8 10 12 14 16 18
0
50
100
150
200
250
Frequency Nonaparticle
stabilised with sodium
alginate(f1)
Composite Material(f2)
The normal distribution is very vital in statistics because it fits many natural
conditions. The normal distribution is also function that explains how the
values of a variable are distributed, this is in refence to Var I98.
The graph below is a normal distribution of two parameters i.e. the frequency
of Nonaparticle stabilized with sodium alginate with the composite material.
It is a graph of particle diameter range against the frequency of the two
particles.
Composite: μ=12.5
Nonaparticle stabilized with sodium alginate: μ=7.5
In general, total sum of squares = explained sum of squares+ residual sum
of squares.
SSA+SSE =43083.66667
MS=SS/df
Whereby; MS is the mean of aquaresis is the sum of squares and df the
degree of freedom, according to Von2001.
F =MSB/MSW
0 2 4 6 8 10 12 14 16 18
0
50
100
150
200
250
Frequency Nonaparticle
stabilised with sodium
alginate(f1)
Composite Material(f2)
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
11
Whereby MSB is the mean squares in between the groups.
MSW is the mean squares within the groups according to Montana Library1-5
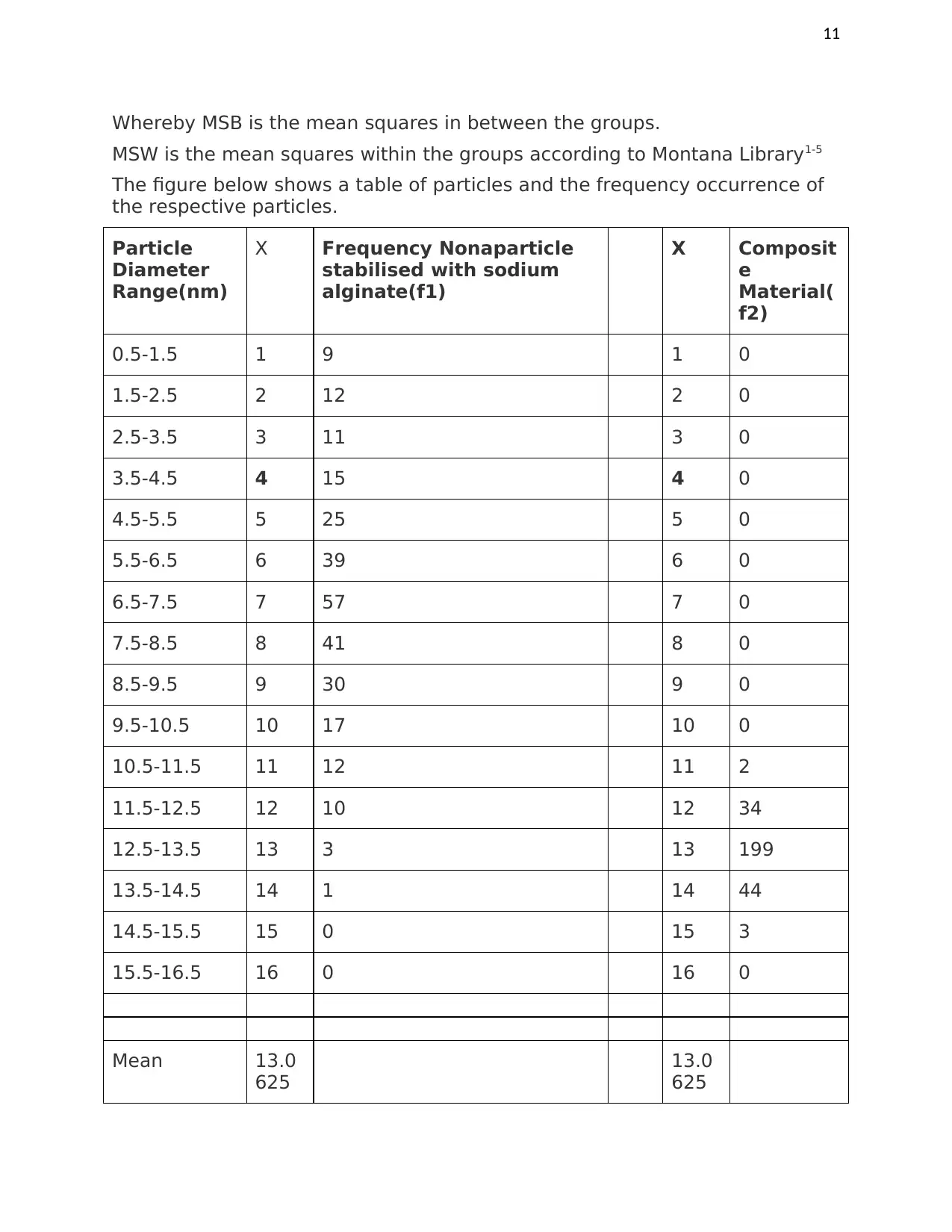
The figure below shows a table of particles and the frequency occurrence of
the respective particles.
Particle
Diameter
Range(nm)
X Frequency Nonaparticle
stabilised with sodium
alginate(f1)
X Composit
e
Material(
f2)
0.5-1.5 1 9 1 0
1.5-2.5 2 12 2 0
2.5-3.5 3 11 3 0
3.5-4.5 4 15 4 0
4.5-5.5 5 25 5 0
5.5-6.5 6 39 6 0
6.5-7.5 7 57 7 0
7.5-8.5 8 41 8 0
8.5-9.5 9 30 9 0
9.5-10.5 10 17 10 0
10.5-11.5 11 12 11 2
11.5-12.5 12 10 12 34
12.5-13.5 13 3 13 199
13.5-14.5 14 1 14 44
14.5-15.5 15 0 15 3
15.5-16.5 16 0 16 0
Mean 13.0
625
13.0
625
Whereby MSB is the mean squares in between the groups.
MSW is the mean squares within the groups according to Montana Library1-5
The figure below shows a table of particles and the frequency occurrence of
the respective particles.
Particle
Diameter
Range(nm)
X Frequency Nonaparticle
stabilised with sodium
alginate(f1)
X Composit
e
Material(
f2)
0.5-1.5 1 9 1 0
1.5-2.5 2 12 2 0
2.5-3.5 3 11 3 0
3.5-4.5 4 15 4 0
4.5-5.5 5 25 5 0
5.5-6.5 6 39 6 0
6.5-7.5 7 57 7 0
7.5-8.5 8 41 8 0
8.5-9.5 9 30 9 0
9.5-10.5 10 17 10 0
10.5-11.5 11 12 11 2
11.5-12.5 12 10 12 34
12.5-13.5 13 3 13 199
13.5-14.5 14 1 14 44
14.5-15.5 15 0 15 3
15.5-16.5 16 0 16 0
Mean 13.0
625
13.0
625

12
standard
deviation
12.8
5888
35.3
5163
The mean of both the nanoparticles are equal hence the from the test, the
Nonaparticles are statistically significant different.
However the standard deviations of the nonaparticles are different.
standard
deviation
12.8
5888
35.3
5163
The mean of both the nanoparticles are equal hence the from the test, the
Nonaparticles are statistically significant different.
However the standard deviations of the nonaparticles are different.
You're viewing a preview
Unlock full access by subscribing today!

13
References.
1. Manfroid J, Selman F, Jones H. Achieving 1% photometric accuracy with
the ESO Wide Field Imager. The Messenger. 2001.
2. Contreras MD, Díaz-Madrigal S, Pommerenke C. Fixed points and
boundary behaviour of the Koenigs function. InANNALES-ACADEMIAE
SCIENTIARUM FENNICAE MATHEMATICA 2004 Jan 1. ACADEMIA
SCIENTIARUM FENNICA.
3. Var I. Multivariate data analysis. vectors. 1998.
4. Clark V, Dunn OJ, Mickey RM. Applied statistics, analysis of variance
and regression. Wiley; 1974.
5. von Ende CN. Repeated-measures analysis. Design and analysis of
ecological experiments. 2001 Apr.
References.
1. Manfroid J, Selman F, Jones H. Achieving 1% photometric accuracy with
the ESO Wide Field Imager. The Messenger. 2001.
2. Contreras MD, Díaz-Madrigal S, Pommerenke C. Fixed points and
boundary behaviour of the Koenigs function. InANNALES-ACADEMIAE
SCIENTIARUM FENNICAE MATHEMATICA 2004 Jan 1. ACADEMIA
SCIENTIARUM FENNICA.
3. Var I. Multivariate data analysis. vectors. 1998.
4. Clark V, Dunn OJ, Mickey RM. Applied statistics, analysis of variance
and regression. Wiley; 1974.
5. von Ende CN. Repeated-measures analysis. Design and analysis of
ecological experiments. 2001 Apr.
1 out of 13
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.