FIN510 - Corporate Finance: Investment and Risk Analysis Assignment
VerifiedAdded on 2022/12/27
|11
|3015
|25
Homework Assignment
AI Summary
This assignment solution for FIN510, a Corporate Finance course, analyzes monthly returns, average returns, and volatility of five selected companies and a market index (ASX200). It calculates standard deviations, betas, and provides a risk evaluation report for clients, including recommendations for investment strategies and portfolio development. The solution includes detailed calculations of monthly returns, average returns, variance, standard deviation, and beta for each company, along with portfolio analysis. The report assesses risk, analyzes whether shares are over or underpriced, and suggests investment recommendations. The assignment covers key concepts in corporate finance such as portfolio management, risk assessment, and investment strategy, and the solution is presented in an organized, easy-to-understand format, including relevant formulas, and excel outputs.

1
FIN510Aspects of Corporate Finance
Written Assignment
FIN510Aspects of Corporate Finance
Written Assignment
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

2
Contents
Solution to Part 1: Monthly and average returns of shares and portfolio........................................3
Sub-Section A: Estimation of average of monthly returns on the basis of monthly returns
computed above in respect of each share and market index ASX200.............................................5
Sub-Section B: Calculation of average return of the portfolio (Portfolio is made of equal weight
of each of five shares)......................................................................................................................5
Solution to Part 2: Volatility............................................................................................................6
Sub Section A: Standard deviation of returns of five companies....................................................6
Sub Section B: Standard Deviation of Portfolio and its comparison with each of individual share
.........................................................................................................................................................7
Sub Section C: Standard Deviation of ASX200 and its comparison...............................................7
Solution to Part 3: Beta Calculation................................................................................................8
Sub Section A: Beta of each company (Share)................................................................................8
Sub Section B: Analysis of beta for each company.........................................................................8
Solution to Part 4: Forecast & Investment strategy.........................................................................9
Sub Section A: Report presented to the clients of Tri-Star Management........................................9
Part a: Risk evaluation of each company.....................................................................................9
Part b: Analysis of whether shares are overpriced, underpriced, or correctly price during the
forecasted period..........................................................................................................................9
Part c: Recommendation for investment in each of the investment...........................................10
Sub Section B: Recommendation to invest in portfolio................................................................10
Contents
Solution to Part 1: Monthly and average returns of shares and portfolio........................................3
Sub-Section A: Estimation of average of monthly returns on the basis of monthly returns
computed above in respect of each share and market index ASX200.............................................5
Sub-Section B: Calculation of average return of the portfolio (Portfolio is made of equal weight
of each of five shares)......................................................................................................................5
Solution to Part 2: Volatility............................................................................................................6
Sub Section A: Standard deviation of returns of five companies....................................................6
Sub Section B: Standard Deviation of Portfolio and its comparison with each of individual share
.........................................................................................................................................................7
Sub Section C: Standard Deviation of ASX200 and its comparison...............................................7
Solution to Part 3: Beta Calculation................................................................................................8
Sub Section A: Beta of each company (Share)................................................................................8
Sub Section B: Analysis of beta for each company.........................................................................8
Solution to Part 4: Forecast & Investment strategy.........................................................................9
Sub Section A: Report presented to the clients of Tri-Star Management........................................9
Part a: Risk evaluation of each company.....................................................................................9
Part b: Analysis of whether shares are overpriced, underpriced, or correctly price during the
forecasted period..........................................................................................................................9
Part c: Recommendation for investment in each of the investment...........................................10
Sub Section B: Recommendation to invest in portfolio................................................................10
3
Solution to Part 1: Monthly and average returns of shares and portfolio
In this section there is required to estimate the monthly return and average of monthly
return of all the stocks (Shares) and market index (ASX200) for the given data in excel sheet.
The five shares or stocks selected for this purpose are given as:
Code Company Name Sector
AMP.AX ($A) AMP Limited Banking Sector
ANZ.AX ($A) Australia and New Zealand Banking
Group Limited Banking Sector
CBA.AX ($A) Commonwealth Bank of Australia Banking Sector
NAB.AX($A) National Australia Bank Limited Banking Sector
QAN.AX ($A) Qantas Airways Limited Airline Sector
In order to compute the monthly return there is need to apply the formula as given below:
Returnt = Pt −Pt−1
Pt−1
×100 , (Levy, 2011)
In the above formula, Pt refers to share price of current month and Pt-1 means share price
of previous month of the same stock for which calculation has been made. While making the
calculation it is important to note that result arise in number format in excel but it is required to
convert it in percentage format in order to have better understandability. It is reason why
monthly returns have been multiplied with 100 in above formula.
Meaning of monthly return: Monthly return on share means percentage of return or income
received by the investor or generated by respective share in the month time. In other words it
tells percentage return that investor will earn if funds are invested for particular month. It is very
useful for investors or market analyst to judge the movement in share price of particular stock.
Through the application of above formula, monthly return of each stock and market index
has been computed in the given excel and same has been presented below:
Date ASX200
AMP.AX
($A)
ANZ.A
X ($A)
CBA.AX
($A)
NAB.AX($A
)
QAN.A
X ($A)
Portfolio
(equal
weight)
Jan-15
Feb-15 -0.63 -3.88 3.68 3.82 1.71 7.96 2.66
Mar-
15 -1.72 2.07 -7.23 -4.85 -4.62 8.65 -1.19
Apr-15 -0.22 3.42 -2.35 -4.25 -5.33 3.83 -0.94
Solution to Part 1: Monthly and average returns of shares and portfolio
In this section there is required to estimate the monthly return and average of monthly
return of all the stocks (Shares) and market index (ASX200) for the given data in excel sheet.
The five shares or stocks selected for this purpose are given as:
Code Company Name Sector
AMP.AX ($A) AMP Limited Banking Sector
ANZ.AX ($A) Australia and New Zealand Banking
Group Limited Banking Sector
CBA.AX ($A) Commonwealth Bank of Australia Banking Sector
NAB.AX($A) National Australia Bank Limited Banking Sector
QAN.AX ($A) Qantas Airways Limited Airline Sector
In order to compute the monthly return there is need to apply the formula as given below:
Returnt = Pt −Pt−1
Pt−1
×100 , (Levy, 2011)
In the above formula, Pt refers to share price of current month and Pt-1 means share price
of previous month of the same stock for which calculation has been made. While making the
calculation it is important to note that result arise in number format in excel but it is required to
convert it in percentage format in order to have better understandability. It is reason why
monthly returns have been multiplied with 100 in above formula.
Meaning of monthly return: Monthly return on share means percentage of return or income
received by the investor or generated by respective share in the month time. In other words it
tells percentage return that investor will earn if funds are invested for particular month. It is very
useful for investors or market analyst to judge the movement in share price of particular stock.
Through the application of above formula, monthly return of each stock and market index
has been computed in the given excel and same has been presented below:
Date ASX200
AMP.AX
($A)
ANZ.A
X ($A)
CBA.AX
($A)
NAB.AX($A
)
QAN.A
X ($A)
Portfolio
(equal
weight)
Jan-15
Feb-15 -0.63 -3.88 3.68 3.82 1.71 7.96 2.66
Mar-
15 -1.72 2.07 -7.23 -4.85 -4.62 8.65 -1.19
Apr-15 -0.22 3.42 -2.35 -4.25 -5.33 3.83 -0.94
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

4
May-
15 -5.51 -9.61 -0.39 0.05 -0.05 -10.23 -4.05
Jun-15 4.40 9.80 1.49 2.85 4.38 18.67 7.44
Jul-15 -8.64 -9.98 -14.53 -12.32 -10.35 -10.40 -11.52
Aug-
15
-3.56 -6.55 -3.04 -2.09 -3.82 10.71 -0.96
Sep-15 4.34 5.54 0.48 5.51 0.57 -0.29 2.36
Oct-15 -1.39 1.40 -0.22 3.52 -2.52 -7.85 -1.13
Nov-
15
2.50 0.34 6.68 7.68 6.41 12.36 6.69
Dec-15 -5.48 -7.89 -13.43 -8.02 -8.41 -5.13 -8.58
Jan-16 -2.49 -0.93 -7.36 -10.84 -9.36 -0.52 -5.80
Feb-16 4.14 8.83 4.73 9.74 8.47 5.44 7.44
Mar-
16 3.33 4.30 3.45 -1.37 3.62 -20.88 -2.18
Apr-16 2.41 -4.08 4.99 4.79 -0.15 -4.35 0.24
May-
16 -2.70 -8.51 -2.23 -3.95 -3.03 -8.44 -5.23
Jun-16 6.28 12.60 7.13 4.01 4.36 12.06 8.03
Jul-16 -2.32 -9.47 4.10 -7.16 3.01 2.53 -1.40
Aug-
16 0.05 3.04 2.71 3.86 1.94 -3.70 1.57
Sep-16 -2.17 -13.45 0.80 1.37 0.47 0.14 -2.13
Oct-16 2.31 2.84 2.01 7.17 3.32 7.84 4.64
Nov-
16 4.14 7.23 10.19 4.78 6.49 0.91 5.92
Dec-16 -0.79 -0.79 -3.71 -0.91 2.12 2.40 -0.18
Jan-17 1.62 -2.40 5.50 0.81 5.47 9.97 3.87
Feb-17 2.67 9.16 2.98 6.83 4.22 3.73 5.38
Mar-
17 1.01 3.47 2.95 1.73 1.98 11.07 4.24
Apr-17 -3.37 -5.78 -14.50 -8.87 -11.41 18.16 -4.48
May-
17 -0.05 2.77 5.28 3.97 1.31 14.17 5.50
Jun-17 -0.02 3.85 3.17 1.11 1.22 -6.99 0.47
Jul-17 -0.11 -5.38 -0.78 -9.47 0.83 7.52 -1.45
Aug-
17 -0.58 -2.53 0.68 2.17 4.30 1.92 1.31
Sep-17 4.00 2.90 1.08 3.16 3.68 6.81 3.53
Oct-17 1.03 2.82 -4.88 2.32 -9.40 -7.80 -3.39
Nov-
17 1.59 1.57 3.72 1.15 3.16 -11.11 -0.30
Dec-17 -0.45 1.16 -0.56 -1.83 -1.49 4.56 0.37
May-
15 -5.51 -9.61 -0.39 0.05 -0.05 -10.23 -4.05
Jun-15 4.40 9.80 1.49 2.85 4.38 18.67 7.44
Jul-15 -8.64 -9.98 -14.53 -12.32 -10.35 -10.40 -11.52
Aug-
15
-3.56 -6.55 -3.04 -2.09 -3.82 10.71 -0.96
Sep-15 4.34 5.54 0.48 5.51 0.57 -0.29 2.36
Oct-15 -1.39 1.40 -0.22 3.52 -2.52 -7.85 -1.13
Nov-
15
2.50 0.34 6.68 7.68 6.41 12.36 6.69
Dec-15 -5.48 -7.89 -13.43 -8.02 -8.41 -5.13 -8.58
Jan-16 -2.49 -0.93 -7.36 -10.84 -9.36 -0.52 -5.80
Feb-16 4.14 8.83 4.73 9.74 8.47 5.44 7.44
Mar-
16 3.33 4.30 3.45 -1.37 3.62 -20.88 -2.18
Apr-16 2.41 -4.08 4.99 4.79 -0.15 -4.35 0.24
May-
16 -2.70 -8.51 -2.23 -3.95 -3.03 -8.44 -5.23
Jun-16 6.28 12.60 7.13 4.01 4.36 12.06 8.03
Jul-16 -2.32 -9.47 4.10 -7.16 3.01 2.53 -1.40
Aug-
16 0.05 3.04 2.71 3.86 1.94 -3.70 1.57
Sep-16 -2.17 -13.45 0.80 1.37 0.47 0.14 -2.13
Oct-16 2.31 2.84 2.01 7.17 3.32 7.84 4.64
Nov-
16 4.14 7.23 10.19 4.78 6.49 0.91 5.92
Dec-16 -0.79 -0.79 -3.71 -0.91 2.12 2.40 -0.18
Jan-17 1.62 -2.40 5.50 0.81 5.47 9.97 3.87
Feb-17 2.67 9.16 2.98 6.83 4.22 3.73 5.38
Mar-
17 1.01 3.47 2.95 1.73 1.98 11.07 4.24
Apr-17 -3.37 -5.78 -14.50 -8.87 -11.41 18.16 -4.48
May-
17 -0.05 2.77 5.28 3.97 1.31 14.17 5.50
Jun-17 -0.02 3.85 3.17 1.11 1.22 -6.99 0.47
Jul-17 -0.11 -5.38 -0.78 -9.47 0.83 7.52 -1.45
Aug-
17 -0.58 -2.53 0.68 2.17 4.30 1.92 1.31
Sep-17 4.00 2.90 1.08 3.16 3.68 6.81 3.53
Oct-17 1.03 2.82 -4.88 2.32 -9.40 -7.80 -3.39
Nov-
17 1.59 1.57 3.72 1.15 3.16 -11.11 -0.30
Dec-17 -0.45 1.16 -0.56 -1.83 -1.49 4.56 0.37
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

5
In the above table, monthly returns of all five shares and ASX200 have been shown form
Feb-15 to Dec-17. It is not possible to calculate the monthly return for month Jan-15 due to share
price of previous month has not been provided.
Sub-Section A: Estimation of average of monthly returns on the basis of monthly returns
computed above in respect of each share and market index ASX200
In order to estimate the average of monthly return it is required to divide the sum of
monthly returns with number of months. Same can be computed through using the excel formula
known as “Average” (Madura, 2014).
Average of monthly returns of each share and market index has been computed through
using the excel formula and answer derived has been presented below:
Particulars ASX200 AMP.AX
($A)
ANZ.AX
($A)
CBA.AX
($A) NAB.AX($A) QAN.AX
($A)
Average
Monthly
return or
Mean
0.10 -0.06 0.07 0.18 0.09 2.11
The average return means return earned on the particular share by the investor if money
has been invested for particular months and return has been made out monthly basis. Returns are
first calculated on monthly basis and then their average is made to predict the average monthly
return.
On comparison of average monthly return of each stock with the market index ASX200 it
has been found that AMP Limited, NAB Bank & ANZ Bank have average return below the
average monthly return of market index ASX200 and average monthly return of Qantas Airways
& Commonwealth Bank were greater than market index ASX200. It means Qantas Airways and
Commonwealth Bank have performed well with respect to the market as they have earned higher
return as compared to market return. But it is highly important to analyse the stock with their risk
factor (Volatility) in order to judge the performance of each stock with respect to their market.
Sub-Section B: Calculation of average return of the portfolio (Portfolio is made of equal
weight of each of five shares)
It is important to understand what is meant by portfolio. Portfolio represents group of
financial assets such as stocks, commodities, bonds, currencies and cash equivalents. The
purpose of portfolio is to lower the risk of investment in the stocks and increase the overall
return. Portfolio is for those investors who are risk adverse but want reasonable return on their
investment.
In the above table, monthly returns of all five shares and ASX200 have been shown form
Feb-15 to Dec-17. It is not possible to calculate the monthly return for month Jan-15 due to share
price of previous month has not been provided.
Sub-Section A: Estimation of average of monthly returns on the basis of monthly returns
computed above in respect of each share and market index ASX200
In order to estimate the average of monthly return it is required to divide the sum of
monthly returns with number of months. Same can be computed through using the excel formula
known as “Average” (Madura, 2014).
Average of monthly returns of each share and market index has been computed through
using the excel formula and answer derived has been presented below:
Particulars ASX200 AMP.AX
($A)
ANZ.AX
($A)
CBA.AX
($A) NAB.AX($A) QAN.AX
($A)
Average
Monthly
return or
Mean
0.10 -0.06 0.07 0.18 0.09 2.11
The average return means return earned on the particular share by the investor if money
has been invested for particular months and return has been made out monthly basis. Returns are
first calculated on monthly basis and then their average is made to predict the average monthly
return.
On comparison of average monthly return of each stock with the market index ASX200 it
has been found that AMP Limited, NAB Bank & ANZ Bank have average return below the
average monthly return of market index ASX200 and average monthly return of Qantas Airways
& Commonwealth Bank were greater than market index ASX200. It means Qantas Airways and
Commonwealth Bank have performed well with respect to the market as they have earned higher
return as compared to market return. But it is highly important to analyse the stock with their risk
factor (Volatility) in order to judge the performance of each stock with respect to their market.
Sub-Section B: Calculation of average return of the portfolio (Portfolio is made of equal
weight of each of five shares)
It is important to understand what is meant by portfolio. Portfolio represents group of
financial assets such as stocks, commodities, bonds, currencies and cash equivalents. The
purpose of portfolio is to lower the risk of investment in the stocks and increase the overall
return. Portfolio is for those investors who are risk adverse but want reasonable return on their
investment.

6
In the given case, portfolio has been developed that comprises five shares (stocks) in
equal quantity. It means each share will have weight of 0.20 or 20% (100/5). It can be
understood as if investor wants to invest $1 million than as per portfolio, $200000 will be
invested in each of AMP Limited share, ANZ Bank, CBA Bank, NAB Bank and Qantas Airways
(Moles and Kidwekk, 2011).
To calculate the average of monthly return of portfolio there is first need to estimate the
monthly return of portfolio that comprise of AMP Limited share, ANZ Bank, CBA Bank, NAB
Bank and Qantas Airways in equal quantity. Monthly return of portfolio can be estimated
through use of following formula:
Monthly return of given portfolio: (0.20*monthly return of AMP Limited) + (0.20*monthly
return of ANZ Bank) + (0.20*monthly return of Commonwealth bank) + (0.20*monthly return
of NAB Bank) + (0.20*monthly return of Qantas Airways)
Note: Monthly returns of portfolio can be seen from the first table presented in this report.
Average of monthly return of portfolio will computed simply by calculating the mean of
all the monthly returns and it can be also be computed the excel formula “Average”. The average
of monthly return of portfolio is 0.479% (Reilly and Brown, 2011).
Solution to Part 2: Volatility
Sub Section A: Standard deviation of returns of five companies
Standard deviation refers to the statistic measurement of dispersion of data from its mean
and it is estimated as the square root of variance. In context of securities returns, standard
deviation provides level of dispersion of monthly returns with respect to its mean (Average).
Standard deviation helps to make understand the how volatile the return are as compared to their
average. More the volatility is more will the risk and vice versa. So, if standard deviation is high
it indicates the highly risk stock and if standard deviation is low if reflects least risk stock.
Standard deviation measures the total risk of the stock (Systematic and Unsystematic risk).
Formula of Standard Deviation is = Square root of Variance
Variance can be calculated as:
Particulars ASX20
0
AMP.A
X ($A)
ANZ.A
X ($A)
CBA.A
X ($A)
NAB.AX($
A)
QAN.A
X ($A)
Portfolio (equal
weight)
In the given case, portfolio has been developed that comprises five shares (stocks) in
equal quantity. It means each share will have weight of 0.20 or 20% (100/5). It can be
understood as if investor wants to invest $1 million than as per portfolio, $200000 will be
invested in each of AMP Limited share, ANZ Bank, CBA Bank, NAB Bank and Qantas Airways
(Moles and Kidwekk, 2011).
To calculate the average of monthly return of portfolio there is first need to estimate the
monthly return of portfolio that comprise of AMP Limited share, ANZ Bank, CBA Bank, NAB
Bank and Qantas Airways in equal quantity. Monthly return of portfolio can be estimated
through use of following formula:
Monthly return of given portfolio: (0.20*monthly return of AMP Limited) + (0.20*monthly
return of ANZ Bank) + (0.20*monthly return of Commonwealth bank) + (0.20*monthly return
of NAB Bank) + (0.20*monthly return of Qantas Airways)
Note: Monthly returns of portfolio can be seen from the first table presented in this report.
Average of monthly return of portfolio will computed simply by calculating the mean of
all the monthly returns and it can be also be computed the excel formula “Average”. The average
of monthly return of portfolio is 0.479% (Reilly and Brown, 2011).
Solution to Part 2: Volatility
Sub Section A: Standard deviation of returns of five companies
Standard deviation refers to the statistic measurement of dispersion of data from its mean
and it is estimated as the square root of variance. In context of securities returns, standard
deviation provides level of dispersion of monthly returns with respect to its mean (Average).
Standard deviation helps to make understand the how volatile the return are as compared to their
average. More the volatility is more will the risk and vice versa. So, if standard deviation is high
it indicates the highly risk stock and if standard deviation is low if reflects least risk stock.
Standard deviation measures the total risk of the stock (Systematic and Unsystematic risk).
Formula of Standard Deviation is = Square root of Variance
Variance can be calculated as:
Particulars ASX20
0
AMP.A
X ($A)
ANZ.A
X ($A)
CBA.A
X ($A)
NAB.AX($
A)
QAN.A
X ($A)
Portfolio (equal
weight)
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

7
Mean 0.10 -0.06 0.07 0.18 0.09 2.11 0.479
Variance 10.578 39.882 34.443 31.113 26.524 83.286 21.286
Standard
Deviation 3.252 6.315 5.869 5.578 5.150 9.126 4.614
Standard deviation of all the five shares have been shown in above table and looking at
them it can be predicted that Qantas Airways is highly volatile stock and NAB Bank is least
volatile among all the five shares.
Sub Section B: Standard Deviation of Portfolio and its comparison with each of individual
share
The standard deviation of portfolio has been calculated and it is 4.614, which is least as
compared to standard deviation of all the stocks. It means monthly return of portfolio is least
volatile as compared to individual stock, representing the less risky investment form the point of
investor.
Sub Section C: Standard Deviation of ASX200 and its comparison
Standard deviation of ASX200 (Market Index) is 3.252 which is very less as compared to
portfolio and all shares standard deviation. It means monthly returns of market are less volatile
and keep close to the mean. Overall it can be said that high volatility of shares are mainly due to
internal factors or unsystematic risk as it cannot be avoided. It is necessary to estimate the beta
factor to have knowledge of systematic risk (Sharifzadeh, 2010).
Mean 0.10 -0.06 0.07 0.18 0.09 2.11 0.479
Variance 10.578 39.882 34.443 31.113 26.524 83.286 21.286
Standard
Deviation 3.252 6.315 5.869 5.578 5.150 9.126 4.614
Standard deviation of all the five shares have been shown in above table and looking at
them it can be predicted that Qantas Airways is highly volatile stock and NAB Bank is least
volatile among all the five shares.
Sub Section B: Standard Deviation of Portfolio and its comparison with each of individual
share
The standard deviation of portfolio has been calculated and it is 4.614, which is least as
compared to standard deviation of all the stocks. It means monthly return of portfolio is least
volatile as compared to individual stock, representing the less risky investment form the point of
investor.
Sub Section C: Standard Deviation of ASX200 and its comparison
Standard deviation of ASX200 (Market Index) is 3.252 which is very less as compared to
portfolio and all shares standard deviation. It means monthly returns of market are less volatile
and keep close to the mean. Overall it can be said that high volatility of shares are mainly due to
internal factors or unsystematic risk as it cannot be avoided. It is necessary to estimate the beta
factor to have knowledge of systematic risk (Sharifzadeh, 2010).
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
8
Solution to Part 3: Beta Calculation
Sub Section A: Beta of each company (Share)
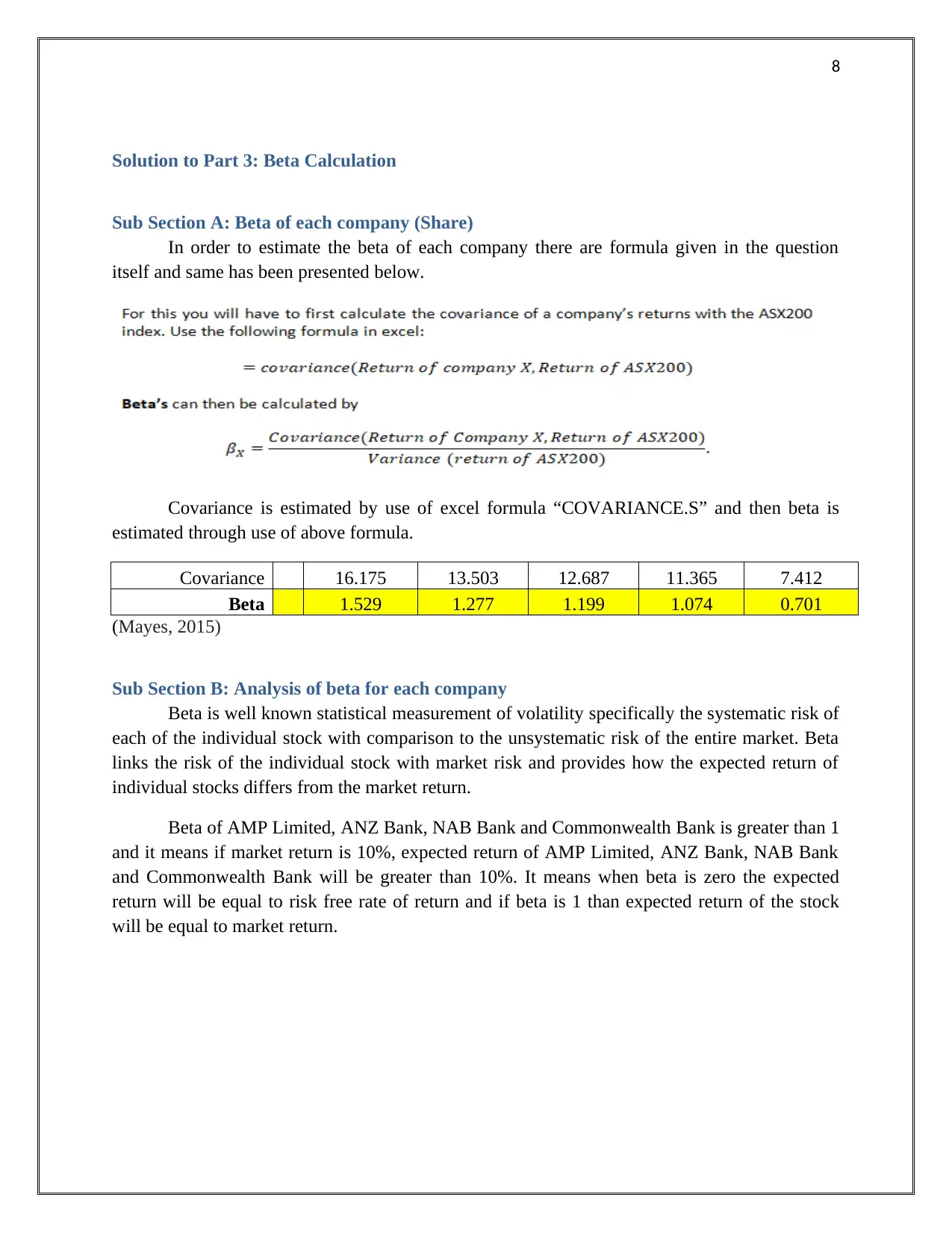
In order to estimate the beta of each company there are formula given in the question
itself and same has been presented below.
Covariance is estimated by use of excel formula “COVARIANCE.S” and then beta is
estimated through use of above formula.
Covariance 16.175 13.503 12.687 11.365 7.412
Beta 1.529 1.277 1.199 1.074 0.701
(Mayes, 2015)
Sub Section B: Analysis of beta for each company
Beta is well known statistical measurement of volatility specifically the systematic risk of
each of the individual stock with comparison to the unsystematic risk of the entire market. Beta
links the risk of the individual stock with market risk and provides how the expected return of
individual stocks differs from the market return.
Beta of AMP Limited, ANZ Bank, NAB Bank and Commonwealth Bank is greater than 1
and it means if market return is 10%, expected return of AMP Limited, ANZ Bank, NAB Bank
and Commonwealth Bank will be greater than 10%. It means when beta is zero the expected
return will be equal to risk free rate of return and if beta is 1 than expected return of the stock
will be equal to market return.
Solution to Part 3: Beta Calculation
Sub Section A: Beta of each company (Share)
In order to estimate the beta of each company there are formula given in the question
itself and same has been presented below.
Covariance is estimated by use of excel formula “COVARIANCE.S” and then beta is
estimated through use of above formula.
Covariance 16.175 13.503 12.687 11.365 7.412
Beta 1.529 1.277 1.199 1.074 0.701
(Mayes, 2015)
Sub Section B: Analysis of beta for each company
Beta is well known statistical measurement of volatility specifically the systematic risk of
each of the individual stock with comparison to the unsystematic risk of the entire market. Beta
links the risk of the individual stock with market risk and provides how the expected return of
individual stocks differs from the market return.
Beta of AMP Limited, ANZ Bank, NAB Bank and Commonwealth Bank is greater than 1
and it means if market return is 10%, expected return of AMP Limited, ANZ Bank, NAB Bank
and Commonwealth Bank will be greater than 10%. It means when beta is zero the expected
return will be equal to risk free rate of return and if beta is 1 than expected return of the stock
will be equal to market return.
9
Solution to Part 4: Forecast & Investment strategy
Sub Section A: Report presented to the clients of Tri-Star Management
Part a: Risk evaluation of each company
The proposal of Tri Star Management is to examine the share price of the five selected
company stocks. There are five company stocks selected for the purpose out of which four
belong to the banking sector and one operates within the airline sector. The four banking
company stock selected for examination purpose are ANZ bank, AMP Limited, NAB Bank and
Commonwealth Bank while Qantas airline belongs to the airline sector. As such, it can be said
that all the four banks stocks will face similar type of external risks as they operate in the
Australian banking sector while Qantas operates in airline sector of the country and thus will
come across different type of external risks. The risk assessment in relation to each of the
selected stocks can be done primarily with the use of examining the market volatility, that is, by
measuring the beta factor for each of the five selected stocks. The best factor of each company
has been depicted in the above table and all the banking stocks have beta value higher than 1
while that f Qantas airline lies below the value of 1. It infers that the stocks of the banking
companies are associated with higher risk in comparison to that of Airline Company. The
average return realized from the selected banking stocks on average basis is significantly less in
comparison to the Qantas Airlines. The estimated monthly average return for each stock as per
the forecasted period has been depicted below:
Particulars ASX200 AMP.AX
($A)
ANZ.AX
($A)
CBA.AX
($A)
NAB.AX($A
)
QAN.AX
($A)
Expected
return
(monthly) 0.52 -5.05 0.87 -0.35 0.05 4.84
Thus, it can be said on the basis of the above table that Qantas airline is associated with
having higher return and lesser risk, that is, lower beta among all the selected stocks. Thus, it can
be said on the basis of risk and return analysis that the best stock for investing is Qantas Airways
followed by ANZ bank (Reilly and Brown, 2011).
Part b: Analysis of whether shares are overpriced, underpriced, or correctly price during
the forecasted period
Capital asset pricing model can be used to evaluate whether stock is overpriced,
underpriced, or correctly price. When CAPM return (expected return) is more than the forecast
return of each of individual stock then in that case stock is overpriced and vice-versa. When both
CAPM return and forecast return is equal than stock is correctly priced.
Solution to Part 4: Forecast & Investment strategy
Sub Section A: Report presented to the clients of Tri-Star Management
Part a: Risk evaluation of each company
The proposal of Tri Star Management is to examine the share price of the five selected
company stocks. There are five company stocks selected for the purpose out of which four
belong to the banking sector and one operates within the airline sector. The four banking
company stock selected for examination purpose are ANZ bank, AMP Limited, NAB Bank and
Commonwealth Bank while Qantas airline belongs to the airline sector. As such, it can be said
that all the four banks stocks will face similar type of external risks as they operate in the
Australian banking sector while Qantas operates in airline sector of the country and thus will
come across different type of external risks. The risk assessment in relation to each of the
selected stocks can be done primarily with the use of examining the market volatility, that is, by
measuring the beta factor for each of the five selected stocks. The best factor of each company
has been depicted in the above table and all the banking stocks have beta value higher than 1
while that f Qantas airline lies below the value of 1. It infers that the stocks of the banking
companies are associated with higher risk in comparison to that of Airline Company. The
average return realized from the selected banking stocks on average basis is significantly less in
comparison to the Qantas Airlines. The estimated monthly average return for each stock as per
the forecasted period has been depicted below:
Particulars ASX200 AMP.AX
($A)
ANZ.AX
($A)
CBA.AX
($A)
NAB.AX($A
)
QAN.AX
($A)
Expected
return
(monthly) 0.52 -5.05 0.87 -0.35 0.05 4.84
Thus, it can be said on the basis of the above table that Qantas airline is associated with
having higher return and lesser risk, that is, lower beta among all the selected stocks. Thus, it can
be said on the basis of risk and return analysis that the best stock for investing is Qantas Airways
followed by ANZ bank (Reilly and Brown, 2011).
Part b: Analysis of whether shares are overpriced, underpriced, or correctly price during
the forecasted period
Capital asset pricing model can be used to evaluate whether stock is overpriced,
underpriced, or correctly price. When CAPM return (expected return) is more than the forecast
return of each of individual stock then in that case stock is overpriced and vice-versa. When both
CAPM return and forecast return is equal than stock is correctly priced.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

10
Below table reflects expected return calculated using CAPM formula and forecast return
of each of individual stock. Then using these rates analysis of individual stock is made to tell
whether stock is underpriced, overpriced or correctly priced (Sharifzadeh, 2010).
Expected return (monthly)
Forecasted -5.05 0.87 -0.35 0.05 4.84
Required return (CAPM) 0.74 0.63 0.60 0.55 0.40
Analysis
Overprice
d
Underprice
d
Overprice
d
Overprice
d
Underprice
d
Part c: Recommendation for investment in each of the investment
It is highly recommended to choose Qantas Airways for investment purpose as it has very
return and lowest beta as compared to all the companies under review.
Sub Section B: Recommendation to invest in portfolio
As per understanding of risk and return concept, the Weightage of portfolio is not
properly managed as current portfolio has low return and high risk as compared to individual
stocks. So it not recommended making invest in portfolio.
Below table reflects expected return calculated using CAPM formula and forecast return
of each of individual stock. Then using these rates analysis of individual stock is made to tell
whether stock is underpriced, overpriced or correctly priced (Sharifzadeh, 2010).
Expected return (monthly)
Forecasted -5.05 0.87 -0.35 0.05 4.84
Required return (CAPM) 0.74 0.63 0.60 0.55 0.40
Analysis
Overprice
d
Underprice
d
Overprice
d
Overprice
d
Underprice
d
Part c: Recommendation for investment in each of the investment
It is highly recommended to choose Qantas Airways for investment purpose as it has very
return and lowest beta as compared to all the companies under review.
Sub Section B: Recommendation to invest in portfolio
As per understanding of risk and return concept, the Weightage of portfolio is not
properly managed as current portfolio has low return and high risk as compared to individual
stocks. So it not recommended making invest in portfolio.
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

11
References
Levy, H. 2011. The Capital Asset Pricing Model in the 21st Century: Analytical, Empirical, and
Behavioral Perspectives. USA: Cambridge University Press.
Madura, J. 2014. Financial Markets and Institutions. Germany: Cengage Learning.
Mayes, TR 2015, Financial Analysis with Microsoft Excel. Boston: Cengage Learning.
Moles, P. and Kidwekk, D. 2011. Corporate finance. USA: John Wiley &sons.
Reilly.F.K. and Brown.K.C. 2011. Investment analysis & portfolio management. Australia:
South western Cengage learning.
Sharifzadeh, M. 2010. An Empirical and Theoretical Analysis of Capital Asset Pricing Model.
USA: John Wiley &sons.
References
Levy, H. 2011. The Capital Asset Pricing Model in the 21st Century: Analytical, Empirical, and
Behavioral Perspectives. USA: Cambridge University Press.
Madura, J. 2014. Financial Markets and Institutions. Germany: Cengage Learning.
Mayes, TR 2015, Financial Analysis with Microsoft Excel. Boston: Cengage Learning.
Moles, P. and Kidwekk, D. 2011. Corporate finance. USA: John Wiley &sons.
Reilly.F.K. and Brown.K.C. 2011. Investment analysis & portfolio management. Australia:
South western Cengage learning.
Sharifzadeh, M. 2010. An Empirical and Theoretical Analysis of Capital Asset Pricing Model.
USA: John Wiley &sons.
1 out of 11
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.





