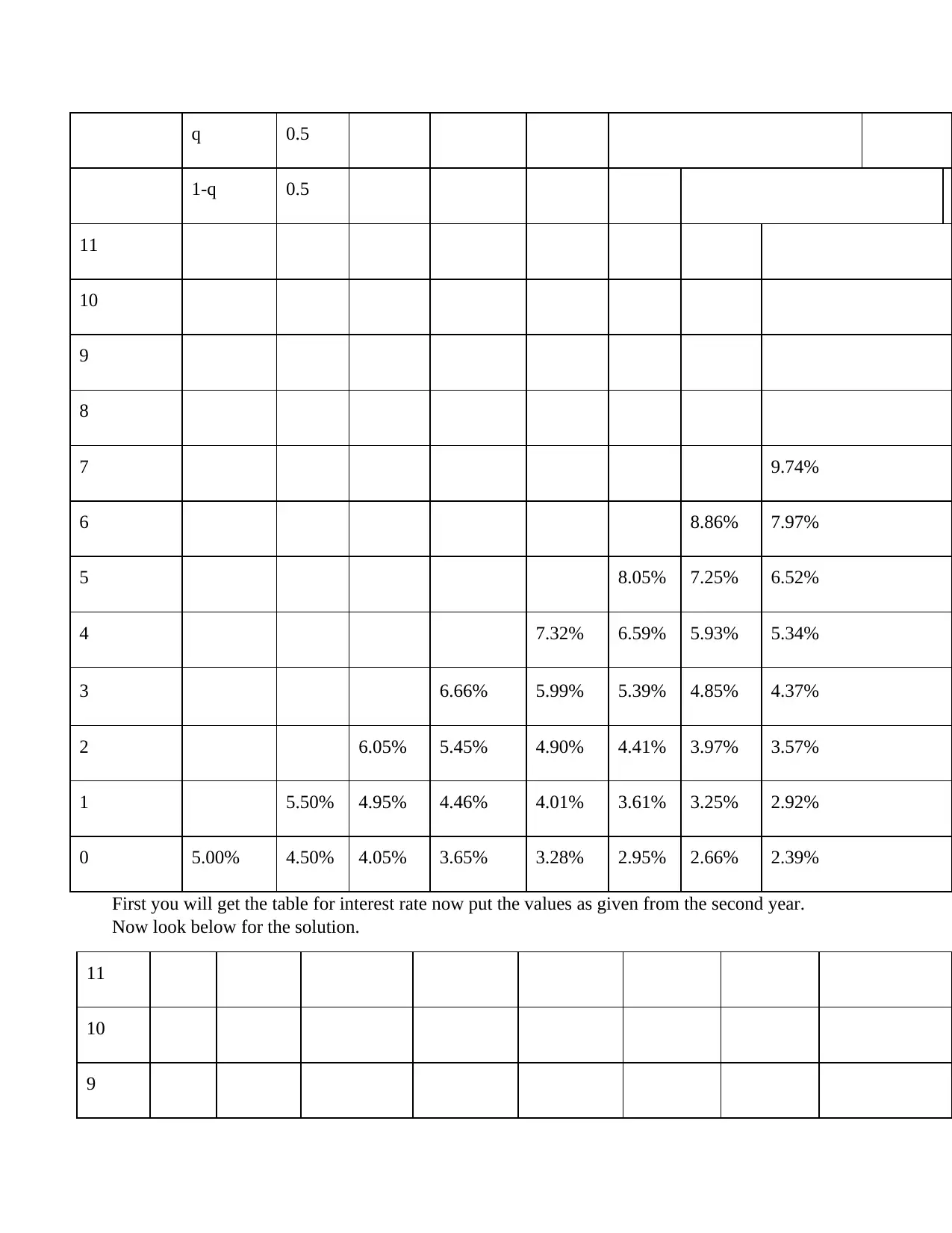
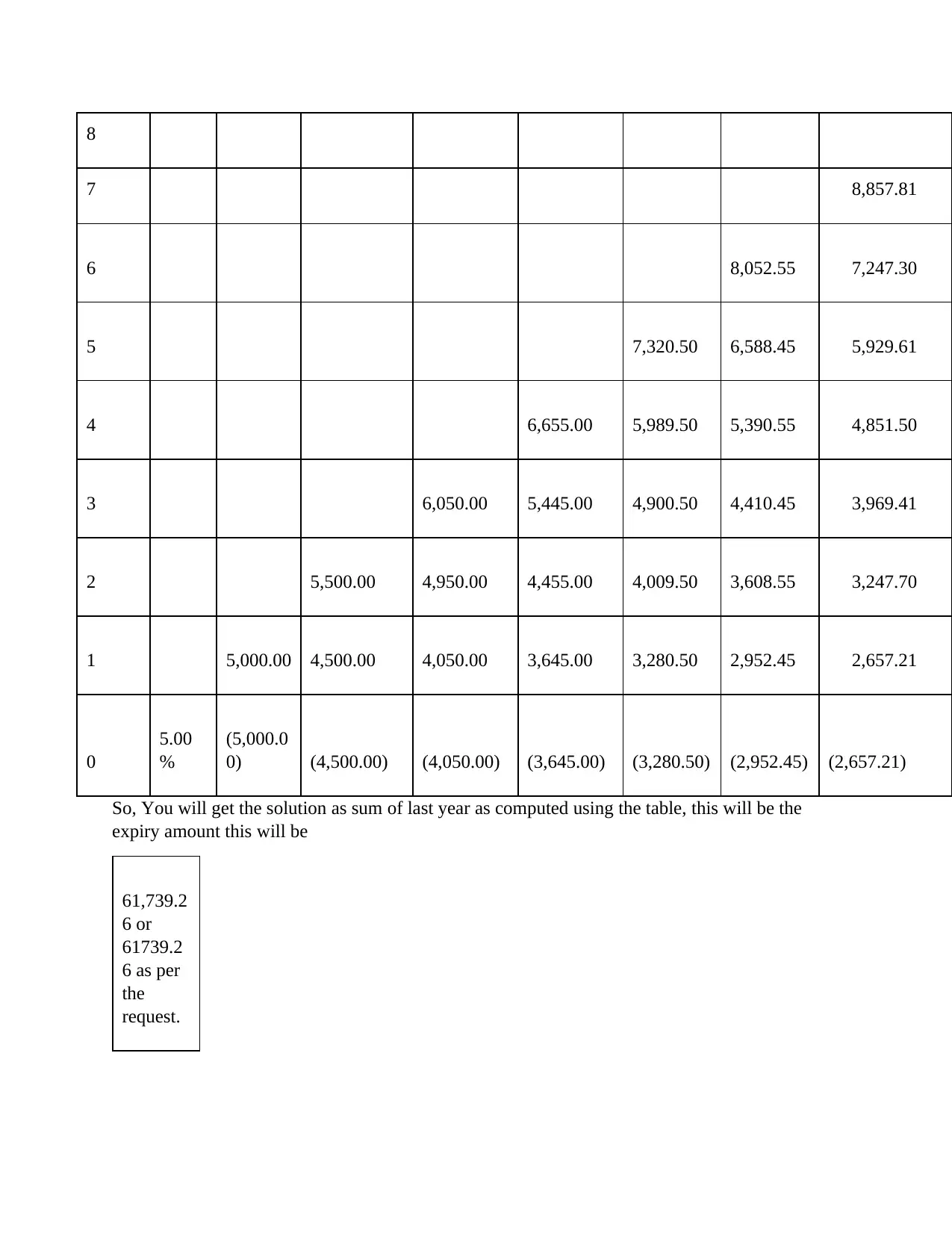
Pricing Zero-Coupon Bonds and Forward Contracts

This document explains the process of pricing zero-coupon bonds and forward contracts using interest rates and time to maturity. It provides step-by-step calculations and formulas for determining the prices of these financial instruments. The document also includes references for further reading on the topic.

1. Given
Face value of ZCB(F) = 100
Maturity time (t) = 10
Let we assume expected investor's required annual yield rate (r) = 10 %
price of a zero-coupon bond= P
P = F / [(1+r)^t]
hence
P=100/ [(1+.10)^10]
P= 38.55
2. Given
Spot price (P)= 38.55
Maturity time (t)= 4
(r)= 10%
So,
Forward price (A) = P*[(1+r)^t]
=38.55*[(1+.10)^4]
= 38.55*1.4641
= 56.44
3. Future price= spot price + carrying cost - returns
(a) spot price So=38.55
carring cost = So*[(1+r)^t] -- So
here r=10% and t=4
so carring cost = 17.89
returns =0 (in ZCB)

hence, initial Future price = 38.55+17.89
= 56.44
(b) spot price So=56.44
carring cost = So*[(1+r)^t] -- So
here r=10% and t=4
so carring cost = 26.19
returns =0 (in ZCB)
hence, initial Future price = 56.44+26.19
= 82.63
4. u = 1.1
d = .9
p of u = e^(r*t) - d / (u - d) = e^(.05*.5) - .9 / (1.1 - .9) = .6265
p of d = 1 - p of u = 1 - .6265 = .3734
Option value = Value of option on upside * p * e^(-r*t)
= 8*.6265 * e^(-.05*.5)
= 4.89
5. 676 answers
Fixed Rate 4.50%
Swap
expiration
Time
t=11
u 1.1
d 0.9

q 0.5
1-q 0.5
11
10
9
8
7 9.74%
6 8.86% 7.97%
5 8.05% 7.25% 6.52%
4 7.32% 6.59% 5.93% 5.34%
3 6.66% 5.99% 5.39% 4.85% 4.37%
2 6.05% 5.45% 4.90% 4.41% 3.97% 3.57%
1 5.50% 4.95% 4.46% 4.01% 3.61% 3.25% 2.92%
0 5.00% 4.50% 4.05% 3.65% 3.28% 2.95% 2.66% 2.39%
First you will get the table for interest rate now put the values as given from the second year.
Now look below for the solution.
11
10
9

8
7 8,857.81
6 8,052.55 7,247.30
5 7,320.50 6,588.45 5,929.61
4 6,655.00 5,989.50 5,390.55 4,851.50
3 6,050.00 5,445.00 4,900.50 4,410.45 3,969.41
2 5,500.00 4,950.00 4,455.00 4,009.50 3,608.55 3,247.70
1 5,000.00 4,500.00 4,050.00 3,645.00 3,280.50 2,952.45 2,657.21
0
5.00
%
(5,000.0
0) (4,500.00) (4,050.00) (3,645.00) (3,280.50) (2,952.45) (2,657.21)
So, You will get the solution as sum of last year as computed using the table, this will be the
expiry amount this will be
61,739.2
6 or
61739.2
6 as per
the
request.

6. Start at time i=10i=10.
For each node (10,j)(10,j) with j = 0,1,…,100,1,…,10, the forward price of the swap (ex
payments received at time 10) is a discounted, expected value:
S10,j=(1+r10,j)−1(12S11,j+12S11,j+1),S10,j=(1+r10,j)−1(12S11,j+12S11,j+1),
Where, for a receive fixed / pay float swap,
S10,j=1,000,000(0.045−f10,11,j)=1,000,000(0.045−r10,j).S10,j=1,000,000(0.045−f10,11,j)=1,00
0,000(0.045−r10,j).
Note that the forward rate f10,11,jf10,11,j equals r10,jr10,j on a tree where the time spacing
between the nodes matches the period for floating-rate resets and fixed rate payments.
Now find the forward swap price at each node (9,j)(9,j) with j = 0,1,…,90,1,…,9:
S9,j=(1+r9,j)−1(12S10,j+12S10,j+1+Q10,j),S9,j=(1+r9,j)−1(12S10,j+12S10,j+1+Q10,j),
Where the net payment received at time i=10i=10 is
Q10,j=1,000,000(0.045−f9,10,j)=1,000,000(0.045−r9,j).Q10,j=1,000,000(0.045−f9,10,j)=1,000,
000(0.045−r9,j).
Work your way back on the tree until you find the current swap price S0,0S0,0. Since this is a
forward starting swap beginning at time i=1i=1, do not include any net payments Q1,jQ1,j.
To price the swaption, set the terminal values at expiry i=5i=5 and j=0,1,…,5j=0,1,…,5 to
C5,j=max(S5,j,0).C5,j=max(S5,j,0).
Then work backwards from i=5i=5, calculating discounted expected values at each node until
you arrive at the current price C0,0C0,0.

References
Dai, Q., & Singleton, K. J. (2013). Specification analysis of affine term structure models. The
Journal of Finance, 55(5), 1943-1978.
Hull, J., & White, A. (2014). Numerical procedures for implementing term structure models I:
Single-factor models. Journal of derivatives, 2(1), 7-16.