Descriptive Statistics and Probability Assignment Solution - QBM117

This document presents a comprehensive solution to a QBM117 Business Statistics assignment. The solution covers descriptive statistics, including calculating clearance rates, creating pivot tables and bar charts, and analyzing house price data using descriptive statistics such as mean, media...Read More

1
QBM117 Business Statistics
Name:
Institution:

2
Question one
a. Table
Result Code Overall Outcome
PI, NB, VB property passed no bid vendor bid
SP, PN property sold prior not disclosed
S, SN property sold not disclosed
SA, SS sold after auction price not disclosed
W withdrawn prior to auction
KEY: S - property sold; SP - property sold prior; PI - property passed in; PN - sold prior
not disclosed; SN - sold not disclosed; NB - no bid; VB - vendor bid; W - withdrawn
prior to auction; SA - sold after auction; SS - sold after auction price not disclosed. N/A -
price or highest bid not available
b. Errors
i. Surry Hills, 71/175-189 Campbell St
ii. Queenscliff, 83 Queenscliff Rd
c. Pivot Table
d. Clearance rate of all properties
i. How many properties = 330
ii. S = 174 SP = 71 SA =1
iii. S = 174/330 = 52.72% SP = 21.52% SA =1/330 = 0.303 %
e. Clearance rate of four bedroom
i. Four-bedroom houses = 80
ii. S= 40 SP = 17 SA = 0
iii. S = 40/80 = 50% SP = 17/80 = 21.25%
iv. The clearance rate of four-bedroom houses is slightly lower compared to all
properties

3
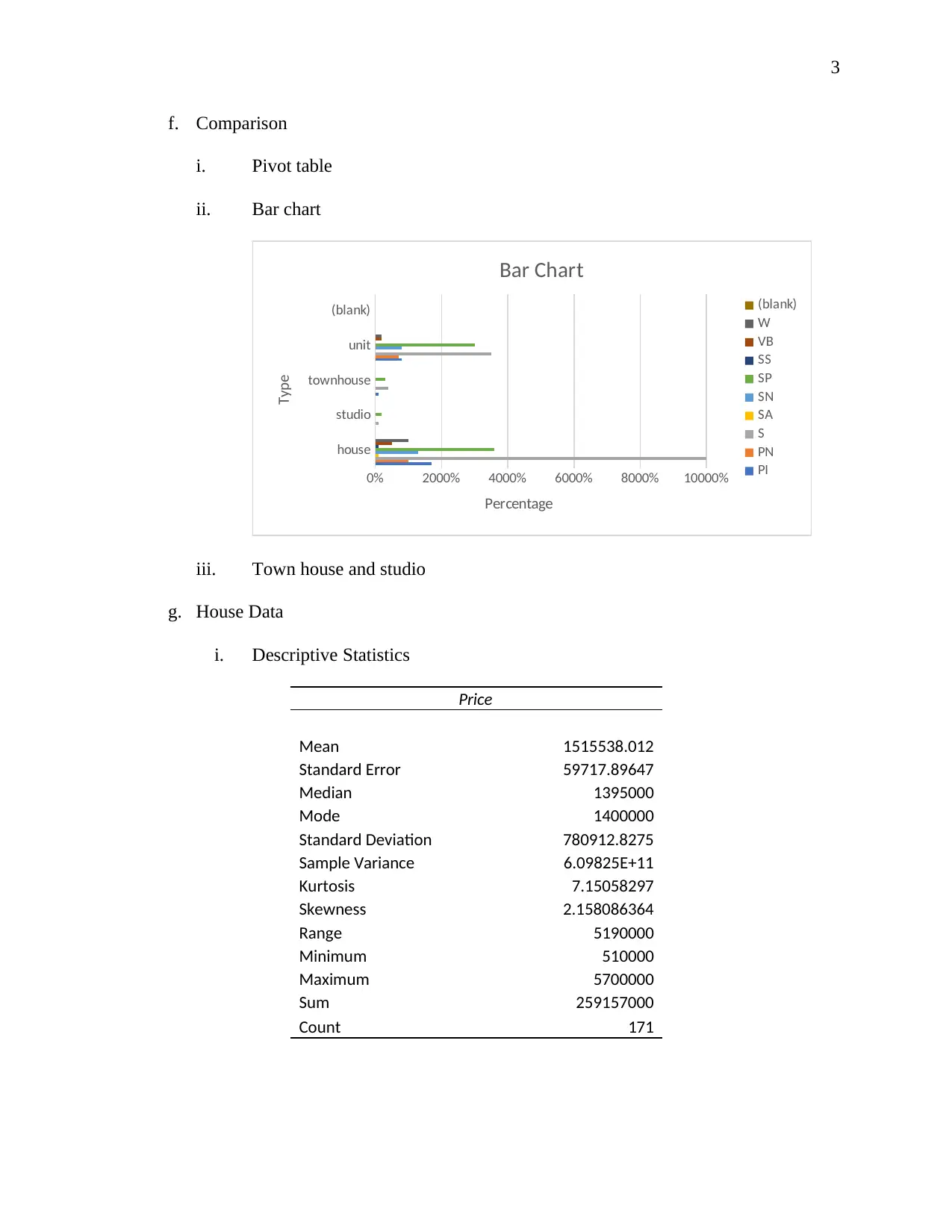
f. Comparison
i. Pivot table
ii. Bar chart
house
studio
townhouse
unit
(blank)
0% 2000% 4000% 6000% 8000% 10000%
Bar Chart
(blank)
W
VB
SS
SP
SN
SA
S
PN
PI
Percentage
Type
iii. Town house and studio
g. House Data
i. Descriptive Statistics
Price
Mean 1515538.012
Standard Error 59717.89647
Median 1395000
Mode 1400000
Standard Deviation 780912.8275
Sample Variance 6.09825E+11
Kurtosis 7.15058297
Skewness 2.158086364
Range 5190000
Minimum 510000
Maximum 5700000
Sum 259157000
Count 171

4
ii. Mean, median, and SD
Mean 1515538.012
Median 1395000
Standard Deviation 780900
iii. The cheapest house is worth $510,000. Moreover, it is a four-bedroom found
in Bateau Bay.
iv. Sample variance
Sample Variance
Actual number value 609,825,000,000
Scientific notation 6.09825*1011
h. Frequency distribution and Histogram
Frequecy distribution
Price Frequency
0-70 13
70-140 82
140-210 47
210-280 21
280-350 4
350-420 1
420-490 2
490-560 0
560-630 1
0-70 70-140 140-210 210-280 280-350 350-420 420-490 490-560 560-630
0
10
20
30
40
50
60
70
80
90
Histogram
Prices in $10,000
Frequency

5
i. As evident, unlike the mean, median price 1,395,000 is found in the most frequent
class size (700,000 to 1,400,000) thus it is recommendable to use the median in
quoting the selling price.
Question Two
Let M= Mastercard
V = Visa
A =American Express
P(M) = 0.3 P(MnA) = 0.04
P(V) = 0.6 P(MnV) = 0.07
P(A) = 0.1 P(VnA) = 0.03
a. P(VuM) = P(V) + P(M) – P(VnM)
= 0.6 + 0.3 – 0.07
= 0.83
b. P(V/M) = P(VnM)/P(M)
= 0.07/0.3
= 0.2333
c. For independence, P(V/M) = P(V)
As evident P(V/M) = 0.233 and P(V) = 0.6
0.233 ≠ 0.6
Therefore, the possession of a Mastercard is dependent on possession of Visacard.
d. For mutually exclusive events, P(AnV) = 0
However, P(AnV) = 0.03 thus they are not mutually exclusive.

6
Question Three
a. Let;
Company A = A
Company B = B
Order delivered Late = L
Order delivered on Time = L’
b. Tree diagram
c. P(L) = P(L’A) + P(L’B)
= 0.34 + 0.54 = 0.88
d. As evident, P(LB) = P(LA) = 0.06 thus both companies have an equal chance of
delivering the order late.
e. The probability 0.88 is above average thus the owner should not exhibit any concerns
rather express satisfaction.
A
B
0.4
0.6
L’
L
0.54
0.06
L
L’
0.06
0.34

7
Question 4
a. X assumes a binomial distribution because
i. Each market investor has the same probability (0.2) of being a retiree
ii. There is a fixed number of trials (25)
b. Parameters
P = 0.2
n = 25
c. P(5<= X <= 10)
Using statistical Tables
P(X<5) = P(4, 25, 0.2) = 0.4207
P(X<10) = P(10, 25, 0.2) = 0.9944
P(5<= X <= 10) = 0.9944 – 0.4207= 0.5737
d. P(X>= 10)
= P(9, 25, 0.2, TRUE) = 0.9827
1 - 0.9827 = 0.0173
e. Through the use of BINOM.DIST function
P(X<5) = BINOM.DIST(4, 25, 0.2, TRUE) = 0.420674309
P(X<10) = BINOM.DIST(10, 25, 0.2, TRUE) = 0.99444507
P(5<= X <= 10) = 0.99444507 – 0.420674309 = 0.57377
P(X>= 10)
= BINOM.DIST(9, 25, 0.2, TRUE) = 0.9826681
1 - 0.9826681 = 0.0173

8
f. 0.173 0R 1.73% show the chances that the total number of retirees is equal or greater
than 10.
g. E(X) = np = 25*0.2 = 5
Question 5
a. As evident, the breaking down of machine is unexpected (rare occasions); however,
there is a fixed quantity of moderate value (3) thus the distribution of X is given by
poisson distribution. Mean (λ) = 3
b. P= e− λ λx
x !
P(X<3) = P(2) + P(1) + P(0)
P= e−3 32
2! + e−3 31
1! + e−3 30
0!
= 0.2240 + 0.1494 + 0.0498
= 0.4232
c. P (X=7) P= e−3 37
7 ! = 0.0216
2*0.216 = 0.4320
d. Using the POISSON.DIST function
P(X<3) = POISSON.DIST(2,3,TRUE) = 0.4232
P(X=7) = =POISSON.DIST(7,3,FALSE) = 0.0216 * 2 = 0.4320

9
Question 6
a. The variable X assumes a normal distribution. Mean = 176.8 and Standard deviation
= 9.5. Therefore, X assumes N(176.8, 9.5)
b. P(X>200)
Z = (x-μ)/σ
= (200-176.8)/9.5 = 2.4421
P(2.4421)= 0.9927
1 – 0.9927 = 0.0073
c. P(147<=X<=168)
Z = (x-μ)/σ
= (147-176.8)/9.5 = -3.1368
P(-3.1368) = 0.00085
Z = (x-μ)/σ
= (168 - 176.8)/9.5 = -0.92632
= 0.1771
= 0.1771 – 0.00085 = 0.1763
d. P(X>=X1) = 0.02
1 - 0.02 = 0.98
Z(0.98) = 2.05
2.05 = (X – 176.8)/9.5
19.475 + 176.8 = X
196.275

10
e. Using the NORM.DIST function
P(X>200) =NORM.DIST(200,176.8,9.5, TRUE) = 0.992699
P(147<=X<=168)
P(X<=147) = NORM.DIST(147,176.8,9.5, TRUE) = 0.000845
P(X<=168) = NORM.DIST(168,176.8,9.5, TRUE) = 0.17714
Using NORM.INV function
Z(0.98) = NORM.INV(0.98,176.8,9.5) = 196.3106
f. Since the sample is drawn from the population then it assumes a normal distribution
with a mean of 176.8cm
g. Z= x −μ
σ
√ n
Therefore, Z=170−176.8
9.5
√40
Z = -4.5271
P = 0