University Physics: Rotational Motion Numerical Solutions Assignment
VerifiedAdded on 2023/01/17
|8
|1114
|77
Homework Assignment
AI Summary
This document presents a detailed solution to a physics assignment focusing on rotational motion. It includes a series of numerical problems covering key concepts such as moment of inertia, rotational kinetic energy, and angular momentum. The solutions are presented step-by-step, including the a...

1Rotational Motion Numericals
Rotational Motion Numericals
Rotational Motion Numericals
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
2Rotational Motion Numericals
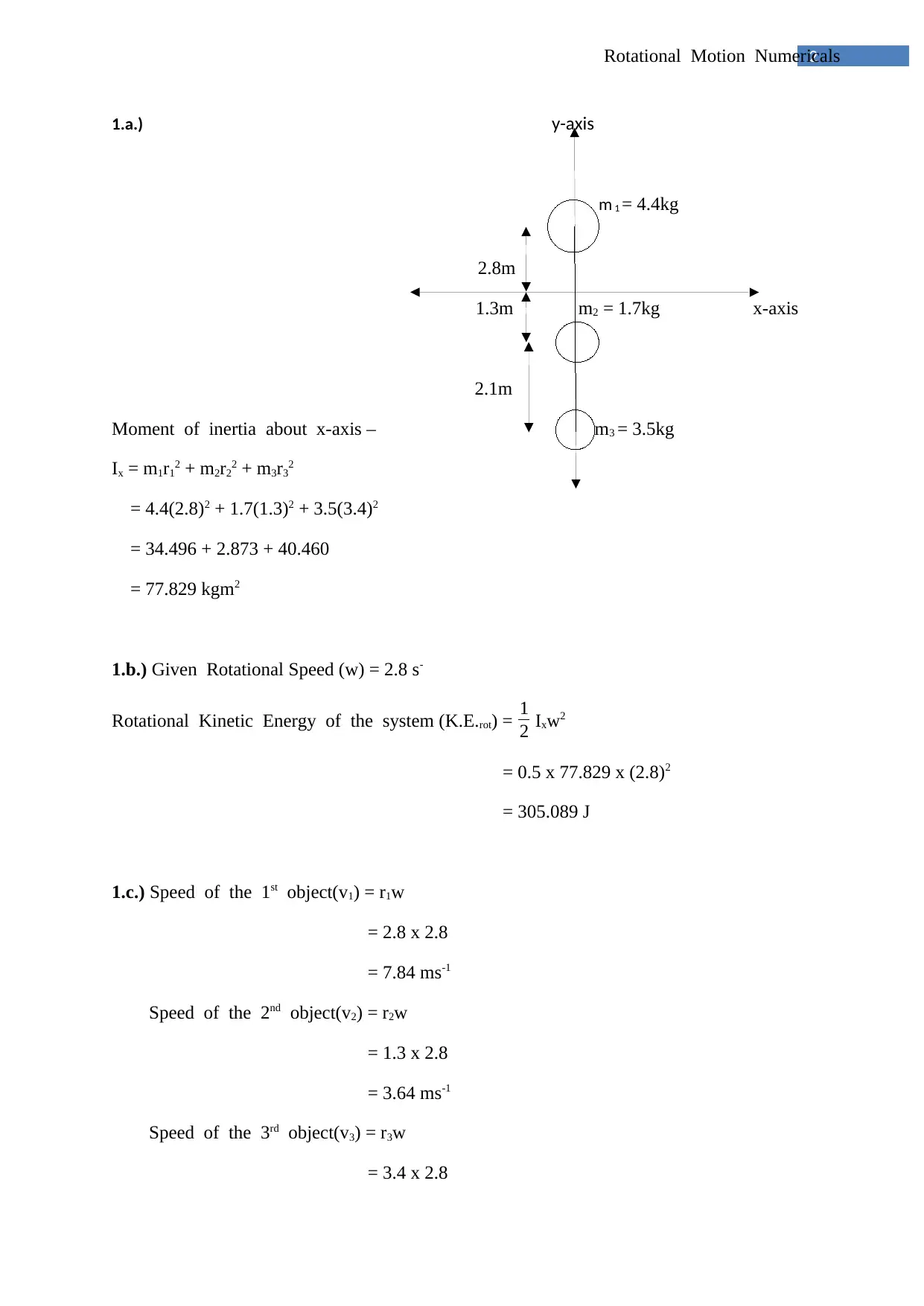
1.a.) y-axis
m 1 = 4.4kg
2.8m
1.3m m2 = 1.7kg x-axis
2.1m
Moment of inertia about x-axis – m3 = 3.5kg
Ix = m1r12 + m2r22 + m3r32
= 4.4(2.8)2 + 1.7(1.3)2 + 3.5(3.4)2
= 34.496 + 2.873 + 40.460
= 77.829 kgm2
1.b.) Given Rotational Speed (w) = 2.8 s-
Rotational Kinetic Energy of the system (K.E.rot) = 1
2 Ixw2
= 0.5 x 77.829 x (2.8)2
= 305.089 J
1.c.) Speed of the 1st object(v1) = r1w
= 2.8 x 2.8
= 7.84 ms-1
Speed of the 2nd object(v2) = r2w
= 1.3 x 2.8
= 3.64 ms-1
Speed of the 3rd object(v3) = r3w
= 3.4 x 2.8
1.a.) y-axis
m 1 = 4.4kg
2.8m
1.3m m2 = 1.7kg x-axis
2.1m
Moment of inertia about x-axis – m3 = 3.5kg
Ix = m1r12 + m2r22 + m3r32
= 4.4(2.8)2 + 1.7(1.3)2 + 3.5(3.4)2
= 34.496 + 2.873 + 40.460
= 77.829 kgm2
1.b.) Given Rotational Speed (w) = 2.8 s-
Rotational Kinetic Energy of the system (K.E.rot) = 1
2 Ixw2
= 0.5 x 77.829 x (2.8)2
= 305.089 J
1.c.) Speed of the 1st object(v1) = r1w
= 2.8 x 2.8
= 7.84 ms-1
Speed of the 2nd object(v2) = r2w
= 1.3 x 2.8
= 3.64 ms-1
Speed of the 3rd object(v3) = r3w
= 3.4 x 2.8

3Rotational Motion Numericals
= 9.52 ms-1
1.d.) Kinetic Energy of the 1st object(K.E.1) = 1
2m1v12
= 0.5 x 4.4 x (7.84)2
= 135.22 J
Kinetic Energy of the 2nd object(K.E.2) = 1
2m2v22
= 0.5 x 1.7 x (3.64)2
= 11.26 J
Kinetic Energy of the 3rd object(K.E.3) = 1
2m3v32
= 0.5 x 3.5 x (9.52)2
= 158.60 J
1.e.) Total Kinetic Energy (K.E.total) = 135.22 + 11.26 + 158.60
= 305.08 J
2.)
3.81m 0.19m
A B
m1 = 0.133kg O m2 = 64kg
Initially, the massless rod is horizontal. The mass m1 is projected horizontally when the
rod becomes vertical after rotating about the O. Since, only the gravitational force is
acting which is a conservative force, we can apply Law of Conservation of energy as
stated in Morin (2009) –
0 = m1g(OA) – m2g(OB) + 1
2m1(v)2 (v is the velocity with which m1 is projected)
0 = (0.133 x 9.8 x 3.81) – (64 x 9.8 x 0.19) + (0.5 x 0.133 x v2)
0.0665v2 = 119.1680 – 4.9659
= 9.52 ms-1
1.d.) Kinetic Energy of the 1st object(K.E.1) = 1
2m1v12
= 0.5 x 4.4 x (7.84)2
= 135.22 J
Kinetic Energy of the 2nd object(K.E.2) = 1
2m2v22
= 0.5 x 1.7 x (3.64)2
= 11.26 J
Kinetic Energy of the 3rd object(K.E.3) = 1
2m3v32
= 0.5 x 3.5 x (9.52)2
= 158.60 J
1.e.) Total Kinetic Energy (K.E.total) = 135.22 + 11.26 + 158.60
= 305.08 J
2.)
3.81m 0.19m
A B
m1 = 0.133kg O m2 = 64kg
Initially, the massless rod is horizontal. The mass m1 is projected horizontally when the
rod becomes vertical after rotating about the O. Since, only the gravitational force is
acting which is a conservative force, we can apply Law of Conservation of energy as
stated in Morin (2009) –
0 = m1g(OA) – m2g(OB) + 1
2m1(v)2 (v is the velocity with which m1 is projected)
0 = (0.133 x 9.8 x 3.81) – (64 x 9.8 x 0.19) + (0.5 x 0.133 x v2)
0.0665v2 = 119.1680 – 4.9659
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

4Rotational Motion Numericals
v2 = 114.2021/0.0665
v = 41.44 ms-1
3.) Dimensions of the tire are given in the question-
Volume of the tire (V) = 2Vside walls + Vtread
= 2(π(33.72 - 17.32) 0.76) + π(36.72 – 33.72)19.4
= 3991.97 + 12865.46
= 16857.43 cm3
Mass of each side wall (m1) = 1.25 x 1995.99
= 2494.98 g
Mass of the tread of tire (m2) = 1.25 x 12865.46
= 16081.25 g
Moment of Inertia of the tire when it turns (I)
= [m2(19.4)2/12 + m2(33.72 + 36.72)/4] + 2[m1(0.76)2/12 + m1(33.72 + 17.32)/4 +
m1(8.94)2]
= 16081.25(31.36 + 620.65) + 4989.96(0.048 + 358.75 + 79.92)
= 10485135.81 + 2189185.27
= 12675321.08 gcm2
= 1.27 kg m2
4.)
m1 = 3.65kg CM m2 = 5.26kg
r1 r2
1.14m
Accoding to Goldstein(2011), m1r1 = m2r2
3.65r1 = 5.26r2
v2 = 114.2021/0.0665
v = 41.44 ms-1
3.) Dimensions of the tire are given in the question-
Volume of the tire (V) = 2Vside walls + Vtread
= 2(π(33.72 - 17.32) 0.76) + π(36.72 – 33.72)19.4
= 3991.97 + 12865.46
= 16857.43 cm3
Mass of each side wall (m1) = 1.25 x 1995.99
= 2494.98 g
Mass of the tread of tire (m2) = 1.25 x 12865.46
= 16081.25 g
Moment of Inertia of the tire when it turns (I)
= [m2(19.4)2/12 + m2(33.72 + 36.72)/4] + 2[m1(0.76)2/12 + m1(33.72 + 17.32)/4 +
m1(8.94)2]
= 16081.25(31.36 + 620.65) + 4989.96(0.048 + 358.75 + 79.92)
= 10485135.81 + 2189185.27
= 12675321.08 gcm2
= 1.27 kg m2
4.)
m1 = 3.65kg CM m2 = 5.26kg
r1 r2
1.14m
Accoding to Goldstein(2011), m1r1 = m2r2
3.65r1 = 5.26r2
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
5Rotational Motion Numericals
Also, r1 + r2 = 1.14
1.44r2 + r2 = 1.14
r2 = 0.47m
So, r1 = 0.67m
Now, Moment of Inertia of the system around the center of mass (I)-
I = m1r12 + m2r22
= 3.65(0.67)2 + 5.26(0.47)2
= 1.64 + 1.16
= 2.8 kg m2
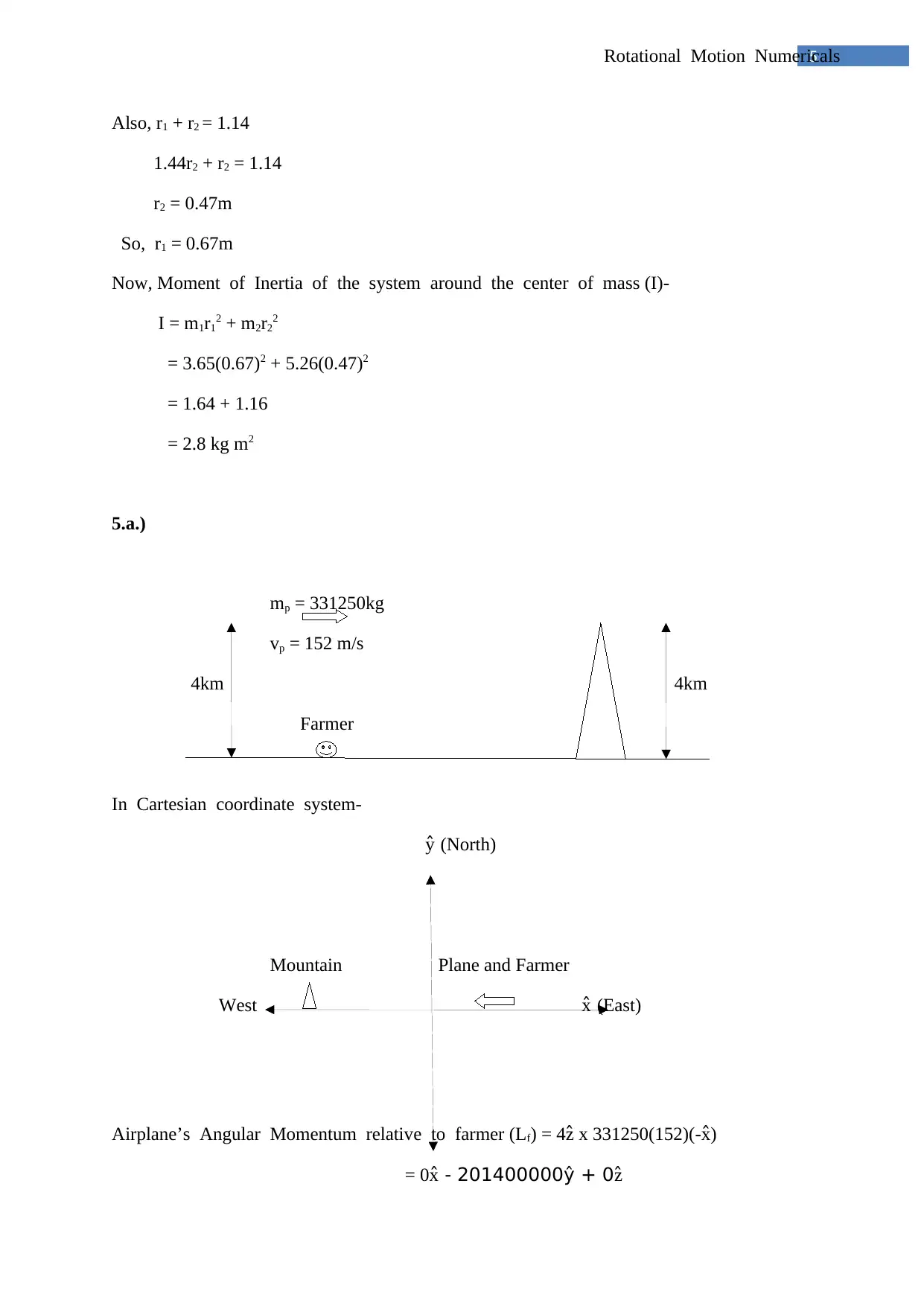
5.a.)
mp = 331250kg
vp = 152 m/s
4km 4km
Farmer
In Cartesian coordinate system-
ŷ (North)
Mountain Plane and Farmer
West x̂ (East)
Airplane’s Angular Momentum relative to farmer (Lf) = 4ẑ x 331250(152)(-x̂ )
= 0x̂ - 201400000ŷ + 0 ẑ
Also, r1 + r2 = 1.14
1.44r2 + r2 = 1.14
r2 = 0.47m
So, r1 = 0.67m
Now, Moment of Inertia of the system around the center of mass (I)-
I = m1r12 + m2r22
= 3.65(0.67)2 + 5.26(0.47)2
= 1.64 + 1.16
= 2.8 kg m2
5.a.)
mp = 331250kg
vp = 152 m/s
4km 4km
Farmer
In Cartesian coordinate system-
ŷ (North)
Mountain Plane and Farmer
West x̂ (East)
Airplane’s Angular Momentum relative to farmer (Lf) = 4ẑ x 331250(152)(-x̂ )
= 0x̂ - 201400000ŷ + 0 ẑ

6Rotational Motion Numericals
5.b.) Airplane’s Angular Momentum relative to Mountain peak(Lm)
= 282000x̂ X 331250(152)(-x̂ )
= 0x̂ + 0ŷ + 0 ẑ
Since, x̂ X x̂ = 0
6.a.)
v
m M
Dimensions of the board are given in the question
Velocity of the bullet reduces by ¼ after passing through the board.
Since, there is no non-conservative force acting here, we can apply law of
conservation of energy at the moment when the bullet strikes the board-
1
2mv2 = 1
2Iw2 + 1
2mv’2
Here, I is the moment of inertia of the board of length(a) and width (b)
w is the angular velocity of the board
v’ is the reduced velocity of the board
0.5 x 0.146 x v2 = 0.5 x w2 x Ma2/3 + 0.5 x 0.146 x (3v/4)2
0.073v2 = 3.87w2 + 0.041v2
v2 =3.87w2/0.032
v2 = 120.93w2
In order to rotate the board in complete circle, its minimum velocity must be √ 6 gr
Here. r is the distance between center of mass of board and the axle.
5.b.) Airplane’s Angular Momentum relative to Mountain peak(Lm)
= 282000x̂ X 331250(152)(-x̂ )
= 0x̂ + 0ŷ + 0 ẑ
Since, x̂ X x̂ = 0
6.a.)
v
m M
Dimensions of the board are given in the question
Velocity of the bullet reduces by ¼ after passing through the board.
Since, there is no non-conservative force acting here, we can apply law of
conservation of energy at the moment when the bullet strikes the board-
1
2mv2 = 1
2Iw2 + 1
2mv’2
Here, I is the moment of inertia of the board of length(a) and width (b)
w is the angular velocity of the board
v’ is the reduced velocity of the board
0.5 x 0.146 x v2 = 0.5 x w2 x Ma2/3 + 0.5 x 0.146 x (3v/4)2
0.073v2 = 3.87w2 + 0.041v2
v2 =3.87w2/0.032
v2 = 120.93w2
In order to rotate the board in complete circle, its minimum velocity must be √ 6 gr
Here. r is the distance between center of mass of board and the axle.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

7Rotational Motion Numericals
So,
v2 = 120.93 x ( √6 gr
r )2
v2 = 120.93 x [(6 x 9.8)/0.955]
v2 = 7445.74
v = 86.29 m/s
6.b.)In case the bullet is embedded in the board, the conservation of energy statement
will be changed to-
1
2mv2 = 1
2Iw2 + 1
2I’w2
Here, I’ is the moment of inertia of the bullet around the axle.
So,
0.5 x 0.146 x v2 = (0.5 x w2 x Ma2/3) + (0.5 x ma2 x w2)
0.073v2 = 3.87w2 + 0.267w2
0.073v2 = 4.137w2
In order to complete the circle, w must be equal to √ ( M +2 m
M +3 m )6 g /a
0.073v2 = 4.137 [ 6.652
6.798 x 6 x 9.8
1.91 ]
v2 = 1707.17
v = 41.32 m/s
References-
Goldstein, H.(2011). Classical Mechanics. Chennai : Pearson Publications
So,
v2 = 120.93 x ( √6 gr
r )2
v2 = 120.93 x [(6 x 9.8)/0.955]
v2 = 7445.74
v = 86.29 m/s
6.b.)In case the bullet is embedded in the board, the conservation of energy statement
will be changed to-
1
2mv2 = 1
2Iw2 + 1
2I’w2
Here, I’ is the moment of inertia of the bullet around the axle.
So,
0.5 x 0.146 x v2 = (0.5 x w2 x Ma2/3) + (0.5 x ma2 x w2)
0.073v2 = 3.87w2 + 0.267w2
0.073v2 = 4.137w2
In order to complete the circle, w must be equal to √ ( M +2 m
M +3 m )6 g /a
0.073v2 = 4.137 [ 6.652
6.798 x 6 x 9.8
1.91 ]
v2 = 1707.17
v = 41.32 m/s
References-
Goldstein, H.(2011). Classical Mechanics. Chennai : Pearson Publications
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

8Rotational Motion Numericals
Morin, D. (2009). Introduction to Classical Mechanics. New Delhi : Cambridge University
Press
Morin, D. (2009). Introduction to Classical Mechanics. New Delhi : Cambridge University
Press
1 out of 8
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.