Victoria University MATH 132 Assignment 6: Trigonometry and Triangles
VerifiedAdded on 2023/03/20
|14
|1850
|78
Homework Assignment
AI Summary
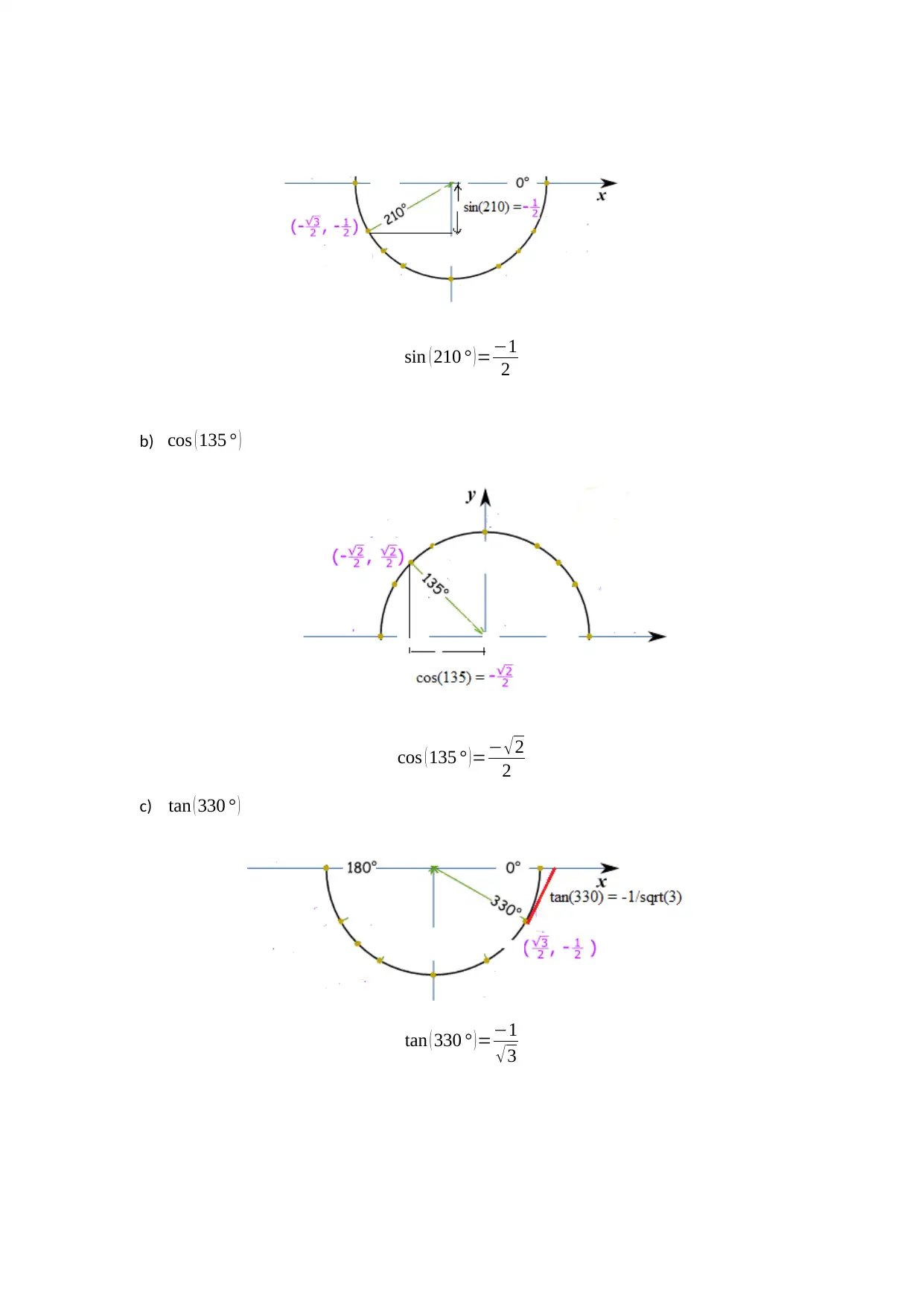
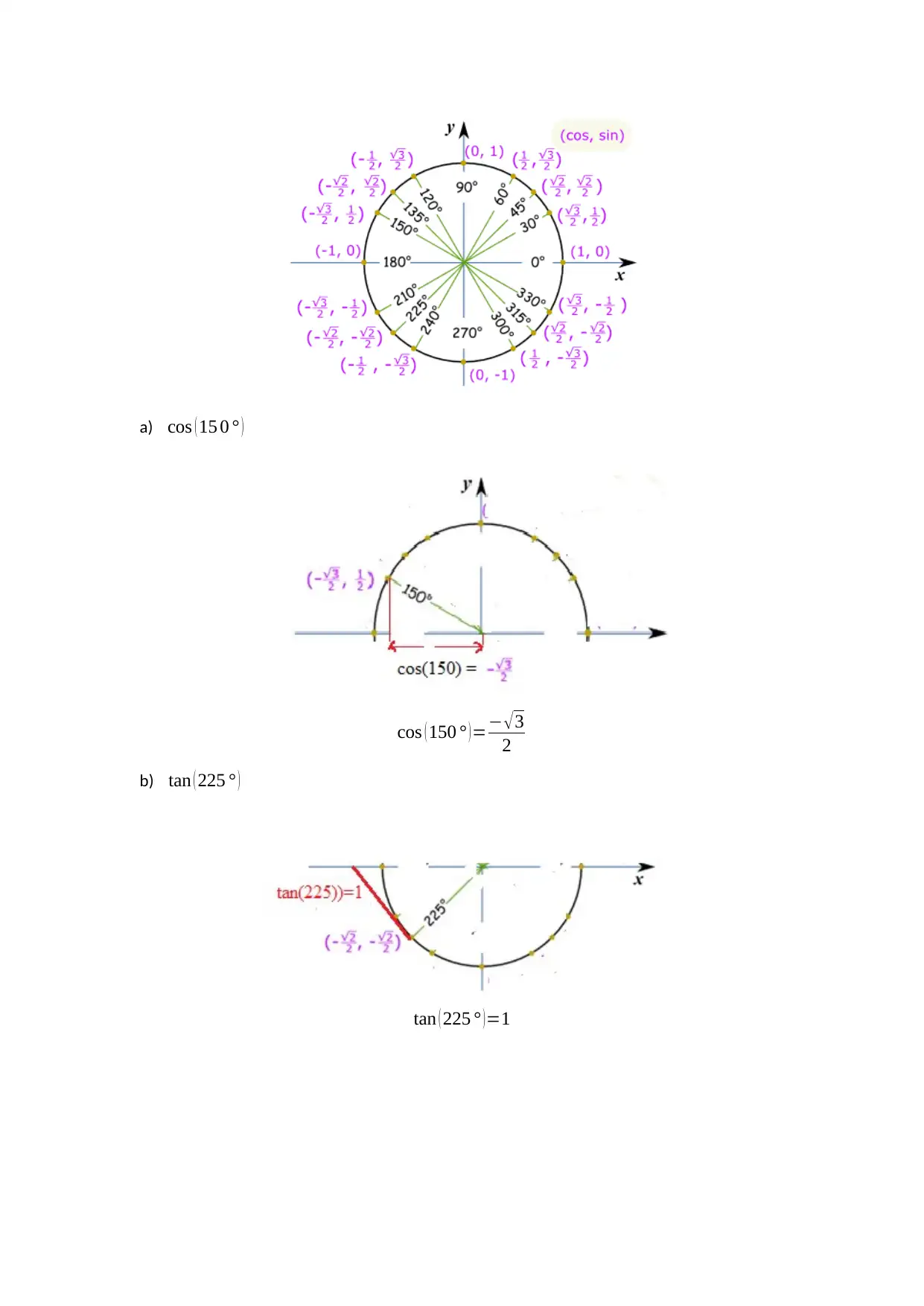
This document presents a comprehensive solution to Assignment 6 for MATH 132, focusing on fundamental trigonometric concepts and their applications. The solution begins by calculating trigonometric ratios (sine, cosine, and tangent) using Pythagorean triples and the Law of Sines, demonstrating the relationships between angles and sides in right-angled triangles. It then applies the Pythagorean theorem to determine unknown side lengths in various triangles. The assignment also explores geometric constructions, showing how a right-angled triangle can be divided into two isosceles triangles. Furthermore, the solution utilizes the unit circle to calculate trigonometric ratios for different angles, including sine, cosine, and tangent values. It continues by calculating the area of a triangle using the formula involving sine and finds the length of a dotted line, applying Pythagoras' theorem. The solution concludes by testing triangle inequalities to determine if given side lengths can form triangles and calculating the area of triangles using Heron's formula. The document contains figures and diagrams to illustrate each concept. Finally, the solution provides tutorial exercises with similar questions and solutions.
1 out of 14
















![[object Object]](/_next/static/media/star-bottom.7253800d.svg)