Operations Management: Inventory Management Principles and Models
VerifiedAdded on 2022/01/22
|76
|5467
|442
Presentation
AI Summary
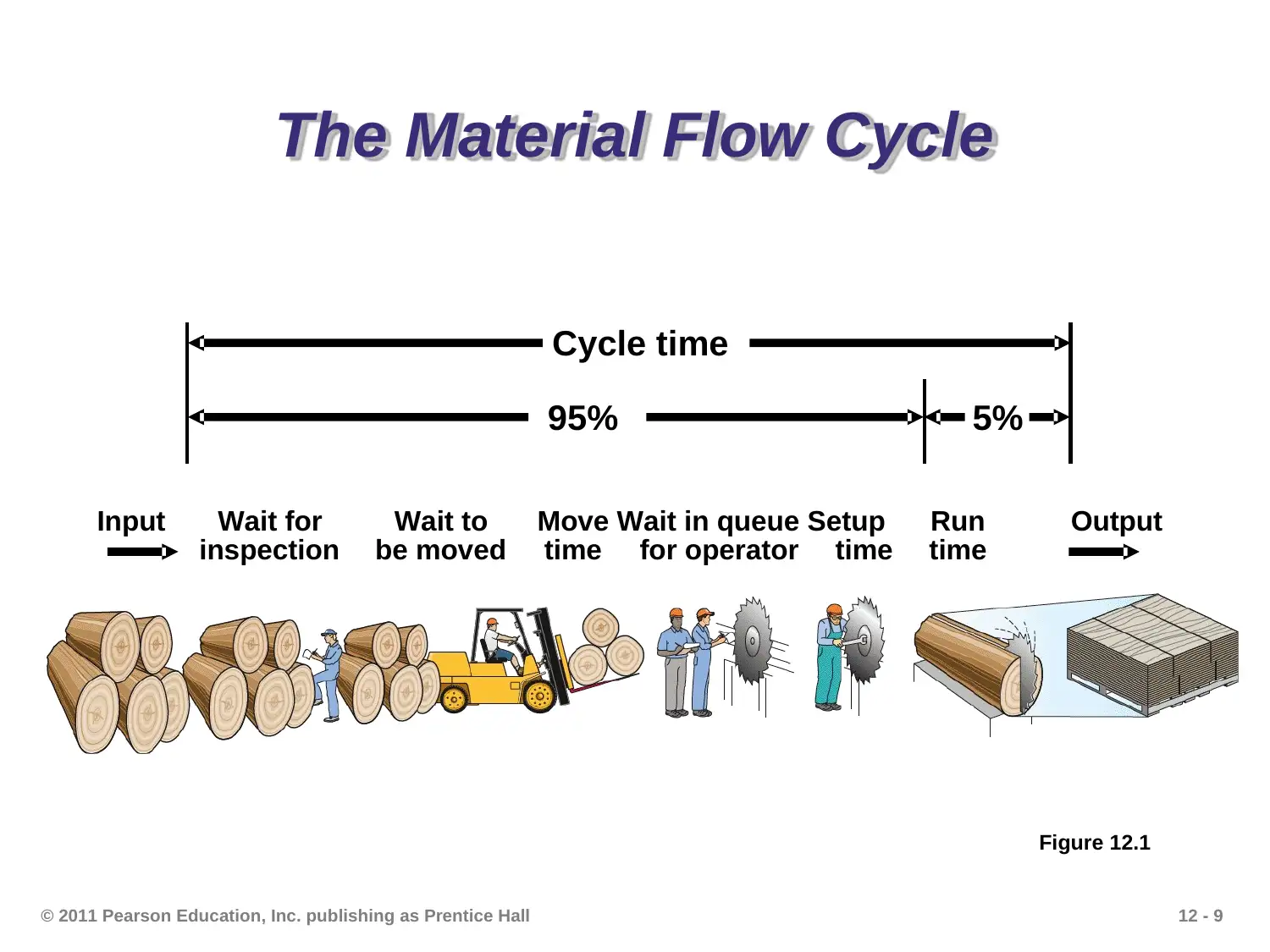
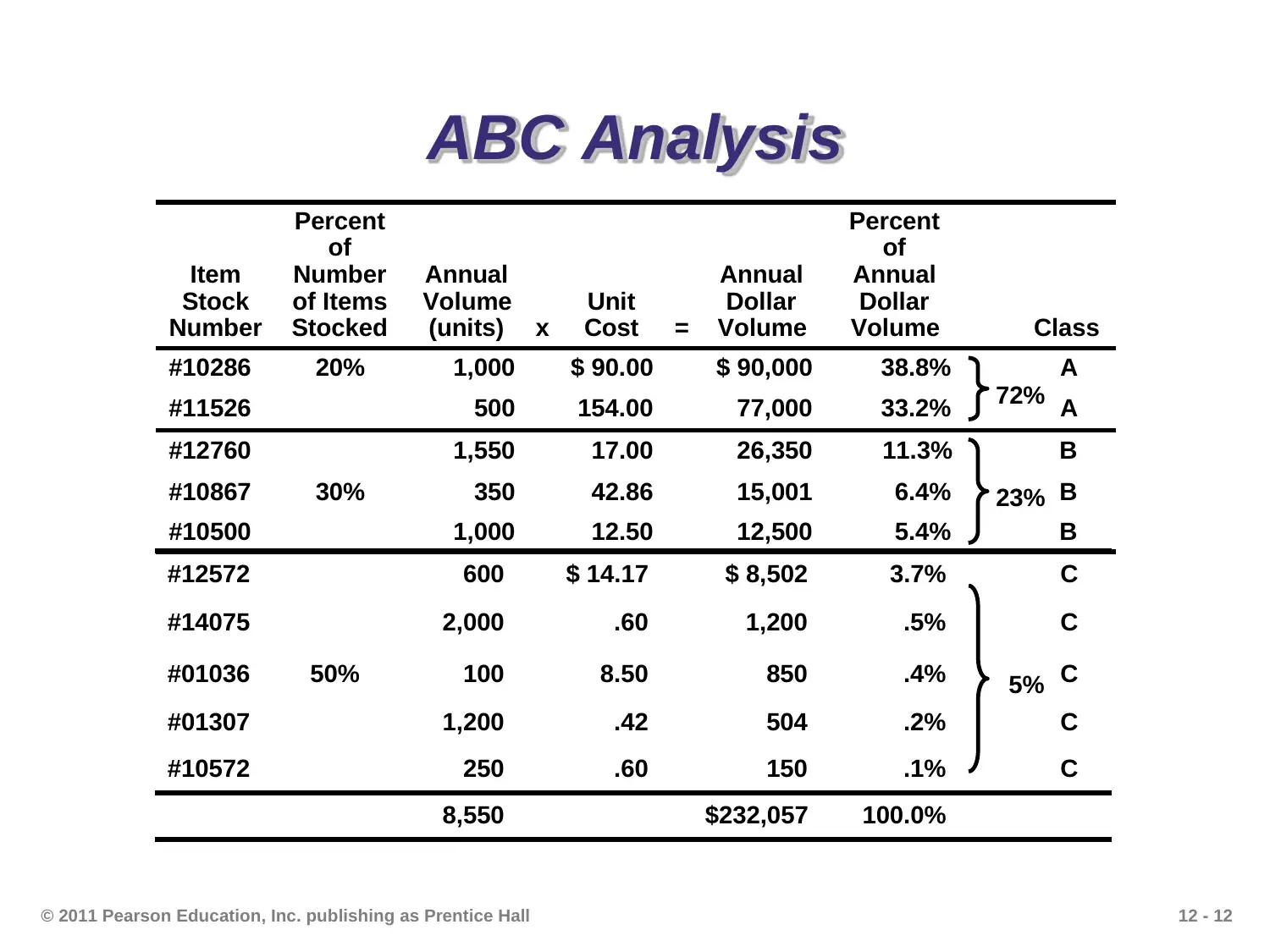
This PowerPoint presentation provides a comprehensive overview of inventory management, a critical aspect of operations management. It begins by highlighting the importance of inventory, its functions, and the various types, including raw materials, work-in-process, MRO, and finished goods. The presentation then delves into key inventory management techniques, such as ABC analysis, which categorizes inventory items based on their annual dollar volume, and cycle counting, a method for maintaining accurate inventory records. It also covers the control of service inventories. The presentation further explores inventory models for independent demand, including the basic Economic Order Quantity (EOQ) model, the production order quantity model, and quantity discount models. It explains the concepts of holding costs, ordering costs, and setup costs, and demonstrates how to minimize total costs. Reorder points, safety stock, and probabilistic models are also discussed, providing a complete understanding of inventory management principles and practices. This is a valuable resource for students studying operations management.
1 out of 76











![[object Object]](/_next/static/media/star-bottom.7253800d.svg)