Questions and Answers of Data Science

1
Data Science
Student’s Name
Affiliation
Course
Instructor
Date

2
Question 1
A random variable V has a density fv(v) =Kv2 exp(-b/v2 )
a) What is the distribution of a new random variable, Y=1/2 mV2
The first step will entail differentiation of the function fv(v) =Kv2 exp(-b/v2 ) w.r.t V
d (f ( v ))
d(v ) =2KV* exp (-b/v2) + KV2*-2e-bv-3
The distribution for the new variable is given by
F(y)= 2KV* exp (-b/v2) + KV2*-2e-bv-3
b) in order to get the mean of y one has to differentiate y with respect to V and get the
d (f ( y ) )
d( y) = MV
The mean of Y=MV
Question 2
Que. A
> # the expected value of a binomial distribution is given by np
> #n is the number of observations
> #p is the number of success
> #p=6/10
> #n=10
> #let expected value be represented by M
> p<-6/10
> n<-10
> M<-p*n
> M

3
[1] 6
> #this means that the mean is 6
Rcode:
Que B
The posterior distribution is given by
P(Ɵ) ={ p=3/5 for x=1,2.....10
The estimated value for (Ɵ) is =Ɵ/6 where 6 is the mean of the distribution
Que. C
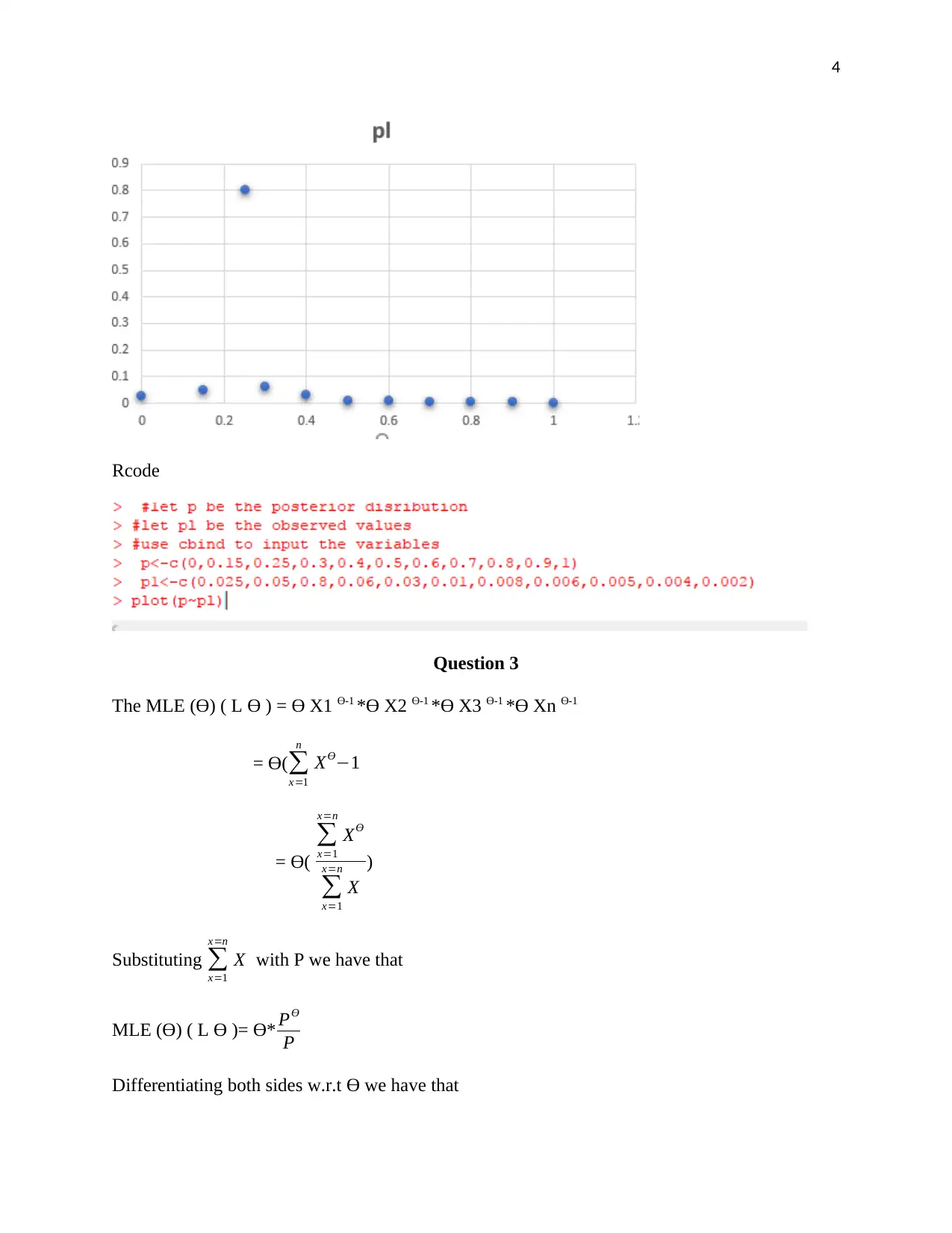
> p<-c(0,0.15,0.25,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1)
> p1<-c(0.025,0.05,0.8,0.06,0.03,0.01,0.008,0.006,0.005,0.004,0.002)
> plot(p~pl)