CIV3204: Analysis of Streamflow and Rainfall Data - Assignment 2019
VerifiedAdded on 2022/10/01
|9
|1369
|177
Project
AI Summary
This project analyzes streamflow and rainfall data for the Woori Yallock catchment, focusing on sampling distributions and hypothesis testing. The analysis begins by randomly selecting data and calculating sampling distributions using histograms and descriptive statistics like skewness and kurtosis. The project then calculates probabilities for daily average streamflow exceeding specific values using t-tests. Further, the assignment utilizes ANOVA and the Tukey-Kramer procedure to test for differences in mean streamflow across different time periods. Finally, the project examines variability changes over time using F-tests, connecting findings to broader environmental concerns like global warming and water resource management. The student's solution covers methods, calculations, interpretations, and conclusions for each part of the assignment, demonstrating a comprehensive understanding of statistical analysis applied to hydrological data.
2.3-Sampling Distribution and Hypothesis Testing
PART 1
Question 1: Method to calculate the sampling distributions
The first step was randomly selecting 100 values and subjecting them to 100, 200, and 1000
iterations. In order to do this successful an excel function was used to select random data values
for the 1999 dataset (i.e.
=INDEX($A$2:$A$1737,RANDBETWEEN(1,COUNTA($A$2:$A$1737)),1). This function
was used to populate a table of value with sample size (100) on the left side and iterations
(100,200, or 1000) on the top. The values where then copied and pasted back into the same
position (void of the function) to prevent the continuous refreshing of values usually caused by
the “RandBetween” function.
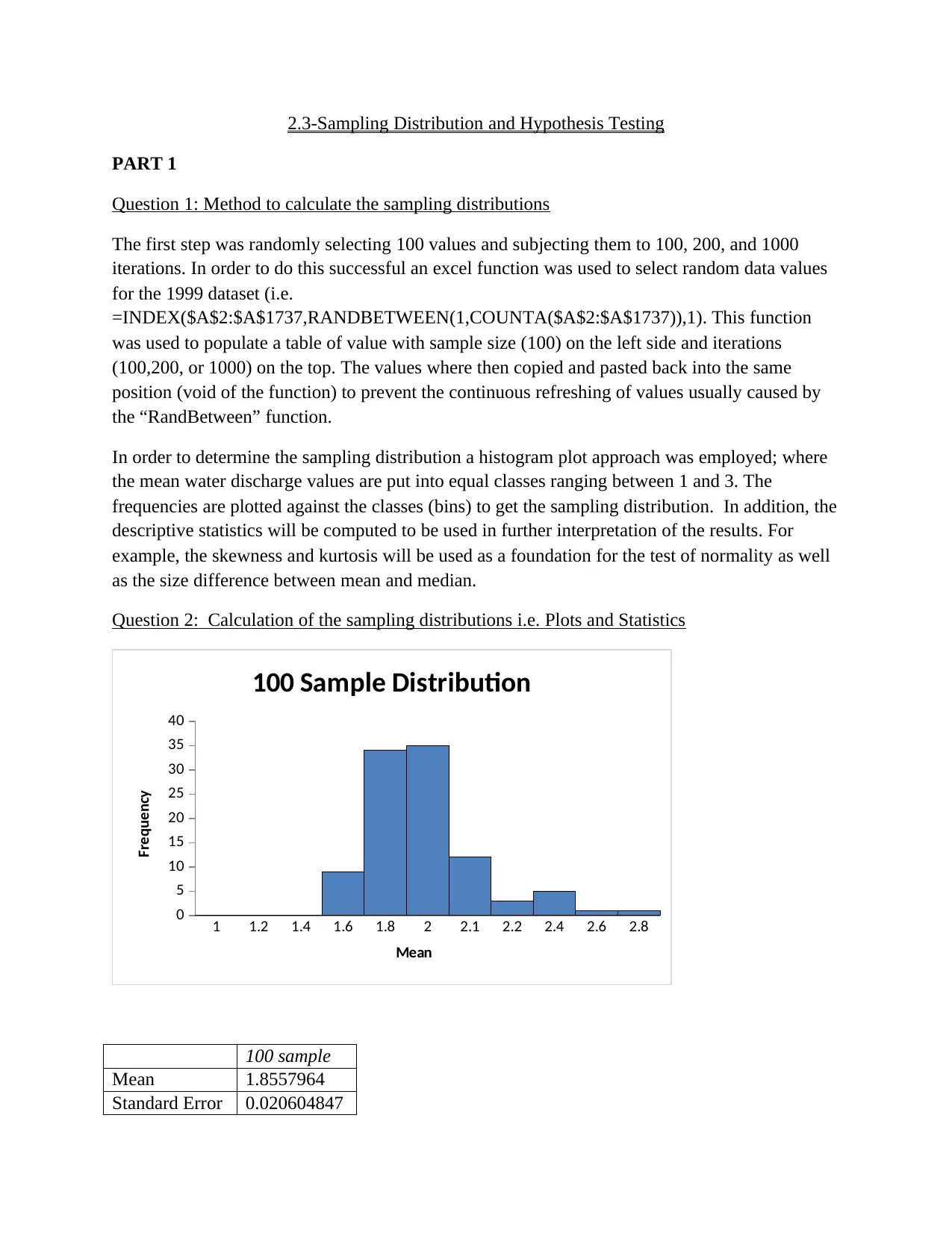
In order to determine the sampling distribution a histogram plot approach was employed; where
the mean water discharge values are put into equal classes ranging between 1 and 3. The
frequencies are plotted against the classes (bins) to get the sampling distribution. In addition, the
descriptive statistics will be computed to be used in further interpretation of the results. For
example, the skewness and kurtosis will be used as a foundation for the test of normality as well
as the size difference between mean and median.
Question 2: Calculation of the sampling distributions i.e. Plots and Statistics
1 1.2 1.4 1.6 1.8 2 2.1 2.2 2.4 2.6 2.8
0
5
10
15
20
25
30
35
40
100 Sample Distribution
Mean
Frequency
100 sample
Mean 1.8557964
Standard Error 0.020604847
PART 1
Question 1: Method to calculate the sampling distributions
The first step was randomly selecting 100 values and subjecting them to 100, 200, and 1000
iterations. In order to do this successful an excel function was used to select random data values
for the 1999 dataset (i.e.
=INDEX($A$2:$A$1737,RANDBETWEEN(1,COUNTA($A$2:$A$1737)),1). This function
was used to populate a table of value with sample size (100) on the left side and iterations
(100,200, or 1000) on the top. The values where then copied and pasted back into the same
position (void of the function) to prevent the continuous refreshing of values usually caused by
the “RandBetween” function.
In order to determine the sampling distribution a histogram plot approach was employed; where
the mean water discharge values are put into equal classes ranging between 1 and 3. The
frequencies are plotted against the classes (bins) to get the sampling distribution. In addition, the
descriptive statistics will be computed to be used in further interpretation of the results. For
example, the skewness and kurtosis will be used as a foundation for the test of normality as well
as the size difference between mean and median.
Question 2: Calculation of the sampling distributions i.e. Plots and Statistics
1 1.2 1.4 1.6 1.8 2 2.1 2.2 2.4 2.6 2.8
0
5
10
15
20
25
30
35
40
100 Sample Distribution
Mean
Frequency
100 sample
Mean 1.8557964
Standard Error 0.020604847
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Median 1.835425
Mode #N/A
Standard
Deviation
0.206048468
Sample
Variance
0.042455971
Kurtosis 1.36986228
Skewness 0.843467534
Range 1.18166
Minimum 1.47124
Maximum 2.6529
Sum 185.57964
Count 100
1 1.2 1.4 1.6 1.8 2 2.1 2.2 2.4 2.6 2.8 3
0
10
20
30
40
50
60
70
80
200 Sample Distribution
Mean
Frequency
200 Sample
Mean 1.806265
Standard Error 0.014062
Median 1.804865
Mode #N/A
Standard
Deviation
0.198874
Sample
Variance
0.039551
Kurtosis 2.316882
Skewness 0.869112
Mode #N/A
Standard
Deviation
0.206048468
Sample
Variance
0.042455971
Kurtosis 1.36986228
Skewness 0.843467534
Range 1.18166
Minimum 1.47124
Maximum 2.6529
Sum 185.57964
Count 100
1 1.2 1.4 1.6 1.8 2 2.1 2.2 2.4 2.6 2.8 3
0
10
20
30
40
50
60
70
80
200 Sample Distribution
Mean
Frequency
200 Sample
Mean 1.806265
Standard Error 0.014062
Median 1.804865
Mode #N/A
Standard
Deviation
0.198874
Sample
Variance
0.039551
Kurtosis 2.316882
Skewness 0.869112
Range 1.36011
Minimum 1.35779
Maximum 2.7179
Sum 361.253
Count 200
1 1.2 1.4 1.6 1.8 2 2.1 2.2 2.4 2.6 2.8 3
0
50
100
150
200
250
300
350
400
1000 Sample Distribution
Mean
Frequency
1000 Sample
Mean 1.842174
Standard Error 0.00645
Median 1.825495
Mode #N/A
Standard
Deviation
0.203981
Sample
Variance
0.041608
Kurtosis 0.272112
Skewness 0.452909
Range 1.37319
Minimum 1.35053
Maximum 2.72372
Sum 1842.174
Count 1000
Question 3: Conclusion (Interpreting the results)
Minimum 1.35779
Maximum 2.7179
Sum 361.253
Count 200
1 1.2 1.4 1.6 1.8 2 2.1 2.2 2.4 2.6 2.8 3
0
50
100
150
200
250
300
350
400
1000 Sample Distribution
Mean
Frequency
1000 Sample
Mean 1.842174
Standard Error 0.00645
Median 1.825495
Mode #N/A
Standard
Deviation
0.203981
Sample
Variance
0.041608
Kurtosis 0.272112
Skewness 0.452909
Range 1.37319
Minimum 1.35053
Maximum 2.72372
Sum 1842.174
Count 1000
Question 3: Conclusion (Interpreting the results)
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

The 100-values sample does seem to follow a normal distribution in spite of the fact it is a little
bit skewed to the right. Looking at the skewness and kurtosis values we can see that they are
both within the acceptable range for normality to be assumed i.e. Skewness is between -2 and 2
while Kurtosis is between -4 and 4. Hence, we can conclude that the sampling distribution is
normal
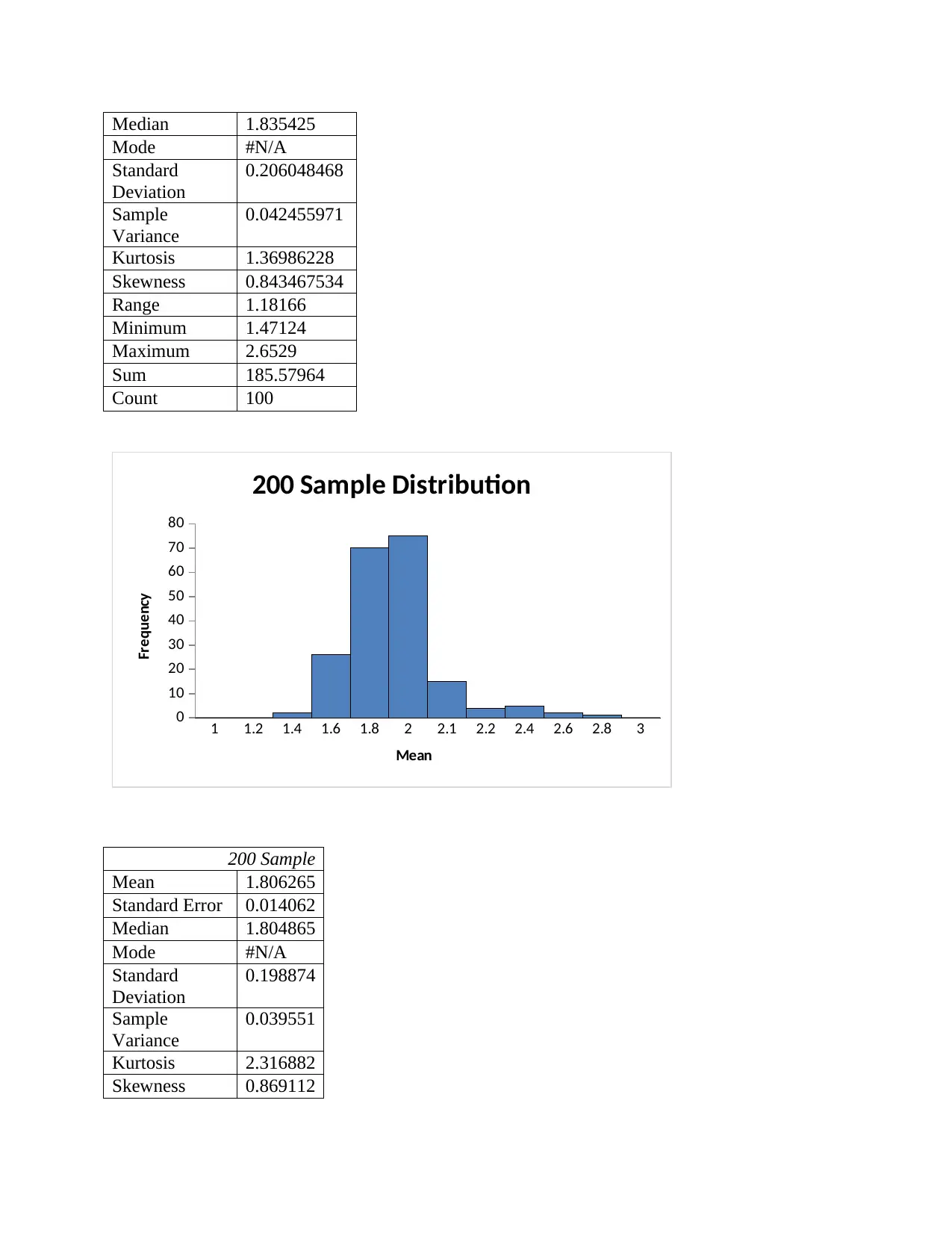
Similarly, the histogram for the 200-values sample indicates that the discharge follows a
Gaussian/Normal distribution. This is further confirmed by the skewness and kurtosis values of
0.8 and 2.3 respectively. There two values prove that the sample data is normally distributed.
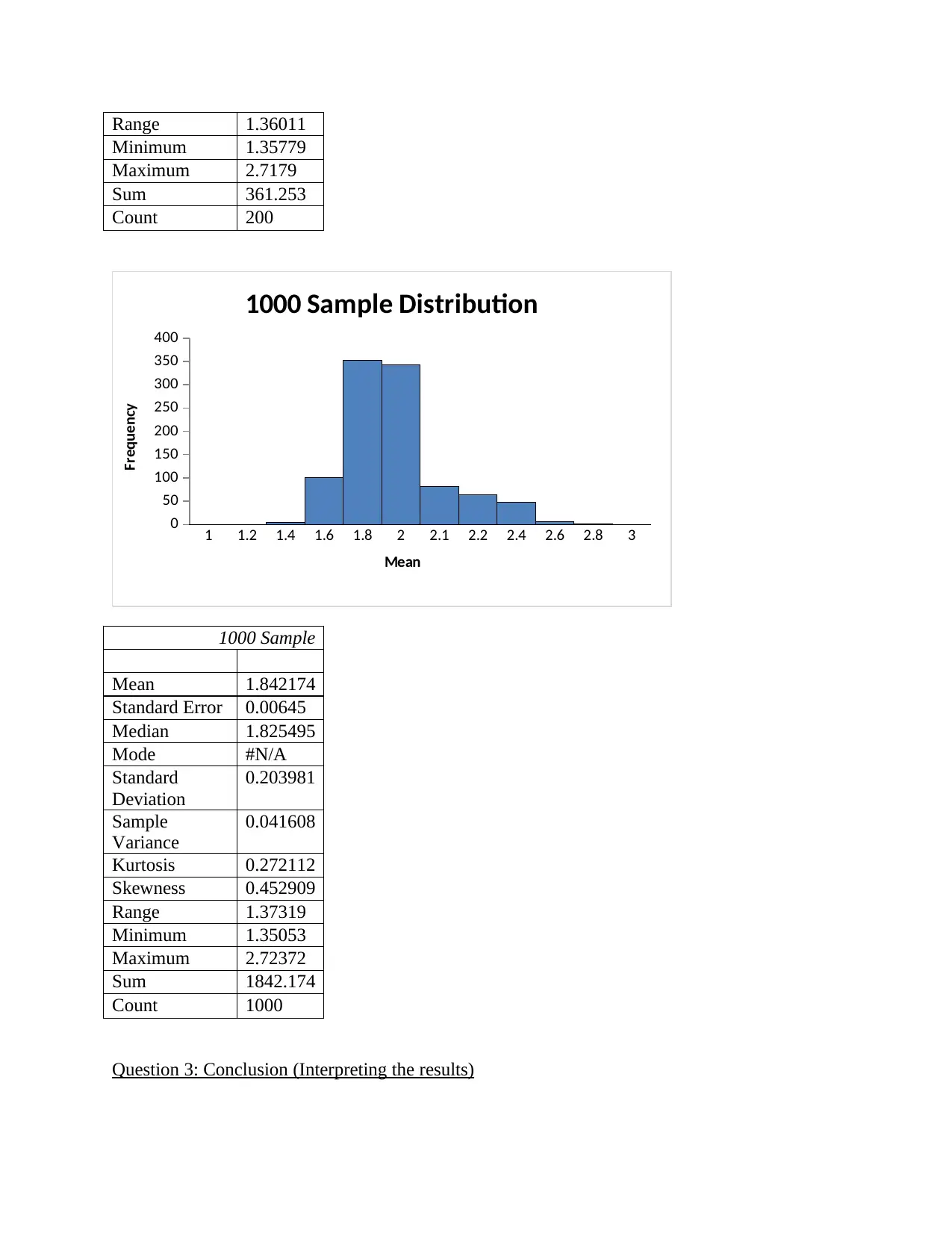
The third and last chart also indicates that the 1000-value sample also follows a Gaussian
distribution; a fact that is solidified by the skewness and kurtosis scores of 0.6 and 0.4
respectively. Hence, all three histogram are in a way similar meaning that the data for water
discharge does indeed follow a Gaussian distribution. Similarly, all three samples have means
and medians that are almost similar indicating normality in the sampling distribution.
PART B
Question 1: Method to calculate the probability of the daily average being larger than the
specified values
We will take a random sample of 24 observation from the 1999 water discharge dataset (using
the excel function previously discussed) and use that data to compute its mean and standard
deviation. We are going to assume that the data sample is random, and follows a normal
distribution; as such, we will use the formula below to calculate probability given than the
sample size (n) is less than 30.
t= X−μ
s/ √n
Where X is the sample mean and μ is the population mean and σ is the population Standard
deviation
The resulting t value plus degrees of freedom (24-1=23) will be used to look up the probability
that P(X<x) for x=0.5, 1, 2 and 3 from the Student T-tables. In order to get the desired values of
P(X>x) we will perform the following function:
P ( X > x ) =1−P ( X < x )
The mean and standard deviation for the 24 observations are 1.475083 and 1.474495 respectively
Question 2: Calculation of each of the four values (and Interpretation)
Probability Daily Average (x) is
Greater Than 0.5
bit skewed to the right. Looking at the skewness and kurtosis values we can see that they are
both within the acceptable range for normality to be assumed i.e. Skewness is between -2 and 2
while Kurtosis is between -4 and 4. Hence, we can conclude that the sampling distribution is
normal
Similarly, the histogram for the 200-values sample indicates that the discharge follows a
Gaussian/Normal distribution. This is further confirmed by the skewness and kurtosis values of
0.8 and 2.3 respectively. There two values prove that the sample data is normally distributed.
The third and last chart also indicates that the 1000-value sample also follows a Gaussian
distribution; a fact that is solidified by the skewness and kurtosis scores of 0.6 and 0.4
respectively. Hence, all three histogram are in a way similar meaning that the data for water
discharge does indeed follow a Gaussian distribution. Similarly, all three samples have means
and medians that are almost similar indicating normality in the sampling distribution.
PART B
Question 1: Method to calculate the probability of the daily average being larger than the
specified values
We will take a random sample of 24 observation from the 1999 water discharge dataset (using
the excel function previously discussed) and use that data to compute its mean and standard
deviation. We are going to assume that the data sample is random, and follows a normal
distribution; as such, we will use the formula below to calculate probability given than the
sample size (n) is less than 30.
t= X−μ
s/ √n
Where X is the sample mean and μ is the population mean and σ is the population Standard
deviation
The resulting t value plus degrees of freedom (24-1=23) will be used to look up the probability
that P(X<x) for x=0.5, 1, 2 and 3 from the Student T-tables. In order to get the desired values of
P(X>x) we will perform the following function:
P ( X > x ) =1−P ( X < x )
The mean and standard deviation for the 24 observations are 1.475083 and 1.474495 respectively
Question 2: Calculation of each of the four values (and Interpretation)
Probability Daily Average (x) is
Greater Than 0.5
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

t score -3.2386
P(x<0.5) 0.0018
P(x>0.5) 0.9982
Greater Than 1
t score -1.57792
P(x<1) 0.0641
P(x>1) 0.9359
Greater Than 2
t score 1.743433
P(x<2) 0.9527
P(x>2) 0.0473
Greater Than 3
t score 5.064786
P(x<3) 1
P(x>3) 0
The probability that the average daily water discharge is greater that 0.5 is 99.82% while the
probability that it is greater than 3 is 0%. This means that the average daily water discharge is
between 0 and 3 m3s-1
PART C
Question 1: Method to set up the ANOVA
We will set up four columns each for the four treatments in excel. The number of observations in
each column is not important. We will then go into excel data tab, then data analysis and select
single factor ANOVA. We will select out data and set the alpha level. Our intension is to test the
hypothesis that there is no difference in the average daily steam-flow across the four treatments
(time periods).
Null Hypothesis: All the means are the same i.e. U1=U2=U3=U4
Alternative Hypothesis: At least one of the means is different
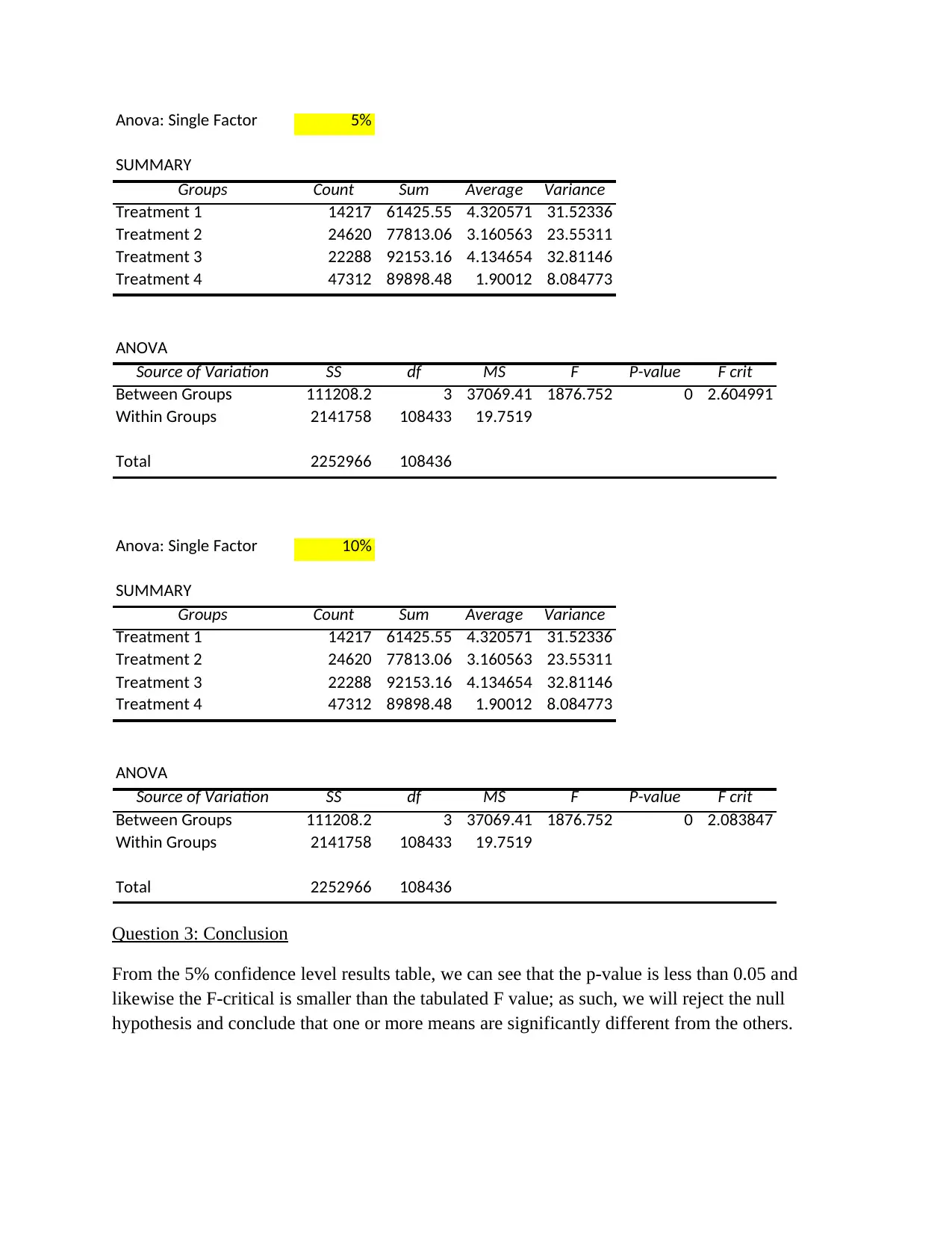
Question 2: Calculation of the entries in the ANOVA table:
The two tables are the one-way ANOVA results for 5% and 10% confidence level
P(x<0.5) 0.0018
P(x>0.5) 0.9982
Greater Than 1
t score -1.57792
P(x<1) 0.0641
P(x>1) 0.9359
Greater Than 2
t score 1.743433
P(x<2) 0.9527
P(x>2) 0.0473
Greater Than 3
t score 5.064786
P(x<3) 1
P(x>3) 0
The probability that the average daily water discharge is greater that 0.5 is 99.82% while the
probability that it is greater than 3 is 0%. This means that the average daily water discharge is
between 0 and 3 m3s-1
PART C
Question 1: Method to set up the ANOVA
We will set up four columns each for the four treatments in excel. The number of observations in
each column is not important. We will then go into excel data tab, then data analysis and select
single factor ANOVA. We will select out data and set the alpha level. Our intension is to test the
hypothesis that there is no difference in the average daily steam-flow across the four treatments
(time periods).
Null Hypothesis: All the means are the same i.e. U1=U2=U3=U4
Alternative Hypothesis: At least one of the means is different
Question 2: Calculation of the entries in the ANOVA table:
The two tables are the one-way ANOVA results for 5% and 10% confidence level
Anova: Single Factor 5%
SUMMARY
Groups Count Sum Average Variance
Treatment 1 14217 61425.55 4.320571 31.52336
Treatment 2 24620 77813.06 3.160563 23.55311
Treatment 3 22288 92153.16 4.134654 32.81146
Treatment 4 47312 89898.48 1.90012 8.084773
ANOVA
Source of Variation SS df MS F P-value F crit
Between Groups 111208.2 3 37069.41 1876.752 0 2.604991
Within Groups 2141758 108433 19.7519
Total 2252966 108436
Anova: Single Factor 10%
SUMMARY
Groups Count Sum Average Variance
Treatment 1 14217 61425.55 4.320571 31.52336
Treatment 2 24620 77813.06 3.160563 23.55311
Treatment 3 22288 92153.16 4.134654 32.81146
Treatment 4 47312 89898.48 1.90012 8.084773
ANOVA
Source of Variation SS df MS F P-value F crit
Between Groups 111208.2 3 37069.41 1876.752 0 2.083847
Within Groups 2141758 108433 19.7519
Total 2252966 108436
Question 3: Conclusion
From the 5% confidence level results table, we can see that the p-value is less than 0.05 and
likewise the F-critical is smaller than the tabulated F value; as such, we will reject the null
hypothesis and conclude that one or more means are significantly different from the others.
SUMMARY
Groups Count Sum Average Variance
Treatment 1 14217 61425.55 4.320571 31.52336
Treatment 2 24620 77813.06 3.160563 23.55311
Treatment 3 22288 92153.16 4.134654 32.81146
Treatment 4 47312 89898.48 1.90012 8.084773
ANOVA
Source of Variation SS df MS F P-value F crit
Between Groups 111208.2 3 37069.41 1876.752 0 2.604991
Within Groups 2141758 108433 19.7519
Total 2252966 108436
Anova: Single Factor 10%
SUMMARY
Groups Count Sum Average Variance
Treatment 1 14217 61425.55 4.320571 31.52336
Treatment 2 24620 77813.06 3.160563 23.55311
Treatment 3 22288 92153.16 4.134654 32.81146
Treatment 4 47312 89898.48 1.90012 8.084773
ANOVA
Source of Variation SS df MS F P-value F crit
Between Groups 111208.2 3 37069.41 1876.752 0 2.083847
Within Groups 2141758 108433 19.7519
Total 2252966 108436
Question 3: Conclusion
From the 5% confidence level results table, we can see that the p-value is less than 0.05 and
likewise the F-critical is smaller than the tabulated F value; as such, we will reject the null
hypothesis and conclude that one or more means are significantly different from the others.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
From the 10% confidence level results table, we can see that the p-value is less than 0.1 and
likewise the F-critical is smaller than the tabulated F value; as such, we will reject the null
hypothesis and conclude that one or more means are significantly different from the others.
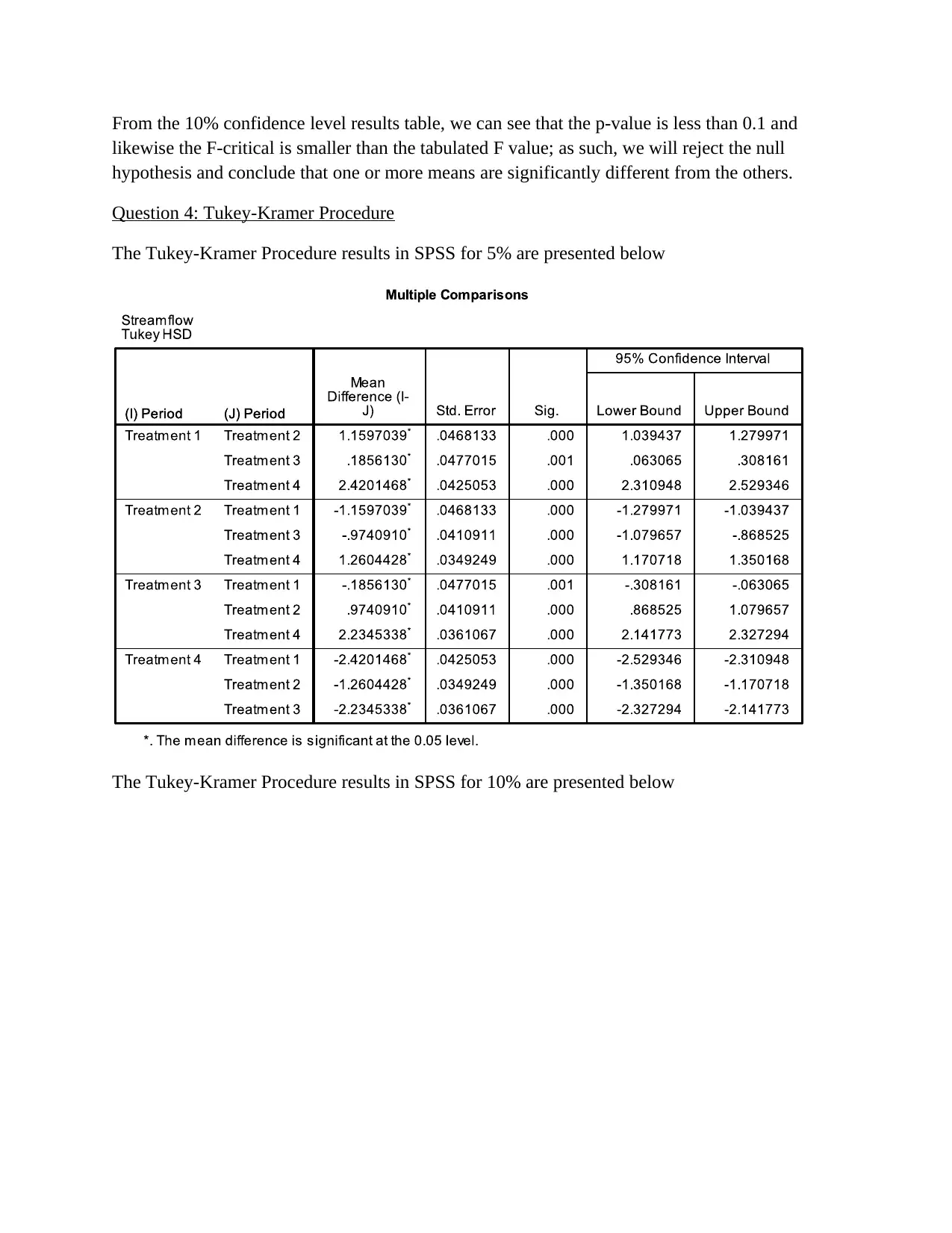
Question 4: Tukey-Kramer Procedure
The Tukey-Kramer Procedure results in SPSS for 5% are presented below
The Tukey-Kramer Procedure results in SPSS for 10% are presented below
likewise the F-critical is smaller than the tabulated F value; as such, we will reject the null
hypothesis and conclude that one or more means are significantly different from the others.
Question 4: Tukey-Kramer Procedure
The Tukey-Kramer Procedure results in SPSS for 5% are presented below
The Tukey-Kramer Procedure results in SPSS for 10% are presented below
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
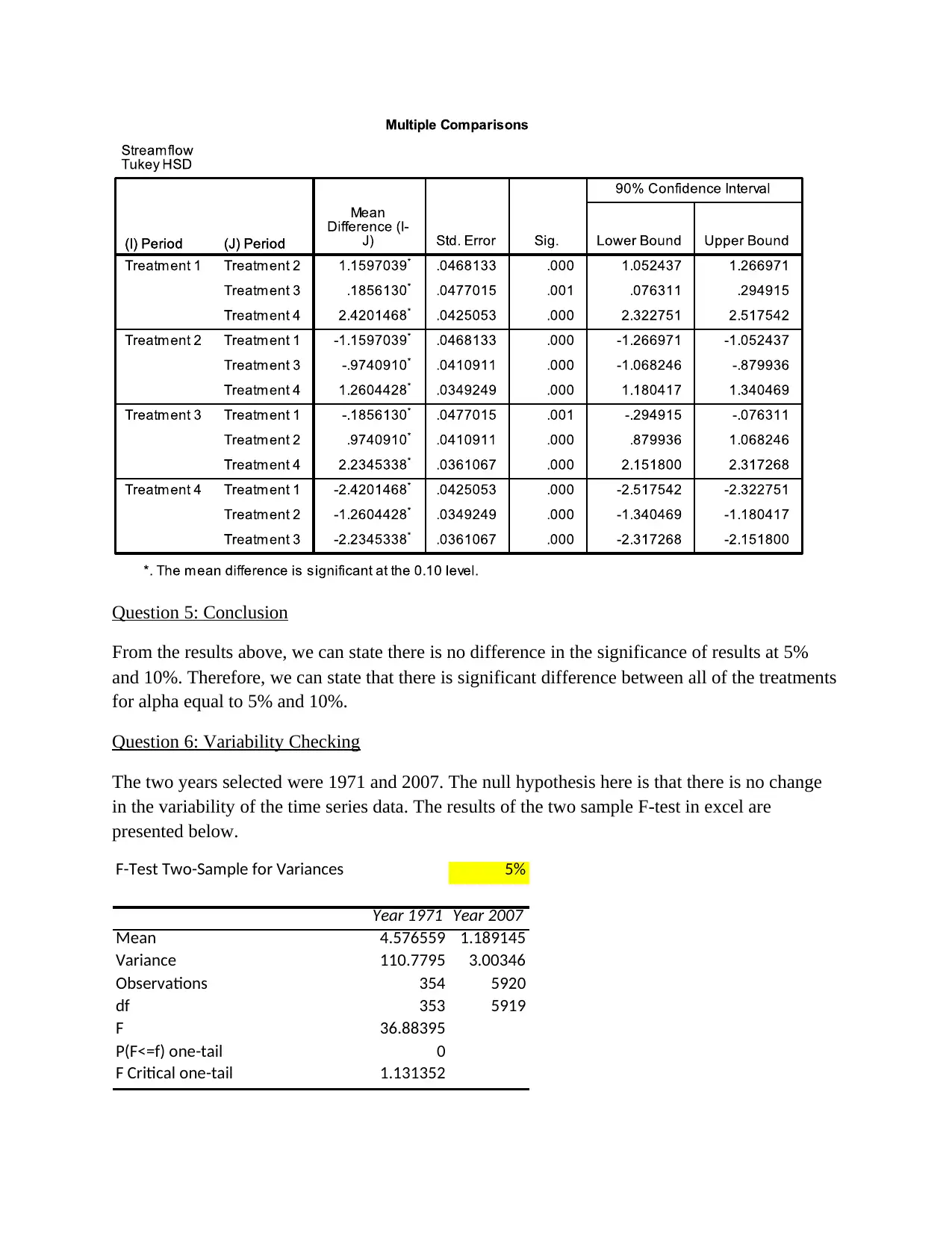
Question 5: Conclusion
From the results above, we can state there is no difference in the significance of results at 5%
and 10%. Therefore, we can state that there is significant difference between all of the treatments
for alpha equal to 5% and 10%.
Question 6: Variability Checking
The two years selected were 1971 and 2007. The null hypothesis here is that there is no change
in the variability of the time series data. The results of the two sample F-test in excel are
presented below.
F-Test Two-Sample for Variances 5%
Year 1971 Year 2007
Mean 4.576559 1.189145
Variance 110.7795 3.00346
Observations 354 5920
df 353 5919
F 36.88395
P(F<=f) one-tail 0
F Critical one-tail 1.131352
From the results above, we can state there is no difference in the significance of results at 5%
and 10%. Therefore, we can state that there is significant difference between all of the treatments
for alpha equal to 5% and 10%.
Question 6: Variability Checking
The two years selected were 1971 and 2007. The null hypothesis here is that there is no change
in the variability of the time series data. The results of the two sample F-test in excel are
presented below.
F-Test Two-Sample for Variances 5%
Year 1971 Year 2007
Mean 4.576559 1.189145
Variance 110.7795 3.00346
Observations 354 5920
df 353 5919
F 36.88395
P(F<=f) one-tail 0
F Critical one-tail 1.131352
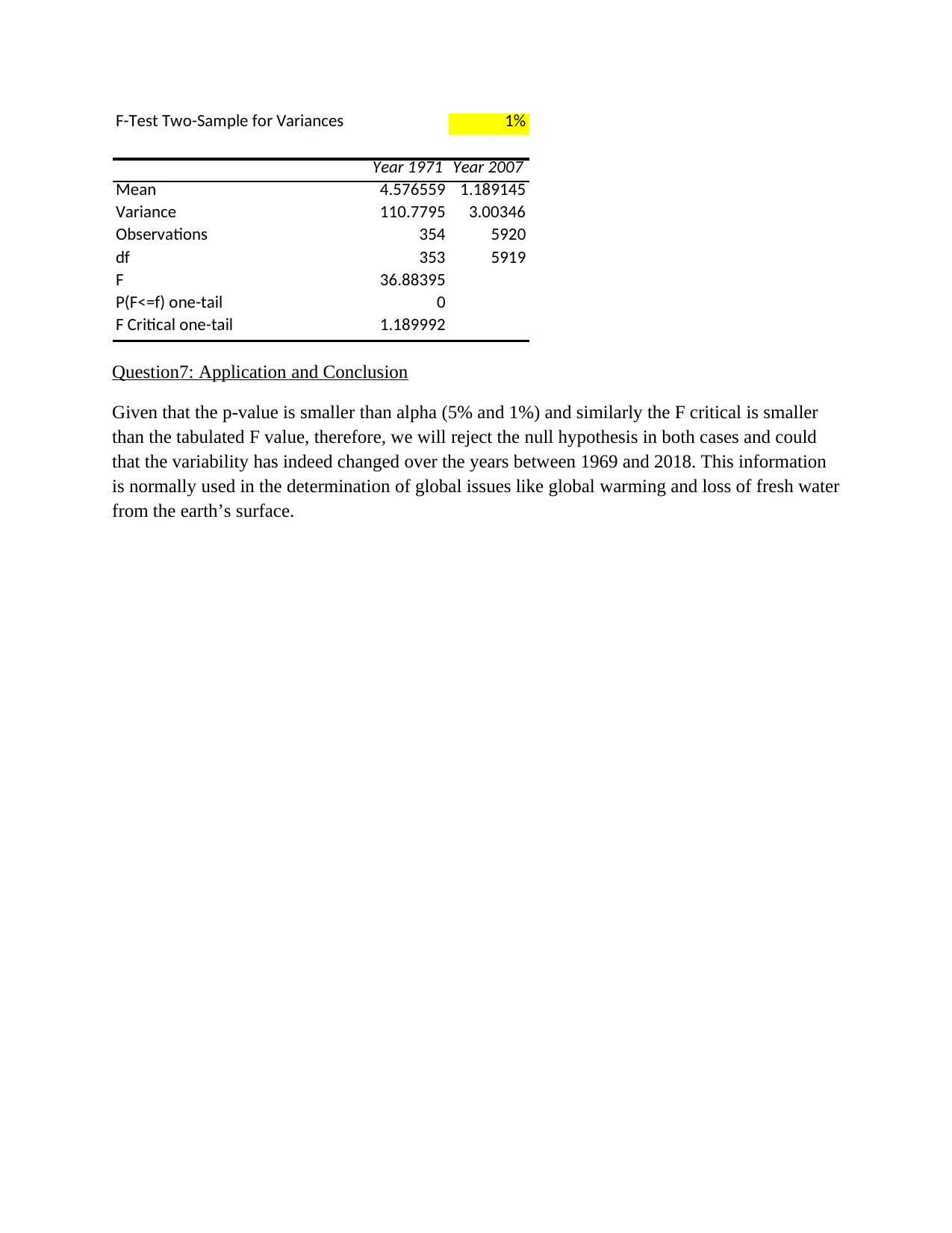
F-Test Two-Sample for Variances 1%
Year 1971 Year 2007
Mean 4.576559 1.189145
Variance 110.7795 3.00346
Observations 354 5920
df 353 5919
F 36.88395
P(F<=f) one-tail 0
F Critical one-tail 1.189992
Question7: Application and Conclusion
Given that the p-value is smaller than alpha (5% and 1%) and similarly the F critical is smaller
than the tabulated F value, therefore, we will reject the null hypothesis in both cases and could
that the variability has indeed changed over the years between 1969 and 2018. This information
is normally used in the determination of global issues like global warming and loss of fresh water
from the earth’s surface.
Year 1971 Year 2007
Mean 4.576559 1.189145
Variance 110.7795 3.00346
Observations 354 5920
df 353 5919
F 36.88395
P(F<=f) one-tail 0
F Critical one-tail 1.189992
Question7: Application and Conclusion
Given that the p-value is smaller than alpha (5% and 1%) and similarly the F critical is smaller
than the tabulated F value, therefore, we will reject the null hypothesis in both cases and could
that the variability has indeed changed over the years between 1969 and 2018. This information
is normally used in the determination of global issues like global warming and loss of fresh water
from the earth’s surface.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 9
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.




