MG 6117 - 3-Phase Power Distribution System Step-Down Transformer Lab
VerifiedAdded on 2023/06/11
|7
|1228
|363
Practical Assignment
AI Summary
This assignment focuses on the three-phase power distribution of a step-down transformer, examining star-delta and star-star connections. It includes experimental results for different load conditions (20 ohms and 10 ohms) and analyzes line/phase voltages and currents. The document also covers theoretical calculations, efficiency, regulation, turns ratio, unit impedance, and maximum fault level. The lab work involves using three single-phase transformers to form a three-phase transformer, with a design criterion for primary and secondary side connections and load configurations. The analysis includes phasor diagrams and tables of readings for each connection type.

3 power distribution of the step-down transformer∅
The three phase transformer could be formed by three single phase transformers connected to an
individual laminated core (Chunlai & Xiaoku, 2011). They have a separate magnetic circuit,
which are inter-connected so that a uniform distribution of magnetic flux could be produced
(Xinchang & Fengquan, 2010). Hence due to this type of construction they could operate at high
and low voltages and the only exception is the shell type of transformer since they are not inter-
connected. They are cost effective and the three phase winding could be seen in the figure given
below.
Figure 1: Construction of three phase transformer
Group 1:
Star- Delta connection with load 20 ohms:
In this type, the primary side is connected like a star and the secondary type is connected like a
delta (Keping, Daozhuo & Pengfei, 2012). Usually we use different symbols and alphabets to
differentiate the start and delta connections. Normally the primary side could be denoted by the
uppercase letters such as R, Y and B (the phases are differentiated by different colors especially
red, yellow and blue) and the secondary side could be indicated by the lower case alphabets.
Certain technical definitions should be known while dealing with the transformer. The Line
voltage is referred as a voltage between any line and the phase voltage is referred as the voltage
among any line and the neutral point of the transformer (Jing, Xin & Liqiang, et al., 2013). This
phase voltage is equal to 1/√3 times that of the line voltage. This could be represented as,
VP = 1/√3 VL
The three phase transformer could be formed by three single phase transformers connected to an
individual laminated core (Chunlai & Xiaoku, 2011). They have a separate magnetic circuit,
which are inter-connected so that a uniform distribution of magnetic flux could be produced
(Xinchang & Fengquan, 2010). Hence due to this type of construction they could operate at high
and low voltages and the only exception is the shell type of transformer since they are not inter-
connected. They are cost effective and the three phase winding could be seen in the figure given
below.
Figure 1: Construction of three phase transformer
Group 1:
Star- Delta connection with load 20 ohms:
In this type, the primary side is connected like a star and the secondary type is connected like a
delta (Keping, Daozhuo & Pengfei, 2012). Usually we use different symbols and alphabets to
differentiate the start and delta connections. Normally the primary side could be denoted by the
uppercase letters such as R, Y and B (the phases are differentiated by different colors especially
red, yellow and blue) and the secondary side could be indicated by the lower case alphabets.
Certain technical definitions should be known while dealing with the transformer. The Line
voltage is referred as a voltage between any line and the phase voltage is referred as the voltage
among any line and the neutral point of the transformer (Jing, Xin & Liqiang, et al., 2013). This
phase voltage is equal to 1/√3 times that of the line voltage. This could be represented as,
VP = 1/√3 VL
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Every relevant secondary winding will have the same voltage induced in it. Since the secondary
windings are delta connected, the line voltage will be 1/√3 VL.
The Turns ratio could be represented as the ratio between the primary winding NP and the
secondary winding NS. This could be denoted by the following equation
Turns ratio (n) = NP / NS
For the star- delta connection this could be written as,
Turns ratio (n) = VP /√3 VL
If the transformer is provided with the same number of windings in the primary and the
secondary winding of 1:1 ratio then √3:1 is the step-down line voltage ratio. The line voltage will
VL = n VL / √3 and the line current will be IL = √3. IL /n. the transformation ration (K) is defined
as the ratio between the secondary phase voltage and the primary phase voltage (Lin, Yi & Ke, et
al., 2012). Since the primary side is star connected, we could need only few numbers of turns.
This could be used efficiently for the high voltage step-down transformers. The impedance of
each phase could be calculated by Zp = . The connection between primary and
secondary winding and the phasor diagram connection is shown in the figure given below.
Figure 2: Transformer connection – star-delta network
windings are delta connected, the line voltage will be 1/√3 VL.
The Turns ratio could be represented as the ratio between the primary winding NP and the
secondary winding NS. This could be denoted by the following equation
Turns ratio (n) = NP / NS
For the star- delta connection this could be written as,
Turns ratio (n) = VP /√3 VL
If the transformer is provided with the same number of windings in the primary and the
secondary winding of 1:1 ratio then √3:1 is the step-down line voltage ratio. The line voltage will
VL = n VL / √3 and the line current will be IL = √3. IL /n. the transformation ration (K) is defined
as the ratio between the secondary phase voltage and the primary phase voltage (Lin, Yi & Ke, et
al., 2012). Since the primary side is star connected, we could need only few numbers of turns.
This could be used efficiently for the high voltage step-down transformers. The impedance of
each phase could be calculated by Zp = . The connection between primary and
secondary winding and the phasor diagram connection is shown in the figure given below.
Figure 2: Transformer connection – star-delta network
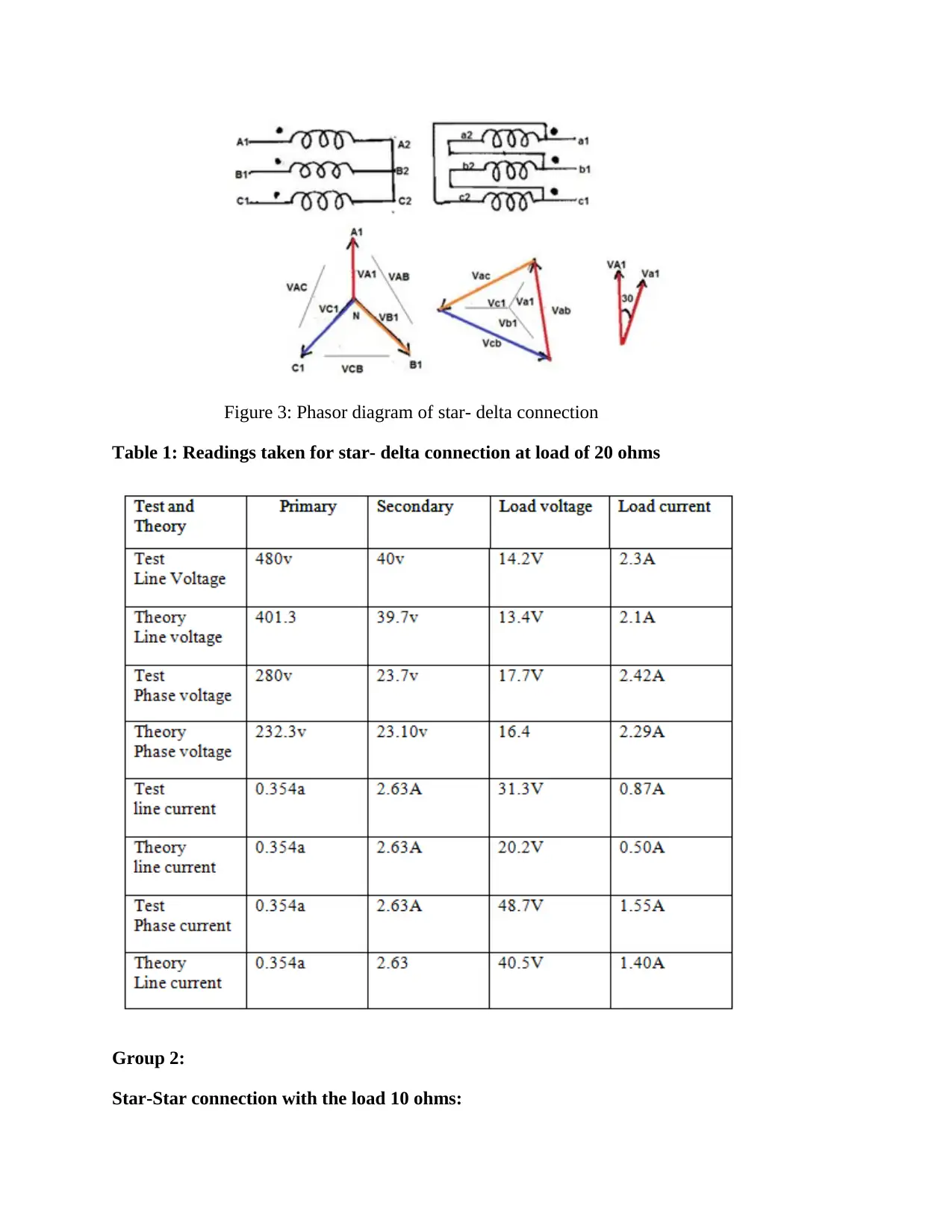
Figure 3: Phasor diagram of star- delta connection
Table 1: Readings taken for star- delta connection at load of 20 ohms
Group 2:
Star-Star connection with the load 10 ohms:
Table 1: Readings taken for star- delta connection at load of 20 ohms
Group 2:
Star-Star connection with the load 10 ohms:
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

In this type both the primary and the secondary sides are connected in the star with the phase
angle of 120 degrees that is out of phase with the rest two phases. The primary winding is
magnetically linked with the other secondary winding with the common core leg. In this
connection the windings are terminated to a neutral connection point. This neutral part could be
grounded or not grounded based on the required specification (Lin, Yi & Ke, et al. (2012).
Although the exciting voltage is sinusoidal, the magnetizing current of the transformer is not
purely sinusoidal, since they have sufficient amount of odd harmonic component. Suppose when
the identical transformers are connected, which is energized by a particular frequency of equal
magnitude voltage level (say 60 Hz), the current could be revoked at the neutral. This is because
the vector sum of the current could be zero due to their phase angle held at 120 degrees.
Anyways the third, sixth and so on harmonics tends to remain in-phase and hence they won’t
cancel out each other. These are said to be known as the zero harmonics. In this situation we tend
to have a neutral current. The B-H curve of the star-star connection is said to be non-linear. This
could lead to the situation of sinusoidal induced voltages to be supported by odd-harmonics
magnetizing currents.
Due to the star connection we have lesser turns for windings in which phase voltage are 1/√3
times the line voltage. The phase current is same as the line current due to the star connection,
i.e., IP = IL. The phasor diagram of the star-star connection is shown in the figure given below
Figure 4: Phasor diagram of star-star connection
angle of 120 degrees that is out of phase with the rest two phases. The primary winding is
magnetically linked with the other secondary winding with the common core leg. In this
connection the windings are terminated to a neutral connection point. This neutral part could be
grounded or not grounded based on the required specification (Lin, Yi & Ke, et al. (2012).
Although the exciting voltage is sinusoidal, the magnetizing current of the transformer is not
purely sinusoidal, since they have sufficient amount of odd harmonic component. Suppose when
the identical transformers are connected, which is energized by a particular frequency of equal
magnitude voltage level (say 60 Hz), the current could be revoked at the neutral. This is because
the vector sum of the current could be zero due to their phase angle held at 120 degrees.
Anyways the third, sixth and so on harmonics tends to remain in-phase and hence they won’t
cancel out each other. These are said to be known as the zero harmonics. In this situation we tend
to have a neutral current. The B-H curve of the star-star connection is said to be non-linear. This
could lead to the situation of sinusoidal induced voltages to be supported by odd-harmonics
magnetizing currents.
Due to the star connection we have lesser turns for windings in which phase voltage are 1/√3
times the line voltage. The phase current is same as the line current due to the star connection,
i.e., IP = IL. The phasor diagram of the star-star connection is shown in the figure given below
Figure 4: Phasor diagram of star-star connection
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
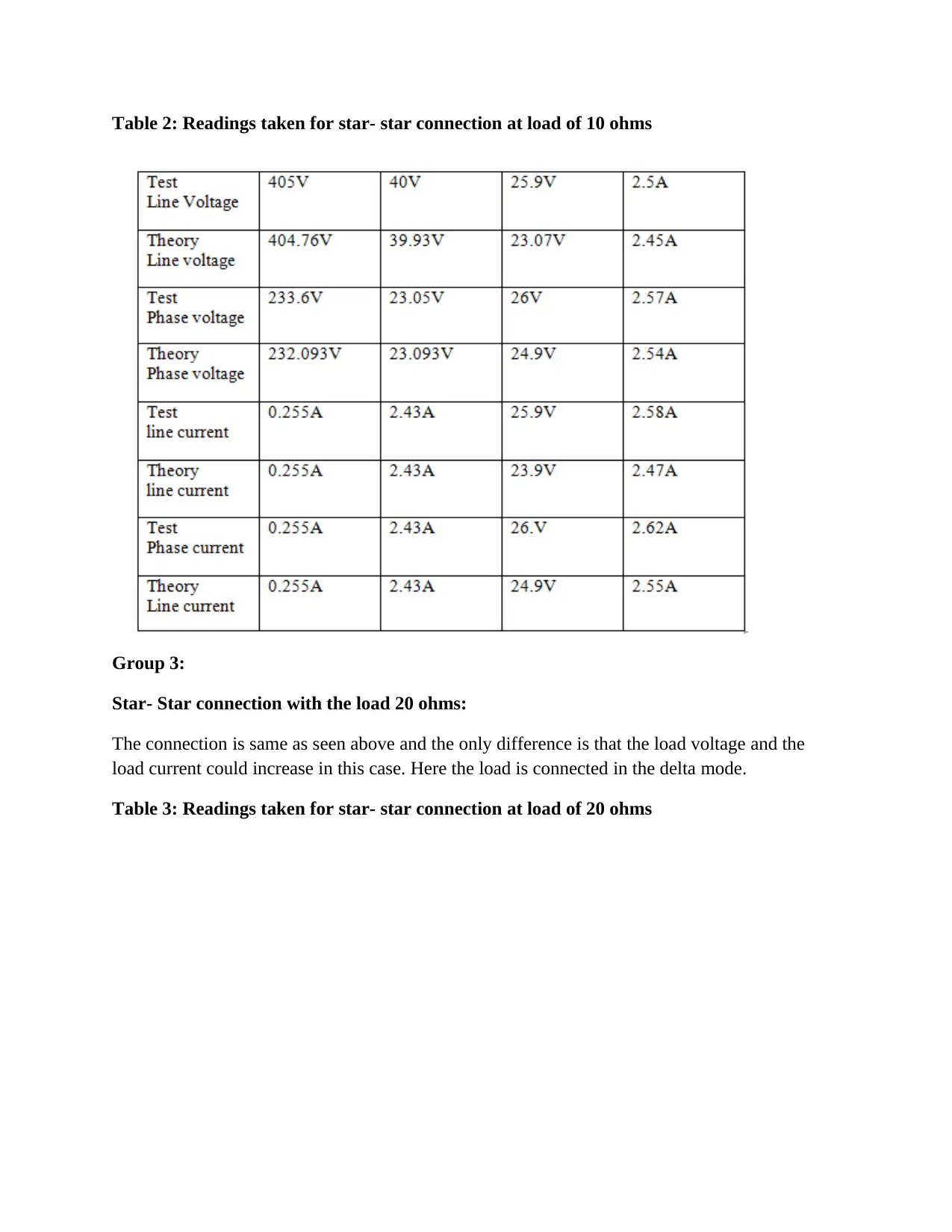
Table 2: Readings taken for star- star connection at load of 10 ohms
Group 3:
Star- Star connection with the load 20 ohms:
The connection is same as seen above and the only difference is that the load voltage and the
load current could increase in this case. Here the load is connected in the delta mode.
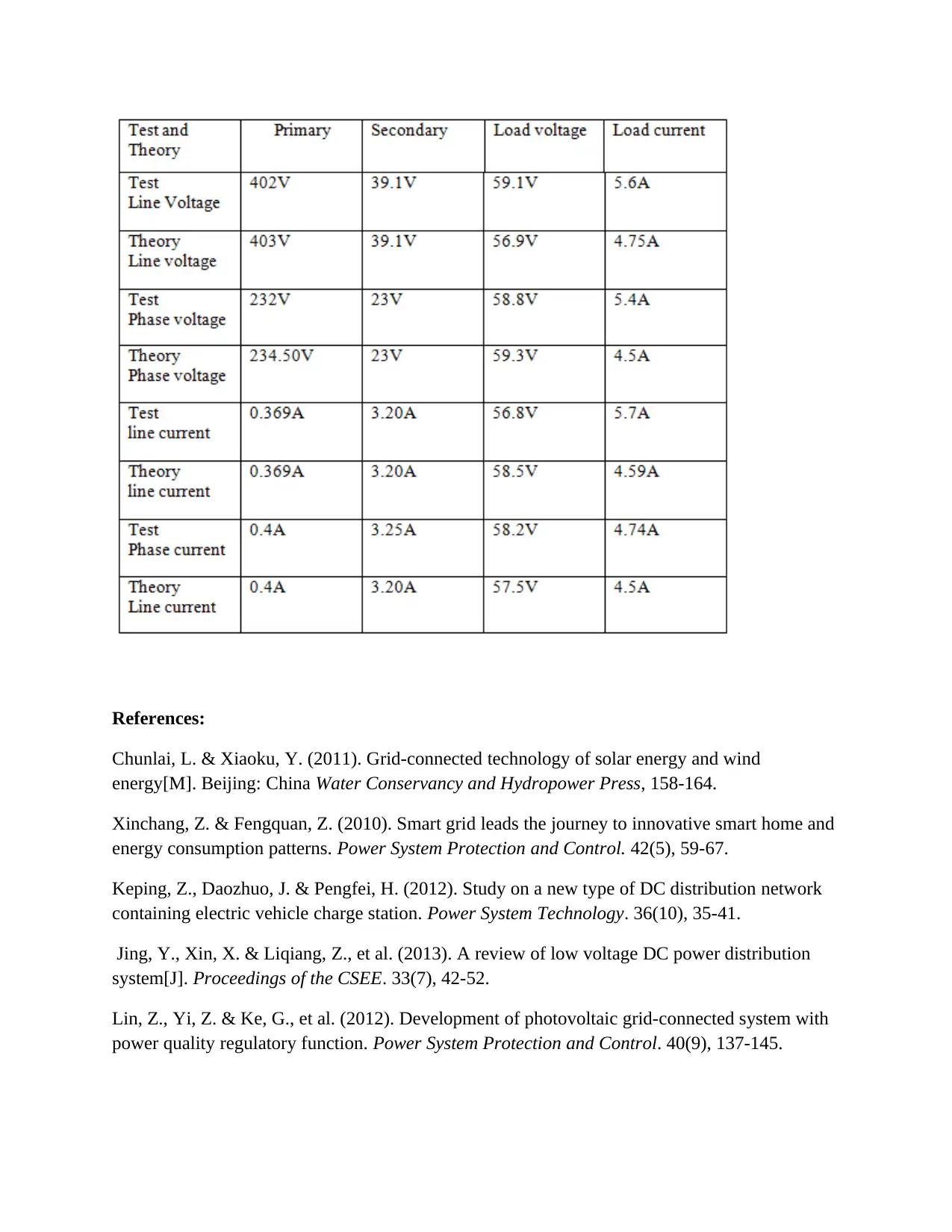
Table 3: Readings taken for star- star connection at load of 20 ohms
Group 3:
Star- Star connection with the load 20 ohms:
The connection is same as seen above and the only difference is that the load voltage and the
load current could increase in this case. Here the load is connected in the delta mode.
Table 3: Readings taken for star- star connection at load of 20 ohms
References:
Chunlai, L. & Xiaoku, Y. (2011). Grid-connected technology of solar energy and wind
energy[M]. Beijing: China Water Conservancy and Hydropower Press, 158-164.
Xinchang, Z. & Fengquan, Z. (2010). Smart grid leads the journey to innovative smart home and
energy consumption patterns. Power System Protection and Control. 42(5), 59-67.
Keping, Z., Daozhuo, J. & Pengfei, H. (2012). Study on a new type of DC distribution network
containing electric vehicle charge station. Power System Technology. 36(10), 35-41.
Jing, Y., Xin, X. & Liqiang, Z., et al. (2013). A review of low voltage DC power distribution
system[J]. Proceedings of the CSEE. 33(7), 42-52.
Lin, Z., Yi, Z. & Ke, G., et al. (2012). Development of photovoltaic grid-connected system with
power quality regulatory function. Power System Protection and Control. 40(9), 137-145.
Chunlai, L. & Xiaoku, Y. (2011). Grid-connected technology of solar energy and wind
energy[M]. Beijing: China Water Conservancy and Hydropower Press, 158-164.
Xinchang, Z. & Fengquan, Z. (2010). Smart grid leads the journey to innovative smart home and
energy consumption patterns. Power System Protection and Control. 42(5), 59-67.
Keping, Z., Daozhuo, J. & Pengfei, H. (2012). Study on a new type of DC distribution network
containing electric vehicle charge station. Power System Technology. 36(10), 35-41.
Jing, Y., Xin, X. & Liqiang, Z., et al. (2013). A review of low voltage DC power distribution
system[J]. Proceedings of the CSEE. 33(7), 42-52.
Lin, Z., Yi, Z. & Ke, G., et al. (2012). Development of photovoltaic grid-connected system with
power quality regulatory function. Power System Protection and Control. 40(9), 137-145.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Haifeng, L., Yanchuang, F. & Zixing, L., et al. (2013). Research on low voltage ride through of
photovoltaic plant based on deadbeat control[J]. Power System Protection and Control. 41(21),
110-115.
photovoltaic plant based on deadbeat control[J]. Power System Protection and Control. 41(21),
110-115.
1 out of 7
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.




