Civil Engineering Materials D28MA: Metallic Beam Bending Lab Report

This laboratory report details a 1-point beam bending experiment conducted to determine the flexural stiffness of steel, brass, and aluminum. The experiment involved placing metallic beam samples on supports and applying a load in the mid-span while measuring displacement. The report ...Read More

Introduction:
We are currently producing about 800 million tonnes of steel worldwide for a variety of uses and
about 40% of this production originates from recycled steel. Steel is possibly the most versatile
construction material - it is strong in tension and in compression, it is easily formable and has
uniform quality. The inclusion of steel in concrete to produce reinforced concrete has extended its
versatility.
Objective:
The purpose of this laboratory is to use a 1-point beam bending test in order to determine the
flexural stiffness of different metallic materials; steel, copper, brass and aluminium, specific
objectives are:
 Awareness of safety in the laboratory
 Understand the different metallic materials behaviour
 Perform an experimental test to determine the flexural behaviour of the metallic materials
 To use the standard beam bending equations to back calculate the metallic flexural Young’s
Modulus.
 Analyse and interpret data against typical values for steel
 Enhance ability to work in teams and communicate
 To gain experience of the process of experimental materials testing
 To gain experience of working in a laboratory environment
Procedure:
Figure 1 shows the experimental setup. Essentially a particular metallic beam sample has been
placed on two supports and is to be loaded in the mid-span as shown in Figure 2.

Questions:
(1) Draw the beam’s cross-section below and, without disturbing the beam, measure the
dimensions and thickness of the specimen.
Steel Brass Aluminium
b=20.8mm b=20.8mm b=20.8mm
d=4mm d=4mm d=4mm
L=510mm L=510mm L=510mm
(2) What is the distance of the neutral axis from the beam’s upper surface?
Since the object is uniform about the x axis and y axis. So, the neutral axis will be passing through the
centre of gravity of the object. So, the distance of the neutral axis from the beam’s upper surface is d/2. And
that will be 2 mm.

Since the section of the all the material are same the distance between neutral axis and upper surface is also
same for the all section.
(3) Determine the 2nd moment of area of the cross-section along the beam’s neutral axis?
Here beam’s neutral axis is at the geometric centroid of the cross-section so,
The equation for finding the 2nd moment of inertia along the beam’s neutral axis is
I = b d3
12
Now put the value of cross section in this equation.
I =(20.8)(4)3
12
I = 1331.2
12
I =110.933 mm4
Since the cross section of the all the material are same 2nd moment of inertia is also same.
(4) Carefully add weights to the beam at the places indicated on the beams upper surface. After
each increment record the number indicated on the dial gauge and convert to displacement
as appropriate in Table 1.
Table 1: Experimental Data Steel
Increment Number Weight Added Per Position
(N)
Displacement (mm)
1 100 g 5 mm
2 500 g 46 mm
3 1000 g 90 mm
4 1900 g 177 mm
Table 2: Experimental Data Brass
Increment Number Weight Added Per Position (N) Displacement (mm)
1 100 g 1 mm
2 500 g 28 mm
3 1000 g 66 mm
4 1900 g 126 mm
Table 3: Experimental Data Aluminium
Increment Number Weight Added Per Position
(N)
Displacement (mm)
1 100 g 10 mm
2 500 g 62 mm
3 1000 g 130 mm
4 1900 g 246 mm

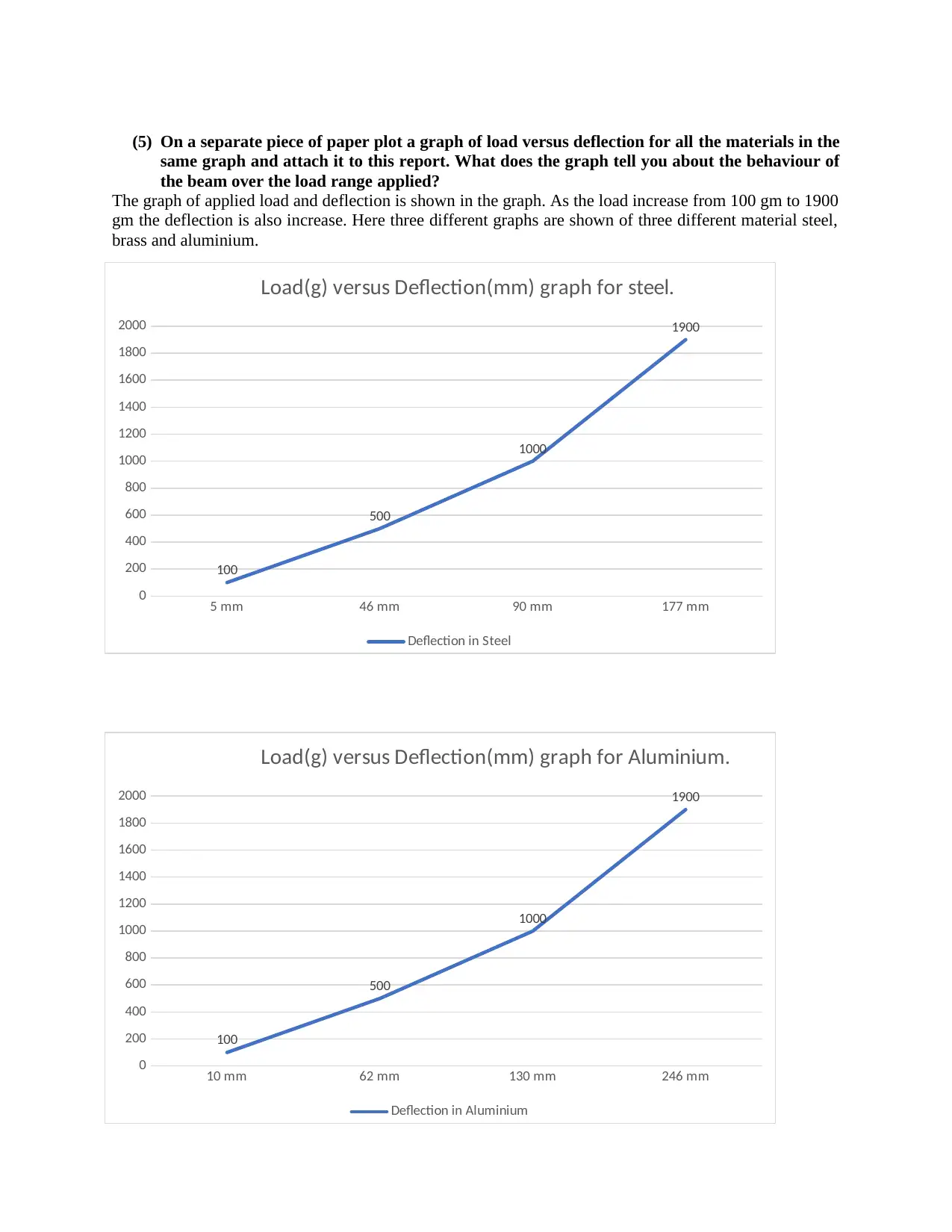
(5) On a separate piece of paper plot a graph of load versus deflection for all the materials in the
same graph and attach it to this report. What does the graph tell you about the behaviour of
the beam over the load range applied?
The graph of applied load and deflection is shown in the graph. As the load increase from 100 gm to 1900
gm the deflection is also increase. Here three different graphs are shown of three different material steel,
brass and aluminium.
5 mm 46 mm 90 mm 177 mm
0
200
400
600
800
1000
1200
1400
1600
1800
2000
100
500
1000
1900
Load(g) versus Deflection(mm) graph for steel.
Deflection in Steel
10 mm 62 mm 130 mm 246 mm
0
200
400
600
800
1000
1200
1400
1600
1800
2000
100
500
1000
1900
Load(g) versus Deflection(mm) graph for Aluminium.
Deflection in Aluminium

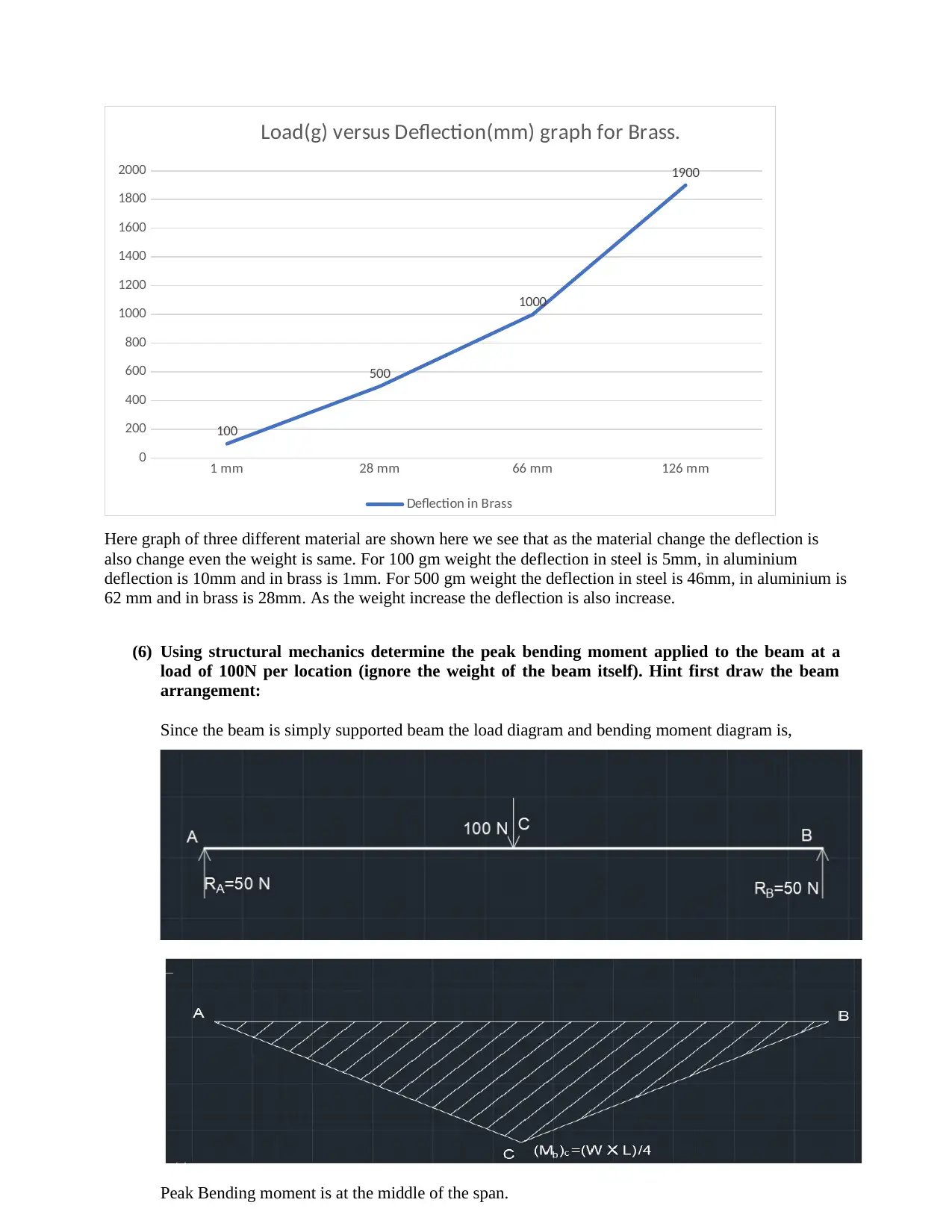
1 mm 28 mm 66 mm 126 mm
0
200
400
600
800
1000
1200
1400
1600
1800
2000
100
500
1000
1900
Load(g) versus Deflection(mm) graph for Brass.
Deflection in Brass
Here graph of three different material are shown here we see that as the material change the deflection is
also change even the weight is same. For 100 gm weight the deflection in steel is 5mm, in aluminium
deflection is 10mm and in brass is 1mm. For 500 gm weight the deflection in steel is 46mm, in aluminium is
62 mm and in brass is 28mm. As the weight increase the deflection is also increase.
(6) Using structural mechanics determine the peak bending moment applied to the beam at a
load of 100N per location (ignore the weight of the beam itself). Hint first draw the beam
arrangement:
Since the beam is simply supported beam the load diagram and bending moment diagram is,
Peak Bending moment is at the middle of the span.

Equation for finding the maximum bending moment is ¿ ( point load)(length of the beam)
4
So, the maximum bending moment at c is¿ (100)(510)
4
(Mb)c=12750 N.m
(7) Using the following 1-point beam bending equation estimate the flexural stiffness (Young’s
Modulus) of the beam at the load given in (6) above (i.e. at the appropriate displacement):
P = load, l = length, E = flexural modulus, I = 2nd moment of area about the neutral axis
Flexural Young’s Modulus of Steel = 18 x 104 N/mm2
Flexural Young’s Modulus of Brass = 11 x 104 N/mm2
Flexural Young’s Modulus of Aluminium = 6.9 x 104 N/mm2
Here, we have to find the Stiffness of the beam for the equation to find the stiffness is,
stiffness(K)= Load ( P)
Deflection(δ ).
In our case, P=100N
We have the equation δ= P l3
48 EI
Now put these two values in main equation we got,
K= 48 EI
l3
Ksteel= 48 x 18 x 104 x 110.93
5103 = 7.2252 N/mm.
Kbrass= 48 x 11 x 104 x 110.93
5103 = 4.4154 N/mm.
Kaluminium = 48 x 6.9 x 104 x 110.93
5103 =2.7696 N/mm.
(8) Would the flexural Young’s modulus be different to the Tensile Young’s Modulus?
Briefly justify your answer
Young’s modulus is the elasticity of the material, which is the relation between the deformation of a
material and power needed to deform it. Normally the young’s modulus is denoted by E. Where,
Tensile modulus is the ratio of stress to strain and is equal to the slope of the stress-strain diagram for the
material.

(9) Using the following equation determine the peak elastic normal stress on the outer fibres of
the beam for the load given in (6) above:
M
I = σ x
y
Where, M= Peak Bending Moment.
I = Moment of inertia
σ x= Tensile Stress
y=Depth of neutral axis
Now put the value of the M, I, y
Tensile stressσ x= M × y
I
σ x= 12750× 2
110.93
σ x=229.87 N /mm2
(10) Using a standard value for the Young’s Modulus of mild steel estimate the stiffness
ratio of the brass and aluminium to the mild steel, i.e. stiffness ratio=copper/steel.
In problem no. 7 we find the stiffness of steel, brass and aluminium. In this problem we have to
find the ratio of the two stiffness.
Stiffness ratio(brass/steel) =4.4154/7.2252= 0.6111
Stiffness ration (aluminium/steel) = 2.7696/7.2252 =0.3833
(11) What does this stiffness ratio tell you about the probable deformation behaviour of a
structure built from the copper, brass and aluminium when compared to one built of steel
when the same live load is added to the structure?
Stiffness of beam define as the ratio between the applied force and deflection. In simple word we can say
that load required for unit displacement is called stiffness. If the more load is required for unit
displacement the material will be affirmative. And if less load required for unit displacement is called stiff
material. So, the ratio of different material to the steel shows the comparison of deflection with respect to
steel.
References:
1). Dr. R.K.Bansal, Third Edision1996, A Text Book of Strength of Material, Laxmi Publication.
2). R.S.Khurmi and N.Khurmi, 2010, Strength Of Material(Mechanics Of Solid), S.Chand Publication.
3). Other link References:
https://www.google.com/search?

q=stiffness&rlz=1C1CHBF_enIN849IN849&oq=stiffness&aqs=chrome.0.0l8.1991j0j8&sourceid=chrome&i
e=UTF-8