MATH 230 Take-Home Final Examination: Statistical Reasoning
VerifiedAdded on 2022/09/06
|8
|852
|16
Homework Assignment
AI Summary
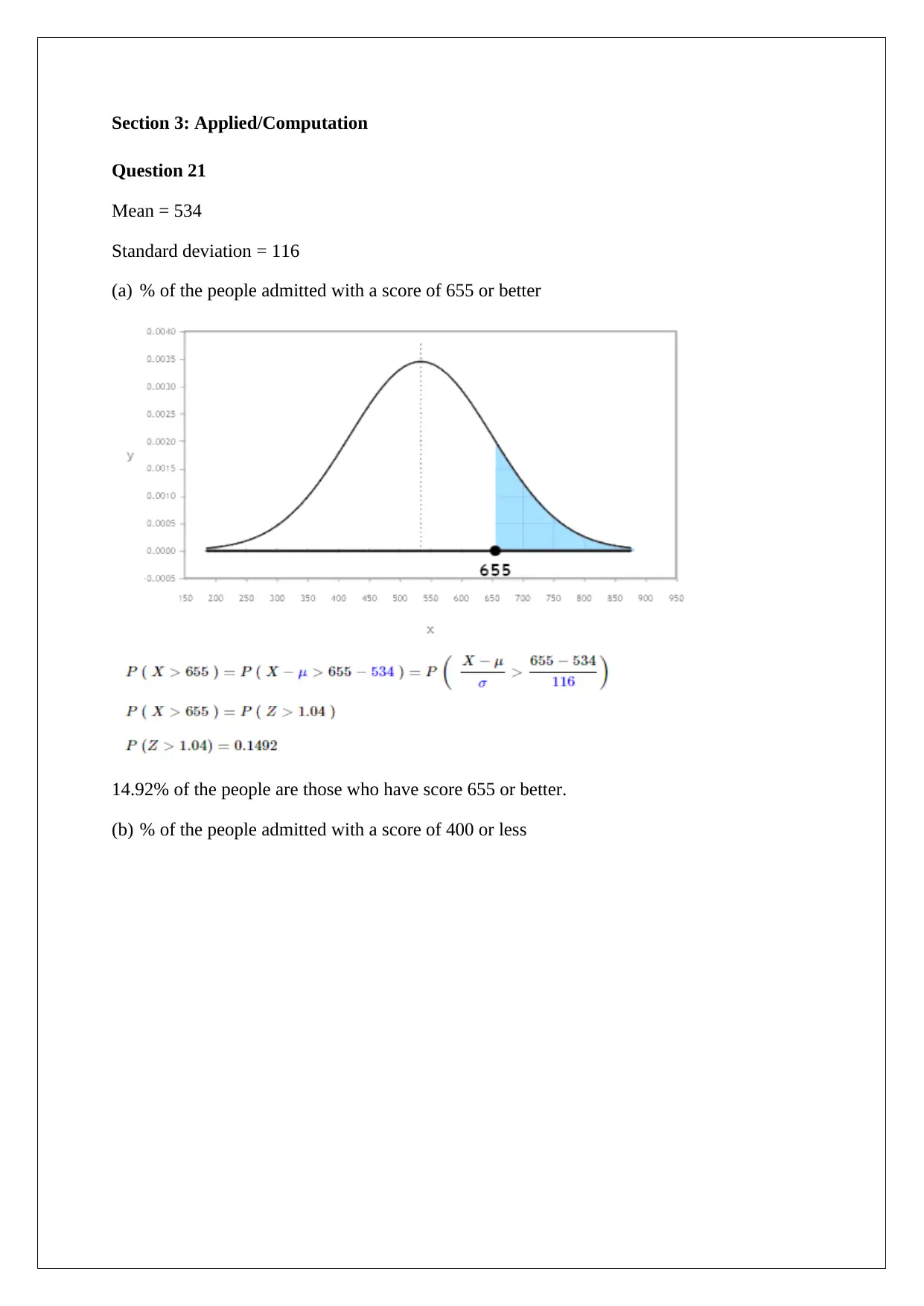
This document provides a comprehensive solution to a MATH 230 take-home final examination in Introduction to Statistical Reasoning and Analysis. The exam is divided into three sections: multiple-choice questions, true/false questions, and applied/computation questions. The solution includes answers to multiple-choice questions, true/false statements, and detailed solutions to applied problems involving mean, standard deviation, hypothesis testing, confidence intervals, and the central limit theorem. The applied questions cover topics such as calculating probabilities, determining z-values, and interpreting statistical results. The document also addresses the student's key takeaways from the course, emphasizing the importance of inferential statistical techniques and the central limit theorem in real-life applications. The solution demonstrates the application of statistical concepts to real-world scenarios, providing a valuable resource for students studying statistics.
1 out of 8














![[object Object]](/_next/static/media/star-bottom.7253800d.svg)