Assessment Task 2: Simple & Multiple Linear Regression Analysis Report
VerifiedAdded on 2022/09/14
|6
|807
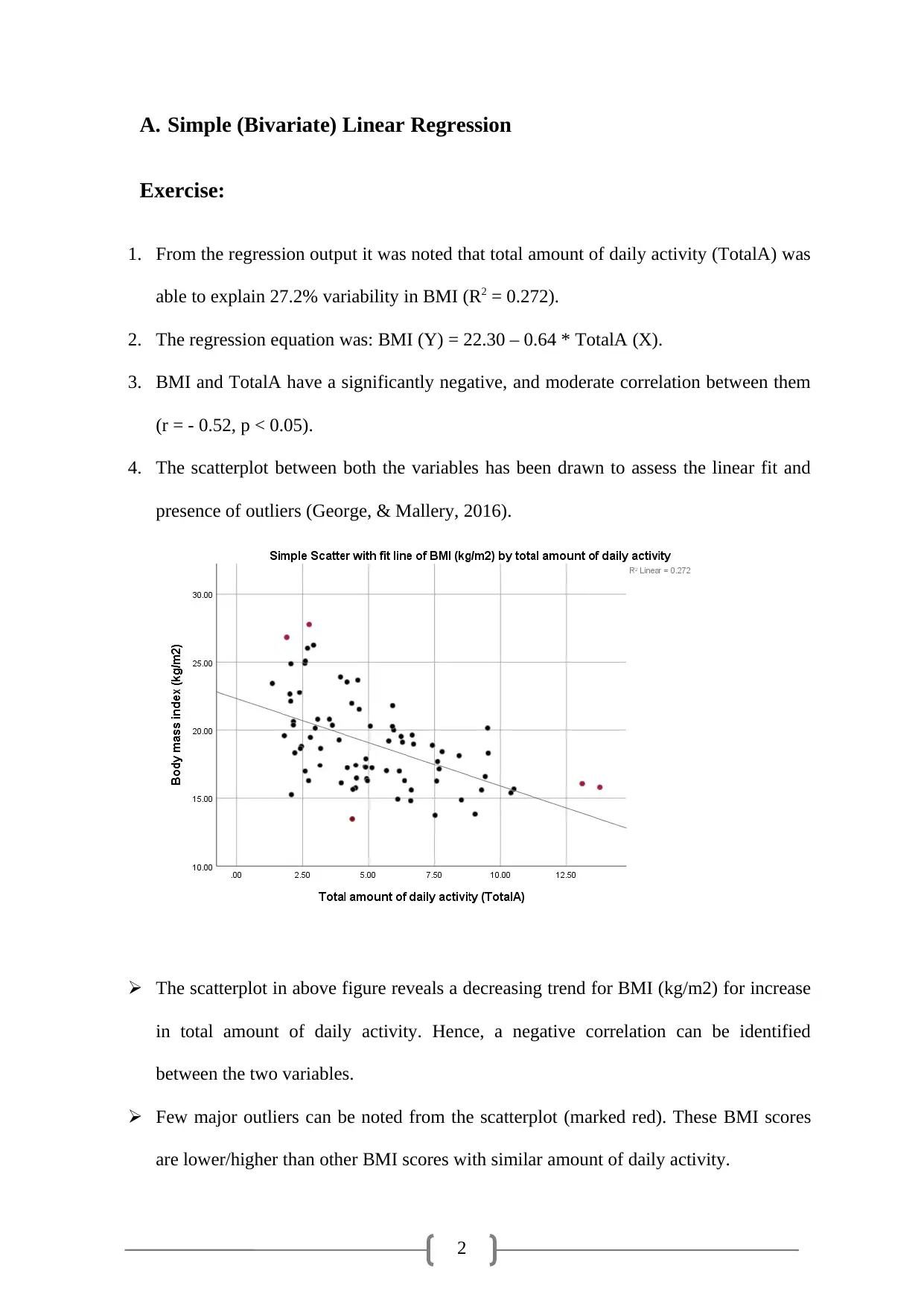
|16
Practical Assignment
AI Summary
This assignment presents a detailed analysis of simple and multiple linear regression models using statistical techniques. The student conducted a simple linear regression to assess the relationship between total daily activity (TotalA) and Body Mass Index (BMI), finding a negative correlation and explaining 27.2% of the variance in BMI. The analysis then extends to multiple linear regression, comparing stepwise and enter methods. Two models were developed: one with TotalA alone and another with Age and TotalA. The stepwise model incorporated TotalA and then Age, explaining 31.0% of the BMI variation. The enter method, including Age, Gender, and TotalA, explained 32.8% of the variance. The student evaluated the models, highlighting the significance of predictors, multicollinearity, and heteroscedasticity, concluding the stepwise model was more appropriate. The assignment includes regression equations, statistical outputs, and references to relevant literature.
1 out of 6




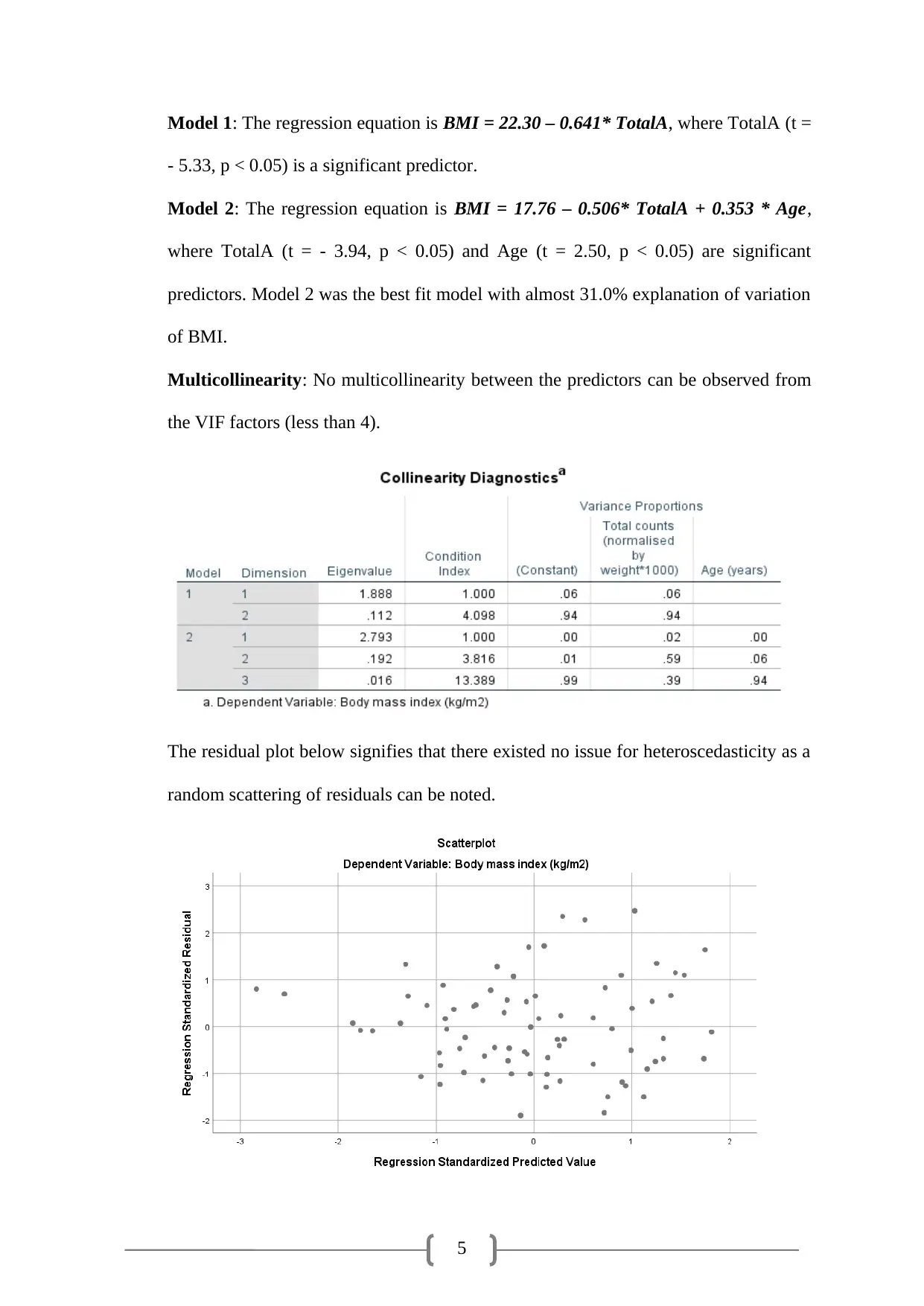







![[object Object]](/_next/static/media/star-bottom.7253800d.svg)