Calculus I (UN1101) Exercise Sheet 12: Integrals and Area Calculations

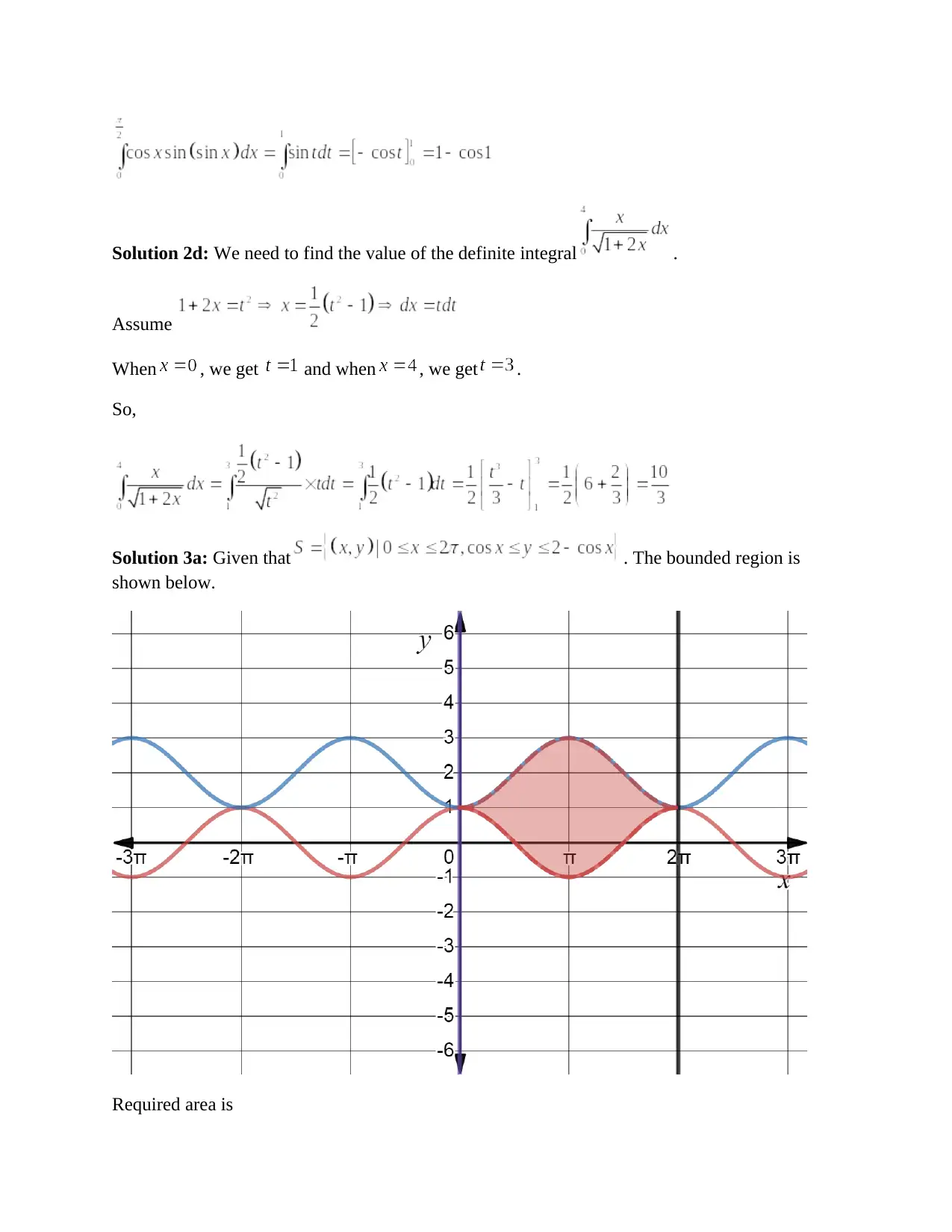
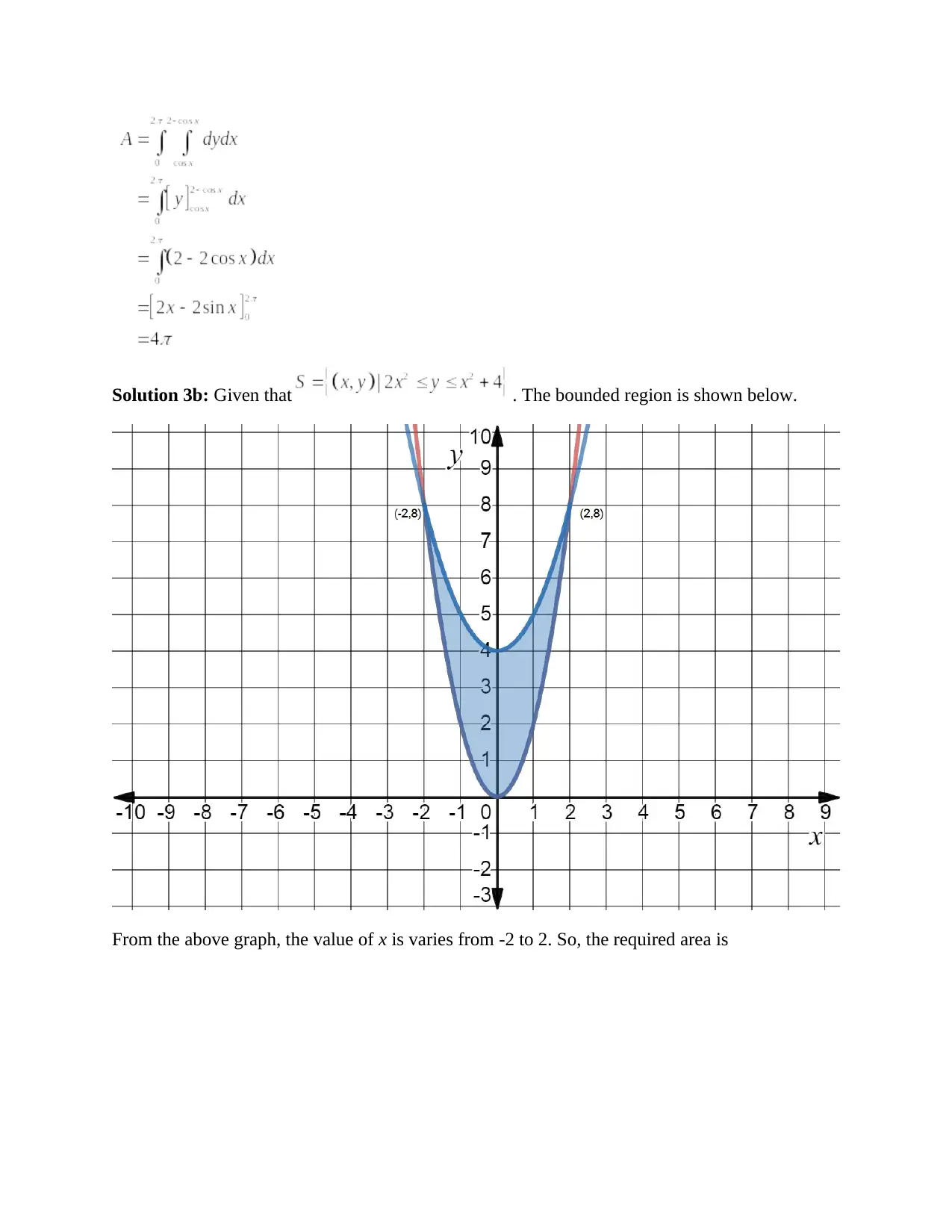
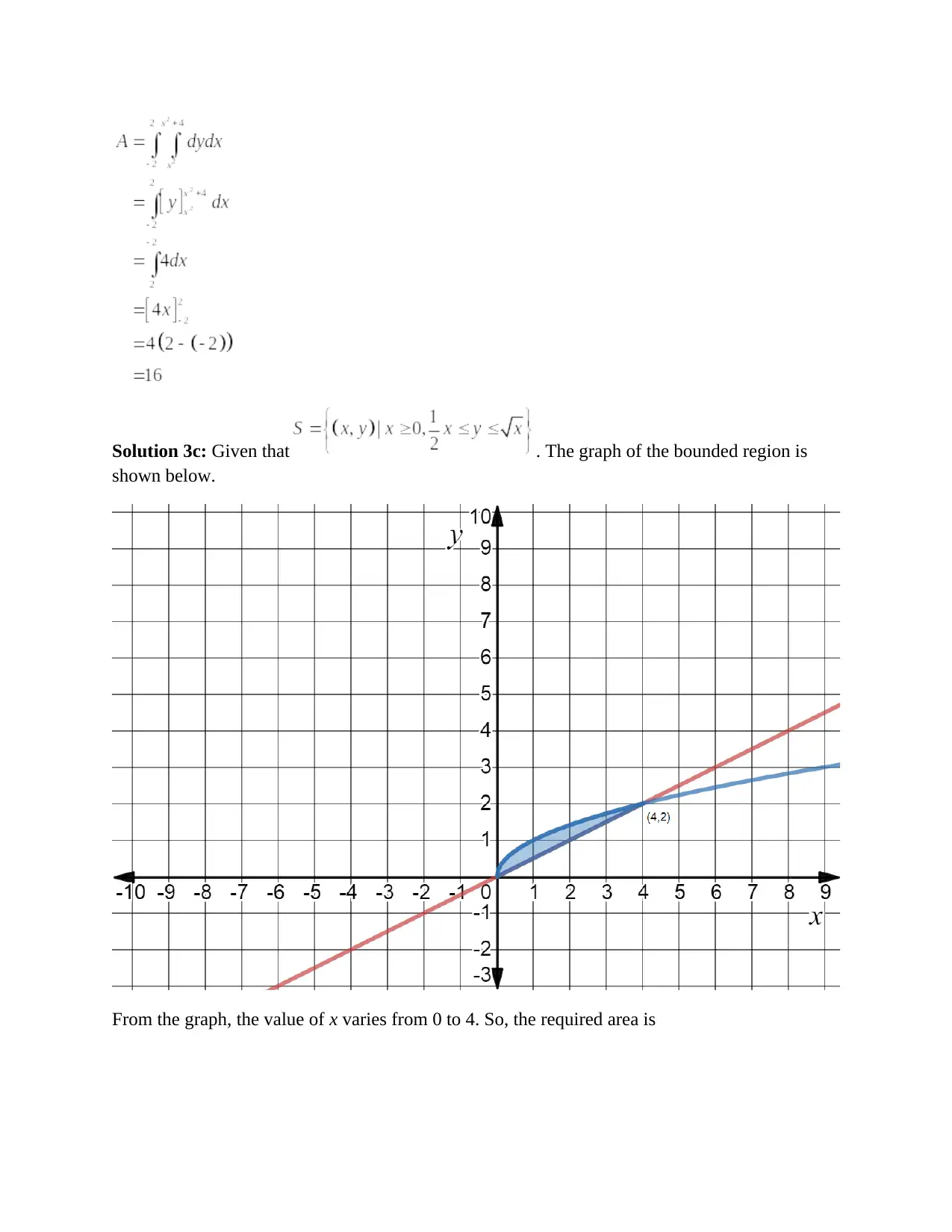
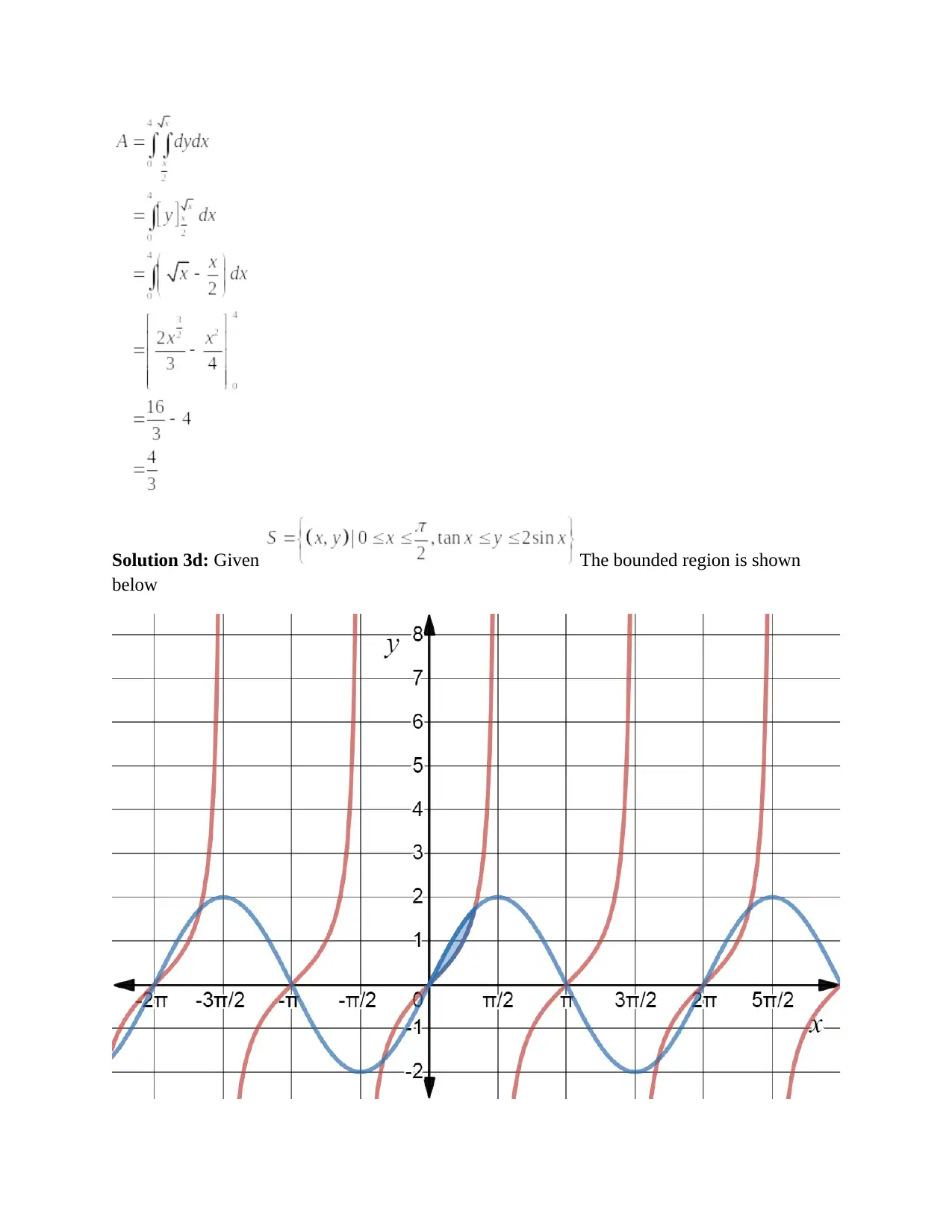
This document contains the solutions to Calculus I Exercise Sheet 12, focusing on integral calculus. The solutions cover a range of problems including computing indefinite integrals of various functions such as polynomials, trigonometric functions, and expressions involving radicals. The solutions also include the computation of definite integrals, applying the fundamental theorem of calculus, and evaluating the definite integrals within given limits. Furthermore, the document provides solutions for finding the area of regions bounded by curves, requiring the use of definite integrals to calculate the area between curves and the x-axis. The solutions are presented step-by-step, demonstrating the application of integration techniques and providing clear explanations for each step of the problem-solving process.

Solution 1a: We need to find the value of the integral .
Suppose that . So,
, Where C is the constant of integration.
Solution 1b: We need to find the value of the integral .
Suppose that . So,
, Where C is the constant of
integration.
Solution 1c: We need to find the value of the integral .
Suppose that . So,
, Where C is the constant of
integration.
Solution 1d: We need to find the value of the integral .
Suppose that . So,
, Where C is the constant of integration.
Solution 1e: We need to find the value of the integral .
Suppose that . So,

Where C is the constant of integration.
Solution 1f: We need to find the value of the integral .
Suppose that . So,
, Where C is the constant of integration.
Solution 1g: We need to find the value of the integral .
Suppose that . So,
…. (1)
Now, suppose that , so

Where C is the constant of integration.
Solution 1h: We need to find the value of the integral .
Suppose that . So,
Where C is the constant of integration.
Solution 1i: We need to find the value of the integral .
Suppose that . So,

Where C is the constant of integration.
Solution 2a: We need to find the value of the definite integral .
Solution 2b: We need to find the value of the definite integral .
Solution 2c: We need to find the value of the definite integral .
Assume that
When , we get and when , we get .
So,

Solution 2d: We need to find the value of the definite integral .
Assume
When , we get and when , we get .
So,
Solution 3a: Given that . The bounded region is
shown below.
Required area is

Solution 3b: Given that . The bounded region is shown below.
From the above graph, the value of x is varies from -2 to 2. So, the required area is

Solution 3c: Given that . The graph of the bounded region is
shown below.
From the graph, the value of x varies from 0 to 4. So, the required area is

Solution 3d: Given The bounded region is shown
below

From the graph, the value of x varies from 0 to . So,
The required area is