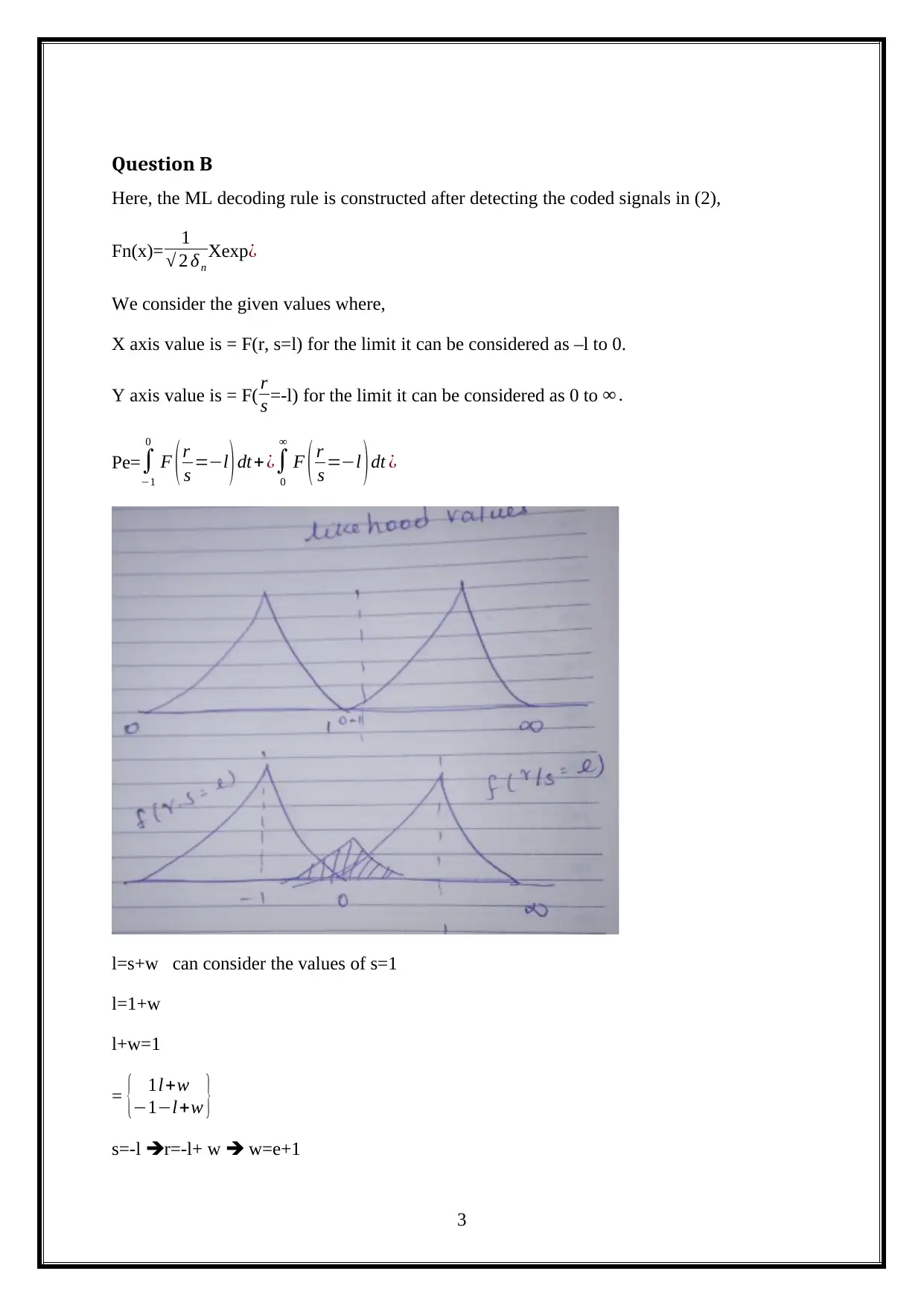
Bit Error Probability, ML Decoding Rule and Specific Codeword Decoding

This document covers topics like Bit Error Probability, ML Decoding Rule and Specific Codeword Decoding in Electronics. It explains the formulas and calculations involved in these topics. The document also mentions the subject, course code and college/university.

Electronics

Table of Contents
Task 1.........................................................................................................................................1
Question A.............................................................................................................................1
Question B..............................................................................................................................2
Question C..............................................................................................................................3

Task 1
Question A
Bit Error Probability
Bit error probability refers to a unit less execution measure, which is generally
communicated as, “Rate”. The bit blunder likelihood f(x) is the desire estimation of the bit
mistake proportion. The Bit error probability can be considered as its inferred measurement.
F(w)= 1
√ 2 e−√2∨w∨¿ ¿
The Laplacian problem formula can be followed as,
L(f)= 1
√ 2 e−√2∨w∨¿ ¿The -σ 2 w can be considered as the given equation,
f= eat
L(f)= 1
√ 2 e−√2∨w∨¿ ¿
√ 2|w| =∫
0
∞
e− √2 |w| eat dw=∫
0
∞
1
1+e−2¿w∨¿2
dw ¿
= 1
a−w [e ( a−w ) t ]t=∞t=0
Probability of error
= p (w≥ √ p)
=∫
√ w
∞
Fn ( n )dn
=∫
√ p
∞
1
√ 2 e−√ 2 w dw
= ∫
−√ w
∞
1
2 e−t dt
-√2||w||=¿t
pe=w (n>√ w)
1

= ∫
−√ p
∞
1
2 e−tdt
Pe=w(et)
F(w)= ∫
−√ p
∞
1
2 e−tdt
10log10 SNR=10dB
log10 10SNR=1
SNR= 101=10
Pe=W(√SNR)=w(√ 10)
Pe==7.84X10−4
Probability of bit error is,
F(w)= 1
√ 2 e−√2∨w∨¿ ¿
F(√ SNR)= 1
√ 2 e−√2 SNR
BER= 1
√ 2 e−√2.10
= 1
√ 2 e−14.14
Symbol error probability Ps
L(w)= 1
√ 2 e−√2∨w∨¿ ¿
=∫
0
∞
1
√ 2 e−√ 2∨w∨¿ ¿ dw
= 1
√ 2 ∫
0
∞
1
1+e−2∨w∨¿2 ¿ dw
1
√ 2 tan−1 ( x)∫
0
∞
1
1+ e−2∨w∨¿2 ¿ dw
1
√ 2 tan−1 (x)∫
0
∞
e−8 dw = 1
4 =0.25
2

Question B
Here, the ML decoding rule is constructed after detecting the coded signals in (2),
Fn(x)= 1
√ 2 δn
Xexp¿
We consider the given values where,
X axis value is = F(r, s=l) for the limit it can be considered as –l to 0.
Y axis value is = F( r
s =-l) for the limit it can be considered as 0 to ∞ .
Pe= ∫
−1
0
F ( r
s =−l ) dt+ ¿∫
0
∞
F ( r
s =−l ) dt ¿
l=s+w can consider the values of s=1
l=1+w
l+w=1
= { 1l+w
−1−l+w }
s=-l r=-l+ w  w=e+1
3

=F( r
s =-l)= 1
2 l− √ 2|l+1|
Pe= ∫
−1
0
1
√ 2 e− √2 |l +1| dt+∫
1
∞
1
√2 e− √2|l +1| dt
Question C
A specific codeword is selected.
The components of the letter set W=(a, b, c, d), are consistently circulated and will be
decoded with the accompanying code:
C(a)=10011, C(b)=01001,C(c)=00110,C(d)=10101
It is possible to consider the variance values.
The Noise variance as x= δn
δn=1
δ n2=1
N=0
dB= 0:10dB
⋋=l0.⋀ ( dB
lo
)
Pe = 1 and n=1
Ps=¿ ¿ ⋋=snR= Eb
No = Eb
δ n2 = 1
1=l
The errors of the probability can be computed in advanced transmission, the quantity
of bit error is the quantity of the received bits of the information stream over a
correspondence channel that have been modified, because of commotion, obstruction,
bending or bit synchronization errors. The bit error probability pe is the desired estimation of
the bit error proportion.
4

Pe=p(l< i
s )=P(l>0|-s)=Eb( −s
Eb )= 1
√ 2 π e
−w2
4 =l
The decoding of the specific values of the codeword can be considered as the decision on the
transmitted values. The coded components will be transmitted through a discrete channel.
Therefore, the accompanying error can occur on the code with the probability 0.1, 1 rather
than 0 is transmitted and with the probability 0.05, 0 rather than 1 is transmitted. The
received bit-sets will be decoded by C−1. It is required to ascertain the maximal likelihood of
mistake and the normal likelihood of blunder for the code. The issue is that for figuring them,
the probability for the single codeword (λi) is required. Transmitting the codeword contain an
equivalent hamming separations which can pursue the stage, which incorporates the
following,
 Create 4 irregular paired digits.
 Encode them by computing the nth check digits, or utilizing the generator framework
G.
 The codeword through BSC (p) is required.
 Interpret the received 7-bit vector to a 4-bit word.
 Contrast the decoded word and the transmitted word, then check the word errors to
discover the Word Error Rate (WER). Likewise, include the errors that the data places
from the codewords to get the measurement of the decoded Bit Error Rate (BER).
5