Business Statistics Analysis and Interpretation

The provided assignment is focused on the analysis and interpretation of business statistics. The first part involves a profit analysis that compares the impact of shipping type, customer type, and region on product price, sale price, number of customers, and profit. The second part includes an independent two-sample t-test to examine if there are significant differences in average rating between different groups. Correlation analysis is also conducted to determine if there are relationships between product price and profit, sale price and number of customers, and other variables. Furthermore, regression analysis is used to predict monthly profit based on monthly sales. The assignment includes Python code for importing data files and performing statistical tests.

Data Analytics: A Business Case Study
Executive Summary
In Today’s world, eCommerce becoming very popular in all over the world. As the
people got interest in the buying through eCommerce platform, it increases the challenges to
the service provider. It mainly consist of customer satisfaction and increased competition. For
the service provider, it is mandatory to satisfy the customer and compete in the market.
In this case study, we develop the data sets regarding to computer and computer
accessories for the 1000 products. We considered the attributes as Product, Price, Shipping
Type (Free or Customer Paid), Sale Price, Customer Type (New or Existing), Number of
customers, Region (NSW, QLD, VIC, ACT, SA), Profit and Average Rating. We have
calculate some other variables.
We summarised the profit percentage on total sale and profit per item for shipping
type, customer type and region. We test the difference between considered variables for
shipping type, customer type and region. We did correlation and regression analysis.
Analytical findings are reported with conclusion. Recommendations to the company with
implementation plan is also given.
Page 1 of 28

Table of Contents
Sr. No. Topic Page No.
1 List of Abbreviations and assumptions made 3
2 Introduction – What is the problem? 4
3 Research Methodology 6
4 Analytical Findings 6
5 Recommendations to the company 24
6
An implementation plan based on the recommendations you
have provided
24
7 Conclusion 25
8 List of References 26
9 Appendix 27
Page 2 of 28

List of Abbreviations and assumptions made
NSW : New South Wales
QLD : Queensland
VIC : Victoria
ACT : Australian Capital Territory
SA : South Australia
Min : Minimum
Max : Maximum
Q1 : First Quartile
Q3 : Second Quartile
Page 3 of 28

Introduction – What is the problem?
In Today’s world, eCommerce becoming very popular in all over the world. In
Australia, eCommerce market generates about US $ 11789 Million revenue in 2018 and
expected to rise in near future.
eCommerce provides the online platform to the end user to buy the products directly.
This service is very useful for the people who are very busy in their work. eCommerce also
provides offers to the customers which attract the more people. In eCommerce platform,
consumers have more choice in quality, brand, color, price etc.
As the people got interest in the buying through eCommerce platform, it increases the
challenges to the service provider. It mainly consist of customer satisfaction and increased
competition. For the service provider, it is mandatory to satisfy the customer and compete in
the market.
About Data:
In this case study, we develop the data sets regarding to computer and computer
accessories for the 1000 products. We considered the following attributes
i) Product
ii) Price
iii) Shipping Type (Free or Customer Paid)
iv) Sale Price
v) Customer Type (New or Existing)
vi) Number of customers
vii) Region (NSW, QLD, VIC, ACT, SA)
viii) Profit
ix) Average Rating
Page 4 of 28

x) Total monthly sale amount
xi) Total monthly profit
xii) Profit Percentage
We define following variables as
Total Monthly sale amount= Sale Price × Number of customers
Total monthly profit= Profit × Number of customers
Profit Percentage= Total monthly profit /
Project Problem:
We are interested to know the following things
i) Profit analysis by shipping type, customer type and region wise.
ii) Whether there is any association between shipping type and region.
iii) Whether there is any association between customer type and region.
iv) Whether there is any association between shipping type and customer type.
v) Whether the price is significantly different for different shipping type.
vi) Whether the sale price is significantly different for different shipping type.
vii) Whether the profit is significantly different for different shipping type.
viii) Whether the rating is significantly different for different shipping type.
ix) Whether the price is significantly different for different customer type.
x) Whether the sale price is significantly different for different customer type.
xi) Whether the profit is significantly different for different customer type.
xii) Whether the rating is significantly different for different customer type.
xiii) Whether the price is significantly different for different region.
xiv) Whether the sale price is significantly different for different region.
xv) Whether the profit is significantly different for different region.
Page 5 of 28

xvi) Whether the rating is significantly different for different region.
xvii) Correlation analysis of variables
xviii) Regression analysis for total monthly sales
Research Methodology
Statistical tools and techniques are the necessary for analysis. In the analysis,
selection of proper statistical tools and techniques is very important. For profit analysis, we
summarised the profit percentage on total sale and profit per item for shipping type, customer
type and region. We have used the Chi-square test of association for testing the associations
of attributes. We have used independent two sample t-test for the testing the mean price, sale
price, profit and rating for shipping type and customer type. We analyzed the mean price, sale
price, profit and rating of region using one way ANOVA technique. We test the significance
of correlation between two variable. We tried to fit regression model for the monthly profit
and monthly sales.
Analytical Findings
Profit Analysis:
In profit analysis, we have given the total sales amount, total profit, profit percentage
on total sale amount and profit per item. Larger the value of profit percentage on total sale
amount and profit per item would be considered better for increasing the profit.
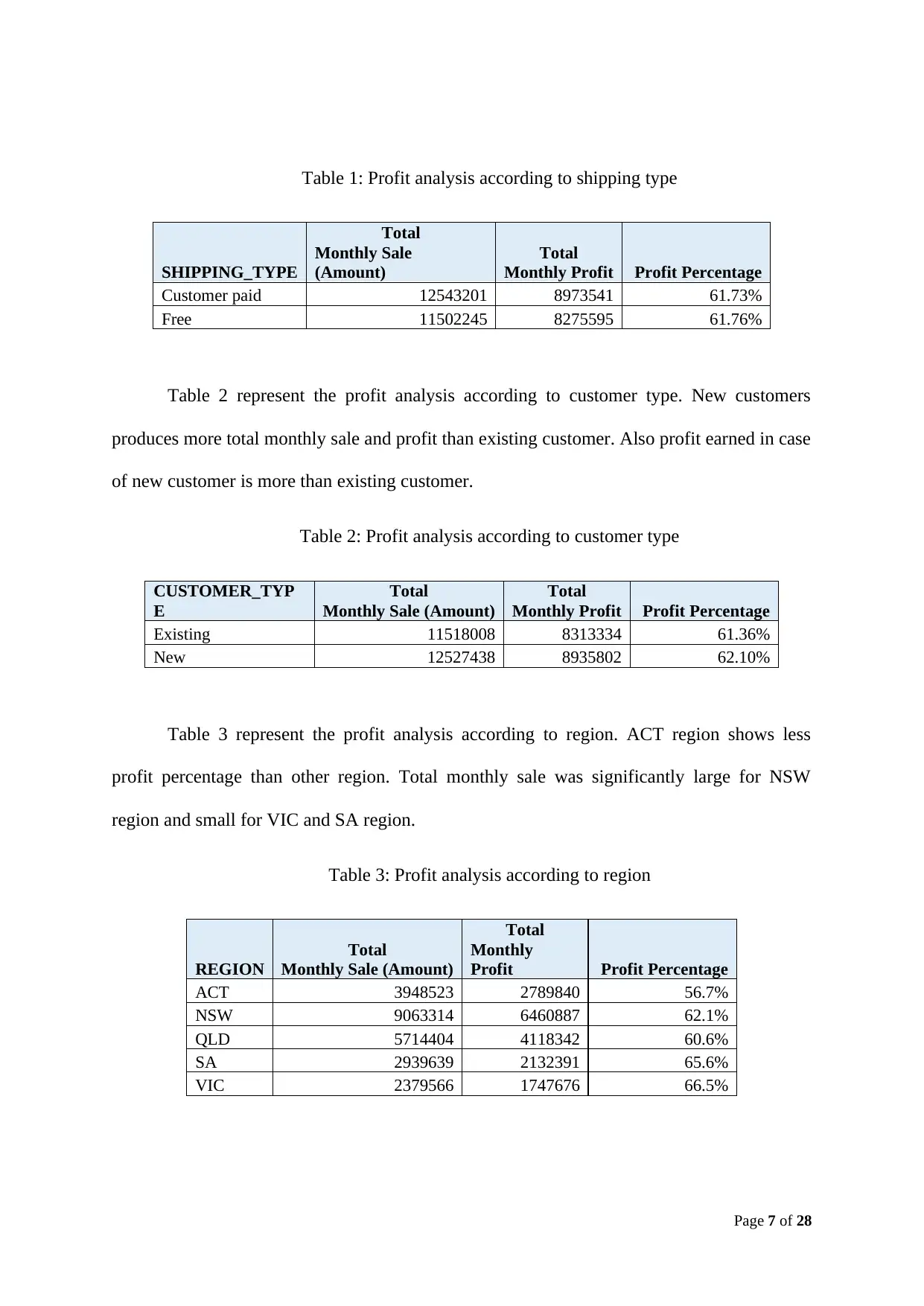
Table 1 gives the profit analysis according to shipping type. Both the shipping type customer
paid and free have no much difference in the average profit percentage. Still total monthly
sale and profit seems to be large for paid shipping customer than free shipping customer.
Page 6 of 28

Table 1: Profit analysis according to shipping type
SHIPPING_TYPE
Total
Monthly Sale
(Amount)
Total
Monthly Profit Profit Percentage
Customer paid 12543201 8973541 61.73%
Free 11502245 8275595 61.76%
Table 2 represent the profit analysis according to customer type. New customers
produces more total monthly sale and profit than existing customer. Also profit earned in case
of new customer is more than existing customer.
Table 2: Profit analysis according to customer type
CUSTOMER_TYP
E
Total
Monthly Sale (Amount)
Total
Monthly Profit Profit Percentage
Existing 11518008 8313334 61.36%
New 12527438 8935802 62.10%
Table 3 represent the profit analysis according to region. ACT region shows less
profit percentage than other region. Total monthly sale was significantly large for NSW
region and small for VIC and SA region.
Table 3: Profit analysis according to region
REGION
Total
Monthly Sale (Amount)
Total
Monthly
Profit Profit Percentage
ACT 3948523 2789840 56.7%
NSW 9063314 6460887 62.1%
QLD 5714404 4118342 60.6%
SA 2939639 2132391 65.6%
VIC 2379566 1747676 66.5%
Page 7 of 28

Descriptive statistics for profit and rating variable:
From Table 4, we have observed the summary statistics for profit and rating variable.
One can study the properties of variables by observing the summary statistics. For example,
as skewness are negative for both the variables suggest that they are negatively skewed.
Table 4: Descriptive statistics for profit and rating variable
PROFIT Rating
Mean 969.775 2.83622
Standard Error
17.6212
8 0.047632
Median 1023.5 2.72
Mode 1333 5
Standard Deviation
557.233
8 1.506243
Sample Variance
310509.
5 2.268768
Kurtosis -0.50686 -1.00682
Skewness -0.40549 -0.22308
Range 2686 5
Minimum -531 0
Maximum 2155 5
Sum 969775 2836.22
Count 1000 1000
Association between attributes:
Here we test the
H0: There is no association between two attributes.
Vs
H1: There is association between two attributes.
We studied the association between two variables by Chi-square test for association.
We have three pair of attributes for possible association
i) shipping type and region.
Page 8 of 28

ii) customer type and region.
iii) shipping type and customer type.
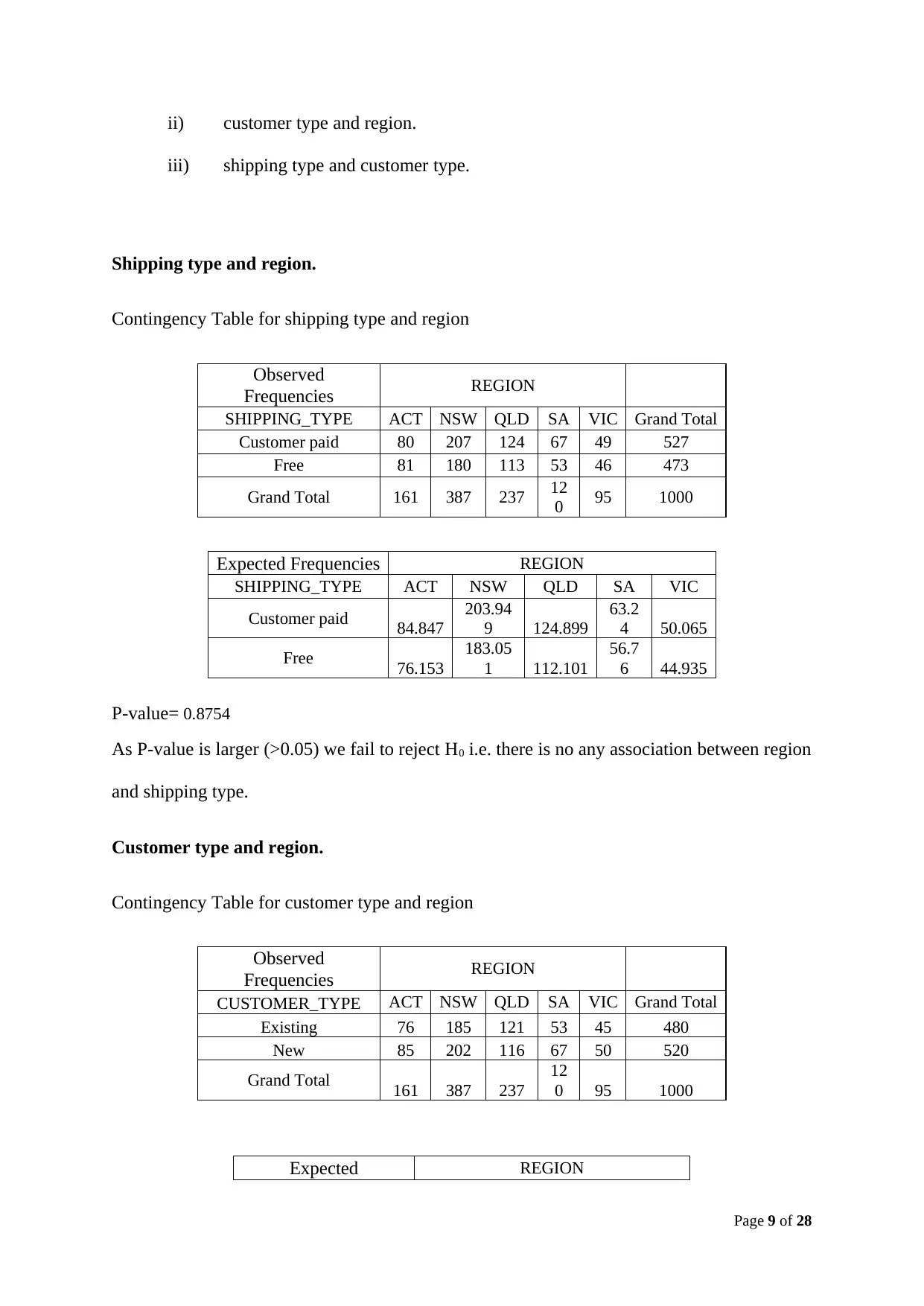
Shipping type and region.
Contingency Table for shipping type and region
Observed
Frequencies REGION
SHIPPING_TYPE ACT NSW QLD SA VIC Grand Total
Customer paid 80 207 124 67 49 527
Free 81 180 113 53 46 473
Grand Total 161 387 237 12
0 95 1000
Expected Frequencies REGION
SHIPPING_TYPE ACT NSW QLD SA VIC
Customer paid 84.847
203.94
9 124.899
63.2
4 50.065
Free 76.153
183.05
1 112.101
56.7
6 44.935
P-value= 0.8754
As P-value is larger (>0.05) we fail to reject H0 i.e. there is no any association between region
and shipping type.
Customer type and region.
Contingency Table for customer type and region
Observed
Frequencies REGION
CUSTOMER_TYPE ACT NSW QLD SA VIC Grand Total
Existing 76 185 121 53 45 480
New 85 202 116 67 50 520
Grand Total 161 387 237
12
0 95 1000
Expected REGION
Page 9 of 28

Frequencies
CUSTOMER_TYPE ACT NSW QLD SA VIC
Existing 77.28 185.76
113.7
6 57.6 45.6
New 83.72 201.24
123.2
4 62.4 49.4
P-value= 0.7990
As P-value is larger (>0.05) we fail to reject H0 i.e. there is no any association between region
and customer type.
Customer type and Shipping type.
Contingency Table for customer type and shipping type
Observed
Frequencies SHIPPING_TYPE
CUSTOMER_TYPE Customer paid Free Grand Total
Existing 247 233 480
New 280 240 520
Grand Total 527 473 1000
Expected
Frequencies SHIPPING_TYPE
CUSTOMER_TYPE Customer paid Free
Existing 252.96 227.04
New 274.04 245.96
P-value= 0.4499
As P-value is larger (>0.05) we fail to reject H0 i.e. there is no any association between
customer type and shipping type.
Two Sample t-test:
We test whether there is significant difference between two groups. Here our null and
alternative hypothesis are as follows
H0: There is no significant difference between the two groups (two independent samples).
Vs
Page 10 of 28

H1: There is significant difference between the two groups (two independent samples)
Shipping Type:
In shipping type, we have two groups customer paid and free shipping. We run the Two
Sample t-test for testing the difference of mean of two groups customer paid and free
shipping.
i) Product Price
ii) Sale Price
iii) Number of customers
iv) Profit
v) Rating
Table 5a shows the result of two sample t-test by assuming unequal variances for testing
the difference of mean of two groups customer paid and free shipping of product price. From
Table 5a, we compare the P value=0.409583 > 0.05, so we fail to reject null hypothesis i.e.
there is no significant difference between the mean price of products for which customer paid
shipping charges and free shipping.
Table 5a: t-Test: Two-Sample Assuming Unequal Variances for testing the difference of
mean of two groups customer paid and free shipping of product price
Customer
paid Free
Mean 387.1404 377.7104
Variance 36877.6 28703.86
Observations 527 473
Hypothesized Mean Difference 0
df 998
t Stat 0.824976
P(T<=t) one-tail 0.204791
t Critical one-tail 1.646382
P(T<=t) two-tail 0.409583
t Critical two-tail 1.962344
Page 11 of 28

Table 5b displays the result of two sample t-test by assuming unequal variances for
testing the difference of mean of two groups customer paid and free shipping of sale price.
From Table 5b, we can see that the P value=0.856732 > 0.05, so we fail to reject null
hypothesis i.e. there is no significant difference between the mean sale price of products for
which customer paid shipping charges and free shipping.
Table 5b: t-Test: t-Test: Two-Sample Assuming Unequal Variances for testing the difference
of mean of two groups customer paid and free shipping of sale price
Customer
paid Free
Mean 1355.313 1349.271
Variance 286744.9 272226.6
Observations 527 473
Hypothesized Mean
Difference 0
df 991
t Stat 0.180583
P(T<=t) one-tail 0.428366
t Critical one-tail 1.646393
P(T<=t) two-tail 0.856732
t Critical two-tail 1.962361
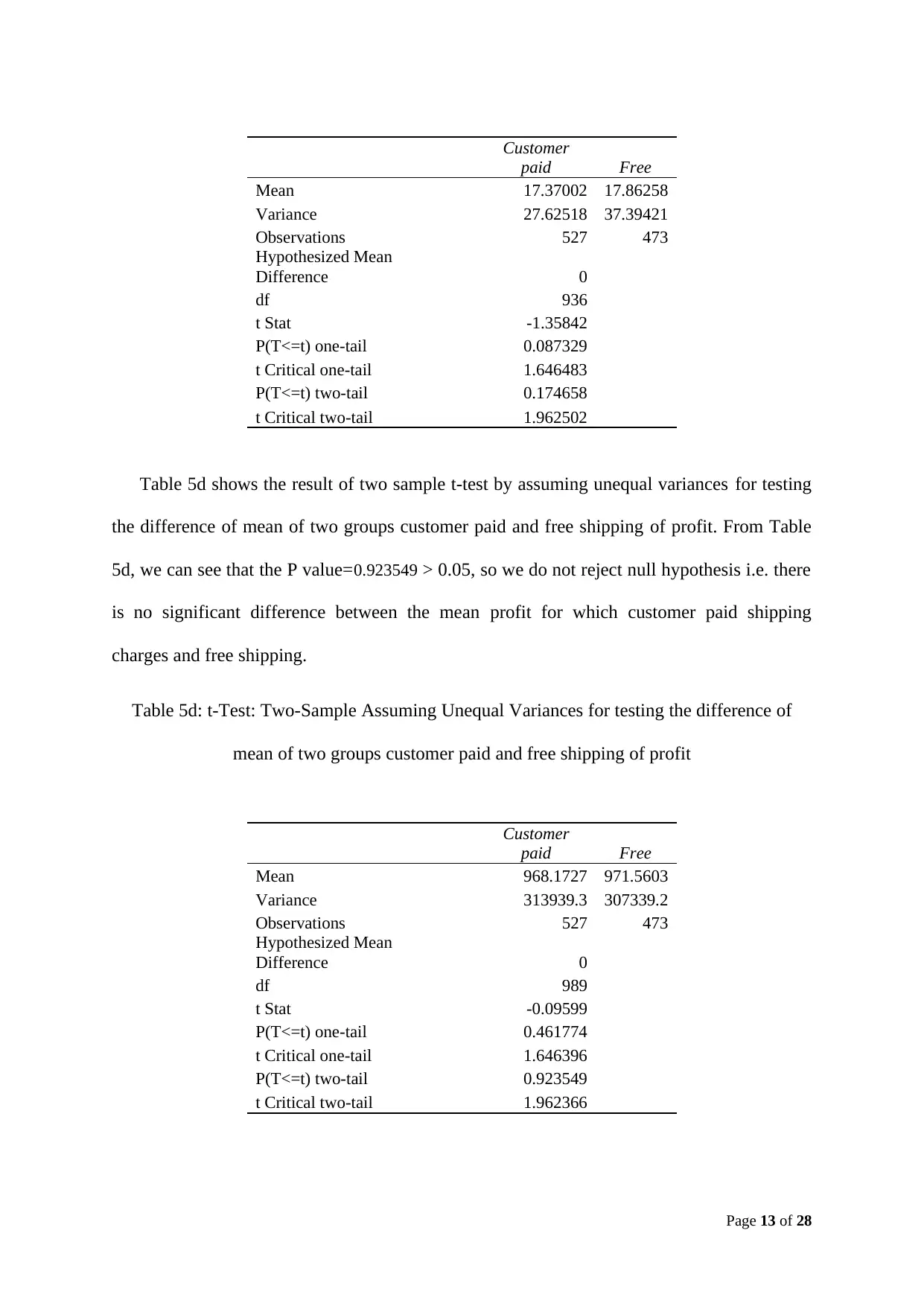
Table 5c demonstrate the result of two sample t-test by assuming unequal variances for
testing the difference of mean of two groups customer paid and free shipping of number of
customers. From Table 5c, we can see that the P value=0.174658 > 0.05, so we fail to reject
null hypothesis i.e. there is no significant difference between the mean number of customers
for which customer paid shipping charges and free shipping.
Table 5c: t-Test: Two-Sample Assuming Unequal Variances for testing the difference of
mean of two groups customer paid and free shipping of number of customers
Page 12 of 28

Customer
paid Free
Mean 17.37002 17.86258
Variance 27.62518 37.39421
Observations 527 473
Hypothesized Mean
Difference 0
df 936
t Stat -1.35842
P(T<=t) one-tail 0.087329
t Critical one-tail 1.646483
P(T<=t) two-tail 0.174658
t Critical two-tail 1.962502
Table 5d shows the result of two sample t-test by assuming unequal variances for testing
the difference of mean of two groups customer paid and free shipping of profit. From Table
5d, we can see that the P value=0.923549 > 0.05, so we do not reject null hypothesis i.e. there
is no significant difference between the mean profit for which customer paid shipping
charges and free shipping.
Table 5d: t-Test: Two-Sample Assuming Unequal Variances for testing the difference of
mean of two groups customer paid and free shipping of profit
Customer
paid Free
Mean 968.1727 971.5603
Variance 313939.3 307339.2
Observations 527 473
Hypothesized Mean
Difference 0
df 989
t Stat -0.09599
P(T<=t) one-tail 0.461774
t Critical one-tail 1.646396
P(T<=t) two-tail 0.923549
t Critical two-tail 1.962366
Page 13 of 28

Table 5e presents the result of two sample t-test by assuming unequal variances for
testing the difference of mean of two groups customer paid and free shipping of rating. From
Table 5e, we can see that the P value < 0.05, so we reject the null hypothesis i.e. there is
significant difference between the mean rating for which customer paid shipping charges and
free shipping.
Table 5e: t-Test: Two-Sample Assuming Unequal Variances for testing the difference of
mean of two groups customer paid and free shipping of rating
Customer
paid Free
Mean 1.996262 3.772072
Variance 1.858913 1.064905
Observations 527 473
Hypothesized Mean
Difference 0
df 971
t Stat -23.3604
P(T<=t) one-tail 1.97E-96
t Critical one-tail 1.646424
P(T<=t) two-tail 3.95E-96
t Critical two-tail 1.96241
Customer Type:
In customer type, we have two groups’ new customer and existing customer. We run the Two
Sample t-test for testing difference between the new customer’s and existing customer’s
mean of
i) Product Price
Page 14 of 28

ii) Sale Price
iii) Number of customers
iv) Profit
v) Rating
Table 6a shows the result of two sample t-test by assuming unequal variances for mean of
product price. From Table 6a, we compare the P value=0.75979 > 0.05, so we fail to reject
null hypothesis i.e. there is no significant difference between the mean price of products for
the new customer and existing customer.
Table 6a: t-Test: Two-Sample Assuming Unequal Variances for testing the difference of
mean of new customer’s and exiting customer’s product price
Existing
Customer
New
Customer
Mean 380.8521 384.3673
Variance 32279.71 33724.35
Observations 480 520
Hypothesized Mean
Difference 0
df 995
t Stat -0.30584
P(T<=t) one-tail 0.379895
t Critical one-tail 1.646386
P(T<=t) two-tail 0.75979
t Critical two-tail 1.962351
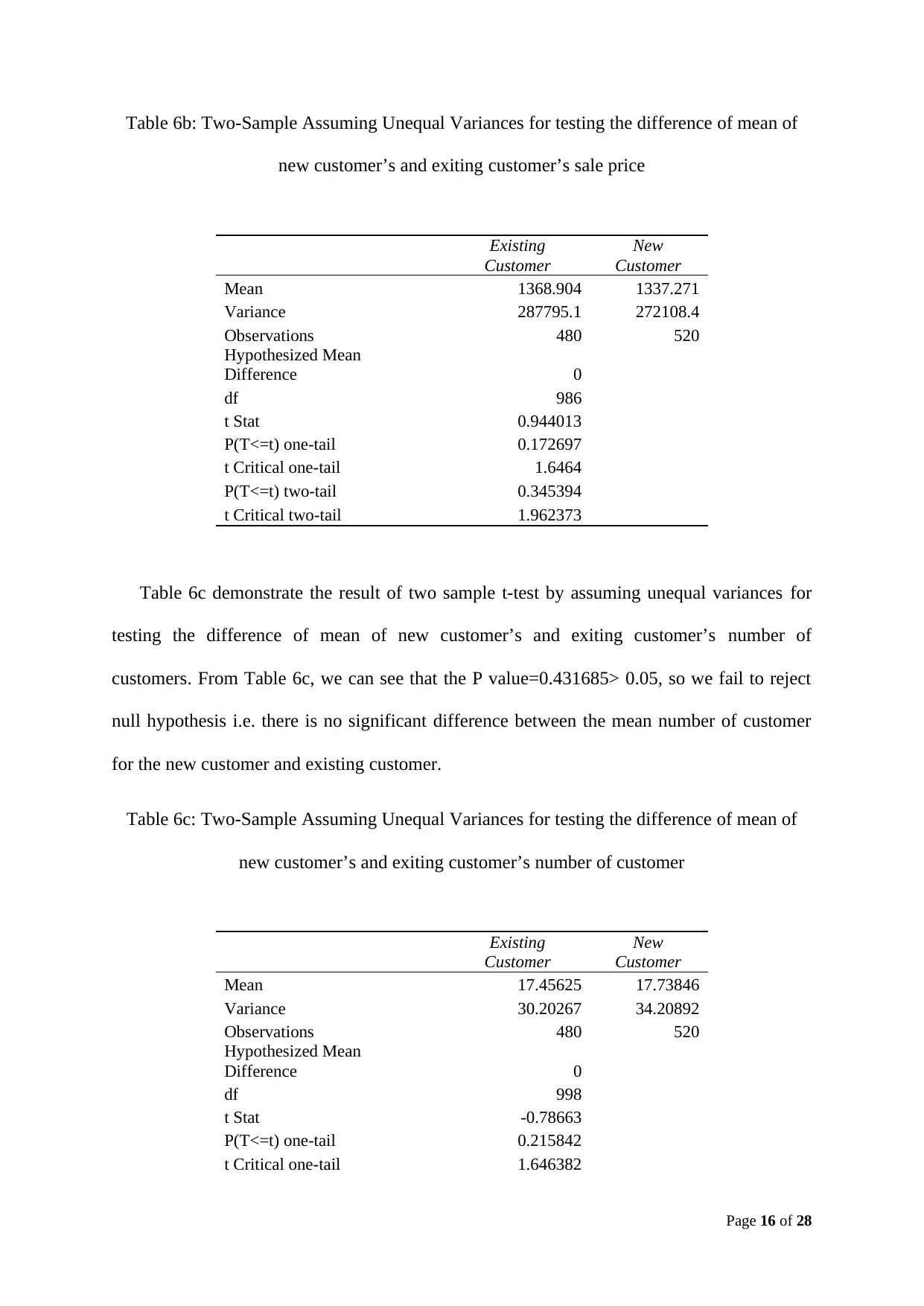
Table 6b displays the result of two sample t-test by assuming unequal variances for
testing the difference of mean of new customer’s and exiting customer’s product price. From
Table 6b, we can see that the P value=0.345394> 0.05, so we fail to reject null hypothesis i.e.
there is no significant difference between the mean sale price of products for the new
customer and existing customer.
Page 15 of 28

Table 6b: Two-Sample Assuming Unequal Variances for testing the difference of mean of
new customer’s and exiting customer’s sale price
Existing
Customer
New
Customer
Mean 1368.904 1337.271
Variance 287795.1 272108.4
Observations 480 520
Hypothesized Mean
Difference 0
df 986
t Stat 0.944013
P(T<=t) one-tail 0.172697
t Critical one-tail 1.6464
P(T<=t) two-tail 0.345394
t Critical two-tail 1.962373
Table 6c demonstrate the result of two sample t-test by assuming unequal variances for
testing the difference of mean of new customer’s and exiting customer’s number of
customers. From Table 6c, we can see that the P value=0.431685> 0.05, so we fail to reject
null hypothesis i.e. there is no significant difference between the mean number of customer
for the new customer and existing customer.
Table 6c: Two-Sample Assuming Unequal Variances for testing the difference of mean of
new customer’s and exiting customer’s number of customer
Existing
Customer
New
Customer
Mean 17.45625 17.73846
Variance 30.20267 34.20892
Observations 480 520
Hypothesized Mean
Difference 0
df 998
t Stat -0.78663
P(T<=t) one-tail 0.215842
t Critical one-tail 1.646382
Page 16 of 28

P(T<=t) two-tail 0.431685
t Critical two-tail 1.962344
Table 6d presents the result of two sample t-test by assuming unequal variances for
testing the difference of mean of new customer’s and exiting customer’s profit. From Table
6d, we can see that the P value=0.319876> 0.05, so we fail to reject null hypothesis i.e. there
is no significant difference between the mean profit for the new customer and existing
customer.
Table 6d: Two-Sample Assuming Unequal Variances for testing the difference of mean of
new customer’s and exiting customer’s profit
Existing
Customer
New
Customer
Mean 988.0521 952.9038
Variance 321110 300730.3
Observations 480 520
Hypothesized Mean
Difference 0
df 985
t Stat 0.995215
P(T<=t) one-tail 0.159938
t Critical one-tail 1.646402
P(T<=t) two-tail 0.319876
t Critical two-tail 1.962375
Table 6e presents the result of two sample t-test by assuming unequal variances for
testing the difference of mean of new customer’s and exiting customer’s rating. From Table
Page 17 of 28

6e, we can see that the P value < 0.05, so we reject null hypothesis i.e. there is significant
difference between the mean rating for the new customer and existing customer.
Table 6e: Two-Sample Assuming Unequal Variances for testing the difference of mean of
new customer’s and exiting customer’s rating
Existing
Customer
New
Customer
Mean 1.875688 3.722865
Variance 1.770462 1.092094
Observations 480 520
Hypothesized Mean Difference 0
df 908
t Stat -24.2784
P(T<=t) one-tail 4.8E-101
t Critical one-tail 1.646534
P(T<=t) two-tail 9.7E-101
t Critical two-tail 1.96258
One way ANOVA:
In this section, we test whether the mean of different region is not significantly different. We
run the one way ANOVA for testing whether the different region have different mean or not
for
i) Product Price
ii) Sale Price
iii) Number of customers
iv) Profit
v) Rating
Table 7 represent the descriptive statistics for the Product Price, Sale Price, Number of
customers, Profit and Rating for different region.
Page 18 of 28

Table 7: Summary statistics for the Product Price, Sale Price, Number of customers, Profit
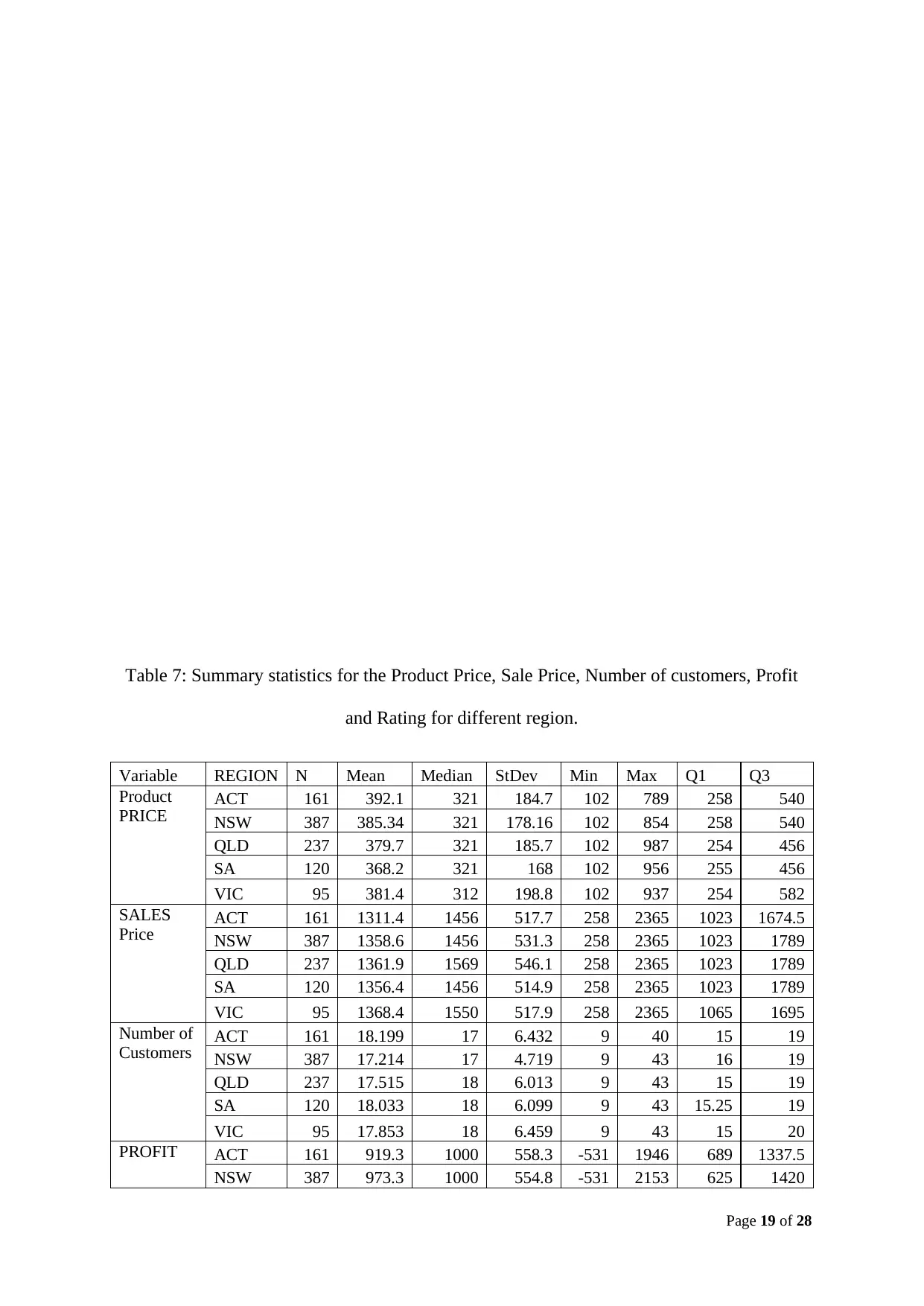
and Rating for different region.
Variable REGION N Mean Median StDev Min Max Q1 Q3
Product
PRICE ACT 161 392.1 321 184.7 102 789 258 540
NSW 387 385.34 321 178.16 102 854 258 540
QLD 237 379.7 321 185.7 102 987 254 456
SA 120 368.2 321 168 102 956 255 456
VIC 95 381.4 312 198.8 102 937 254 582
SALES
Price ACT 161 1311.4 1456 517.7 258 2365 1023 1674.5
NSW 387 1358.6 1456 531.3 258 2365 1023 1789
QLD 237 1361.9 1569 546.1 258 2365 1023 1789
SA 120 1356.4 1456 514.9 258 2365 1023 1789
VIC 95 1368.4 1550 517.9 258 2365 1065 1695
Number of
Customers ACT 161 18.199 17 6.432 9 40 15 19
NSW 387 17.214 17 4.719 9 43 16 19
QLD 237 17.515 18 6.013 9 43 15 19
SA 120 18.033 18 6.099 9 43 15.25 19
VIC 95 17.853 18 6.459 9 43 15 20
PROFIT ACT 161 919.3 1000 558.3 -531 1946 689 1337.5
NSW 387 973.3 1000 554.8 -531 2153 625 1420
Page 19 of 28

QLD 237 982.1 1154 589.9 -420 2145 617 1408
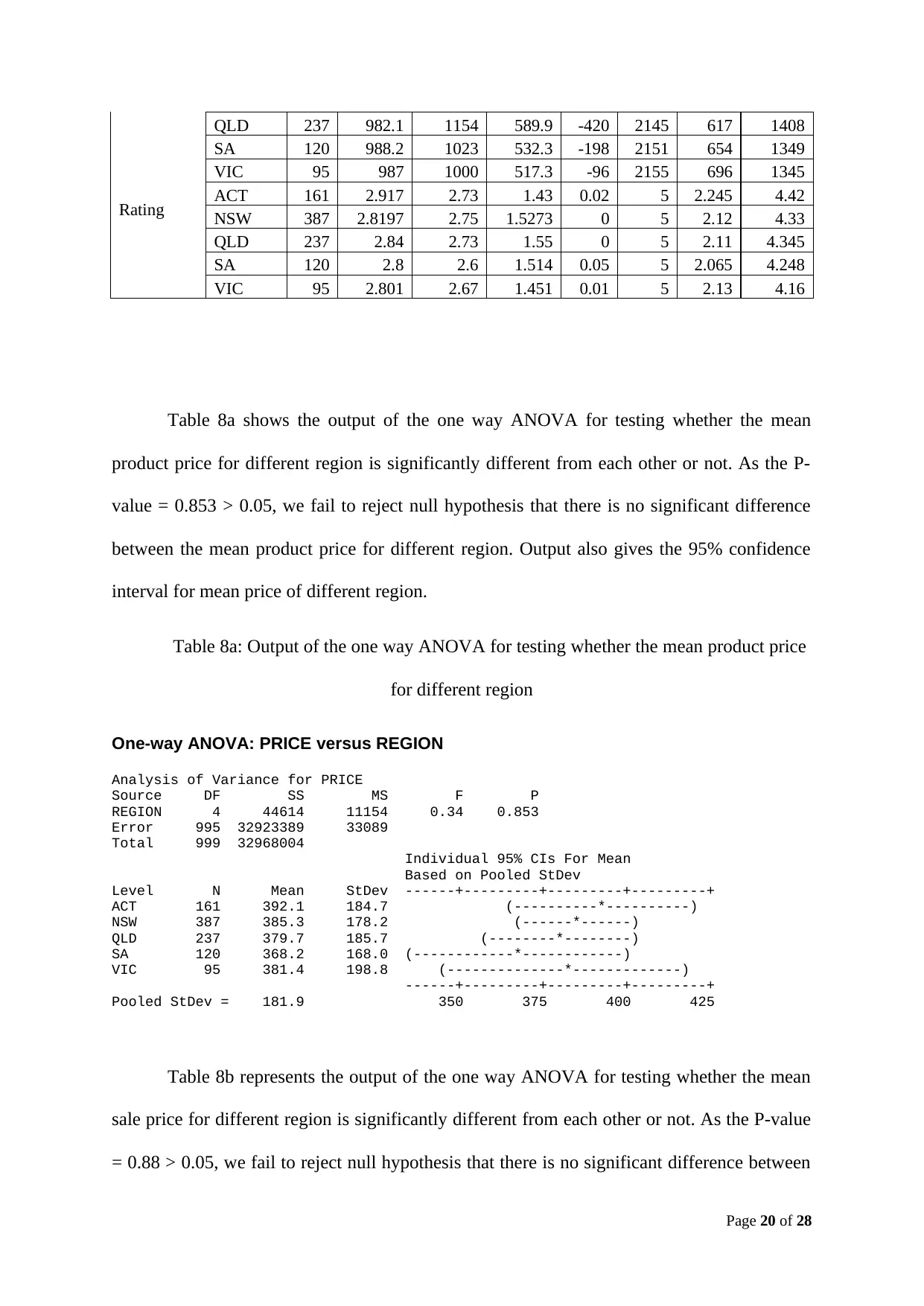
SA 120 988.2 1023 532.3 -198 2151 654 1349
VIC 95 987 1000 517.3 -96 2155 696 1345
Rating ACT 161 2.917 2.73 1.43 0.02 5 2.245 4.42
NSW 387 2.8197 2.75 1.5273 0 5 2.12 4.33
QLD 237 2.84 2.73 1.55 0 5 2.11 4.345
SA 120 2.8 2.6 1.514 0.05 5 2.065 4.248
VIC 95 2.801 2.67 1.451 0.01 5 2.13 4.16
Table 8a shows the output of the one way ANOVA for testing whether the mean
product price for different region is significantly different from each other or not. As the P-
value = 0.853 > 0.05, we fail to reject null hypothesis that there is no significant difference
between the mean product price for different region. Output also gives the 95% confidence
interval for mean price of different region.
Table 8a: Output of the one way ANOVA for testing whether the mean product price
for different region
One-way ANOVA: PRICE versus REGION
Analysis of Variance for PRICE
Source DF SS MS F P
REGION 4 44614 11154 0.34 0.853
Error 995 32923389 33089
Total 999 32968004
Individual 95% CIs For Mean
Based on Pooled StDev
Level N Mean StDev ------+---------+---------+---------+
ACT 161 392.1 184.7 (----------*----------)
NSW 387 385.3 178.2 (------*------)
QLD 237 379.7 185.7 (--------*--------)
SA 120 368.2 168.0 (------------*------------)
VIC 95 381.4 198.8 (--------------*-------------)
------+---------+---------+---------+
Pooled StDev = 181.9 350 375 400 425
Table 8b represents the output of the one way ANOVA for testing whether the mean
sale price for different region is significantly different from each other or not. As the P-value
= 0.88 > 0.05, we fail to reject null hypothesis that there is no significant difference between
Page 20 of 28

the mean sale price for different region. Output also gives the 95% confidence interval for
mean sale price of different region.
Table 8b: Output of the one way ANOVA for testing whether the mean sale price for
different region
One-way ANOVA: SALES versus REGION
Analysis of Variance for SALES
Source DF SS MS F P
REGION 4 333084 83271 0.30 0.880
Error 995 278994796 280397
Total 999 279327880
Individual 95% CIs For Mean
Based on Pooled StDev
Level N Mean StDev -----+---------+---------+---------+-
ACT 161 1311.4 517.7 (----------*-----------)
NSW 387 1358.6 531.3 (------*-------)
QLD 237 1361.9 546.1 (---------*--------)
SA 120 1356.4 514.9 (-------------*------------)
VIC 95 1368.4 517.9 (--------------*---------------)
-----+---------+---------+---------+-
Pooled StDev = 529.5 1260 1330 1400 1470
Table 8c demonstrates the output of the one way ANOVA for testing whether the
mean number of customers for different region is significantly different from each other or
not. As the P-value = 0.342 > 0.05, we fail to reject null hypothesis that there is no significant
difference between the mean number of customers for different region. We can look at the
95% confidence interval for mean number of customers of different region.
Table 8c: Output of the one way ANOVA for testing whether the mean number of
customers for different region
One-way ANOVA: NO_OF_CUSTOMERS versus REGION
Analysis of Variance for NO_OF_CU
Source DF SS MS F P
REGION 4 145.6 36.4 1.13 0.342
Error 995 32095.8 32.3
Total 999 32241.4
Individual 95% CIs For Mean
Based on Pooled StDev
Level N Mean StDev ---+---------+---------+---------+---
ACT 161 18.199 6.432 (------------*------------)
NSW 387 17.214 4.719 (-------*-------)
QLD 237 17.515 6.013 (---------*----------)
SA 120 18.033 6.099 (--------------*-------------)
Page 21 of 28

VIC 95 17.853 6.459 (---------------*---------------)
---+---------+---------+---------+---
Pooled StDev = 5.680 16.80 17.50 18.20 18.90
Table 8d reveals the output of the one way ANOVA for testing whether the mean
profit for different region is significantly different from each other or not. As the P-value =
0.795 > 0.05, we fail to reject null hypothesis that there is no significant difference between
the mean profit for different region. We can observe the 95% confidence interval for mean
profit of different region.
Table 8d: Output of the one way ANOVA for testing whether the mean profit for
different region
One-way ANOVA: PROFIT versus REGION
Analysis of Variance for PROFIT
Source DF SS MS F P
REGION 4 520860 130215 0.42 0.795
Error 995 309678180 311234
Total 999 310199040
Individual 95% CIs For Mean
Based on Pooled StDev
Level N Mean StDev ------+---------+---------+---------+
ACT 161 919.3 558.3 (----------*----------)
NSW 387 973.3 554.8 (------*------)
QLD 237 982.1 589.9 (--------*--------)
SA 120 988.2 532.3 (------------*-----------)
VIC 95 987.0 517.3 (-------------*-------------)
------+---------+---------+---------+
Pooled StDev = 557.9 880 960 1040 1120
Table 8e shows the output of the one way ANOVA for testing whether the mean
rating for different region is significantly different from each other or not. As the P-value =
0.959 > 0.05, we fail to reject null hypothesis that there is no significant difference between
Page 22 of 28

the mean rating for different region. We can observe the 95% confidence interval for mean
rating of different region.
Table 8e: Output of the one way ANOVA for testing whether the mean rating for
different region
One-way ANOVA: Average Rating versus REGION
Analysis of Variance for Average Rating
Source DF SS MS F P
REGION 4 1.44 0.36 0.16 0.959
Error 995 2265.06 2.28
Total 999 2266.50
Individual 95% CIs For Mean
Based on Pooled StDev
Level N Mean StDev ------+---------+---------+---------+
ACT 161 2.917 1.430 (-----------*-----------)
NSW 387 2.820 1.527 (-------*-------)
QLD 237 2.840 1.550 (---------*---------)
SA 120 2.800 1.514 (------------*-------------)
VIC 95 2.801 1.451 (--------------*--------------)
------+---------+---------+---------+
Pooled StDev = 1.509 2.60 2.80 3.00 3.20
Correlation Analysis:
In the following Table 9, we represent the Pearson’s correlation coefficient and P-value of its
significance for Product Price, Sale Price, Number of customers, Profit and Rating.
Table 9: Pearson’s correlation coefficient and P-value of its significance for Product Price,
Sale Price, Number of customers, Profit and Rating
Product Price Sale Price Number of customers Profit
Sale Price 0.011
0.73
Number of
customers 0.058 0.079
0.066 0.012
Profit -0.316 0.945 0.056
0 0 0.075
Rating 0.158 -0.31 0.016 -0.346
0 0 0.618 0
From Table 9, we can say that following pair has significant correlation
Page 23 of 28

i) Product price and Profit
ii) Product price and Rating
iii) Sale price and Number of customers
iv) Sale price and Profit
v) Sale price and Rating
vi) Profit and Rating
Regression analysis:
We considered the monthly profit as a response variable and monthly sale as a
predictor variable. Table 10 displays the output of simple liner regression on monthly profit
by monthly sales. We observed that R2 =89% which pretty high suggest that model fitting is
good. We can predict the monthly profit by observing the monthly sales using regression
equation.
Table 10: Regression analysis of monthly profit by monthly sales
Regression Analysis: Monthly_Profit versus Monthly_Sale
The regression equation is
Monthly_Profit = - 3625 + 0.868 Monthly_Sale
Predictor Coef SE Coef T P
Constant -3624.6 263.6 -13.75 0.000
Monthly_ 0.868094 0.009670 89.77 0.000
S = 3928 R-Sq = 89.0% R-Sq(adj) = 89.0%
Analysis of Variance
Source DF SS MS F P
Regression 1 1.24337E+11 1.24337E+11 8058.92 0.000
Residual Error 998 15397640608 15428498
Total 999 1.39735E+11
Recommendations to the company
i) From profit analysis, there is very low monthly sales for VIC and SA region compare to
the others. So company has to pay attention for more marketability for this region.
Page 24 of 28

ii) Average rating of customers who got delivery free is higher than those who got the
delivery by paying so company need to plan to provide the items
iii) Average rating of new customers is higher than existing customer suggest that we need
to plan to satisfies our existing customers to avoid the shifting to any other company for
service.
An implementation plan based on the recommendations you have provided
i) As the VIC and SA region have less monthly sale it gives you less profit, so company
should focus on attract the customers for purchasing the costly gadget. Company can
appoint the marketing executive for marketing the costly gadgets. (As number of
customers are not significantly different for the regions)
ii) Company can increase the staff of shipping department so that more customer gets free
delivery which highly impact on rating.
iii) Company must give some offer to the existing customers such as price cut, free
shipping etc. so that it impact on the rating.
Conclusions
From the profit analysis, we can say that shipping type and customer type does not
show any significant changes in the profit whereas different region have different have
different profit. From two sample t-test for shipping type and customer type, average rating
shows significant difference between the groups whereas other variables as product price,
sale price, number of customers and profit does not show any significance difference between
the groups. There is no any significant difference between the different region for product
price, sale price, number of customers, profit and rating. Correlation analysis suggest that
there is significant correlation between Product price and Profit, Product price and Rating,
Sale price and Number of customers, Sale price and Profit, Sale price and Rating, Profit and
Rating. Regression analysis shows that we can predict the monthly profit by observing the
monthly sales. They are positively correlates.
Page 25 of 28

Page 26 of 28

List of References
i) Berenson, M., Levine, D., Szabat, K.A. and Krehbiel, T.C., 2012. Basic business
statistics: Concepts and applications. Pearson higher education AU.
ii) Bickel, P.J. and Doksum, K.A., 2015. Mathematical statistics: basic ideas and
selected topics, volume I (Vol. 117). CRC Press.
iii) Black, K., 2009. Business statistics: Contemporary decision making. John Wiley &
Sons.
iv) Bowerman, B.L., O'Connell, R.T., Murphree, E., Huchendorf, S.C. and Porter, D.C.,
2003. Business statistics in practice(pp. 728-730). New York: McGraw-Hill/Irwin.
v) Casella, G. and Berger, R.L., 2002. Statistical inference (Vol. 2). Pacific Grove, CA:
Duxbury.
vi) DeGroot, M.H. and Schervish, M.J., 2012. Probability and statistics. Pearson
Education.
vii) Groebner, D.F., Shannon, P.W., Fry, P.C. and Smith, K.D., 2008. Business statistics.
Pearson Education.
viii) Hodges Jr, J.L. and Lehmann, E.L., 2005. Basic concepts of probability and statistics.
Society for Industrial and Applied Mathematics.
ix) Kvanli, A.H., Pavur, R.J. and Guynes, C.S., 2000. Introduction to business statistics.
Cincinnati, OH: South-Western.
x) Mendenhall, W. and Sincich, T., 1993. A second course in business statistics:
Regression analysis. San Francisco: Dellen.
xi) Papoulis, A., 1990. Probability & statistics (Vol. 2). Englewood Cliffs: Prentice-Hall.
xii) Pillers Dobler, Carolyn. "Mathematical statistics: Basic ideas and selected topics."
(2002): 332-332.
xiii) Ross, S.M., 2014. Introduction to probability and statistics for engineers and
scientists. Academic Press.
Page 27 of 28