Microeconomics Assignment: Consumer Choice and Cost Functions Analysis
VerifiedAdded on 2023/04/22
|5
|681
|309
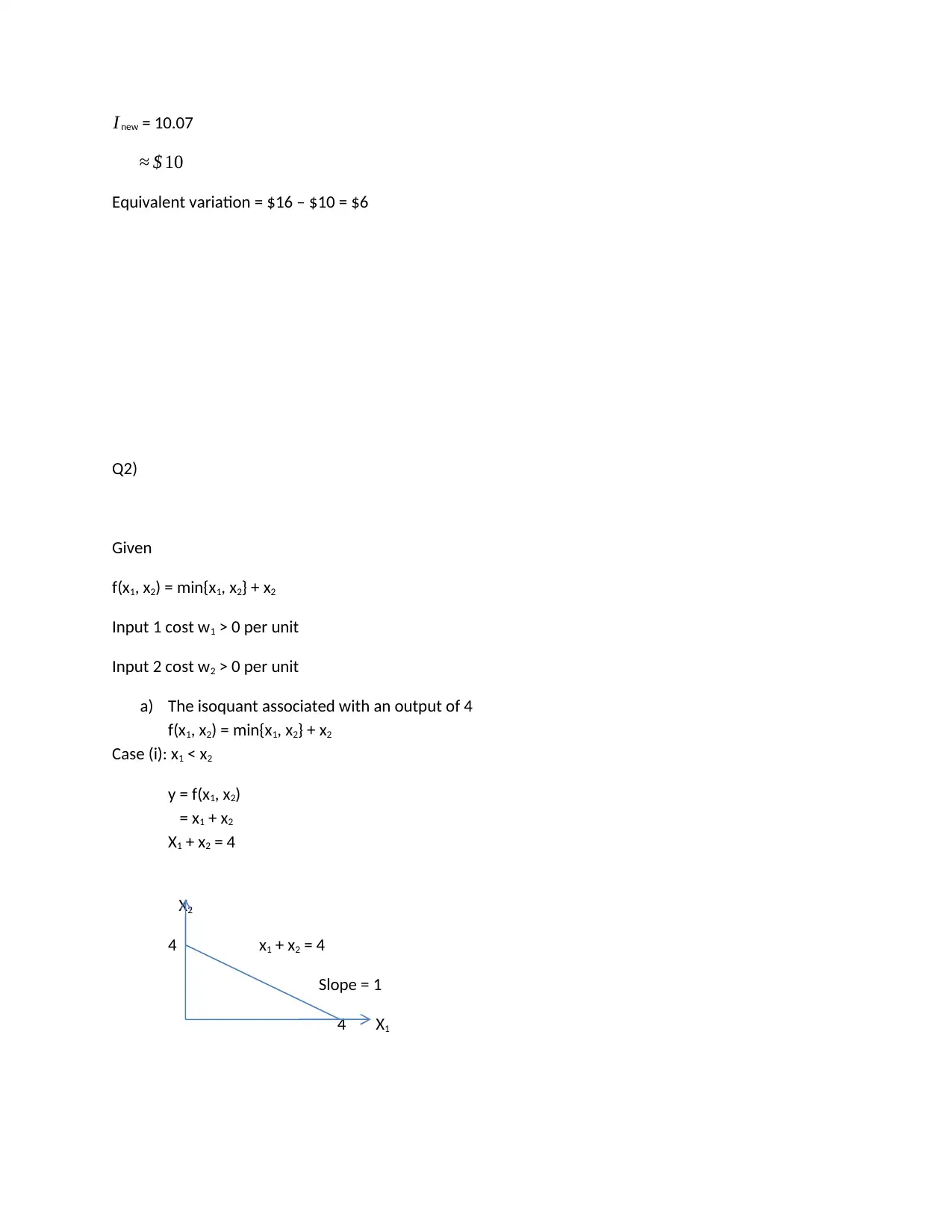
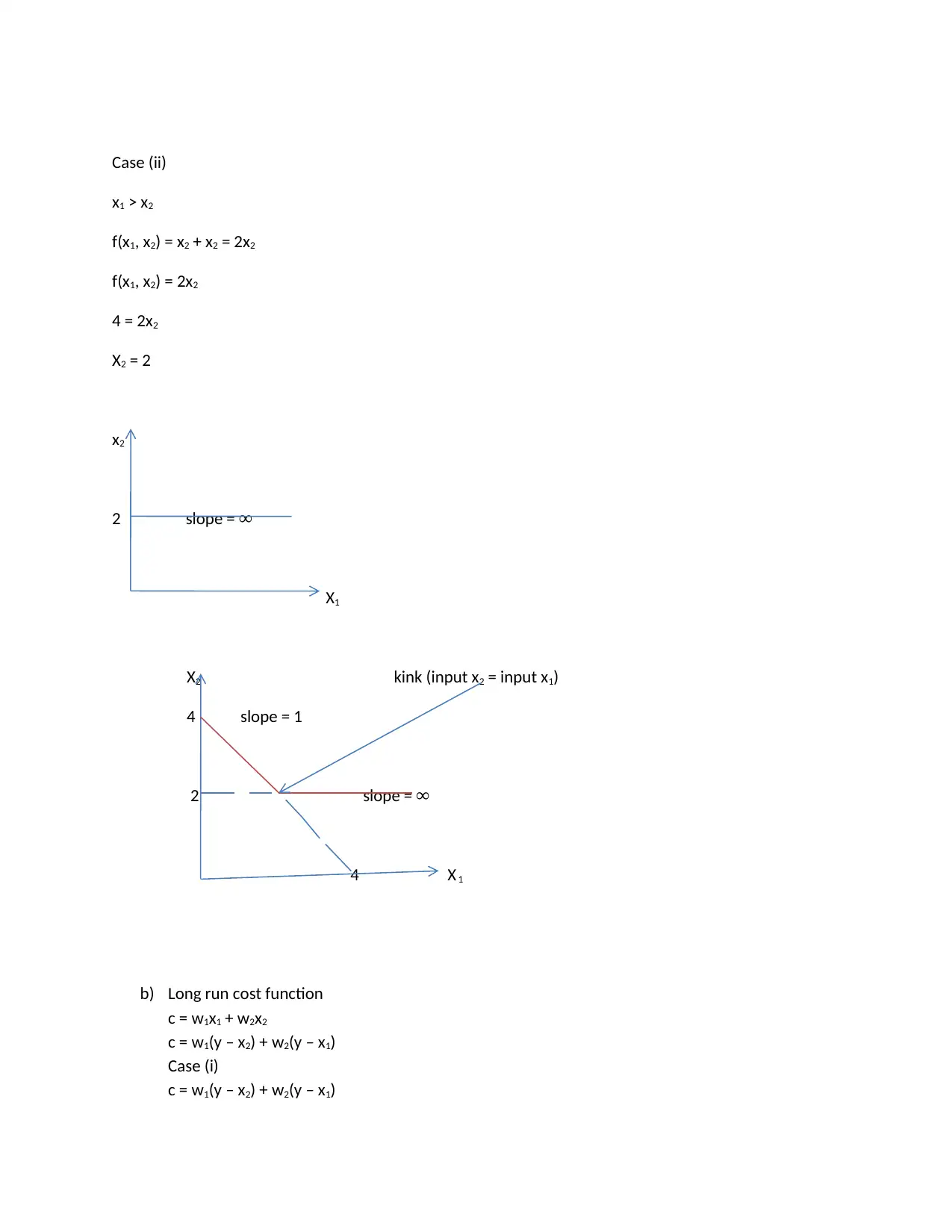
Homework Assignment
AI Summary
This economics homework assignment addresses core microeconomic concepts including utility functions, consumer choice, and cost analysis. The first question explores utility maximization, calculating compensating and equivalent variations in response to price changes, considering a specific utility function and income levels. The solution details the calculations for both scenarios. The second question delves into cost functions, analyzing a production function with two inputs, and deriving the associated isoquants and long-run cost function. The solution provides a breakdown of the isoquant's shape and derives the long-run cost function based on different input relationships. The assignment provides a comprehensive analysis of consumer behavior and production costs, offering insights into how economic agents make decisions under various constraints.
1 out of 5










![[object Object]](/_next/static/media/star-bottom.7253800d.svg)