A-Star Algorithm: Pathfinding Algorithm for Finding Shortest Path

The A* algorithm is one of most used pathfinding algorithm which mainly finds the shortest path between multiple points also known as nodes. In this algorithm a combination of two heuristic functions are applied to search for next iteration.

A-Star Algorithm:
The A* algorithm is one of most used pathfinding algorithm which mainly finds the shortest
path between multiple points also known as nodes. In this algorithm a combination of two
heuristic functions are applied to search for next iteration. One heuristic function is h(n)
which mainly finds the estimate of the how the vertex n is away from the target node T. The
h(n) is also admissible that is it never overestimates the distance from current node to goal.
Another heuristic function in A* is g(n) which is the distance measured from current node to
the strating node. Now, in this particular case the nodes are all the grids in the square size
which is developed in MATLAB. The source is the robot starting position and the destination
is the End poisition in the grid which is chosen by user. Furthermore, the user can also choose
as many blockades as desired in step by step manner in unit grid points. The A star algorithm
finds the best (minimum distance) route from starting position to End position of the robot.
The route is shown by simulation in MATLAB.
Algorithm methodology:
The brief of the algorithm is the following. All the positions of obstacles, start and end are
extracted as given by the user. The starting position is also added in obstacle array as the
robot will not move in starting position. In map start, end, obstacles and empty grid points are
labelled as 1,0,-1 and 2. Then the initial heuristics h(0) and g(0) are calculated and then the
total cost f(0) = h(0) + g(0) is obtained. h(0) is calculated by a distance function defined in
distance.m. Then the queue in first step is calculated by the insert.m function where starting
positions, ending position as parent nodes and their respective costs h(n), g(n) and f(n) are
taken as inputs and stored in the queue function. Now, the Astar main alogrithm is applied
inside a while loop where the exploration and queues after each explloration is updated by

expand_node.m and queue_fn.m. The loop continues till there exist a path between start and
the ending node and current node is not equals to the target node. Finally, the costs in each
iteration, queues in each step and the shortest path followed bhy the robot is displayed by the
result.m function. The shortest path is also shown by the line plot in the grid.
The expnasion of the A* algorithm is less expensive in comparison to dijkstra algorithm and
given by the follwing cost function relation.
f(n) = g(n) + h(n)
Here, f(n) = total distance through cuurent node
g(n) = so far cost to reach the node n
h(n) = estimated cost from current node to goal node.
Calculation of h(n) can be computed either by the Manhattan distance or by Euclidean
distance heuristics. Manhattan distance is calculated by summing the total number of squares
moved horizontally and vertically to reach the destination node from the starting node.
h=|xstart – xend|+|ystart − yend|
This is less accurate than the Eucildean distance heuristic but for computation Manhattan
distance is faster than Eucildean distance as in Euclidean distance a large area is needed to be
explored for finding the path. In this algorithm the Euclidean distance heuristics is employed
to find the cost due to its accuracy feature. The euclidean distance is given by,
h = √ ( xstart −xend ) 2 + ( ystart − yend ) 2
Flowchart of A* algorithm:

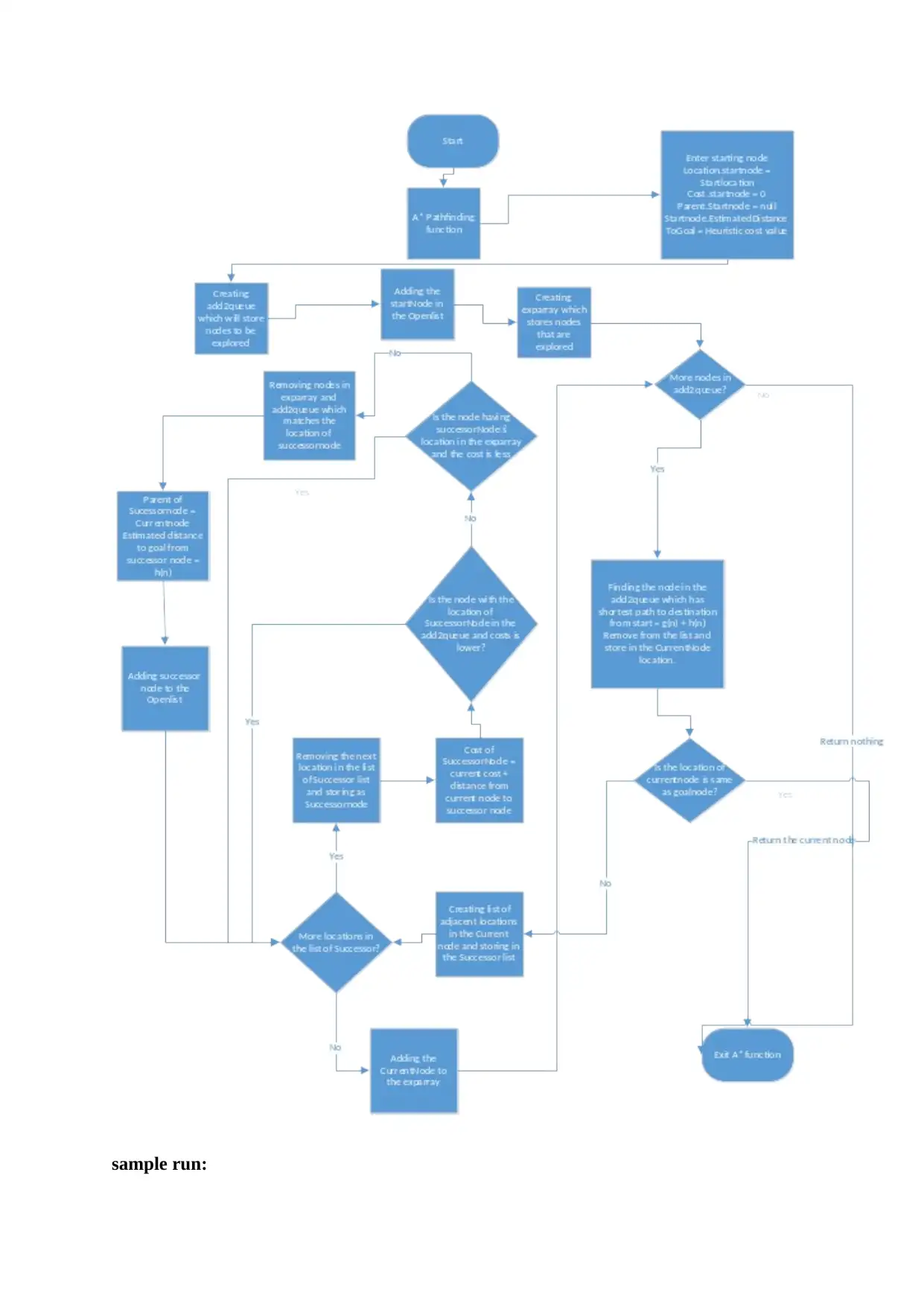
sample run:

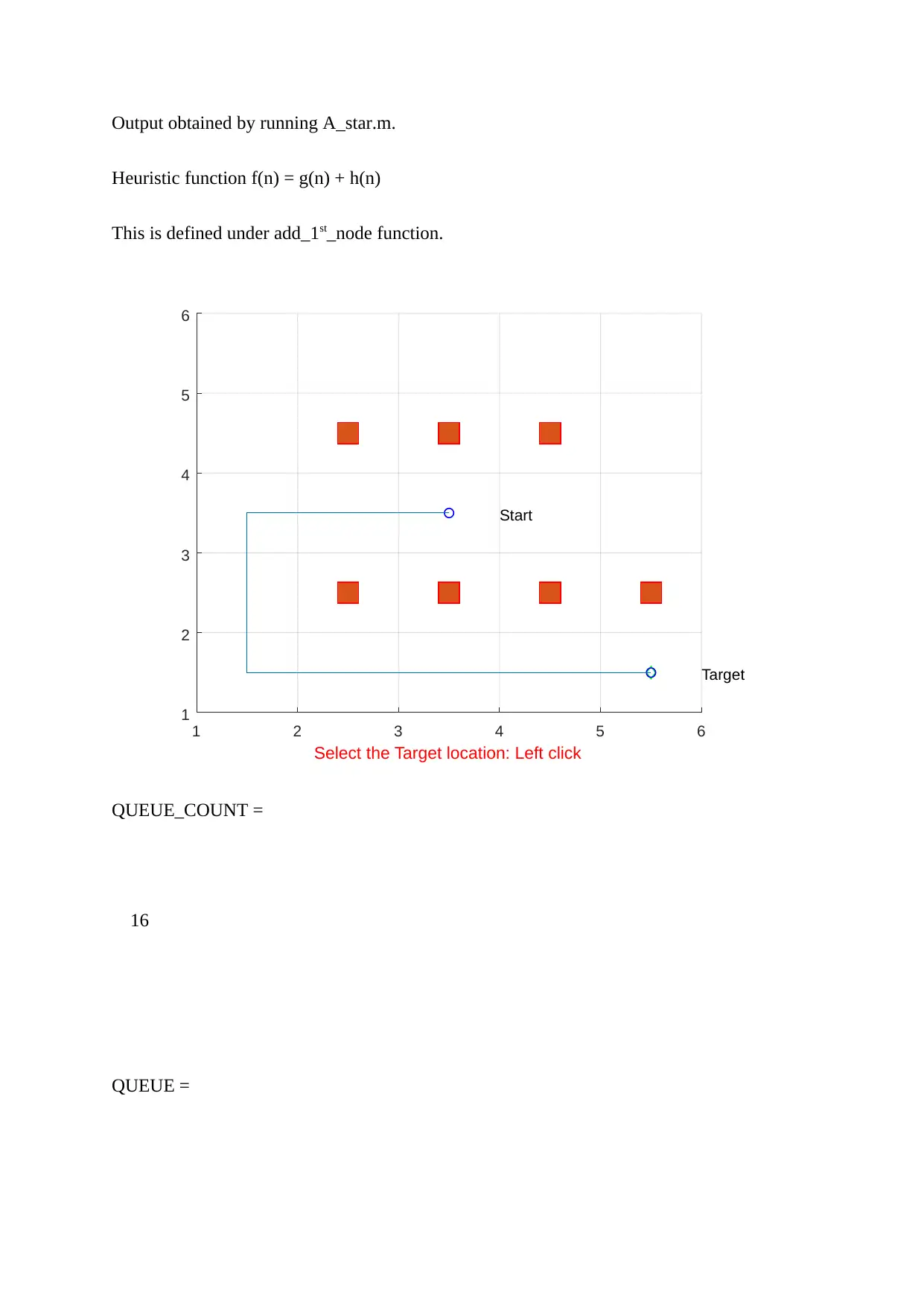
Output obtained by running A_star.m.
Heuristic function f(n) = g(n) + h(n)
This is defined under add_1st_node function.
1 2 3 4 5 6
Select the Target location: Left click
1
2
3
4
5
6
Start
Target
QUEUE_COUNT =
16
QUEUE =

0 3.0000 3.0000 3.0000 3.0000 0 0 0
0 2.0000 3.0000 3.0000 3.0000 1.0000 3.6056 4.6056
0 4.0000 3.0000 3.0000 3.0000 1.0000 2.2361 3.2361
0 5.0000 3.0000 4.0000 3.0000 2.0000 2.0000 4.0000
0 5.0000 4.0000 5.0000 3.0000 3.0000 3.0000 6.0000
0 1.0000 3.0000 2.0000 3.0000 2.0000 4.4721 6.4721
0 5.0000 5.0000 5.0000 4.0000 4.0000 4.0000 8.0000
0 1.0000 2.0000 1.0000 3.0000 3.0000 4.1231 7.1231
0 1.0000 4.0000 1.0000 3.0000 3.0000 5.0000 8.0000
0 1.0000 1.0000 1.0000 2.0000 4.0000 4.0000 8.0000
1.0000 4.0000 5.0000 5.0000 5.0000 5.0000 4.1231 9.1231
1.0000 1.0000 5.0000 1.0000 4.0000 4.0000 5.6569 9.6569
0 2.0000 1.0000 1.0000 1.0000 5.0000 3.0000 8.0000
0 3.0000 1.0000 2.0000 1.0000 6.0000 2.0000 8.0000
0 4.0000 1.0000 3.0000 1.0000 7.0000 1.0000 8.0000
0 5.0000 1.0000 4.0000 1.0000 8.0000 0 8.0000
Dijkstra’s Algorithm:

Dijkstra’s algorithm is a uniform cost search algorithm where the shortest distance is
calculated based on the heuristic of g(n) which is the shortest distance from the starting node
to the current node. Hence, for employing Dijkstra we don’t need the distance.m function and
always set the h(n) equal to zero. These two modifications are done in expand_node.m and
addfirstnode.m function. The queues of the Dijkstra’s algorithm is large and the queue count
is higher compared to A* algorithm as more unnecessary explorations are performed in each
step. This variation in queue can be observed by setting same start, target and obstacle grid
points on the map.
Dijkstra’s Algorithm sample run:
Output obtained by running Dijkstra.m
Heuristic function f(n) = g(n)
This is changed in Add_1st_node.m function. All the rest codes are same.
Sample Run:

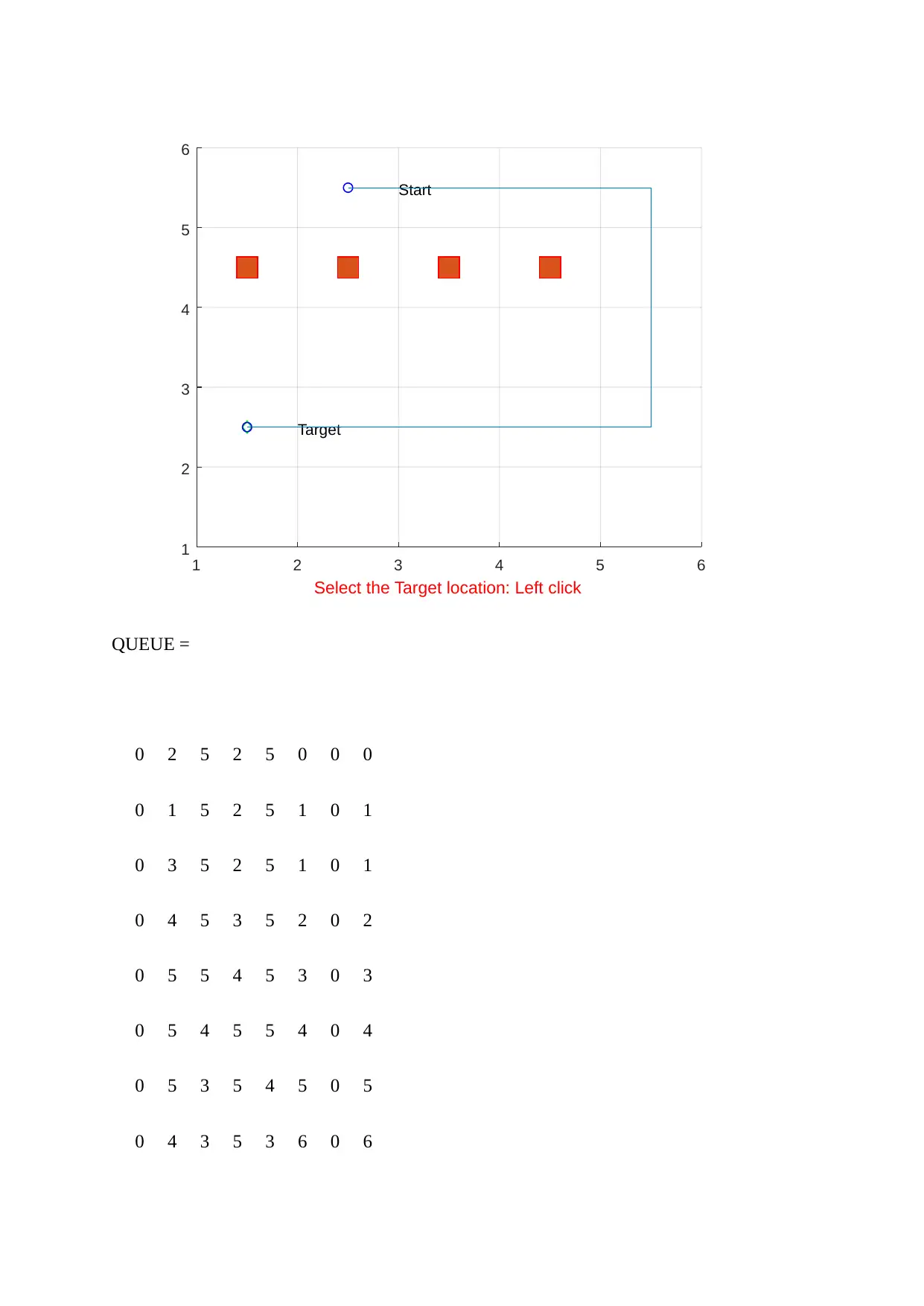
1 2 3 4 5 6
Select the Target location: Left click
1
2
3
4
5
6
Start
Target
QUEUE =
0 2 5 2 5 0 0 0
0 1 5 2 5 1 0 1
0 3 5 2 5 1 0 1
0 4 5 3 5 2 0 2
0 5 5 4 5 3 0 3
0 5 4 5 5 4 0 4
0 5 3 5 4 5 0 5
0 4 3 5 3 6 0 6

0 5 2 5 3 6 0 6
1 3 3 4 3 7 0 7
1 4 2 4 3 7 0 7
QUEUE =
0 2 5 2 5 0 0 0
0 1 5 2 5 1 0 1
0 3 5 2 5 1 0 1
0 4 5 3 5 2 0 2
0 5 5 4 5 3 0 3
0 5 4 5 5 4 0 4
0 5 3 5 4 5 0 5
0 4 3 5 3 6 0 6
0 5 2 5 3 6 0 6
0 3 3 4 3 7 0 7
0 4 2 5 2 7 0 7
1 5 1 5 2 7 0 7
1 2 3 3 3 8 0 8

1 3 2 3 3 8 0 8
QUEUE =
0 2 5 2 5 0 0 0
0 1 5 2 5 1 0 1
0 3 5 2 5 1 0 1
0 4 5 3 5 2 0 2
0 5 5 4 5 3 0 3
0 5 4 5 5 4 0 4
0 5 3 5 4 5 0 5
0 4 3 5 3 6 0 6
0 5 2 5 3 6 0 6
0 3 3 4 3 7 0 7
0 4 2 5 2 7 0 7
0 5 1 5 2 7 0 7
1 2 3 3 3 8 0 8
1 3 2 4 2 8 0 8
1 4 1 4 2 8 0 8

QUEUE =
0 2 5 2 5 0 0 0
0 1 5 2 5 1 0 1
0 3 5 2 5 1 0 1
0 4 5 3 5 2 0 2
0 5 5 4 5 3 0 3
0 5 4 5 5 4 0 4
0 5 3 5 4 5 0 5
0 4 3 5 3 6 0 6
0 5 2 5 3 6 0 6
0 3 3 4 3 7 0 7
0 4 2 5 2 7 0 7
0 5 1 5 2 7 0 7
0 2 3 3 3 8 0 8
0 3 2 4 2 8 0 8
1 4 1 5 1 8 0 8
1 1 3 2 3 9 0 9

1 2 2 2 3 9 0 9
QUEUE =
0 2 5 2 5 0 0 0
0 1 5 2 5 1 0 1
0 3 5 2 5 1 0 1
0 4 5 3 5 2 0 2
0 5 5 4 5 3 0 3
0 5 4 5 5 4 0 4
0 5 3 5 4 5 0 5
0 4 3 5 3 6 0 6
0 5 2 5 3 6 0 6
0 3 3 4 3 7 0 7
0 4 2 5 2 7 0 7
0 5 1 5 2 7 0 7
0 2 3 3 3 8 0 8
0 3 2 4 2 8 0 8
0 4 1 5 1 8 0 8

1 1 3 2 3 9 0 9
1 2 2 3 2 9 0 9
1 3 1 3 2 9 0 9
QUEUE =
0 2 5 2 5 0 0 0
0 1 5 2 5 1 0 1
0 3 5 2 5 1 0 1
0 4 5 3 5 2 0 2
0 5 5 4 5 3 0 3
0 5 4 5 5 4 0 4
0 5 3 5 4 5 0 5
0 4 3 5 3 6 0 6
0 5 2 5 3 6 0 6
0 3 3 4 3 7 0 7
0 4 2 5 2 7 0 7
0 5 1 5 2 7 0 7
0 2 3 3 3 8 0 8

0 3 2 4 2 8 0 8
0 4 1 5 1 8 0 8
0 1 3 2 3 9 0 9
0 2 2 3 2 9 0 9
1 3 1 4 1 9 0 9
1 1 2 1 3 10 0 10
QUEUE =
0 2 5 2 5 0 0 0
0 1 5 2 5 1 0 1
0 3 5 2 5 1 0 1
0 4 5 3 5 2 0 2
0 5 5 4 5 3 0 3
0 5 4 5 5 4 0 4
0 5 3 5 4 5 0 5
0 4 3 5 3 6 0 6
0 5 2 5 3 6 0 6
0 3 3 4 3 7 0 7

0 4 2 5 2 7 0 7
0 5 1 5 2 7 0 7
0 2 3 3 3 8 0 8
0 3 2 4 2 8 0 8
0 4 1 5 1 8 0 8
0 1 3 2 3 9 0 9
0 2 2 3 2 9 0 9
0 3 1 4 1 9 0 9
1 1 2 2 2 10 0 10
1 2 1 2 2 10 0 10
QUEUE_COUNT=
20
g_cost=
10