Classical Hypothesis Testing in Statistics

This document provides an overview of classical hypothesis testing in statistics. It explains the null and alternative hypotheses, the use of Two Sample T-test, the calculation of test statistics, the decision rule, and the assumptions made in the test. The document also includes a summary of the results and references for further reading.

STATISTICS

STATISTICS
Question a
The hypotheses for this classical hypothesis testing approach are as given below;
H0 (Null Hypothesis): The prices for SPDR Gold EFT and Spot Gold do not differ.
H1 (Alternative Hypothesis): The prices for SPDR Gold EFT and Spot Gold differ.
In the development of the hypotheses above, the interest for the study is considered. In
this case, the interest is primarily in observing the prices for SPDR Gold EFT and Spot Gold.
The purpose for this observation is determining whether the prices for SPDR Gold EFT and Spot
Gold are significantly different.
Thus, this information forms the basis for the development of the necessary research
hypotheses with the price being the variable of interest. The null hypothesis is based on there
being no difference between the prices for SPDR Gold EFT and Spot Gold hence; H0 (Null
Hypothesis): The prices for SPDR Gold EFT and Spot Gold do not differ. While the alternative
hypothesis is based on there being a difference between the prices for SPDR Gold EFT and Spot
Gold hence; H1 (Alternative Hypothesis): The prices for SPDR Gold EFT and Spot Gold differ.
Question b
Since interest in this study is to determine whether there is a difference in prices for
SPDR Gold EFT and Spot Gold, then a Two Sample T-test is the appropriate test for this study.
The Two Sample T-test is a statistical test that compares the means of two different populations
to determine whether the two populations significantly differ from each other (O'Neil & Schutt,
2013; Everitt & Skrondal, 2010).
2

STATISTICS
In this study, the two populations are the SPDR Gold EFT and Spot Gold. The Two
Sample T-test therefore compares the mean prices in the samples drawn from these two
populations in order to establish whether the prices for SPDR Gold EFT and Spot Gold
significantly differ from each other.
Step 1
The mathematical representation of the hypotheses is therefore given as below:
H0 : x1 =x2
H1 : x1 ≠ x2
Step 2
The level of significance for this study has been provided for as; α level of significance =
0.01. this value will be used for the testing of the hypothesis stated in step 1 above. This implies
that for this study, the probability of rejecting the null hypothesis when it is true is 0.01.
Step 3
The test statistics for the Two Sample T-test is as given below (Barbara & Susan, 2014);
t= [ x1 −x2 ] −d
SE
Where,
x1=mean of sample ¿ population 1
3

STATISTICS
x2=mean of sample ¿ population 2
d=hypothesized difference∈means
SE=Standard Error
Since our test is two-tailed and the hypothesized difference in means = 0, then the test
statistics is modified as follows:
t= [ x1 −x2 ]
SE
Step 4
The decision rule for the Two Sample T-test is as follows; if the p-value is less than the
level of significance, the null hypothesis is rejected, while if the p-value exceeds the level of
significance we fail to reject the null hypothesis (Norman, 2010).
Step 5
The results from the Two Sample T-test in this study are given in Table 1: Two Sample
T-test Summary Output below:
Table 1: Two Sample T-test Summary Output
t-Test: Two-Sample Assuming Unequal Variances
Variable 1 Variable 2
Mean 124.9548714 127.5928204
4

STATISTICS
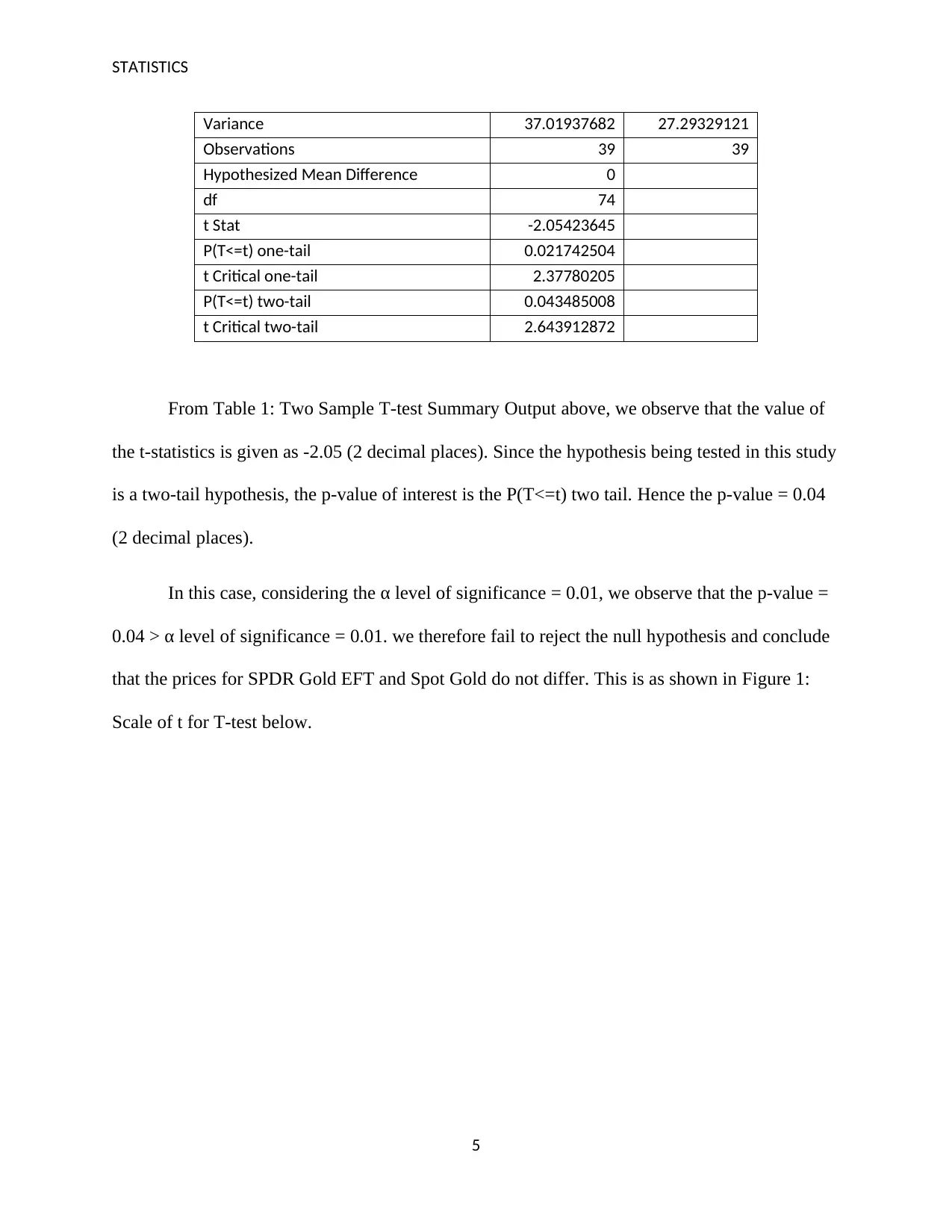
Variance 37.01937682 27.29329121
Observations 39 39
Hypothesized Mean Difference 0
df 74
t Stat -2.05423645
P(T<=t) one-tail 0.021742504
t Critical one-tail 2.37780205
P(T<=t) two-tail 0.043485008
t Critical two-tail 2.643912872
From Table 1: Two Sample T-test Summary Output above, we observe that the value of
the t-statistics is given as -2.05 (2 decimal places). Since the hypothesis being tested in this study
is a two-tail hypothesis, the p-value of interest is the P(T<=t) two tail. Hence the p-value = 0.04
(2 decimal places).
In this case, considering the α level of significance = 0.01, we observe that the p-value =
0.04 > α level of significance = 0.01. we therefore fail to reject the null hypothesis and conclude
that the prices for SPDR Gold EFT and Spot Gold do not differ. This is as shown in Figure 1:
Scale of t for T-test below.
5

STATISTICS
Figure 1: Scale of t for T-test
From the data provided on the historical prices for SPDR Gold EFT and Spot Gold,
statistical analysis show that there does not exist any significant difference in the prices for
SPDR Gold EFT and Spot Gold.
Question c
The following assumptions were made for the Two Sample T-test carried out in this study
(Han & Jaiwei, 2011; Howitt & Cramer, 2010):
1. The two samples are assumed to be independent of each other.
2. The two samples are assumed to be normally distributed or approximately normally
distributed.
It is important that the samples are independent of each other. Here, we assume that the
two populations and hence the samples drawn from them are independent. This reduces chances
the correlation which would otherwise make the results unreliable.
6

STATISTICS
Similarly, the assumption on normality is significant for the same reason. High variance,
which is common in data drawn from non-normal distributions give incorrect results for the test
statistics and hence unreliable.
References
7

STATISTICS
Barbara, I., & Susan, D. (2014). Introductory Statistics (1st ed.). New York: OpenStax CNX.
Everitt, B. S., & Skrondal, A. (2010). Cambridge Dictionary of Statistics (4th ed.). London:
Cambridge University Press.
Han, K., & Jaiwei, P. (2011). Data Mining: Concepts and Techniques (3rd ed.). London: Morgan
Kaufman.
Howitt, D., & Cramer, D. (2010). Introduction to Descriptive Statistics in Psycology, 5th
Edition. New York: Prentice Hall.
Norman, G. (2010). Likert Scales, Levels of Measurement and the Laws of Statistics. Advances
in Health Science Education , 15(5), 625-632.
O'Neil, C., & Schutt, R. (2013). Doing Data Science (3rd ed.). London: O'Reily.
8