Advanced Algorithm Analysis: Recurrence Trees, Divide-and-Conquer Technique, and Universal Sink

This article covers advanced algorithm analysis topics such as recurrence trees, divide-and-conquer technique, and universal sink. It includes explanations, examples, and proofs. The time complexity of algorithms is also discussed. Course code and college/university are not mentioned.

ADVANCED ALGORITHM ANALYSIS
[Author Name(s), First M. Last, Omit Titles and Degrees]
[Institutional Affiliation(s)]

Question 1
Suppose nI=1, then it means nE=2nI+1=2+1=3;
Suppose nI=0, then nE=2nI+1=1
Making a presumption that for k’<k, the equation nE holds, an equation provided in the form nI
=k’<k, the condition nE=2nI+1 is true.
Giving consideration to nI=k, then it follows that nE=2(k-1) + (3-1). This is interpreted as the
total external nodes is equivalent to the external nodes composed of k-1 nodes in addition to
3(the addition of 3 refers to the internal nodes that have 3 children) removing 1 (this is a
replacement of the external node that was changed into an internal node when creating a new
internal node). An inference can thus be reached at that nE=2k-2+3=2k+1
Question 2
The algorithm adopts the divide-and-conquer technique. While adopting this divide-and-conquer
technique, an alternation in the lengths of the two sorted arrays T and S is notice. Len (T) is used
in the denotation of the length of T while the length of S is denoted using len (S) at any provided
time.
Any certain iteration given, ms=lens (S)/2 is used in the denotation of the medium index of S
besides medium of S by S[ms]. On a similar note, mT=len (T)/ 2 is used in the denotation of the
medium index of T alongside as the medium of T is denoted by T[mt]. mt+ms and S[ms] can
then be compared against T[mt] that aids in finding the half part i.e. right or left of the arrays i.e.
S or T that may be eliminated or discarded to leave the smaller sub-problems for recursion.
The algorithm

1st Condition (ms+mt ≥ k)
Condition 1.1 when S[ms] ≥ T [mt ]
Discarding of the right larger half of array S may be performed that would mean removal from
S[ms] from the end and thereafter recursive determination of the k-th smallest element that is in
T alongside the left smaller half of S
Condition 1.2 when T[mt] ¿ S[ms]
Under this condition, a direct and exact symmetry with condition 1.1 with the arrays T and S
exchanged is noticed
Condition 2 (ms+mt<k):
Condition 2.1 S[ms]≥ T [ mt ]
This condition encompasses the discarding of the left smaller half of T array and then finding the
(k-mt)-th of the smallest element in S alongside in the right large half of array S
Condition 2.2 T[mt]>S[ms]
Similar Condition 1.2, Condition 2.2 has exhibits the exact symmetry with condition 1.1, with
the arrays T and S exchanged
Time complexity: At a specific iteration, discarding of half of some array occurs and thereby the
time complexity becomes O (log (len(S)) +log (len (T))) which can be simplified to O (logn) at
size n as the input of the arrays T and S
Question 3

i) This can be achieved in quite simple manner. The sorting of every list takes the form ak2+bk+
c for certain constants a, b and c. in this case, we have n/k of those constants and hence
n
k ( ak2+bk +c ) =ank +bn+ cn
k =⊝ (nk )
ii) Sorting a sublists of length k would each take
T ( a )=¿
{ 0 if a=1
2T ( a
2 )+ ak if a=2p ,if p> 0
There tends to be, to some extent, sense, in generating the merger as the merging of a single sub
list is trivial while the merging of the a sublists would mean to dividing them into two distinct
groups of lists of a/2, merging each of the groups recursively and then joining the results in steps
of ak being that there are two rays, the length each would be a
2 k
T (1) =1 k lg 1=k.0=0
It is assumed that T (a) =ak lg a and hence T (2a)
T(2a)= 2T(a)+2ak=2(T(a)+ak)=2(ak lg a+ak)=2ak(lg a+1)=2ak (lg a+lg 2)=2ak lg (2a). This
serves as a proof and can thus the number if the sublists n/k can be substituted for a
T ( n
k )= nk
k lg n
k =n lg (n/k )
This condition only holds and is exact hence the power of n/k is 2. From this determination it can
be concluded that the general time complexity of the merge is given by ⊝( nlg n)
(Ratheesh et al., 2016)

iii) The greatest values is given by k=lg n, and via substitution,
⊝ (n lg n+n lg n
lg n )=⊝(lgn),
In case k=f (n)> lg n, then ⊝(nf (n)) would give the complexity would be given by which would
serve as the running time than merge sort.
Question 4
i) For the given recurrence T (n) = 3T (n/2) + n, a=3, b=4 and f (n) =n. for this case, nlogb a =nlog3 2
due to the fact that f (n) =Ω=(n¿ ¿ log3 2+ ϵ)¿ where ϵ =0.2. This makes it possible to deploy the
case 3 of the master theorem if proving the regularity condition would be possible for f (n). The
solution is T (n) =⊝(f ( n))=⊝( n)
ii) The upper and lower boundaries do not matter when it comes to solving recurrences making it
possible to come up with the recurrence tree for the recurrence equation T (n) = 3T (n/2) + n. to
enhance the ease of working with numbers that can easily be determined, it is assumed that n is
to an precise power of 2 and this would see all the sizes of the subproblem being integers. The
recurrence tree for T (n) = 3T (n/2) + n is thus as follows:

As can be observed from the recurrence tree, there is a reduction in the sizes of the subproblem
by a constant factor of 2 every step down a level and finally a boundary of T (1) is attained as the
last level of the recurrence tree (Ratheesh et al., 2016). The size of the subproblem for any node
at the second depth i is found to be n/2i when determining the depth of the tree and hence the size
of the subproblem gest to n=1 at the point n/2i or its equivalent at i=lgn. The three therefore
remains to have lgn+1 levels with the depth sequence being 0, 1, 2, 3…, lgn
After completion of calculating the depth of the tree, the immediate step is about the
determination of the cost at each level of the tree of entire four levels. Since each level has at
least thrice more nodes in comparison with the previous level, 3i describes the total number of
nodes at the depth i. The subproblem size for every node had been determined to reduce by a
constant factor of 2 for every of the level as one comes down from the top of the tree; hence each
node whose depth i for i=0, 1, 2, 3…, lgn-1 costs n/2i. The full cost is attained by finding the
product of the cost of each node, n/2i, and the total number of nodes, 3i, 3i* n/2i= (3/2) in. The
depth is at lgn at the lowest level of the tree; at which there are 3lgn=nlog3 nodes and every node of

them contributes a cost T (1) making the overall cost to be nlog3 T (1). This is simplified as
⊝( nlg3 ) as it is assumed that T (1) is a constant in the equation hence cancelling out.
Adding together all the costs at each level generates the cost of the whole recurrence tree and it
calculated using the equation:
T ( n )=n+ 3
2 n+( 3
2 )
2
n+( 3
2 )
3
n+…+ ( 3
2 )lgn−1
n+⊝(nlg 3)
¿ ∑
k=0
lgn−1
(3
2 )
k
n+¿ ⊝(nlg3 )¿
=
( 3
2 )
lgn−1
3
2 −1
n+⊝(nlg3 )
=2 nlg 3−2 n+⊝( nlg3 )=⊝( nlg3 )
iii) Proving the answer
For all the integers n, s.t≥ 1 at the Property P (n)
The presence of a seemingly close match between the form T (n) ≤ dnlg 3−cn for some of the
constants d as well as c where c>0 and d>0 gives an impression of a close resemblance of the
recurrence T (n) = 3T (n/2) + n
Question 5
There is only one vertex that can be a universal sink following its definition. In the definition of ,
the i-th column all need to be ‘1’ while all the i-th row need to be ‘0’ of the adjacency-matrix
excluding the entry of aii. The algorithm is thus described to establish the existence of a universal

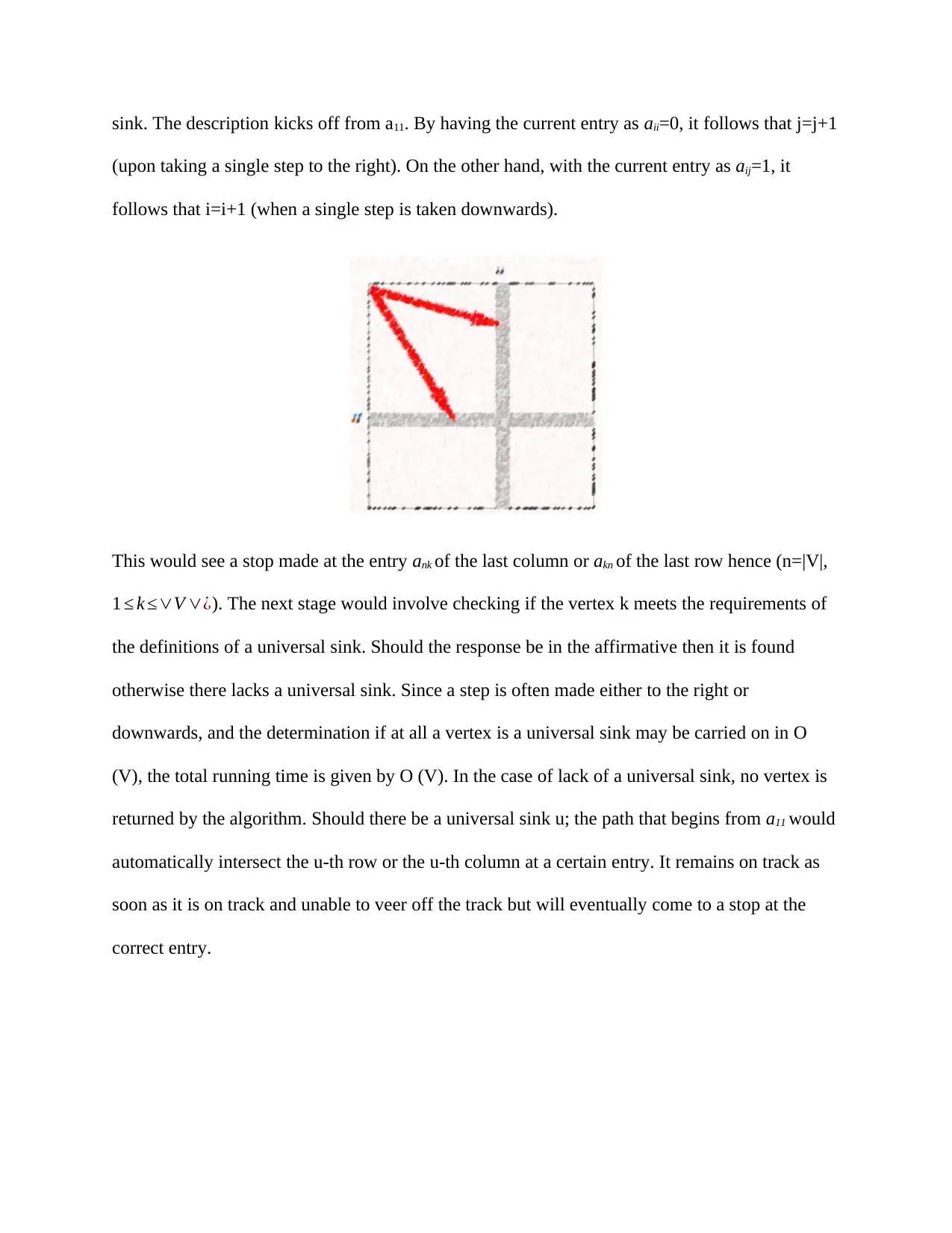
sink. The description kicks off from a11. By having the current entry as aii=0, it follows that j=j+1
(upon taking a single step to the right). On the other hand, with the current entry as aij=1, it
follows that i=i+1 (when a single step is taken downwards).
This would see a stop made at the entry ank of the last column or akn of the last row hence (n=|V|,
1 ≤ k ≤∨V ∨¿). The next stage would involve checking if the vertex k meets the requirements of
the definitions of a universal sink. Should the response be in the affirmative then it is found
otherwise there lacks a universal sink. Since a step is often made either to the right or
downwards, and the determination if at all a vertex is a universal sink may be carried on in O
(V), the total running time is given by O (V). In the case of lack of a universal sink, no vertex is
returned by the algorithm. Should there be a universal sink u; the path that begins from a11 would
automatically intersect the u-th row or the u-th column at a certain entry. It remains on track as
soon as it is on track and unable to veer off the track but will eventually come to a stop at the
correct entry.

References
Kenah, E., Britton, T., Halloran, M. E., & Longini Jr, I. M. (2016). Molecular infectious disease
epidemiology: survival analysis and algorithms linking phylogenies to transmission
trees. PLoS computational biology, 12(4), e1004869
Michu, S., DELHI, A. I., Michu, N., & DELHI, A. I. (2018). Design and analysis of algorithms