Advanced Functions - Equation of Mathews’ gastronomic tract

Running head: ADVANCED FUNCTIONS
ADVANCED FUNCTIONS
Name of the Student
Name of the University
Author Note

Part A: The Anatomy
Question 1:
a) Given, equation of Mathews’ gastronomic tract is
g(x )=−x5 +11 x4 – 43 x3+69 x2 – 36 x
Here, x = distance travelled by the scope
g(x) = vertical height within the body
Now, the equation is written in factored form as given below.
g( x )=−x5 +11 x4 – 43 x3+69 x2 – 36 x
= −x5 +4 x4 +7 x4 – 28 x3−15 x3 +60 x2+ 9 x2 – 36 x
Putting x = 4 in the equation gives g(4) = 0. Hence, x= 4 is a factor
= −(x4)(x – 4)+7 x3 (x−4)−15 x2 ( x−4)+9 x ( x−4)
= ( x – 4 )(−x4 +7 x3−15 x2 +9 x )
= x ( x – 4)(−x3 +7 x2−15 x+9)
= x ( x – 4)(−x3 +3 x2+ 4 x2−12 x−3 x+9)
= ( x – 4 )(−x2 ( x−3 ) + 4 x ( x−3 )−3 ( x−3 ) )
= x ( x – 4)( x −3)(−x2 +4 x−3)
= x ( x – 4 ) ( x−3 ) (−x2+ 3 x +x−3 )
= x ( x – 4 ) ( x−3 ) ¿
= x ( x – 4 ) ( x−3 ) (x−3)(1−x)

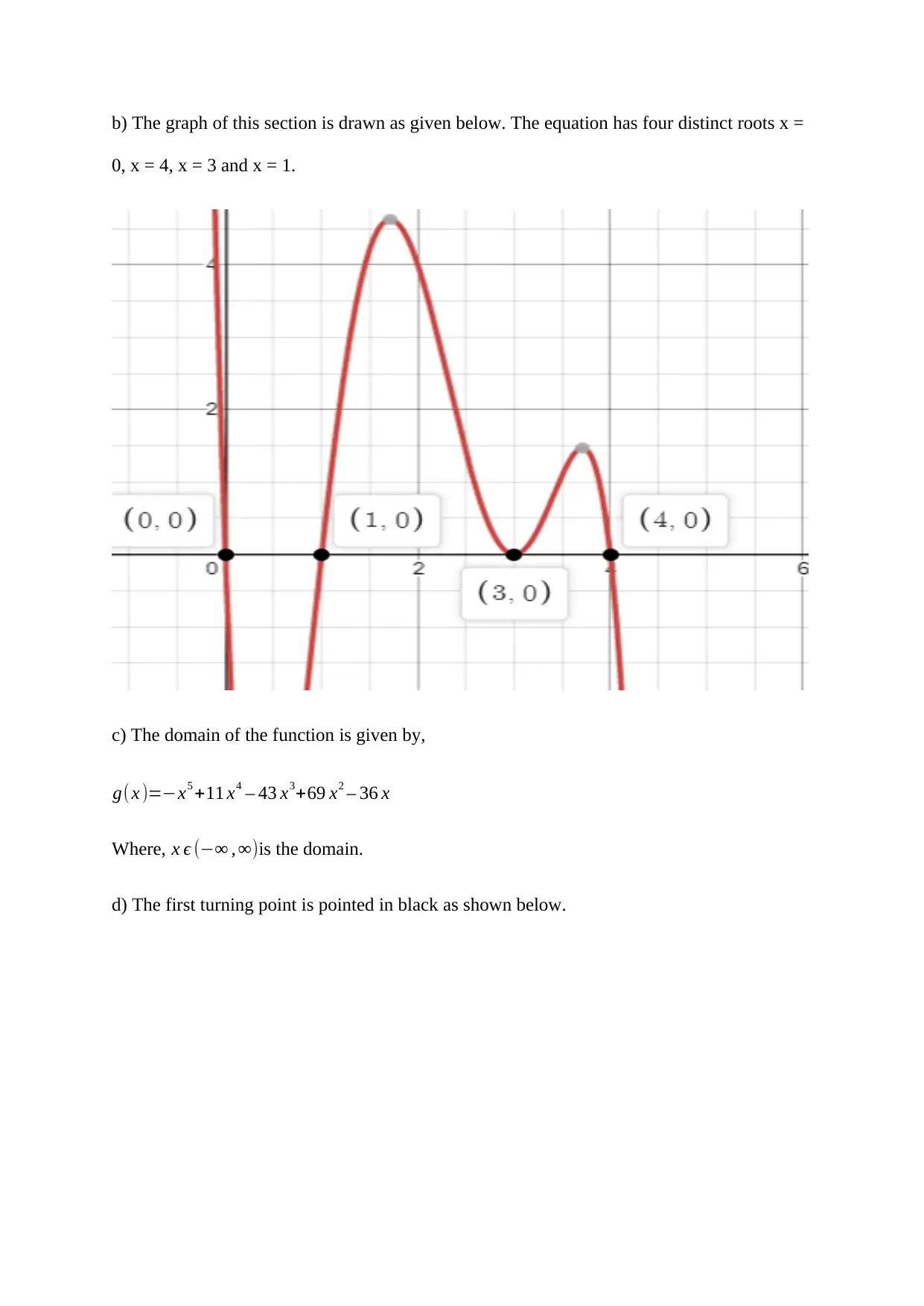
b) The graph of this section is drawn as given below. The equation has four distinct roots x =
0, x = 4, x = 3 and x = 1.
c) The domain of the function is given by,
g( x )=−x5 +11 x4 – 43 x3+69 x2 – 36 x
Where, x ϵ (−∞ , ∞)is the domain.
d) The first turning point is pointed in black as shown below.

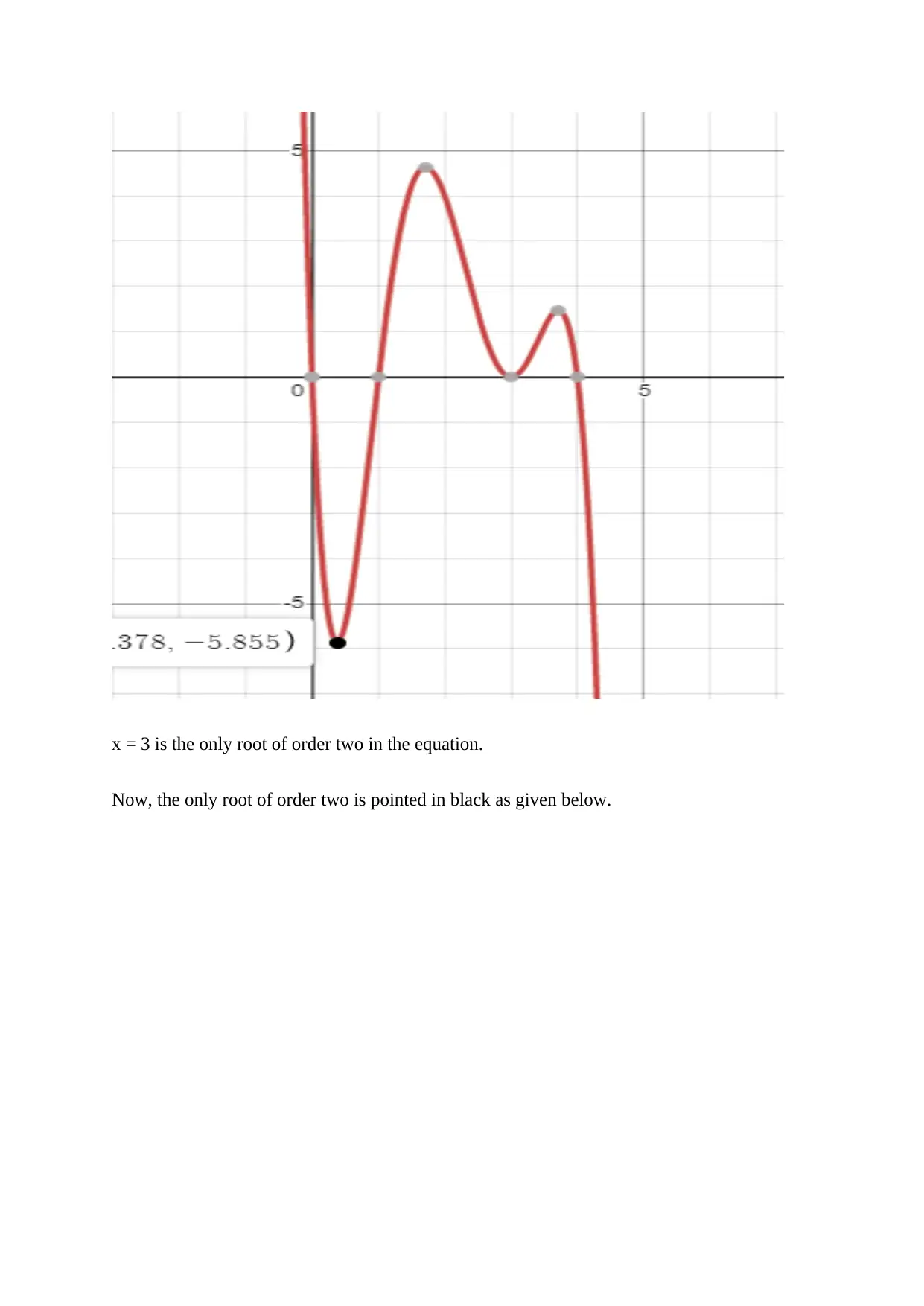
x = 3 is the only root of order two in the equation.
Now, the only root of order two is pointed in black as given below.

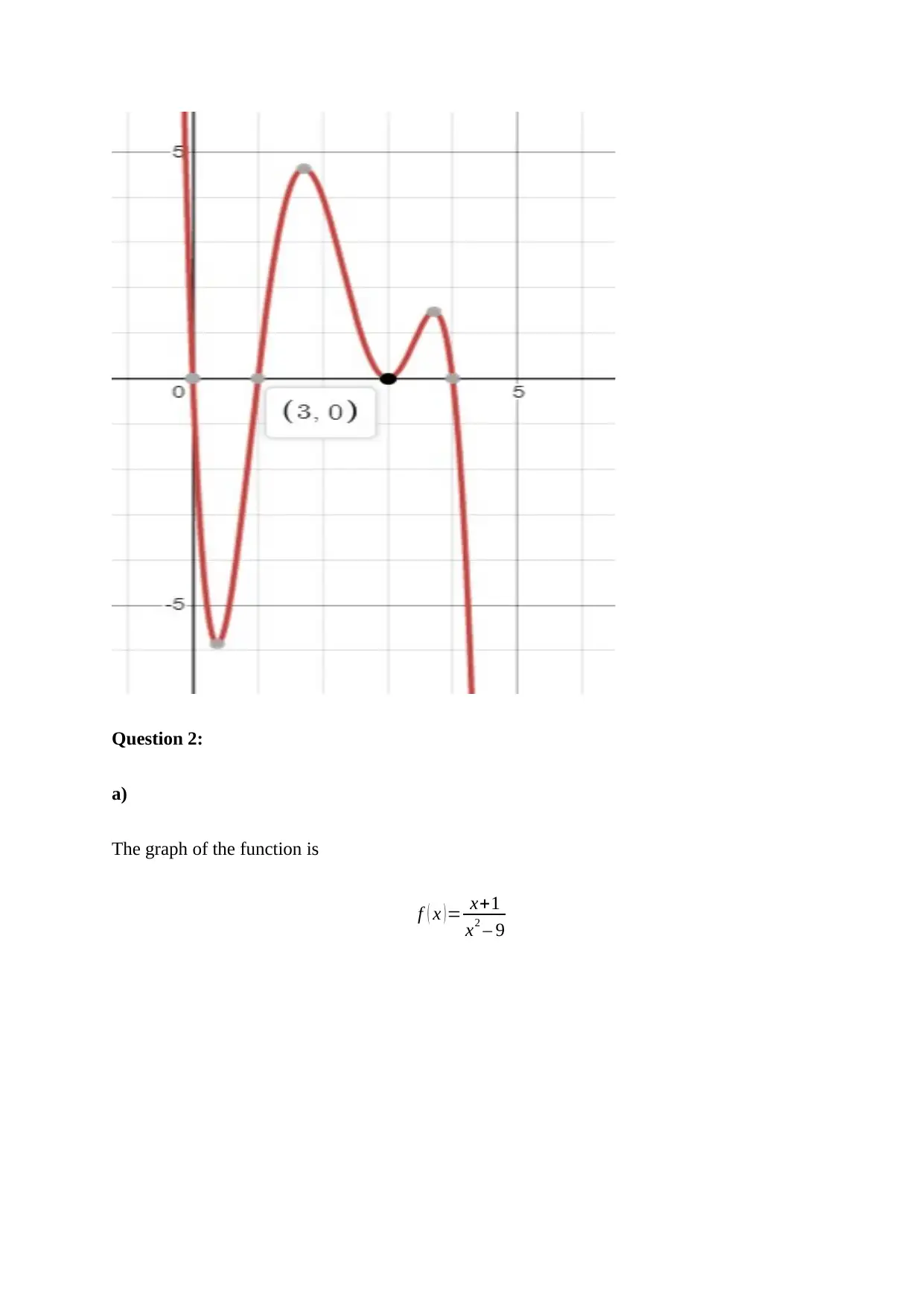
Question 2:
a)
The graph of the function is
f ( x ) = x+1
x2 – 9

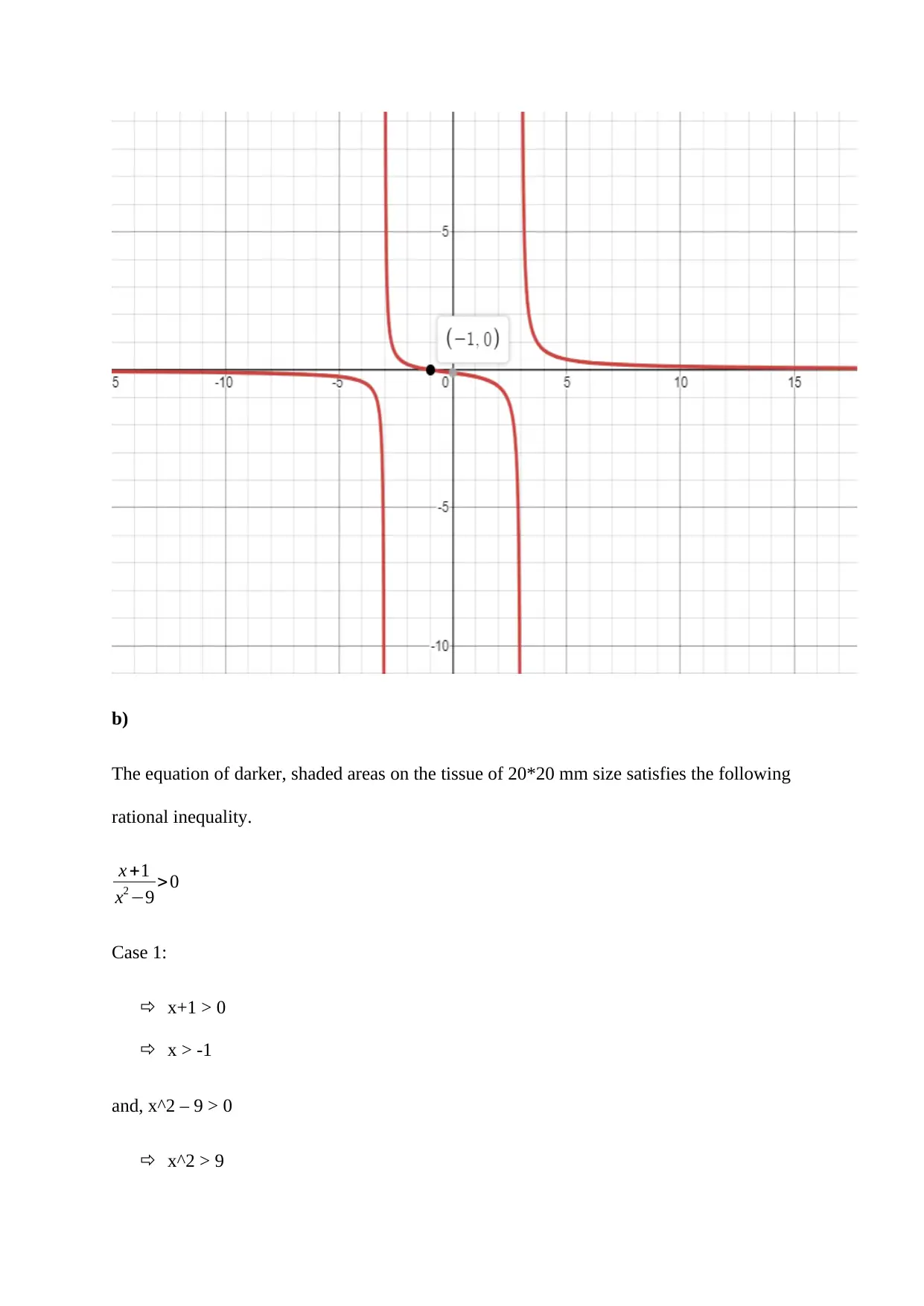
b)
The equation of darker, shaded areas on the tissue of 20*20 mm size satisfies the following
rational inequality.
x +1
x2 −9 >0
Case 1:
 x+1 > 0
 x > -1
and, x^2 – 9 > 0
 x^2 > 9

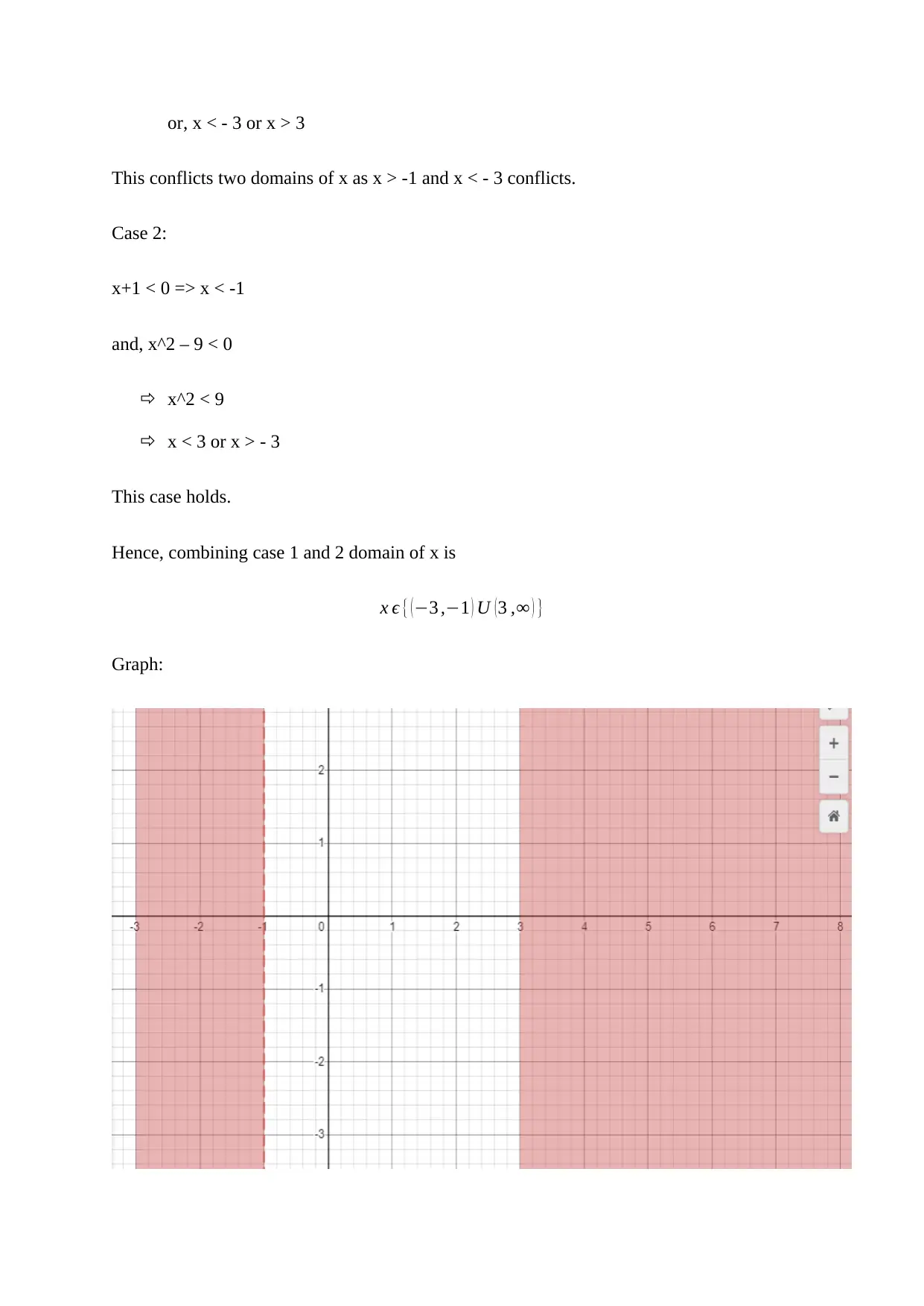
or, x < - 3 or x > 3
This conflicts two domains of x as x > -1 and x < - 3 conflicts.
Case 2:
x+1 < 0 => x < -1
and, x^2 – 9 < 0
 x^2 < 9
 x < 3 or x > - 3
This case holds.
Hence, combining case 1 and 2 domain of x is
x ϵ { (−3 ,−1 ) U (3 ,∞ ) }
Graph:

Part B: The Diagnosis
Question 3:
a) The base function for g(x) is f(x) = sinx
where x = months
Function period = 4 months
Function amplitude = 5
Axis of the function g(x) is y = 5.
Horizontal shifting to right = 2 months.
Now, period of f(x) = sin(x) is 2π. Hence, period of f(kx) = 2π/k.
Now, 2π/k = 4 => k = 2π/4 = π/2.
Hence, equation of the function is
g(x) = 5f((π/2)x-2) + 5
= 5sin((π/2)x-2) + 5
b) The graph of the function g(x) is given below.

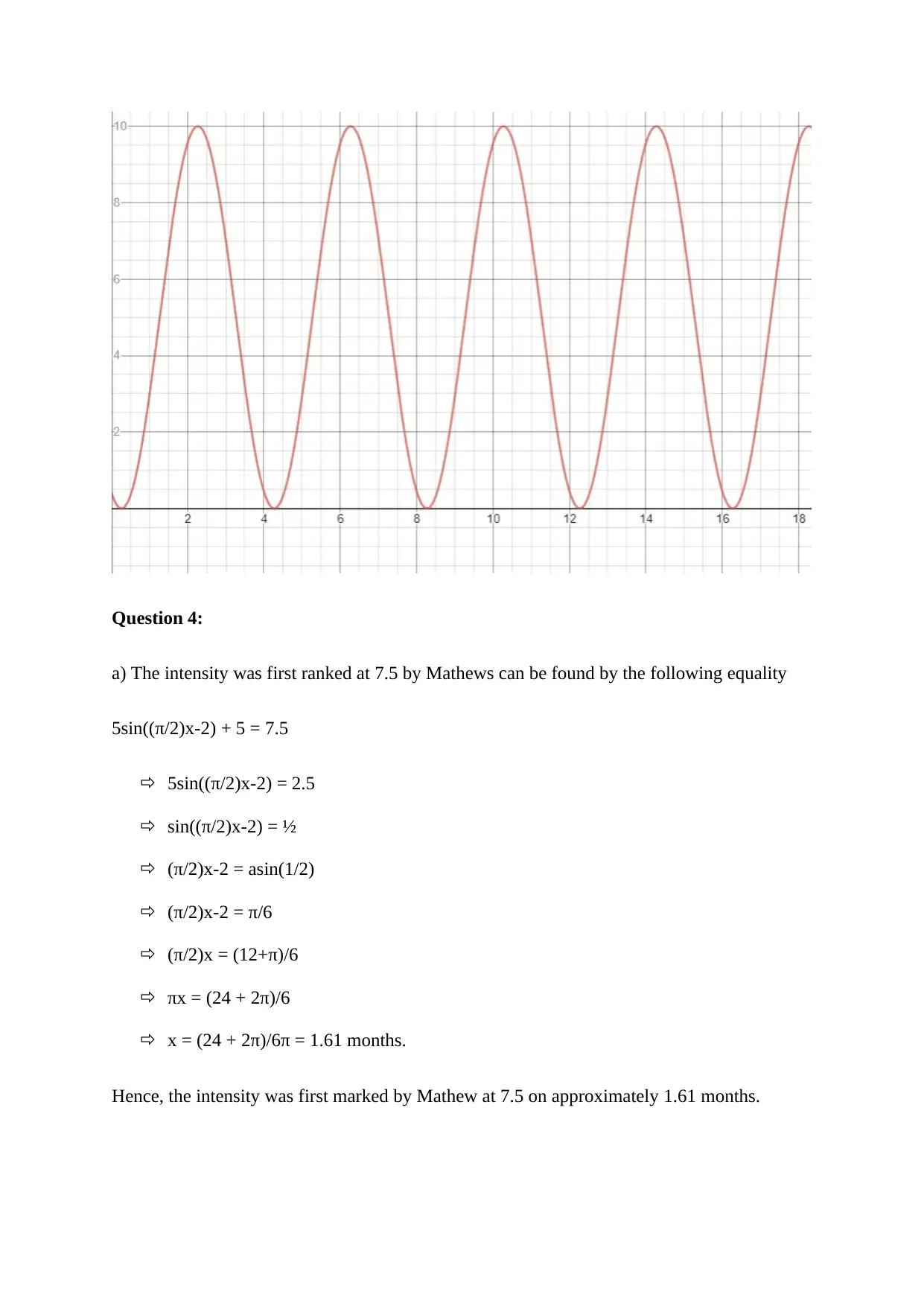
Question 4:
a) The intensity was first ranked at 7.5 by Mathews can be found by the following equality
5sin((π/2)x-2) + 5 = 7.5
 5sin((π/2)x-2) = 2.5
 sin((π/2)x-2) = ½
 (π/2)x-2 = asin(1/2)
 (π/2)x-2 = π/6
 (π/2)x = (12+π)/6
 πx = (24 + 2π)/6
 x = (24 + 2π)/6π = 1.61 months.
Hence, the intensity was first marked by Mathew at 7.5 on approximately 1.61 months.

b) The periodic function has the period of 4 months. Now, if at 1.61 month the intensity was
7.5 for first time then after 4*2 = 8 months the intensity will again be 7.5 for the third time.
Hence, at 1.61 + 8 = 9.61 months the intensity was approximately 7.5 for third time.
c) Now, after 12 months the intensity value can be found by its equation.
g(12) = 5sin((π/2)12-2) + 5 = 0.45.
Hence, after 12 months the intensity value is marked as 0.45.
Part C – The Treatment
Question 5:
a) In 10 hours the population of bacteria gets doubled.
Let, at some time the population of bacteria is b
Hence, after 10 hours population will be 2b.
In 10 hours population is increased by b.
Hence, in 1 hour population is increased by b/10.
Thus exponential growth model of the bacteria can be presented by the following differential
equation.
db ( x )
dx = b
10
 db/b = dx/10
 ∫ db
b =∫ dx
10
 ln ( b ) = x
10 + ln (c )

 ln (b
c )= x
10
 b = c e
x
10
Now, initially b(0) = 10000 per ml.
Hence, 10000 = c
So, b = 10000 e
x
10
b) Now, time in hours when the number of bacteria reaches 100000 per ml can be found by
the following equation.
100000 = 10000 e
x
10
 e
x
10 =10
 x/10 = ln10
 x = 10*ln10 = 23.026 hours.
e) At 20 hours the population is
b(20) = 10000 e
20
10 = 73890.56
Now, at 30 hours the population is
b(30) = 10000 e
30
10 = 200855.369
Hence, the average rate of change = (200855.369 - 73890.56)/(30-20) = 12696.48 per hour
per ml.
f) The instantaneous rate of change at x = 24 hours is given by,
db ( x )
dx ∨x =24=b (24)
10

b(24) = 10000 e
24
10 = 110231.76
Hence, db ( x )
dx ∨x =24 = 110231.76/10 = 11023.176 per ml.
Hence, the instantaneous change in x = 24 hour is 11023.176 per ml.
Question 6:
a) Given the concentration of levofloxacin in mol/L over a time x in hours is given by,
.
Also, the concentration of metronidazole in mol/L over a time x hours is
Now, initially i.e. at time t= 0
C(0) = 5*log(0+1) + 10 = 10 mol/L
And D(0) = 10log(0+1) + 5 = 5 mol/L
Hence, the initial concentration of levofloxacin is higher than initial concentration of
metronidazole.
b) Now, C(x) = D(x) can be found by equating the expressions of both.
5*log(x+1) + 10 = 10log(x+1) + 5
 5*log(x+1) = 5
 log(x+1) = 1
 x+1 = e
 x = e – 1 = 1.718 hours.