Advanced Mathematics Assignment - University Advanced Math Course

This document presents a comprehensive solution to an advanced mathematics assignment. The assignment includes detailed solutions for several key concepts: the Heaviside step function and its graphical representation, including convolution; applying the Fourier transform to solve a differenti...Read More

INSTITUTIONAL AFFILIATION
FACULTY OR DEPARTMENT
COURSE ID & NAME
TITLE:
ADVANCED MATHEMATICS
STUDENT NAME
STUDENT ID NUMBER
PROFESSOR (TUTOR)
DATE OF SUBMISSION

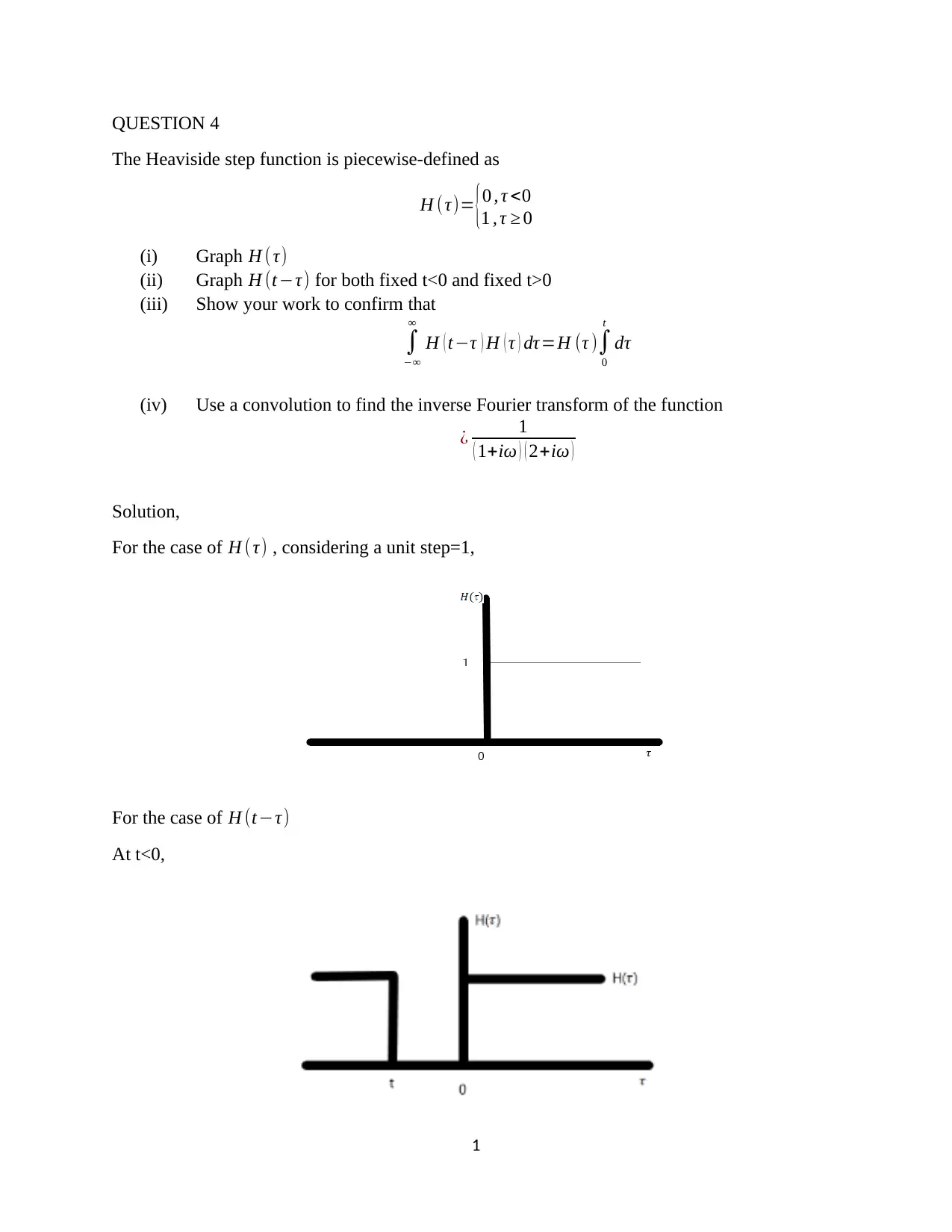
QUESTION 4
The Heaviside step function is piecewise-defined as
H (τ)= {0 , τ <0
1 , τ ≥ 0
(i) Graph H ( τ)
(ii) Graph H (t−τ) for both fixed t<0 and fixed t>0
(iii) Show your work to confirm that
∫
−∞
∞
H ( t−τ ) H ( τ ) dτ=H (τ )∫
0
t
dτ
(iv) Use a convolution to find the inverse Fourier transform of the function
¿ 1
( 1+iω ) ( 2+iω )
Solution,
For the case of H (τ) , considering a unit step=1,
For the case of H (t−τ)
At t<0,
1

At t>0,
The area between 0 and t is of interest to the function.
Therefore,
Convolving the two functions,
∫
−∞
∞
H ( t−τ ) H ( τ ) dτ
The region is under 1 from [0 ,t ].
As a result,
∫
0
t
1∗dτ=∫
0
t
dτ
QUESTION 5
Apply the Fourier transform to the differential equation
y +6y'+5y=δ(t-3
To obtain the solution y=f (t )
Solving the differential equation using Laplace transform
L { y +6 y'+5 y\} =(s^2 +6s+5)Y(s)-y'(0
With no initial boundary conditions, assumption on all to be unity.
( s2 +6 s+5 ) Y ( s )− y' ( 0 ) =0
Let y' ( 0 )=1,
2

( s2 +6 s+5 ) Y ( s )−1=e−cs
Y ( s ) = 1
s2 +6 s +5
Finding the roots,
Y ( s ) = 1
( s +1 ) ( s+ 5 )
On the other hand of the equation,
δ (t−3 )
Using Laplace transformation,
δ (t−3)→ e−3 s
Using the partial fractions,
Y ( s )= a
s +1 + b
s+5
e−3 s =a ( s +5 ) +b ( s+1 )
at s=−1 , 1=a ( 4 ) +b ( 0 )=1
a= 1
4
at s=−5 , 1=a ( 0 )+b (−4 )=1
b=−1
4
Y ( s )= 1
4 ( 1
s+1 )− 1
4 ( 1
s+5 )performing an Inverse Laplace Transform,
Y ( s )=e−3 s
( 1
4 F ( s )− 1
4 G ( s ) )
Solving in time domain,
y ( t ) = 1
4 u3 ( t ) f ( t−3 )−g ( t )
QUESTION 6
3

If f n ( x )=cos ( nπx
L ), what is the value of the inner product ( f n , f n ) with weight ω ( x ) =1 on the
interval (0 , L) for n=0 , 1, 2 , …
Solution
For a norm squared, the inner product is obtained from multiplying the function with
itself, such that,
( f n , f n ) =||f ||
2
=∫
a
b
r ( x ) f 2 ( x ) dx
f n ( x )=cos ( nπx
L )∧r ( x )=w ( x )=1
The interval is given as [0, L]
Therefore,
¿∫
0
L
1∗co s2
( nπx
L ) dx
Integrating a cosine function results in a sinusoidal function which is an orthogonal
function,
Let u=nπx
L → dx= l
πn du
¿ l
πn ∫ co s2 (u ) du
Applying the reduction formula,
∫ co s2 ( u ) du= n−1
n ∫ co sn−2 ( u ) du+ co sn−1 ( u ) sin ( u )
n
Values can be obtained for different values of n.
At n=2,
∫ co s2 ( u ) du= 1
2∫ cos ( 2 u ) du+ 1
2∫ 1 du
Let v=2u → du=1
2 dv
∫ co s2 ( u ) du= 1
2∫ cos ( v ) dv
Replacing in the equation above,
4

∫ co s2 ( u ) du= 1
2 sin ( v )
∫ co s2 ( u ) du= sin ( 2u )
2
Solving for ∫1 du=u
Replacing in the main equation,
l
4 πn ∫ co s2 ( u ) du= l
4 πn sin ( 2 u ) + lu
2 πn
Replacing u=nxπ
l ,
l
4 πn sin ( 2 πnx
l )+ x
2 + C , ∀ :l >0
QUESTION 7
Sturm-Liouville problem on (0 , L),
Part a
The function is given as, X ” ( x ) =−λX ( x ) , 0< x <L
A regular Sturm-Liouville problem is an eigen value problem that has an unknown value. It is
defined as a two-point boundary value problem such that,
p ( x ) y' −q ( x ) y + λr ( x ) y=0 0<x<l
α1 y ( 0 ) +α2 y' ( 0 ) =0
β1 y ( l ) + β2 y' ( l ) =0
p ( x ) >0∧r ( x ) >0
All are S-L variables.
5

Part b
Case: Neumann boundary conditions,
p ( x ) =1 ,q ( x ) =0 , r ( x ) =1
Part b & Part c
The eigen values are
λn= n2 π2
L2
The eigen functions are
yn ( x )=sin (nπ
L x)
Supposing that p ( x ) , p' ( x ) , q ( x ) ,∧r ( x ) are continuous on [a,b] and suppose p ( x )> 0 and r ( x )>0
for all x ∈[a , b]. Then the Sturm-Liouville regular problem has an increasing sequence of eigen
values such that,
λn=λ1 > λ2> λ3
lim
n → ∞
λn =+∞
All the eigenvalues are non-negative as predicted by the theorem. λn is a constant multiple of a
single eigenfunction yn ( x ). Further, the general solution is given as,
6

X ( x )= Acos ( √ λ x )+Bsin ( √λ x ) if λ> 0
X ( x )= Ax+B if λ=0
To satisfy, hB−A=0 , A=0 , hence B=0
note :(h> 0)
λ=0 , not an eigenvalue →no eigenfunction(no nonzero solution )
Part d
Testing for λ> 0
Using the boundary conditions,
0=hA− √ λ B
0=− A √ λ sin ( √ λ ) +B √λ cos ( √ λ )
At A=0 , B=0 hence both are non-zeros.
B= hA
√ λ ∧0=− A √λ sin ( √λ )+ hA
√ A √λ cos ( √ λ )
A ≠ 0 ( solution would be toolarge )
0=− √ λ sin ( √ λ ) +h √ λ cos ( √ λ )
h
√ λ =tan √ λ
Part e
The appropriate eigen function, assuming A=1, B= h
√ λ
Such that,
X n ( x )=cos ( √ λn x )+ h
√ λn
sin ( √ λn x )
Part f
7

The sin nx terms of the function are orthogonal for distinct n on the range [ 0 , π ]. The r ( x ) term is
the weight function on [a , b]. The orthogonality of a function is based on the weight function,
r ( x ). The inner product is given as,
⟨ f |g ⟩ ¿
¿∫
a
b
f ( x ) g ( x ) r ( x ) dx
8