Advanced Water Engineering: Energy Depth Relationship in Open Channel Flow

This article discusses the energy depth relationship in open channel flow in Advanced Water Engineering. It explains the Bernoulli's equation and the E-Y diagram. The article also covers subcritical flow, critical depth, and the effect of hump height on flow depth.

ADVANCED WATER ENGINEERING
[Author Name(s), First M. Last, Omit Titles and Degrees]
[Institutional Affiliation(s)]

E1: The flow is subcritical
The total energy here remains constant but the flow per unit width changes
q p= Q
B1
qQ= Q
B2
; Hence B1>B2
and q p <qQ
So as the flow width increases at a particular specific energy, the depth value decreases as shown
in the figure
q=flow over unit width
q1> q2 >q3

It is different from E2 since in E2 the flow over the depth does not change the specific energy but
here specific energy does not change while there is a change in the flow over the width. Still, this
is a subcritical flow because V (wave velocity) < C0 (wave celerity) and under this condition the
wave will travel in the upstream direction. Hence, F= V
C0
, Fr < 1 (where Fr is the Froude
number) (Hager & Castro-Orgaz 2015).
E2: Energy depth relationship in a rectangular channel
In open channel flow, the specific energy is the energy drops relative to the channel bottom. The
specific energy is expressed in terms of kinetic energy and potential energy and total energy
(Kabiri-Samani, Bakhshian & Chamani 2017). The Bernoulli’s equation which originates from a
control volume analysis is used in the description of the specific energy relationships in fluids.
The three components of energy in Bernoulli’s equation are density, pressure and velocity. The
velocity of the flow is linear and the depth of the flow can be determined using the equation
v1
2
2 g + y1 + P1
r −hp = v2
2
2 g + y2+ P2
r (Viero & Defina 2017)
Where y is the vertical distance
P=pressure
V= velocity
Hp=head pressure due to friction
r=the specific weight of the fluid; and
g=the acceleration due to gravity

The E-Y diagram is as shown in the figure below
As can be observed in the diagram, for a specific discharge, the specific gravity can be calculated
and can be plotted in the E-Y diagram
Where q=Q/b Q=volumetric discharge
b=base width of the rectangular channel
q= unit discharge
Total Energy, E= Q2
εg y2 + y
E3: An increase in the hump height leads to a corresponding decrease in the depth of flow until a
stage reaches y2=yc which is the critical depth. At this depth
y2=yc
E2= Ec= yc + Q2
2 g B2− y2
2
∆z=∆z max
By increasing the height of the pump beyond ∆z max, say ∆z’, where ∆z’>∆z max, it is clear that
the specific energy available at secn1 will increase to E1
1so that

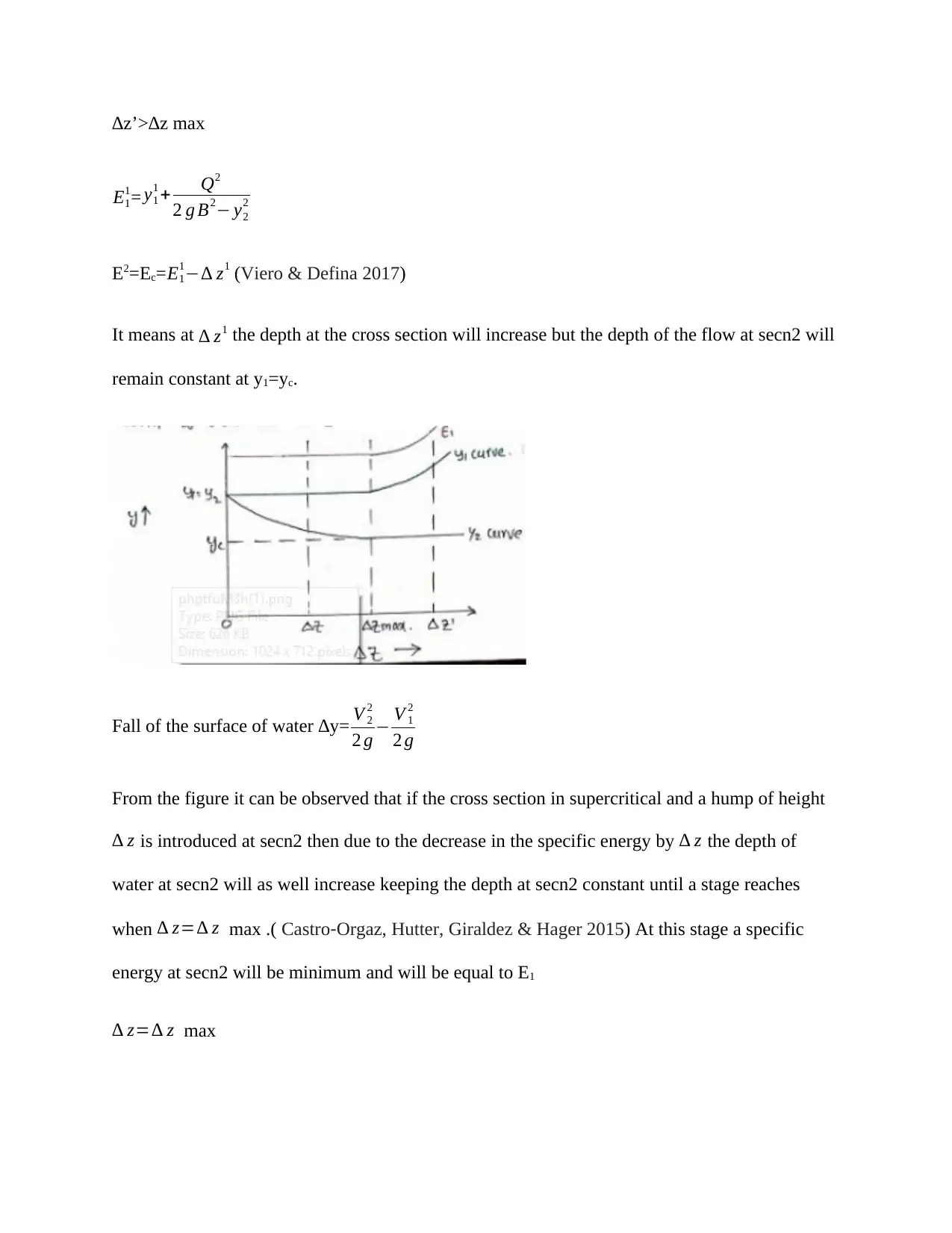
∆z’>∆z max
E1
1= y1
1 + Q2
2 g B2− y2
2
E2=Ec=E1
1−∆ z1 (Viero & Defina 2017)
It means at ∆ z1 the depth at the cross section will increase but the depth of the flow at secn2 will
remain constant at y1=yc.
Fall of the surface of water ∆y= V 2
2
2 g − V 1
2
2 g
From the figure it can be observed that if the cross section in supercritical and a hump of height
∆ z is introduced at secn2 then due to the decrease in the specific energy by ∆ z the depth of
water at secn2 will as well increase keeping the depth at secn2 constant until a stage reaches
when ∆ z=∆ z max .( Castro‐Orgaz, Hutter, Giraldez & Hager 2015) At this stage a specific
energy at secn2 will be minimum and will be equal to E1
∆ z=∆ z max

E2= Ec= yc + Q2
2 g B2− yc
2
Ec=1.5 yc
E2= Ec=E1−∆ z max
E1= yc= y1+ Q2
2 g B2 − y1
2
Up to this points, depth at secn1 will be unchanged but its hump but is further increased beyond
∆z max, say ∆z’ then at this available specific energy flow will not be possible to maintain the
flow, depth at the cross section side will reduce to increase the SE at secn1 from E1 to E1’ such
that
∆z’> ∆z max
E2= Ec= yc + Q2
2 g B2− y1
2
E1
1=Ec+∆ z'
E1
1= y1
1+ Q2
2 g B2− y1
2
E4: Consider a horizontal frictionless rectangular channel of width b carrying a discharge a at a
depth y1
The loss below section 1 and 2; construction of hump causes specific energy at section 2 to
decrease by ∆z

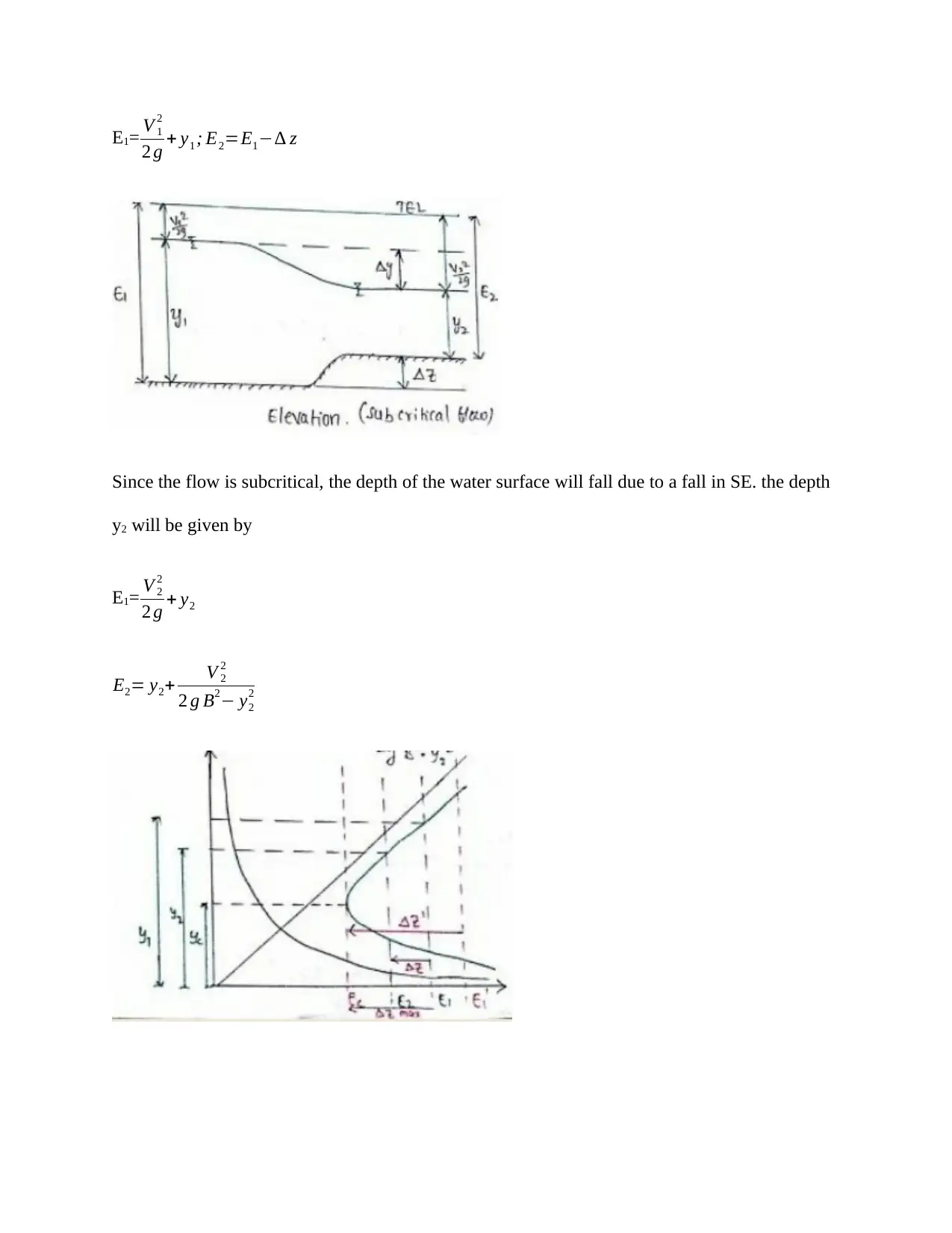
E1= V 1
2
2 g + y1 ; E2=E1−∆ z
Since the flow is subcritical, the depth of the water surface will fall due to a fall in SE. the depth
y2 will be given by
E1= V 2
2
2 g + y2
E2= y2+ V 2
2
2 g B2− y2
2

References
Castro‐Orgaz, O., Hutter, K., Giraldez, J. V., & Hager, W. H. (2015). Nonhydrostatic granular
flow over 3‐D terrain: New Boussinesq‐type gravity waves. Journal of Geophysical
Research: Earth Surface, 120(1), 1-28
Hager, W. H., & Castro-Orgaz, O. (2015). Transcritical flow in open channel hydraulics: From
Böss to De Marchi. Journal of Hydraulic Engineering, 142(1), 02515003
Kabiri-Samani, A. R., Bakhshian, E., & Chamani, M. R. (2017). Flow characteristics of grid
drop-type dissipators. Flow Measurement and Instrumentation, 54, 298-306
Viero, D. P., & Defina, A. (2017). Extended Theory of Hydraulic Hysteresis in Open-Channel
Flow. Journal of Hydraulic Engineering, 143(9), 06017014