Algebra Homework: Analyzing Functions, Lines, and Regression Analysis
VerifiedAdded on 2021/09/10
|8
|685
|28
Homework Assignment
AI Summary
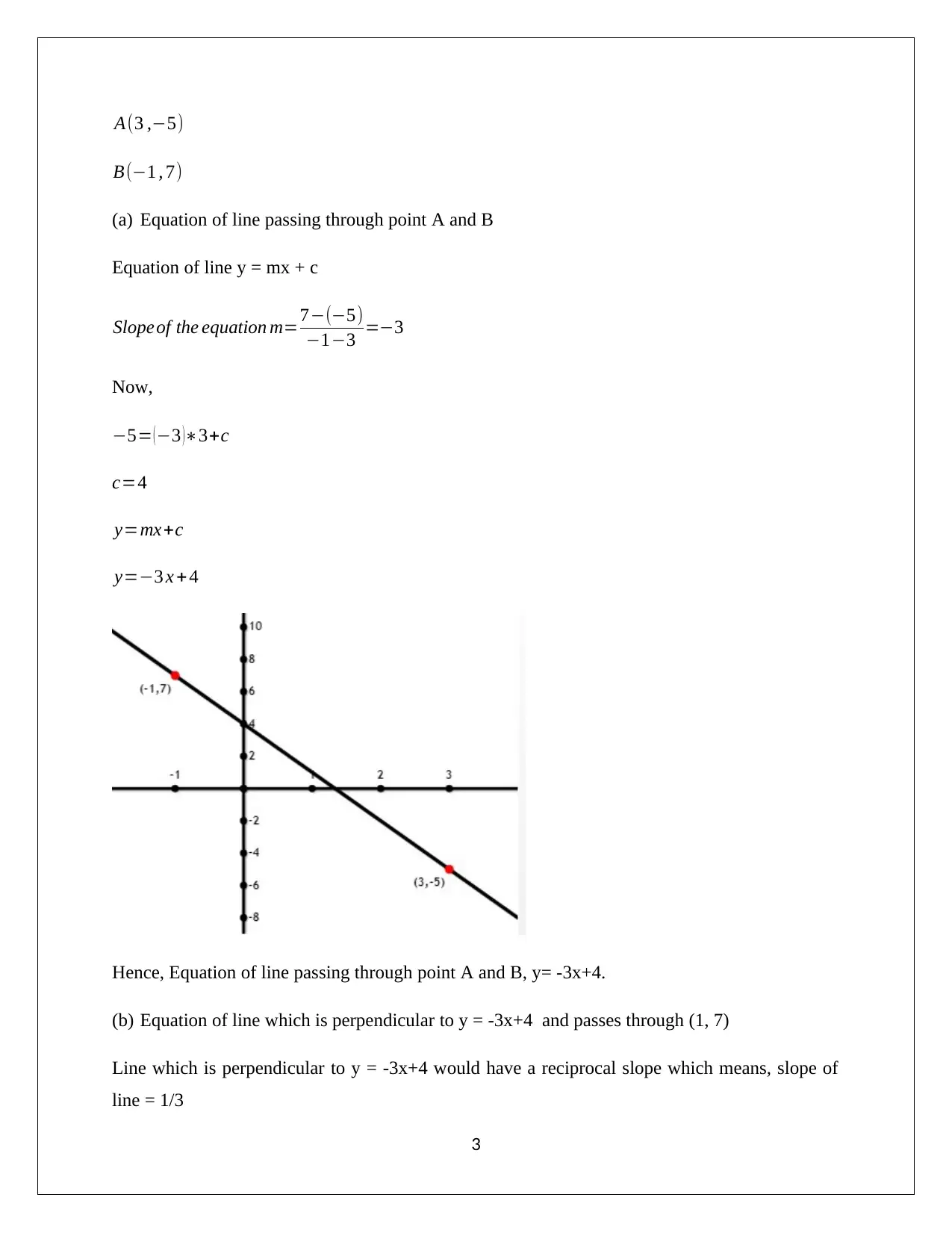
This document presents a comprehensive solution to an algebra homework assignment. It addresses various topics including piecewise functions, graphing functions, determining whether functions are even or odd, finding x and y intercepts, and analyzing the domain and range of functions. The solution also covers linear equations, including finding the equation of a line given points, and determining the equation of a perpendicular line. Furthermore, the assignment explores real-world applications through a word problem involving a phone bill calculation. Finally, it delves into regression analysis, including the calculation of the least squares regression line, correlation coefficient, and interpretation of the slope, demonstrating a strong understanding of algebraic concepts and their applications. This assignment is contributed by a student to be published on the website Desklib. Desklib is a platform which provides all the necessary AI based study tools for students.
1 out of 8














![[object Object]](/_next/static/media/star-bottom.7253800d.svg)