CP5602 Algorithm Analysis Assignment: Data Structures and Algorithms
VerifiedAdded on 2023/06/03
|15
|1404
|218
Homework Assignment
AI Summary
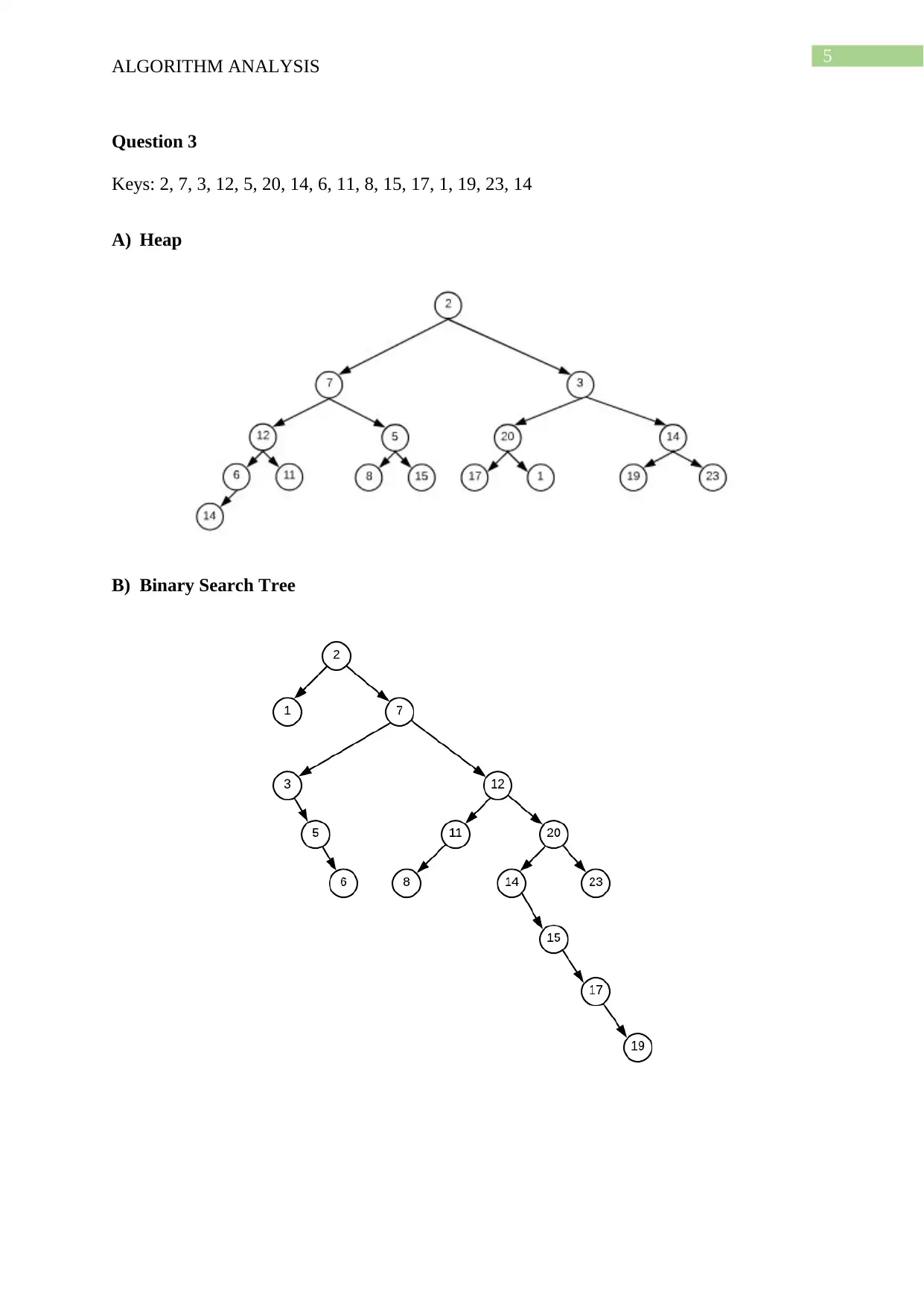
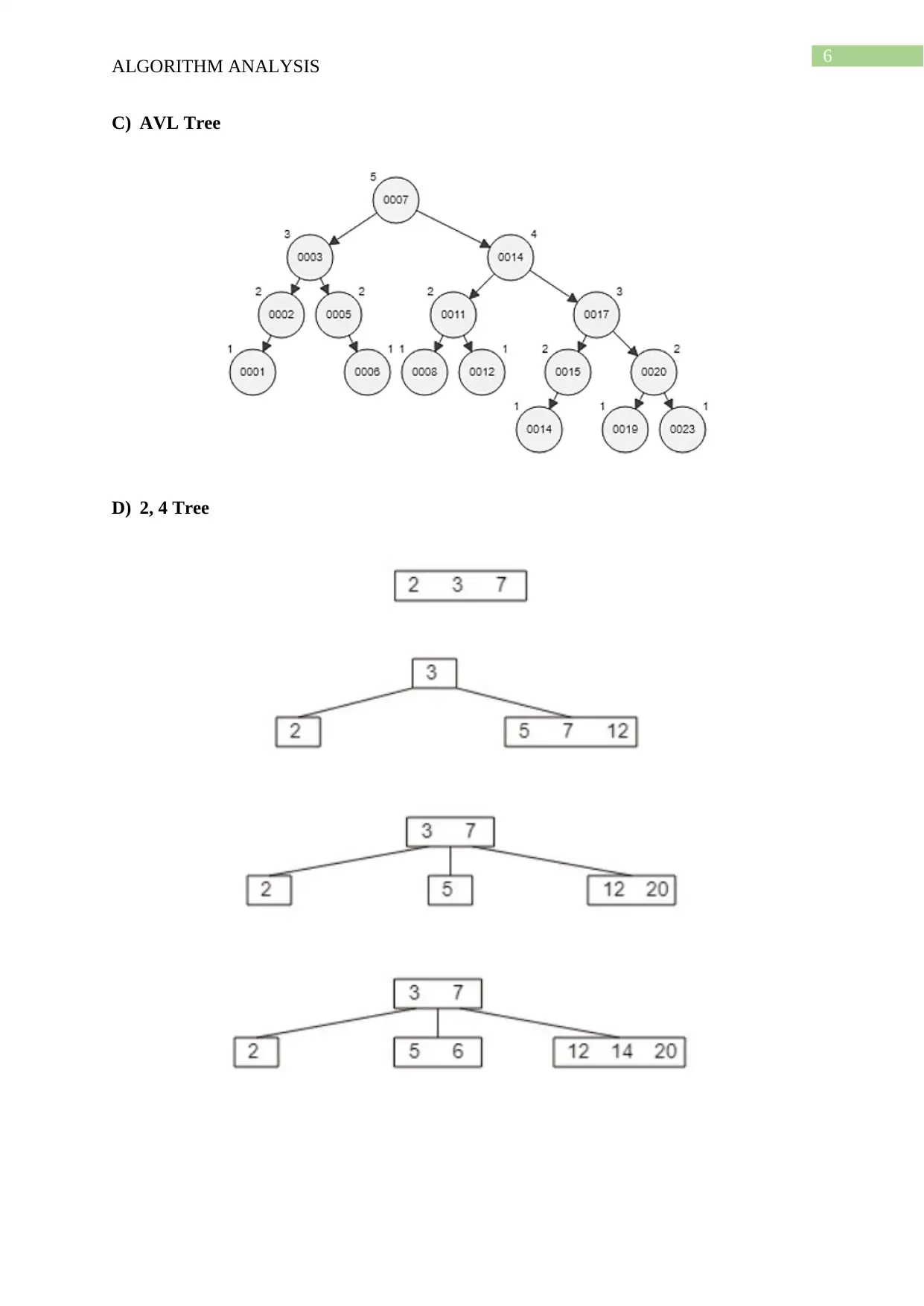
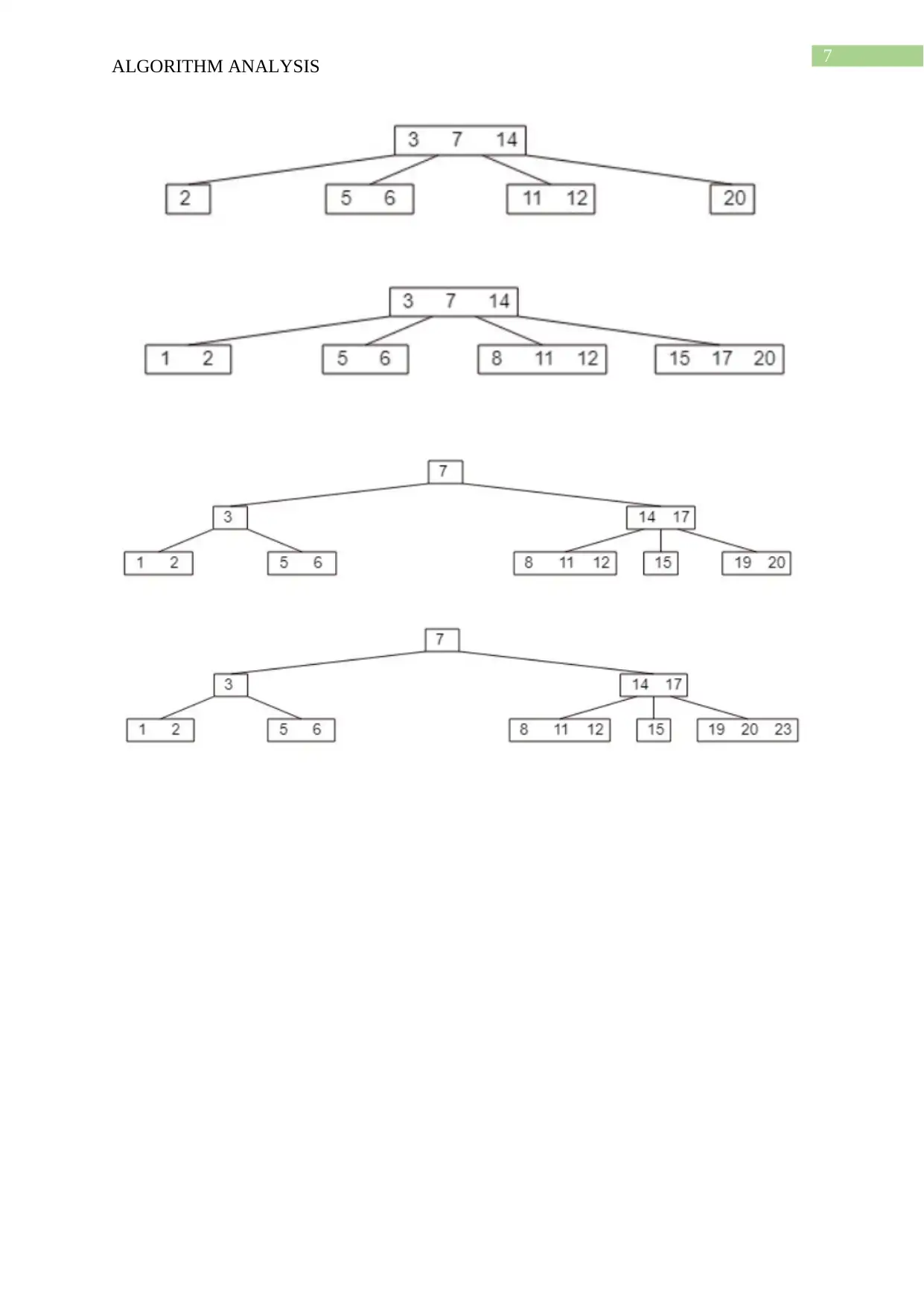
This document presents a comprehensive solution to an algorithm analysis assignment, covering various topics including iterative and recursive binary search algorithms with complexity analysis, different hashing techniques such as separate chaining, linear probing, quadratic probing, and secondary hashing, along with their implementations. It also delves into data structures like heaps, binary search trees, AVL trees, and 2-4 trees, illustrating their construction with a given set of keys. Furthermore, the solution includes finding the Longest Common Subsequence (LCS) of two arrays and determining the optimal matrix chain order using dynamic programming. Lastly, it analyzes string searching algorithms like brute-force, Boyer-Moore, and Knuth-Morris-Pratt, and determines if a given graph is strongly connected using transitive closure. Desklib offers a wide range of solved assignments and study materials to support students in their academic endeavors.
1 out of 15
















![[object Object]](/_next/static/media/star-bottom.7253800d.svg)