Algebraic Solutions to the Questions

This document provides algebraic solutions to various questions. It includes solving equations, finding curves, and analyzing data points. Study material for algebraic solutions is available on Desklib.

ALGREBRAIC SOLUTIONS TO THE QUESTIONS
PART A
QN 1. For this question, we use the theorems provided in the question hence:
(a) Given P= P11 0.2 P13
P21 0.7 P23
P31 0.1 P33
Let state matrix be Q such that if:
Understocked, Q1= 0.7
0.2
0.1
If stocked, Q2= 0.2
0.7
0.1
If overstocked, Q3= 0.4
0.4
0.2
Therefore the possible future states are determined as follows:
Let future states be denoted as F:
(i) So if understocked in the previous week, F1= P11 0.2 P13 0.7
P21 0.7 P23 0.2
P31 0.1 P33 0.1
0.7P11+0.04+0.1P13
= 0.7P21+0.14+0.1P23
0.7P31+0.01+0.1P33

(ii) And if stocked the previous week, F2= P11 0.2 P13 0.2
P21 0.7 P23 0.7
P31 0.1 P33 0.1
(0.2P11+0.14+0.1P13)
= (0.2P21+0.49+0.7P23)
(0.1P31+0.01+0.1P33)
(iii) And if overstocked the previous week, F3= P11 0.2 P13 0.4
P21 0.7 P23 0.4 =
P31 0.1 P33 0.2
= (0.4P11+0.08+0.2P13)
(0.4P21+0.28+0.2P23
(0.4P31+0.04+0.2P33)
This is a Markov chain matrix since all entries in the system state matrix are positive
(b) X(0) = 0
1
0
Given theorem 2: X(1)= P11 0.2 P13 0
P21 0.7 P23 1
P31 0.1 P33 0

= 0.2P11+0.14+0.1P13
0.2P21+0.49+0.1P23
0.2P31+0.07+0.1P33
X(2) = P11 0.2 P13 0.2P11+0.14+0.1P13
P21 0.7 P23 0.2P21+0.49+0.1P23
P31 0.1 P33 0.2P31+0.07+0.1P33
Hence this is reached at the 2nd week
2. (a) Given P= P11 0.2 P13
P21 0.7 P23
P31 0.1 P33
(I-P)q= 0
I= 1 0 0
0 1 0
0 0 1
Let q = X1
X2
X3

1 0 0 P11 0.2 P13
0 1 0 - P21 0.7 P23 = 0
0 0 1 P31 0.1 P33
1-P11 -0.2 -P13 X1
P21 0.3 -P23 X2 = 0
-P31 -0.1 1-P33 X3
(b) If the elements of the state transition matrix above were known then we could determine
the state vector easily
PART B:
QN1: (a) The given equation is: y=ax2+bx+c
Now in order to determine the equation above, the given points within the curve are used:
That is: (0,7), (1,9), (3,19), (6,49)
When x=0, y= a(0)2+b(0)+c = 7 hence c= 7
X=1, y=9: 9= a+b+c……(ii)
X=3, y= 19: 19= 9a+3b+c…..(iii)
X=6, y= 49
49=36a+6b+c……(iv)
Subtracting equation (iii) from (iv), results in: 30= 27a+3b…..(v)
From equation (ii): 9= a+b+7->a=2-b…..(vi)
Substituting equation (vi) into (v), we have : 27(2-b)+3b= 30
54-27b+3b=30
-24b=-24, b= 1 and a=2-1= 1
Therefore the equation is determined as: y= x2+x+7

(b) y= acos(πx)+bsin(πx ¿
Randomly selecting the points should actually conform with the above equation hence say we
choose: (0,1): substituting in the above equation: 1= acos0+bSin 0 ; a=1
Trying another given point: (10,1): 1= acos10π+bSin 10π; a= 1
Therefore can be determined thereafter as follows:
Use point (6,1): 1= Cos 6π+bSin 6π
Hence : b= (1-Cos 6π)/Sin 6π; giving b as infinity ( extremely large number)
Hence y= Cos (πx)+ϛSin (πx)
QN2.
(a) Y= 6-9x+3x2
(0,6): Substituting in the above equation: 6= 6-9(0)+3(0)2, confirmed to be true
(1,0), 0= 6-9+3(1) confirmed to be true
(2,0) , 0 = 6-9x2+3x22 also confirmed to be true
Therefore all points fit in the curve
(b) (3,4), 4= 6-9(3)+3(3)2, 4= 6-27+27 (the 4th point not fitting)
(c) Y=ax2+bx+c (0,6), (1,0), (2,0) and (3,4)
6 = c…..(i)
Substituting the rest: 0 = a+b+c, a= -b-6…(ii)
0 = 4a+2b+c, 4a+2b+6= 0, 2a+b= -3
Substituting (ii) into (iii): 2(-b-6)+b=-3
Suppose we use the point (3,4): 4= 9a+3b+6
9a+3b=-2
9(-b-6)+3b=-2
-9b-54+3b= -2
-3b=-52(+2), b= 18
Therefore y= -24x2+18x+6
QN 3. (a) a (x2+y2) + bx +cy= 1

(-1,0.5): a(1+0.25)-b+0.5c= 1
1.25a-b+ 0.5c= 1 ….(i)
(-0.5,0.5); a(0.5)-0.5b+0.5c = 1
0.5a-0.5b+ 0.5c = 1……(ii)
(0.3,-0.4); a(0.32+0.42)+0.3b-0.4C = 1
0.25a+0.3b-0.4c =1……(iii)
The corresponding system of matrices includes:
1.25 -1 0.5 a 1
0.5 -0.5 0.5 b = 1
0.25 0.3 0.4 c 1
The equation to solve the above is given by:
AtAc= Atb
Let A= 1.25 -1 0.5 a 1
0.5 -0.5 0.5 b = 1
0.25 0.3 0.4 c 1
At= 1.25 0.5 0.25
-1 -0.5 0.3
0.5 0.5 0.4
AtA= 1.25 0.5 0.25 1.25 -1 0.5
-1 -0.5 0.3 0.5 -0.5 0.5
0.5 0.5 0.4 0.25 0.3 0.4
Atb= 1.25 0.5 0.25

-1 -0.5 0.3
0.5 0.5 0.4
= 2
-1.2
1.4
Hence c= (AtA)-1Atb
=
The error becomes: e= (b-Ac)
(same answer as the previous method)
(b) (-1,1), (1.3,1), (0.7,0) and (-0.8,0.8)
1= a(x2+y2)+ bx+cy
1= a(2)-b+c
2a-b+c= 1…..(i)
1= a(1.32+1)+1.3b+c
2.69a+ 1.3b+c= 1…..(ii)
1= a(0.72+0)+0.7b+0.49a+0.7b= 1
1= a(0.82+0.82)-0.8b+0.8c
1= 1.28a-0.8b+0.8c…..(iii)
Subtracting eqn (i) and (ii): 2a-b+c = 1
2.69a+1.3b+c= 1
The system of matrix is given by:

2 -1 1 a 1
2.69 1.3 1 b 1
1.28 -0.8 1 c 1
At= 2 2.69 1.28
-1 1.3 -0.8
1 1 1
AtA= 2 2.69 1.28 2 -1 1
-1 1.3 -0.8 2.69 1.3 1
1 1 1 1.28 -0.8 1
Atb= 2 2.69 1.28 -1
-1 1.3 -0.8 1
1 1 1 1
= 5.97
- 0.5
3
Hence c= (AtA)-1Atb
=
The error becomes: e= (b-Ac)
(Same answer as the previous method)
(c)The latter curve is slightly different from the former.

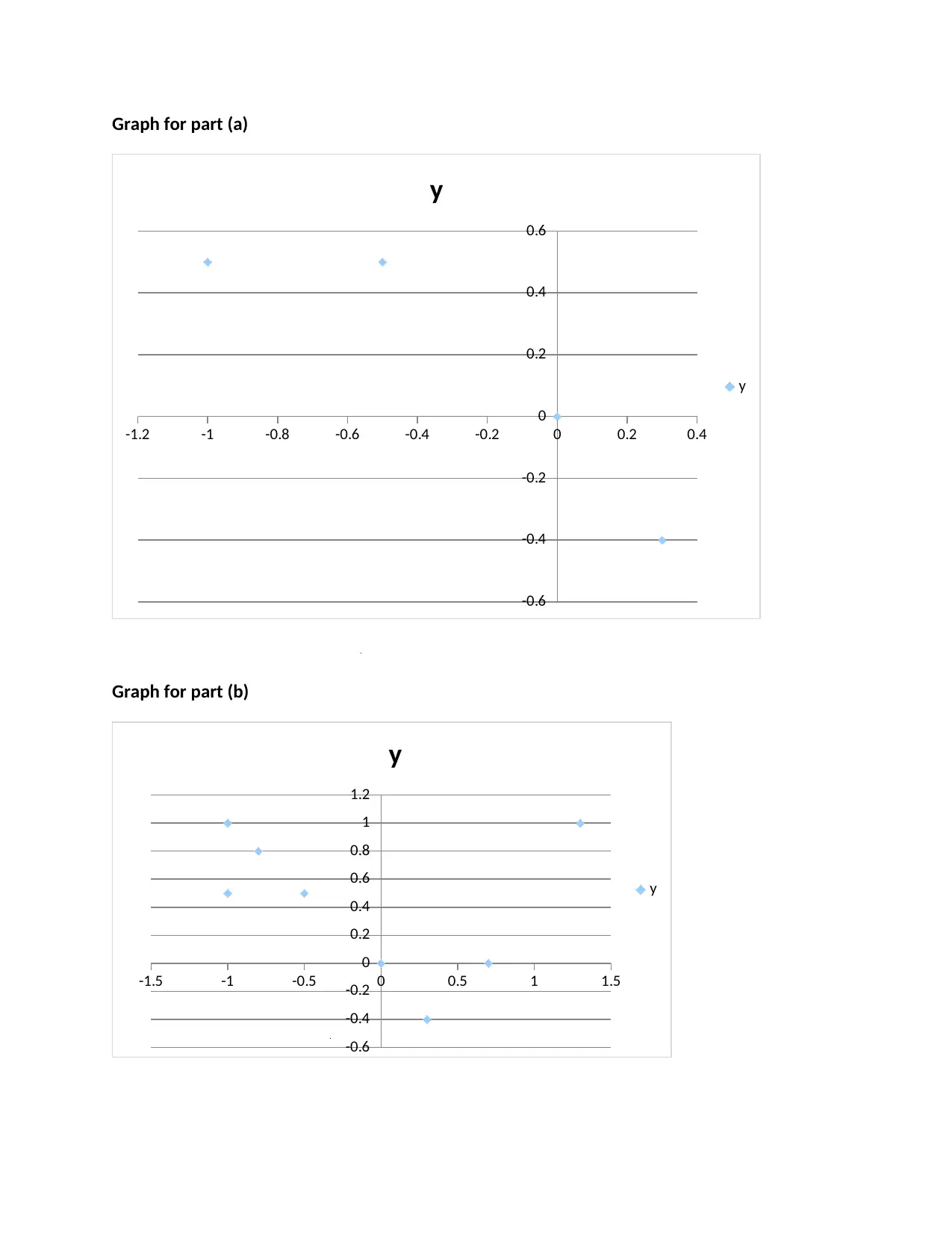
Graph for part (a)
-1.2 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
y
y
Graph for part (b)
-1.5 -1 -0.5 0 0.5 1 1.5
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
1.2
y
y

The shape-factor in the two curves differs greatly as illustrated. The more data points we have
in the curve, the more accurately fitting is the curve.
Qn 4) From the given equation in qn 3 above, we can deduce the following system of equations:
x y x2 y2 x2+y2
-2.241 3.561 5.02208
1
12.6807
2 17.7028
2.46 6.313
6.0516
39.8539
7
45.9055
7
11.365 5.985 129.163
2
35.8202
3
164.983
5
16.971 2.836 288.014
8
8.04289
6
296.057
7
19.72 -1.418 388.878
4
2.01072
4
390.889
1
17.507 -7.807
306.495
60.9492
5
367.444
3
7.03 -9.998
49.4209 99.96
149.380
9
1.9 -8.226
3.61
67.6670
8
71.2770
8
3.111 -3.267 9.67832
1
10.6732
9
20.3516
1
17.7028a-2.241b+3.561c = 1 ….(i)
45.90557a+2.416b+6.313c = 1 …… (ii)
390.8891a+19.72b-1.418c= 1 ….. (iii)
367.4443a+17.507b-7.807c = 1 …..(iv)
The four equations above are necessary and sufficient to determine the three unknowns and
this is achieved as follows:

By Guassian elimination, the unknown constant b can be eliminated for now so as to remain
with only two unknowns for the purpose of finding the solutions:
Hence : 42.77a-5.414b+8.6034c= 2.416 +
102.87a+5.414b+14.147c= 2.241
145.64a+22.7504c= 4.657 ….(v)
6843.295a+345.23b-24.824c = 17.507 -
7245.91a+345.23b-153.954c = 19.72
402.615a-129.13c = 2.213…(vi)
145.64a+22.7504c= 4.657 x 402.615
402.615a-129.13c = 2.213 x 2.213
-> 58636.84a+9159.65c = 1874.98 -
58636.84a- 18806.49= 322.301
C = 1552.679/9646.84 = -0.16095
145.64a= 4.657-22.7504x-0.16095
a = 8.31867/145.64= 0.05711
17.7028x0.05711-2.241xb+3.561x-0.16095
Hence b= -0.573/2.24= -0.256
Therefore the equation that best fits: 0.05711(x2+y2)-0.256x-0.16095y = 1
4b) Given the unknown: 1= Ax2+Bxy+Cy2+Dx+Ey
Using excel, we generate the system of equations as illustrated below:
x Y x2 xy y2
-2.241 3.561 5.022081 -7.9802 12.68072
2.460 6.313 6.0516 15.52998 39.85397
11.365 5.985 129.1632 68.01953 35.82023
16.971 2.836 288.0148 48.12976 8.042896
19.720 -1.418 388.8784 -27.963 2.010724
17.507 -7.807 306.495 -136.677 60.94925
7.030 -9.998 49.4209 -70.2859 99.96

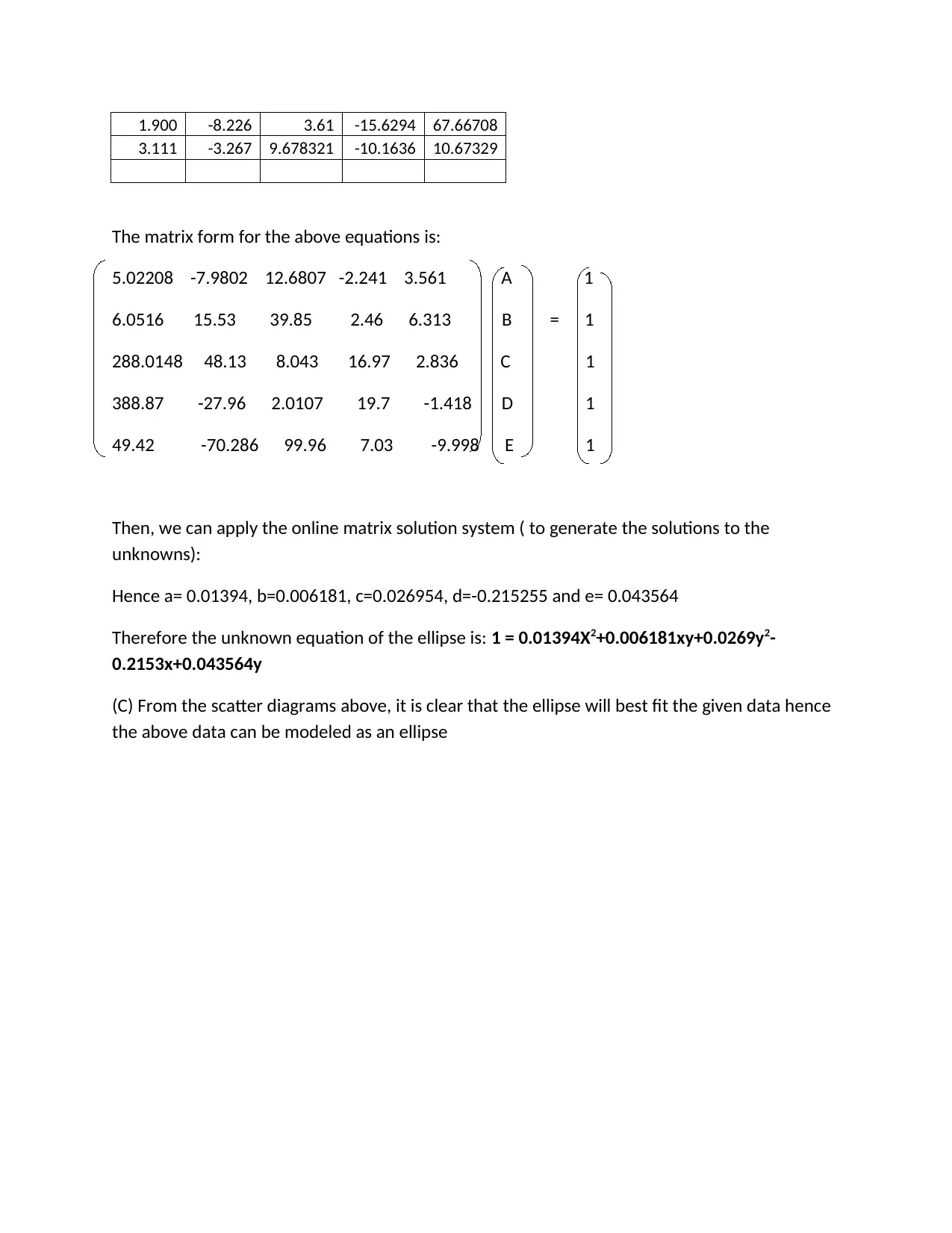
1.900 -8.226 3.61 -15.6294 67.66708
3.111 -3.267 9.678321 -10.1636 10.67329
The matrix form for the above equations is:
5.02208 -7.9802 12.6807 -2.241 3.561 A 1
6.0516 15.53 39.85 2.46 6.313 B = 1
288.0148 48.13 8.043 16.97 2.836 C 1
388.87 -27.96 2.0107 19.7 -1.418 D 1
49.42 -70.286 99.96 7.03 -9.998 E 1
Then, we can apply the online matrix solution system ( to generate the solutions to the
unknowns):
Hence a= 0.01394, b=0.006181, c=0.026954, d=-0.215255 and e= 0.043564
Therefore the unknown equation of the ellipse is: 1 = 0.01394X2+0.006181xy+0.0269y2-
0.2153x+0.043564y
(C) From the scatter diagrams above, it is clear that the ellipse will best fit the given data hence
the above data can be modeled as an ellipse

-5.000 0.000 5.000 10.000 15.000 20.000 25.000
-12.000
-10.000
-8.000
-6.000
-4.000
-2.000
0.000
2.000
4.000
6.000
8.000
Y
Y