Medical Claim Analysis and Specialist Impact

This assignment involves analyzing medical claim data to investigate the relationship between specialist type, claim severity, and average claim amount. Students examine trends in claim representation by different specialists and analyze how specialist involvement influences claim severity and costs. The analysis includes comparisons between orthopedic surgeons and other specialists, exploring factors like average claim amounts for severe conditions.

Analysis of Claims

Table of Contents
INTRODUCTION...........................................................................................................................1
1...................................................................................................................................................1
2...................................................................................................................................................1
3.a ...............................................................................................................................................2
3.b................................................................................................................................................2
3.c ...............................................................................................................................................4
3. d ..............................................................................................................................................5
3.e................................................................................................................................................6
4.a ...............................................................................................................................................7
4.b................................................................................................................................................8
REFERENCES................................................................................................................................9

INTRODUCTION
Malpractices in medical has been increased as per the study published in US news and
World Report. The medical malpractice in United States accounts for $55.6 billion a year (Sachs,
2018). In accordance with this context, the report aid in examining the data collated by The
UnitedHealth Group of America, a health insurance provider. The aim is to develop a better
understanding of claim paid out for medical malpractice lawsuit. Preliminary analysis of the
collected data will be made in order to produce an effective report showing which hypothesis are
supported and which are rejected.
1
The total Claim payment amount was $14.7 million. The overall summary of the data is provided
below in the table:
Table 1: Overall summary of claims
Amount
Mean 73457.49
Standard Error 2275.36
Median 72571.3
Mode 5400
Standard Deviation 32178.49
Sample Variance 1035455635.00
Kurtosis 5.99
Skewness 1.15
Range 227177.8
Minimum 1547
Maximum 228724.8
Sum 14691498.71
Count 200
Confidence Level(95.0%) 4486.91
1

The mean amount of the claim was $73457.49. Standard Deviation was 32178.49. The maximum
amount of claim taken by the claimants was $228724 and minimum was $1547. The data was
collected from 200 claimants who have taken claims in order to get medical support. Skewness is
a measure of the symmetry in a distribution. The Skewness was 1.15 and Kurtosis value was
5.99.
2
a) The average age of claimants
Out of 200 claimants the average age of claimant identified was 44.5 years.
b) The proportion of claimants with “No Insurance”.
Table 2: The proportion of claimants with “No Insurance”.
Insurance
Medicare/Medicaid 20
No Insurance 18
Private 95
Unknown 60
Workers Compensation
7
Total Result 200
From the above table it can be understood that out of total claimants 18 claims were No
Insurance. Thus, overall proportion of the No Insurance was 9%.
3.a
An industry report suggest that the average amount of paid claims has dropped below $77500.
The evidence to support this argument is provided below:
Table 3: One sample Test
One-Sample Test
Test Value = 77500
t df Sig. (2-tailed) Mean Difference 95% Confidence
Interval of the
Difference
2

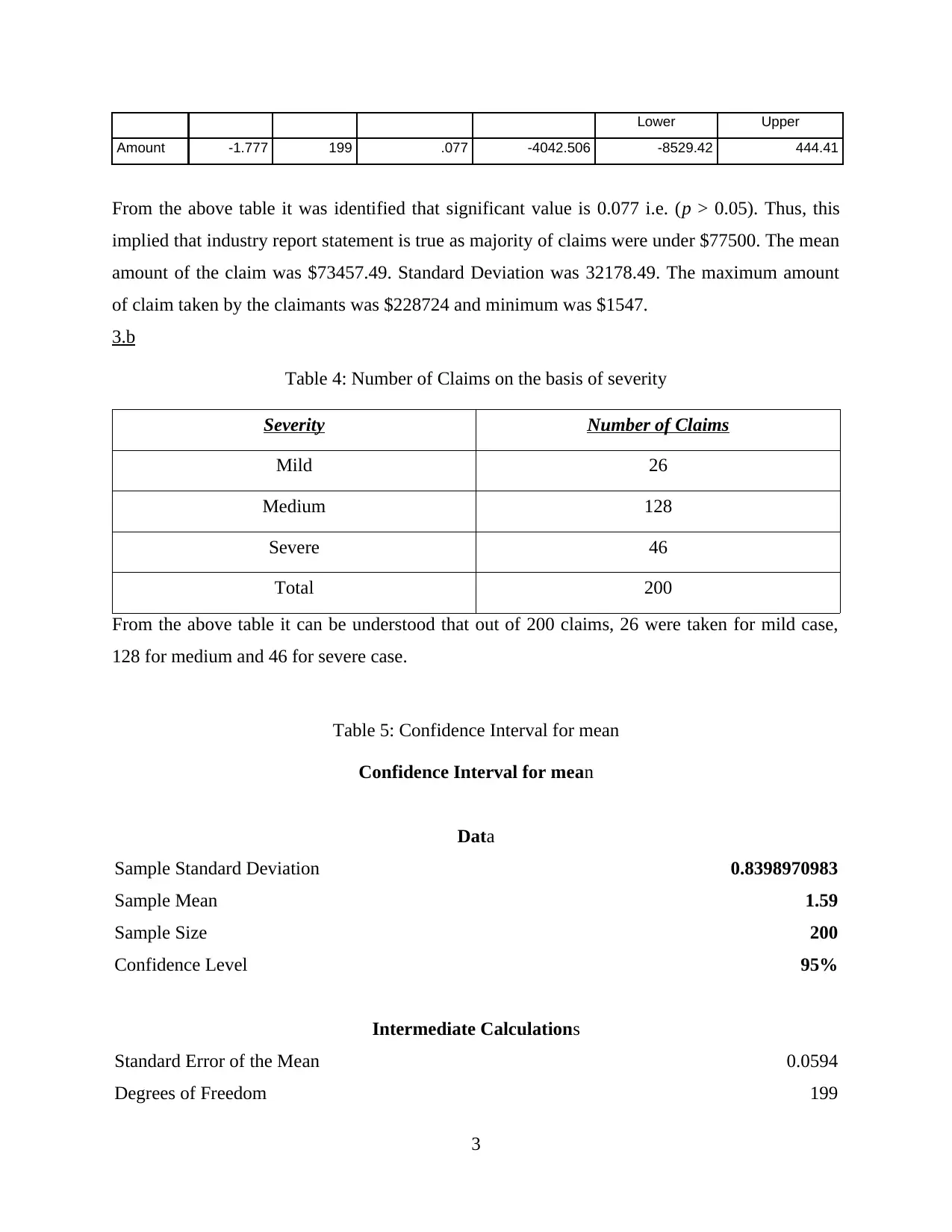
Lower Upper
Amount -1.777 199 .077 -4042.506 -8529.42 444.41
From the above table it was identified that significant value is 0.077 i.e. (p > 0.05). Thus, this
implied that industry report statement is true as majority of claims were under $77500. The mean
amount of the claim was $73457.49. Standard Deviation was 32178.49. The maximum amount
of claim taken by the claimants was $228724 and minimum was $1547.
3.b
Table 4: Number of Claims on the basis of severity
Severity Number of Claims
Mild 26
Medium 128
Severe 46
Total 200
From the above table it can be understood that out of 200 claims, 26 were taken for mild case,
128 for medium and 46 for severe case.
Table 5: Confidence Interval for mean
Confidence Interval for mean
Data
Sample Standard Deviation 0.8398970983
Sample Mean 1.59
Sample Size 200
Confidence Level 95%
Intermediate Calculations
Standard Error of the Mean 0.0594
Degrees of Freedom 199
3

t Value 1.9720
Margin of Error 0.1171
Confidence Interval
Interval Lower Limit 1.47
Interval Upper Limit 1.71
From the table it can be understood that sample mean value is 1.59 and t value is 1.9720. As the
t value is greater than significance value it can be concluded that null hypothesis is supported
which means that it is true that 3 out 4 claims were taken for mild or medium severity conditions.
Table 6: Confidence Interval for proportion
Confidence Interval for proportion
Data
Sample Size 200
Count of Successes 0.75
Confidence Level 95%
Intermediate Calculations
Sample Proportion 0.00375
Z Value 1.9600
Standard Error of the Proportion 0.0043220004
Margin of Error 0.0085
Confidence Interval
Interval Lower Limit -0.47%
Interval Upper Limit 1.22%
The count of success rate is 0.75 and z value is 1.96 which is greater than our significance value
(0.05). Thus, in this case null hypothesis is supported.
4

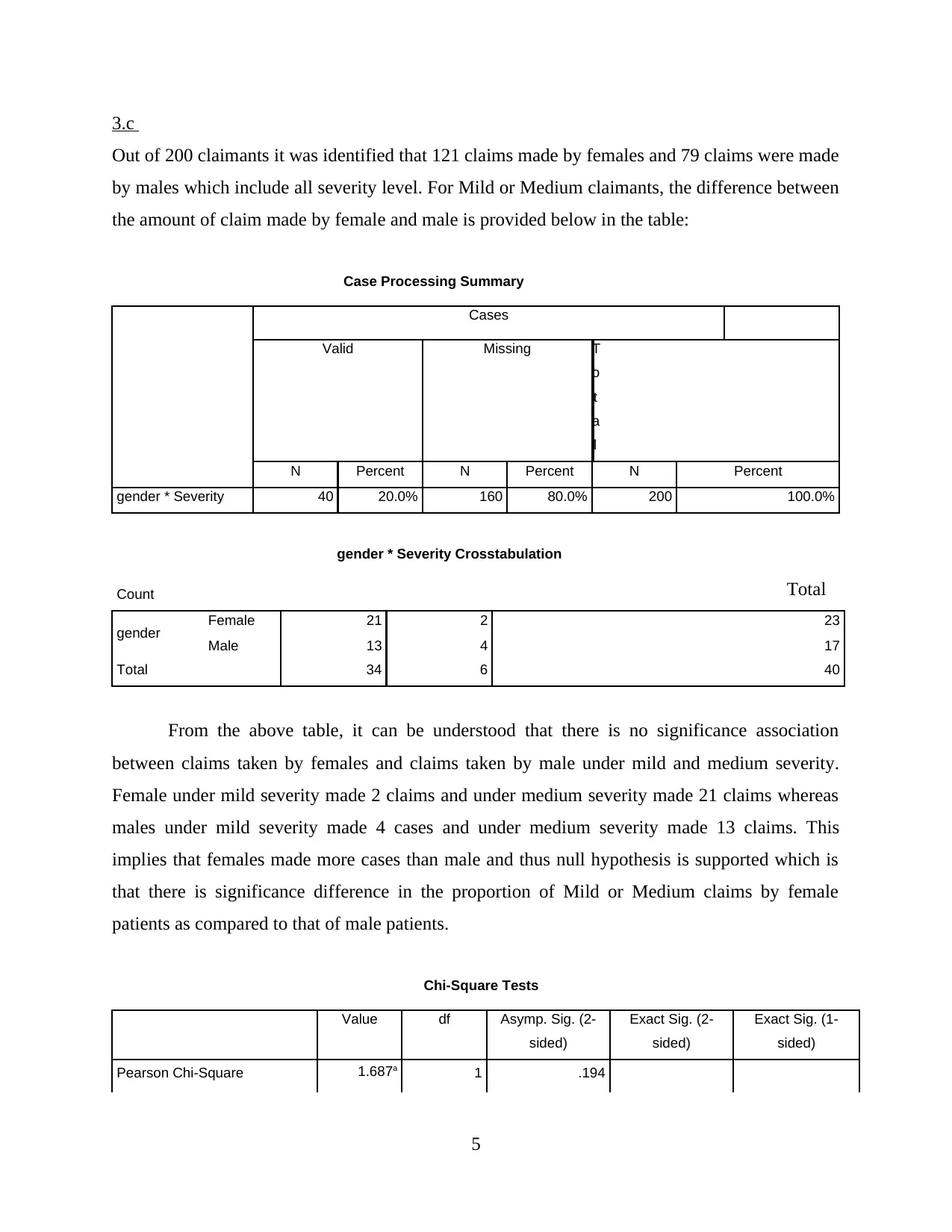
3.c
Out of 200 claimants it was identified that 121 claims made by females and 79 claims were made
by males which include all severity level. For Mild or Medium claimants, the difference between
the amount of claim made by female and male is provided below in the table:
Case Processing Summary
Cases
Valid Missing T
o
t
a
l
N Percent N Percent N Percent
gender * Severity 40 20.0% 160 80.0% 200 100.0%
gender * Severity Crosstabulation
Count Total
gender Female 21 2 23
Male 13 4 17
Total 34 6 40
From the above table, it can be understood that there is no significance association
between claims taken by females and claims taken by male under mild and medium severity.
Female under mild severity made 2 claims and under medium severity made 21 claims whereas
males under mild severity made 4 cases and under medium severity made 13 claims. This
implies that females made more cases than male and thus null hypothesis is supported which is
that there is significance difference in the proportion of Mild or Medium claims by female
patients as compared to that of male patients.
Chi-Square Tests
Value df Asymp. Sig. (2-
sided)
Exact Sig. (2-
sided)
Exact Sig. (1-
sided)
Pearson Chi-Square 1.687a 1 .194
5

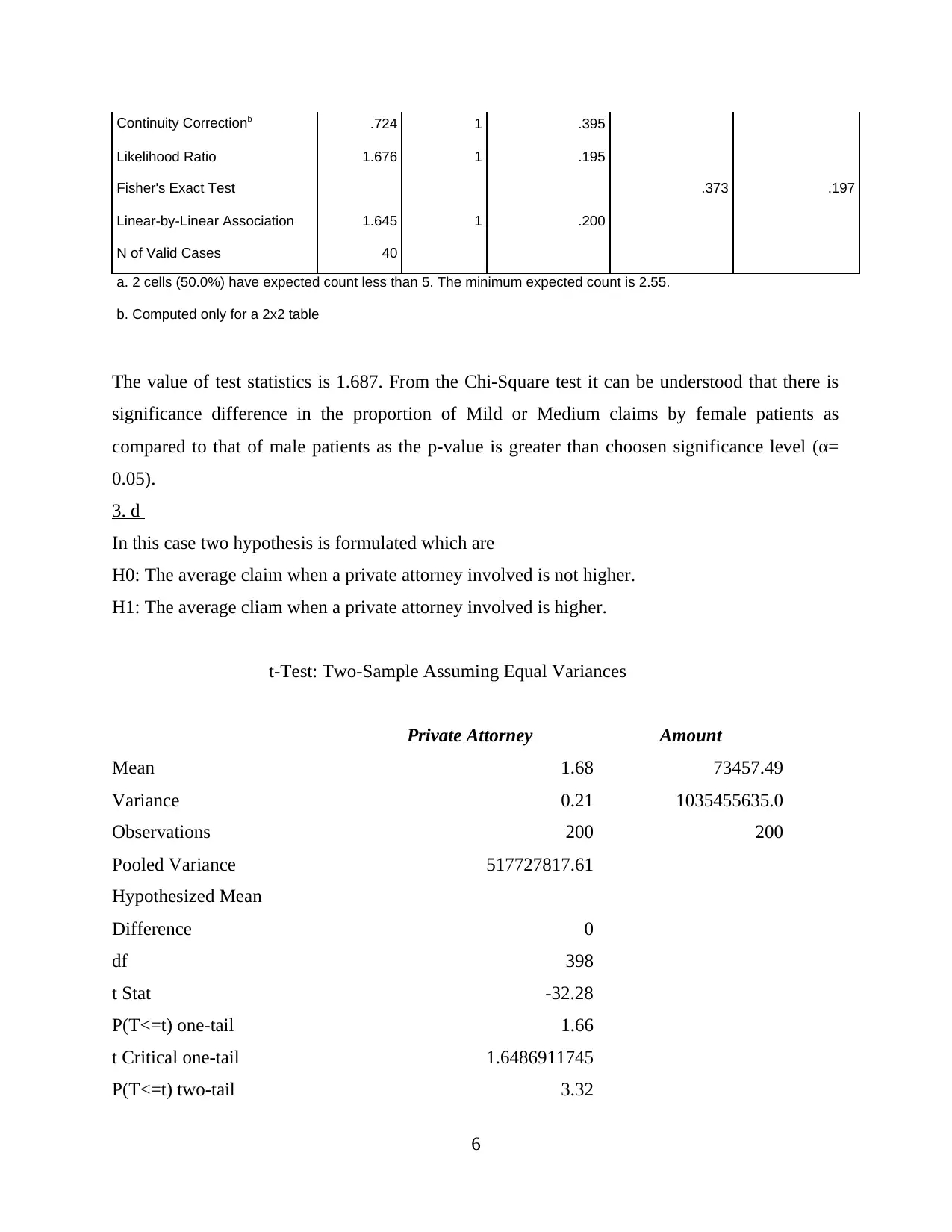
Continuity Correctionb .724 1 .395
Likelihood Ratio 1.676 1 .195
Fisher's Exact Test .373 .197
Linear-by-Linear Association 1.645 1 .200
N of Valid Cases 40
a. 2 cells (50.0%) have expected count less than 5. The minimum expected count is 2.55.
b. Computed only for a 2x2 table
The value of test statistics is 1.687. From the Chi-Square test it can be understood that there is
significance difference in the proportion of Mild or Medium claims by female patients as
compared to that of male patients as the p-value is greater than choosen significance level (α=
0.05).
3. d
In this case two hypothesis is formulated which are
H0: The average claim when a private attorney involved is not higher.
H1: The average cliam when a private attorney involved is higher.
t-Test: Two-Sample Assuming Equal Variances
Private Attorney Amount
Mean 1.68 73457.49
Variance 0.21 1035455635.0
Observations 200 200
Pooled Variance 517727817.61
Hypothesized Mean
Difference 0
df 398
t Stat -32.28
P(T<=t) one-tail 1.66
t Critical one-tail 1.6486911745
P(T<=t) two-tail 3.32
6

t Critical two-tail 1.96
The abvoe t test was Two-Sample Assuming Equal Variances. The p-value is 1.66 which is
greater than the significance value which (α= 0.05). Thus, it can be concluded that null
hypothesis is supported in this case.
t-Test: Two-Sample Assuming Unequal Variances
Private Attorney Amount
Mean 1.68 73457.49
Variance 0.21 1035455635.00
Observations 200 200
Hypothesized Mean
Difference 0
df 199
t Stat -32.28
P(T<=t) one-tail 2.43
t Critical one-tail 1.65
P(T<=t) two-tail 4.87
t Critical two-tail 1.97
The abvoe t test was Two-Sample Assuming Unequal Variances. The p-value is 2.43 which is
greater than the significance value which (α= 0.05). Thus, it can be concluded that null
hypothesis is supported in this case.
Thus, from both the table it can be understood that The average claim when a private attorney
involved is not higher. Hence, Null hupothesis which is H0 is supported in this case.
3.e
In this case two hypothesis is formulating which are :
H1: Private Attorney representation is higher for Severe Claims.
H2: Private Attorney representation is higher for Medium Claims
7

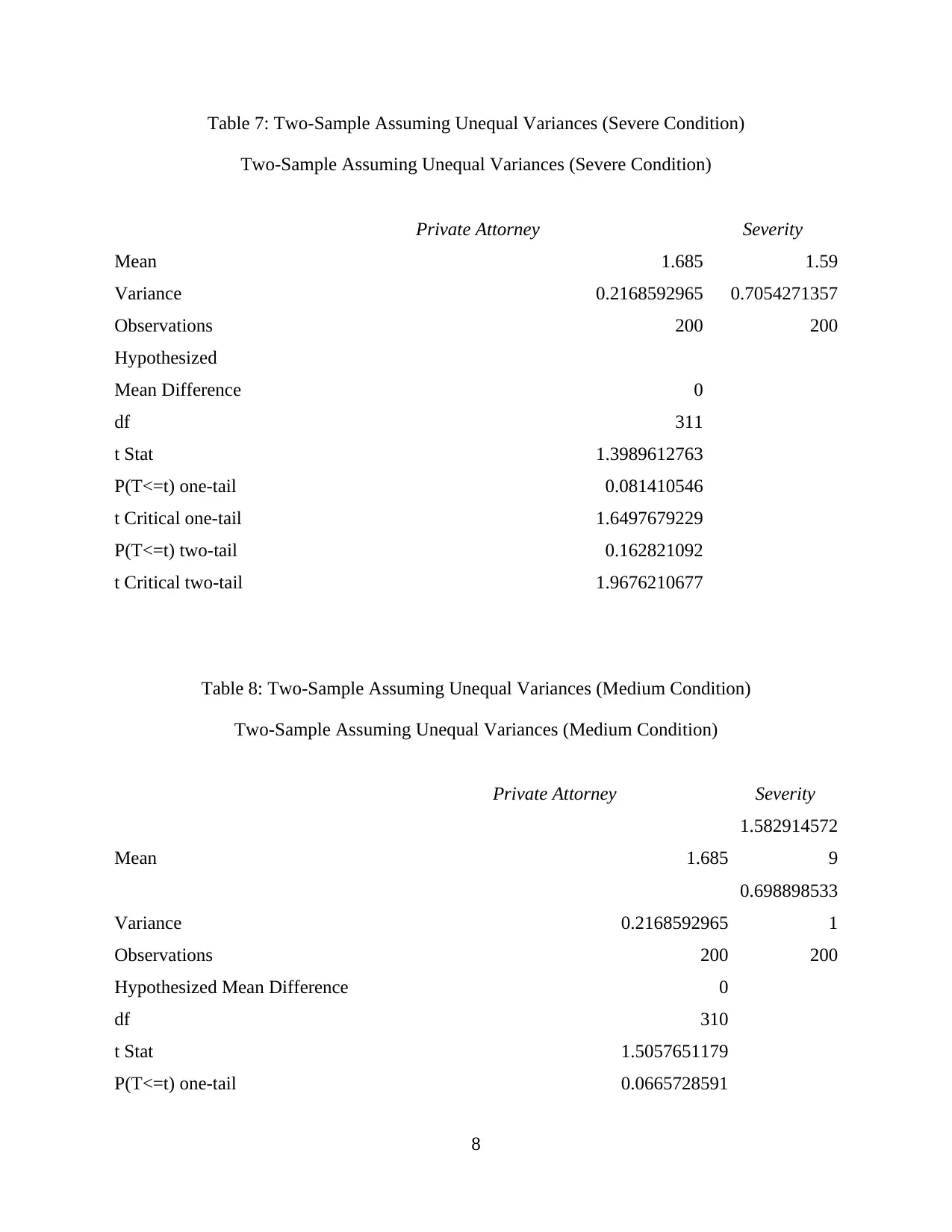
Table 7: Two-Sample Assuming Unequal Variances (Severe Condition)
Two-Sample Assuming Unequal Variances (Severe Condition)
Private Attorney Severity
Mean 1.685 1.59
Variance 0.2168592965 0.7054271357
Observations 200 200
Hypothesized
Mean Difference 0
df 311
t Stat 1.3989612763
P(T<=t) one-tail 0.081410546
t Critical one-tail 1.6497679229
P(T<=t) two-tail 0.162821092
t Critical two-tail 1.9676210677
Table 8: Two-Sample Assuming Unequal Variances (Medium Condition)
Two-Sample Assuming Unequal Variances (Medium Condition)
Private Attorney Severity
Mean 1.685
1.582914572
9
Variance 0.2168592965
0.698898533
1
Observations 200 200
Hypothesized Mean Difference 0
df 310
t Stat 1.5057651179
P(T<=t) one-tail 0.0665728591
8

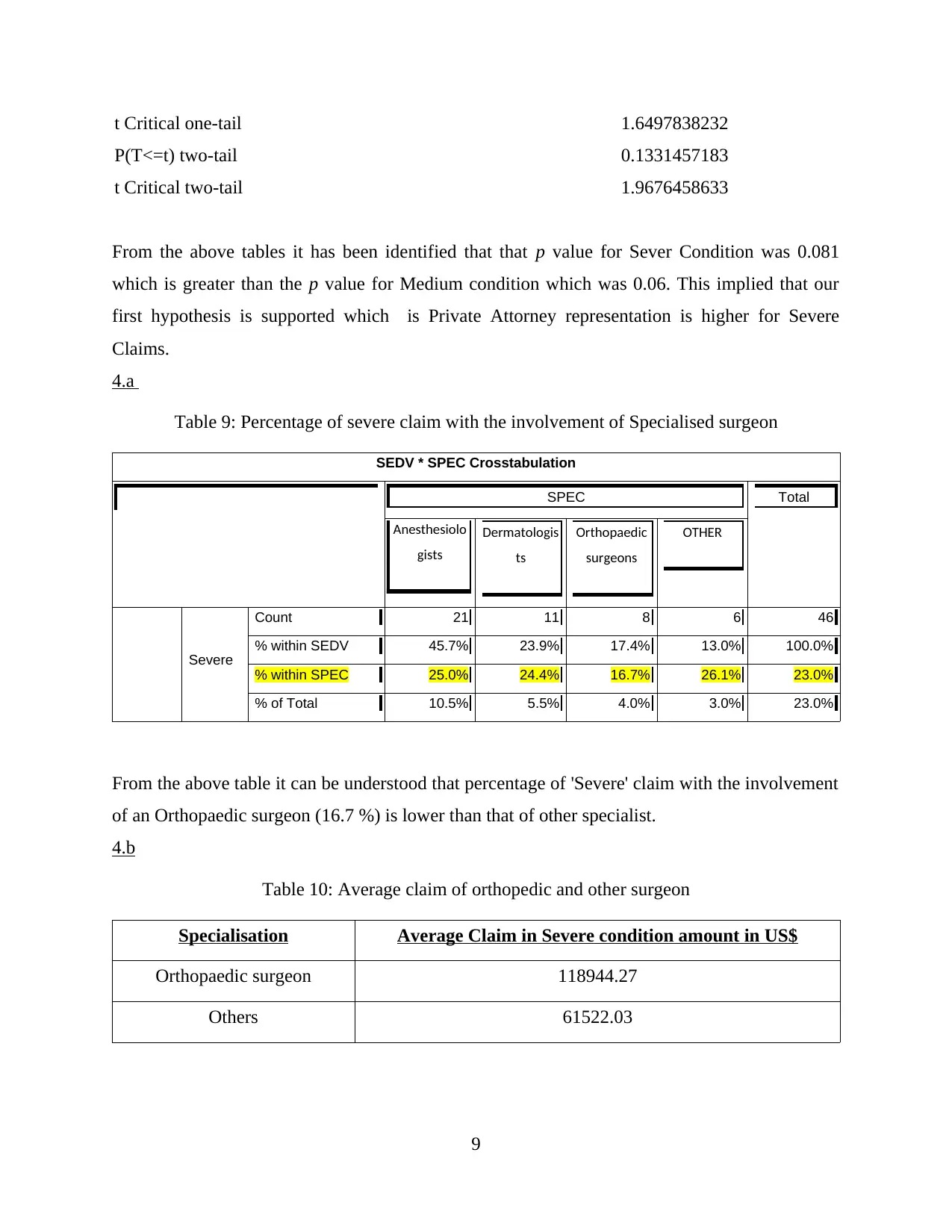
t Critical one-tail 1.6497838232
P(T<=t) two-tail 0.1331457183
t Critical two-tail 1.9676458633
From the above tables it has been identified that that p value for Sever Condition was 0.081
which is greater than the p value for Medium condition which was 0.06. This implied that our
first hypothesis is supported which is Private Attorney representation is higher for Severe
Claims.
4.a
Table 9: Percentage of severe claim with the involvement of Specialised surgeon
SEDV * SPEC Crosstabulation
SPEC Total
Anesthesiolo
gists
Dermatologis
ts
Orthopaedic
surgeons
OTHER
Severe
Count 21 11 8 6 46
% within SEDV 45.7% 23.9% 17.4% 13.0% 100.0%
% within SPEC 25.0% 24.4% 16.7% 26.1% 23.0%
% of Total 10.5% 5.5% 4.0% 3.0% 23.0%
From the above table it can be understood that percentage of 'Severe' claim with the involvement
of an Orthopaedic surgeon (16.7 %) is lower than that of other specialist.
4.b
Table 10: Average claim of orthopedic and other surgeon
Specialisation Average Claim in Severe condition amount in US$
Orthopaedic surgeon 118944.27
Others 61522.03
9