Analytical Method for Regression Analysis

This article discusses the analytical method for regression analysis with solved examples. It covers the significance of variables and how to conduct t-tests and F-tests. The article also includes a references list.

Running Head: ANALYTICAL METHOD
Analytical Method
Name of the Student
Name of the University
Author note
Course ID

1ANALYTICAL METHOD
Table of Contents
Answer v..........................................................................................................................................2
Answer vi.........................................................................................................................................3
Answer vii........................................................................................................................................3
Answer viii.......................................................................................................................................6
Answer ix.........................................................................................................................................7
References list..................................................................................................................................9

2ANALYTICAL METHOD
Answer v
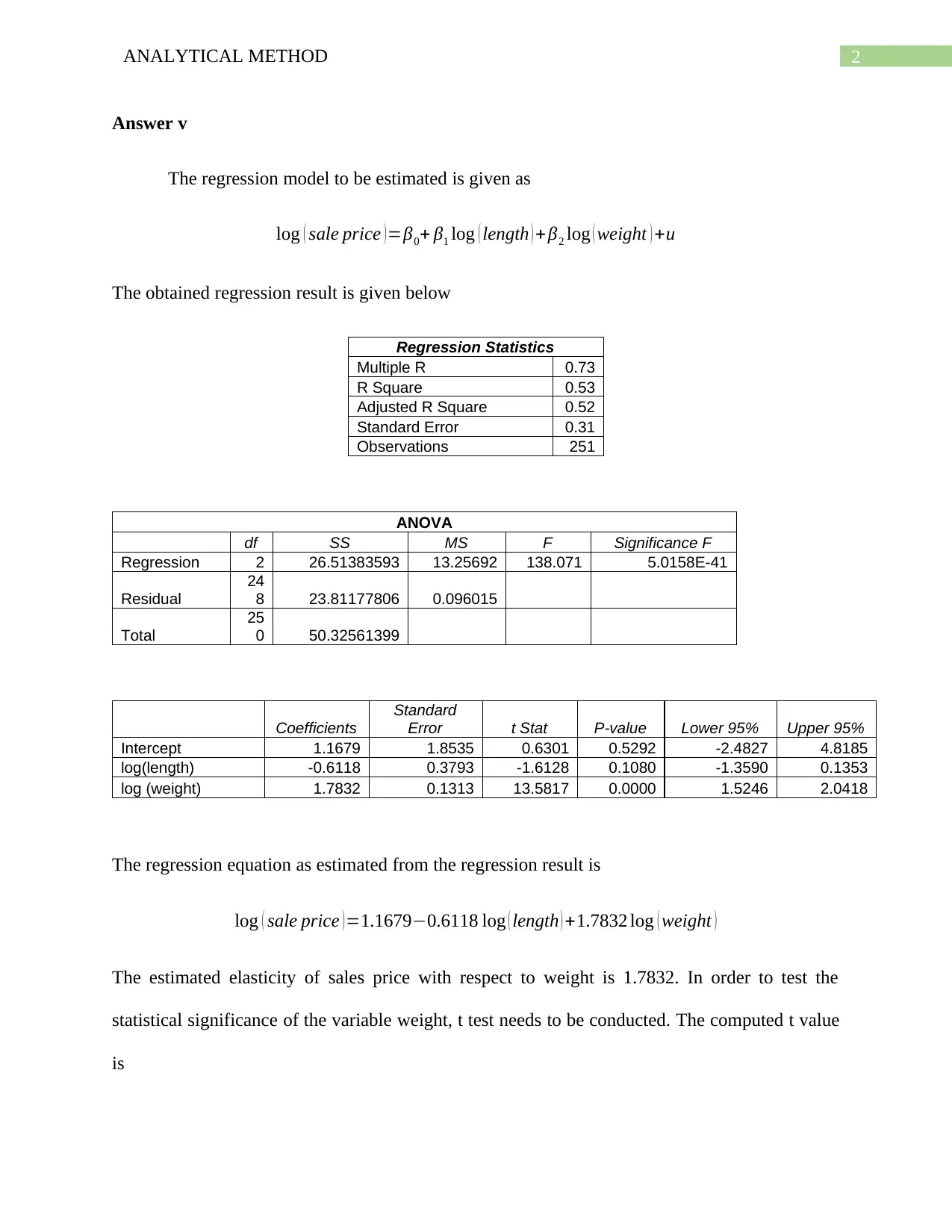
The regression model to be estimated is given as
log ( sale price )=β0+ β1 log ( length ) +β2 log ( weight ) +u
The obtained regression result is given below
Regression Statistics
Multiple R 0.73
R Square 0.53
Adjusted R Square 0.52
Standard Error 0.31
Observations 251
ANOVA
df SS MS F Significance F
Regression 2 26.51383593 13.25692 138.071 5.0158E-41
Residual
24
8 23.81177806 0.096015
Total
25
0 50.32561399
Coefficients
Standard
Error t Stat P-value Lower 95% Upper 95%
Intercept 1.1679 1.8535 0.6301 0.5292 -2.4827 4.8185
log(length) -0.6118 0.3793 -1.6128 0.1080 -1.3590 0.1353
log (weight) 1.7832 0.1313 13.5817 0.0000 1.5246 2.0418
The regression equation as estimated from the regression result is
log ( sale price )=1.1679−0.6118 log ( length ) +1.7832 log ( weight )
The estimated elasticity of sales price with respect to weight is 1.7832. In order to test the
statistical significance of the variable weight, t test needs to be conducted. The computed t value
is

3ANALYTICAL METHOD
t=
^β2
S . E of ¿ ¿
¿ 1.7832
0.1313
¿ 13.5817
The critical t value corresponding to 1% level of significance with 249 degrees of
freedom is 2.5957. As the computed t value is greater than the critical t value, it thus falls in the
critical or rejection region. The null hypothesis of no significant relation between weight and
sales price is thus rejected (Chatterjee and Hadi 2015). The variable thus is statistically
significant at 1% level. The result is further supported by the estimate of p value. The obtained p
value for the co-efficient is 0.0000. The p value less than the significance level again indicates
weight is statistically significant at the given level of significance.
Answer vi
The estimated coefficient for length is -0.6118. The negative value of the coefficient
indicates that length has a negative effect on the sales price. The computed t value is (-
0.6118/0.3793) = -1.6128. The critical t value at 1% level of significance and given degrees of
freedom is 2.5957. As the computed t value is less than critical t value, the null hypothesis of no
significant relation between length and sales price is accepted (Draper and Smith 2014). The p
value for the coefficient length equals 0.1080. As the p value is greater than significance level of
0.01, the variable length is statistically insignificant.
Answer vii
The regression model to be estimated is given as

4ANALYTICAL METHOD
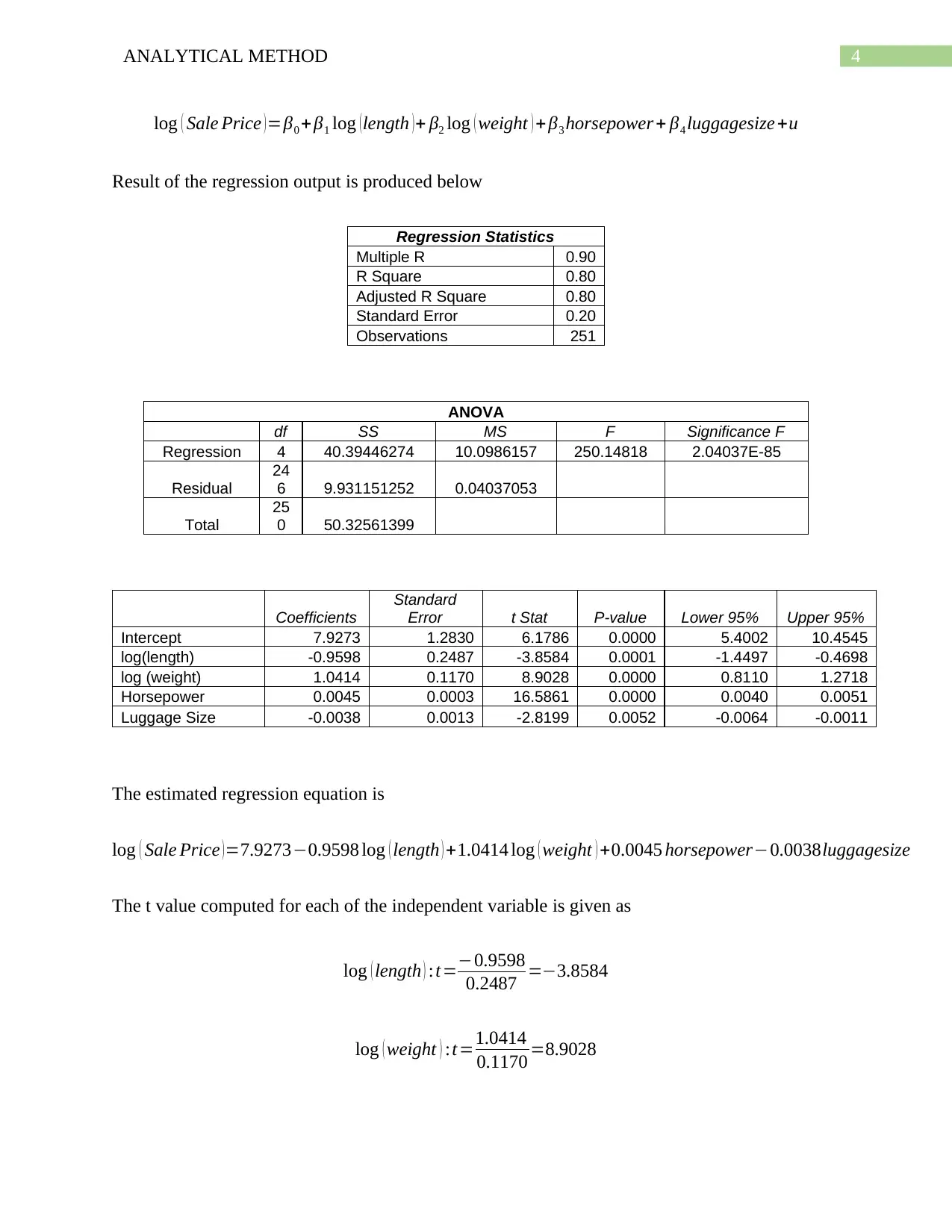
log ( Sale Price ) =β0 + β1 log ( length ) + β2 log ( weight ) + β3 horsepower + β4 luggagesize +u
Result of the regression output is produced below
Regression Statistics
Multiple R 0.90
R Square 0.80
Adjusted R Square 0.80
Standard Error 0.20
Observations 251
ANOVA
df SS MS F Significance F
Regression 4 40.39446274 10.0986157 250.14818 2.04037E-85
Residual
24
6 9.931151252 0.04037053
Total
25
0 50.32561399
Coefficients
Standard
Error t Stat P-value Lower 95% Upper 95%
Intercept 7.9273 1.2830 6.1786 0.0000 5.4002 10.4545
log(length) -0.9598 0.2487 -3.8584 0.0001 -1.4497 -0.4698
log (weight) 1.0414 0.1170 8.9028 0.0000 0.8110 1.2718
Horsepower 0.0045 0.0003 16.5861 0.0000 0.0040 0.0051
Luggage Size -0.0038 0.0013 -2.8199 0.0052 -0.0064 -0.0011
The estimated regression equation is
log ( Sale Price )=7.9273−0.9598 log ( length ) +1.0414 log ( weight ) +0.0045 horsepower−0.0038luggagesize
The t value computed for each of the independent variable is given as
log ( length ) :t=−0.9598
0.2487 =−3.8584
log ( weight ) :t=1.0414
0.1170 =8.9028

5ANALYTICAL METHOD
Horsepower :t= 0.0045
0.0003 =16.5861
luggagesize :t=−0.0038
0.0013 =−2.8199
The computed t values for all the independent variables are lower than critical t value of
2.5957. This implies that the four independent variables are statistically significant. The
conclusion further gains support from the obtained P values of the coefficient estimates. The p
values are less than significant value of 0.01. This in turn means rejection of null hypothesis of
no significant relation between Sales Price and the chosen independent variables (Darlington and
Hayes 2016).
For testing overall significance of the model, F test has to be conducted.
Hypothesis
Null Hypothesis (H0): β1=β2=β3=β4 =0
Alternative Hypothesis (H1): At least one of the coefficient is not zero
Test Statistics
F=
RSS
K
SSE
[n− ( k +1 ) ]
= Meanregrssion∑ of square
Meansquared error = MSR
MSE F4,246
Using the regression result, the F value is computed as
F=
40.3945
4
9.9312
146

6ANALYTICAL METHOD
¿ 10.0986
0.0404
¿ 250.1481
Decision rule
The null hypothesis is rejected if the computed F value exceeds the tabulated F value at
the chosen level of significance (Wooldridge 2015).
Conclusion
At 5% significance level, the tabulated F value is 2.4083. As the tabulated F value is less
than computed F value the null hypothesis stating the model does not have statistical significance
is rejected. The model is therefore statistically significant as a whole. The corresponding p value
for the F statistics is 0.0000, which is less than 0.05. P value less than the significance level again
implies the model is overall significant.
Answer viii
The critical F value corresponding to 1% level of significance is obtained as 3.3962. The
computed F value exceeds the critical F value. This implies, the model has an overall
significance at 1% level of significance.

7ANALYTICAL METHOD
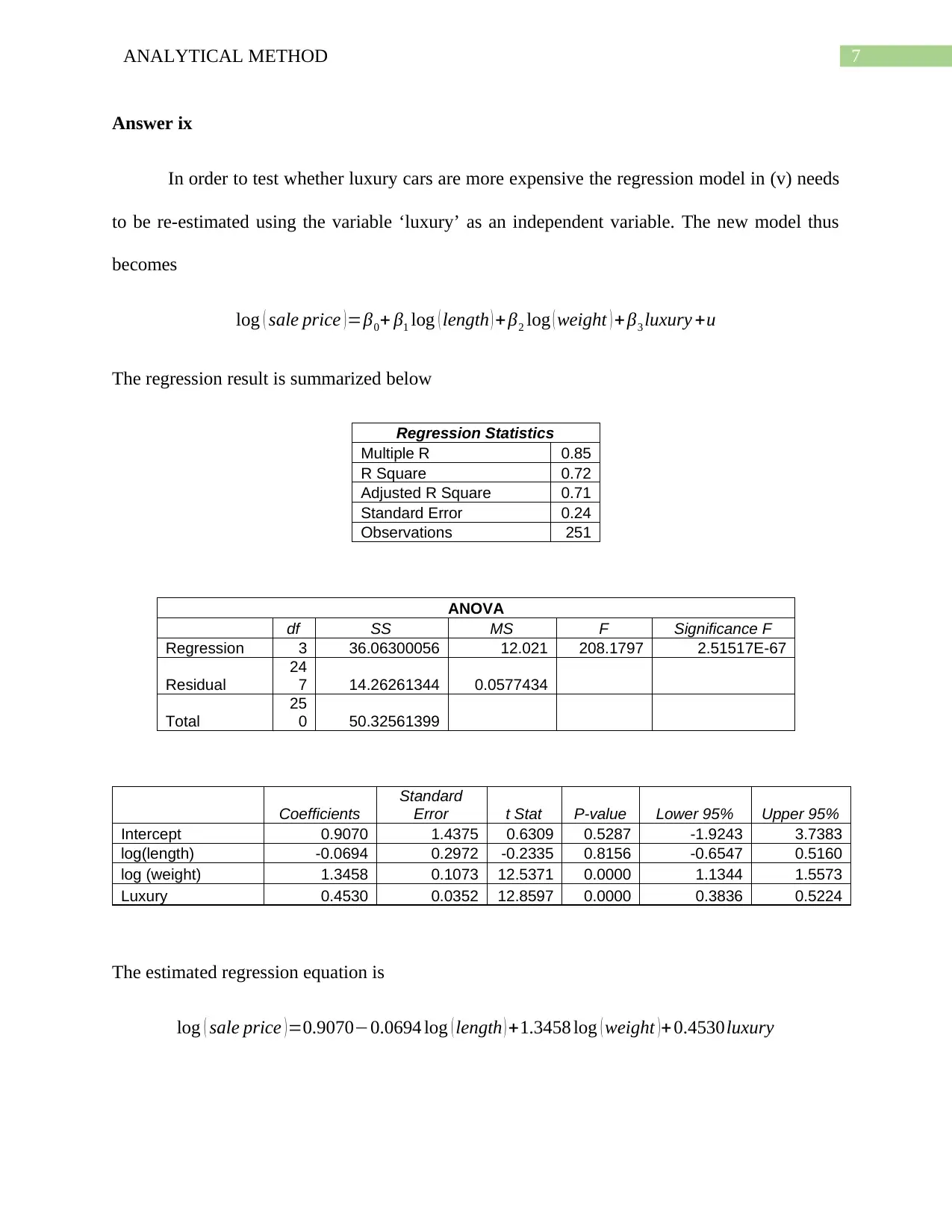
Answer ix
In order to test whether luxury cars are more expensive the regression model in (v) needs
to be re-estimated using the variable ‘luxury’ as an independent variable. The new model thus
becomes
log ( sale price ) =β0+ β1 log ( length ) + β2 log ( weight ) +β3 luxury +u
The regression result is summarized below
Regression Statistics
Multiple R 0.85
R Square 0.72
Adjusted R Square 0.71
Standard Error 0.24
Observations 251
ANOVA
df SS MS F Significance F
Regression 3 36.06300056 12.021 208.1797 2.51517E-67
Residual
24
7 14.26261344 0.0577434
Total
25
0 50.32561399
Coefficients
Standard
Error t Stat P-value Lower 95% Upper 95%
Intercept 0.9070 1.4375 0.6309 0.5287 -1.9243 3.7383
log(length) -0.0694 0.2972 -0.2335 0.8156 -0.6547 0.5160
log (weight) 1.3458 0.1073 12.5371 0.0000 1.1344 1.5573
Luxury 0.4530 0.0352 12.8597 0.0000 0.3836 0.5224
The estimated regression equation is
log ( sale price )=0.9070−0.0694 log ( length ) +1.3458 log ( weight )+ 0.4530luxury

8ANALYTICAL METHOD
The statistical significance of the variable luxury needs to be tested to decide whether
luxury cars are more expensive or not. The coefficient of luxury is positive having a value of
0.4530. The computed t statistics is (0.4530/0.0352) = 12.8597. The critical t value is 1.9697.
The computed t value exceeds the tabulated t value implying rejection of null hypothesis of no
significant relation between sales price and luxury. The associated p value for the coefficient is
0.0000. The p value lower than the significance level implies that the variable is statistically
significant at 5% level of significance. It can therefore be concluded that luxury cars are more
expensive relative to other types of cars.

9ANALYTICAL METHOD
References list
Chatterjee, S. and Hadi, A.S., 2015. Regression analysis by example. John Wiley & Sons.
Darlington, R.B. and Hayes, A.F., 2016. Regression analysis and linear models: Concepts,
applications, and implementation. Guilford Publications.
Draper, N.R. and Smith, H., 2014. Applied regression analysis(Vol. 326). John Wiley & Sons.
Wooldridge, J.M., 2015. Introductory econometrics: A modern approach. Nelson Education.