Comprehensive Solution: ANOVA, Regression Analysis Homework
VerifiedAdded on 2024/06/03
|4
|684
|367
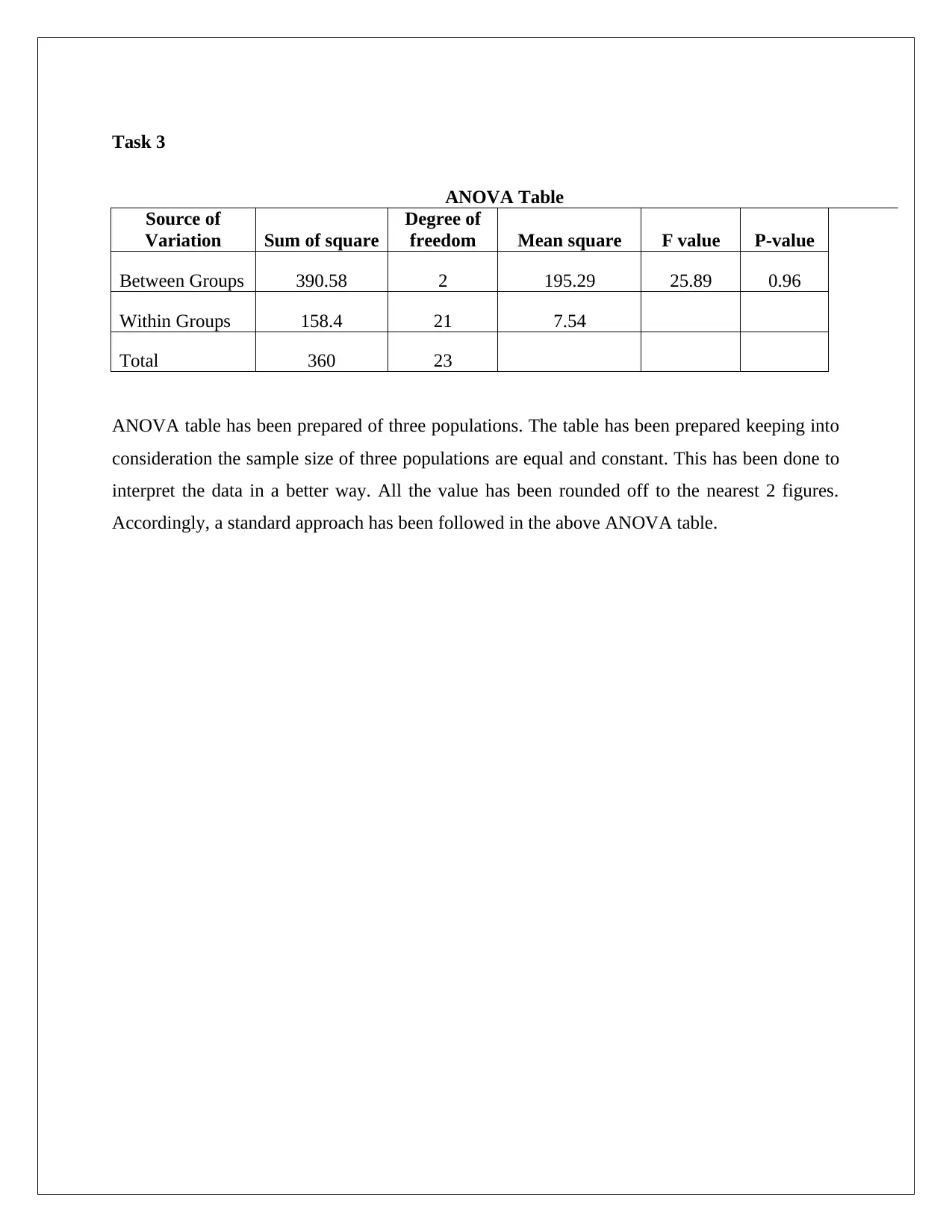
Homework Assignment
AI Summary
This assignment solution focuses on ANOVA and regression analysis, covering topics such as F-value interpretation, coefficient of determination, and regression coefficients. It includes calculations and interpretations related to ANOVA tables, regression equations, and the relationship between variables. Specifically, it addresses tasks involving the computation and analysis of variance, correlation coefficients, and the impact of variables on sales revenue. The solution provides detailed explanations and calculations to help understand the underlying statistical concepts and their practical applications in business scenarios. Desklib offers a wide range of similar solved assignments and study resources for students.
1 out of 4