Answer to Assignment 2

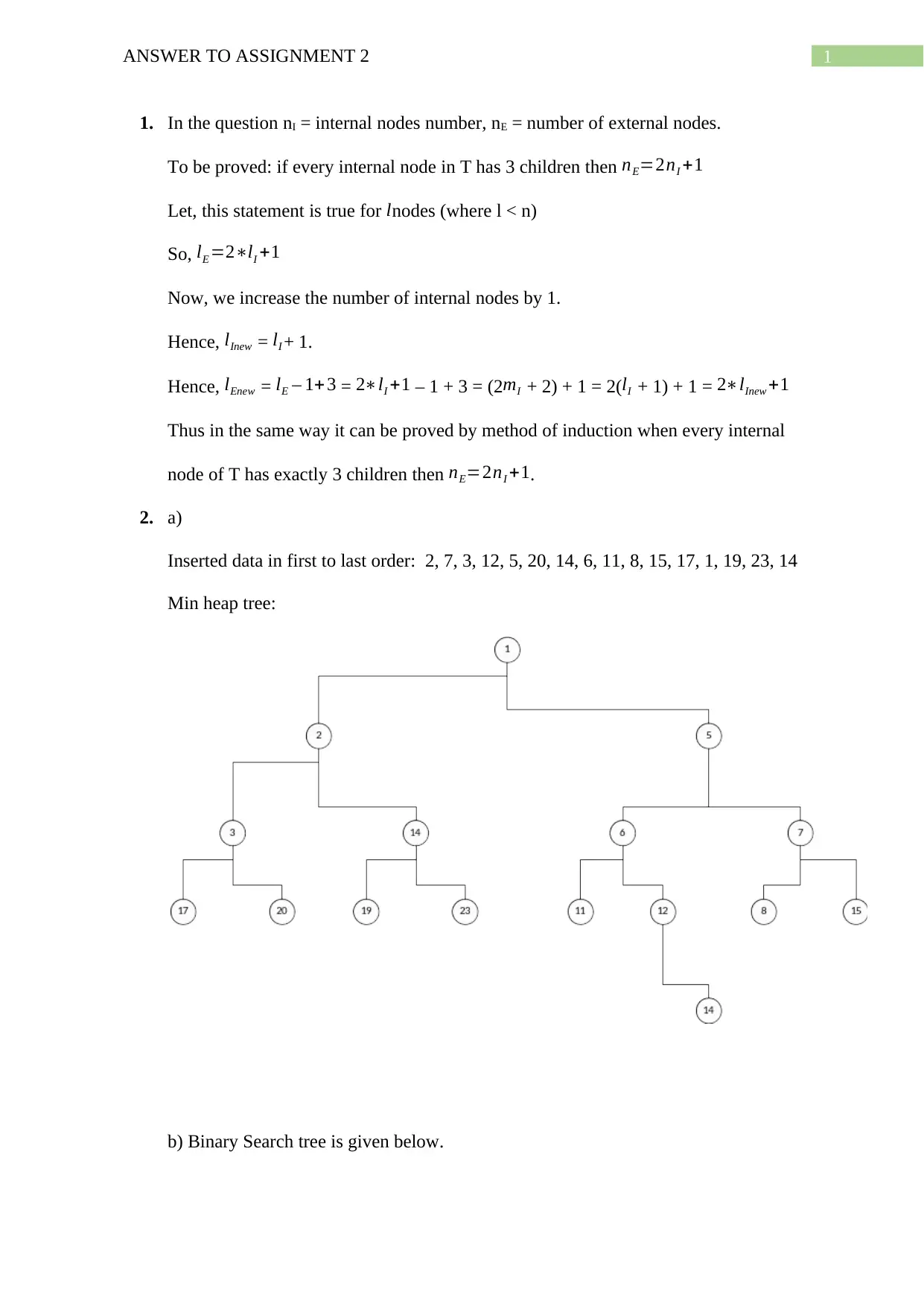
Get the answer to Assignment 2 with solved solutions and explanations. Find solutions for various topics including internal nodes, min heap tree, AVL tree, insertion sort, master theorem, and more.

Running head: ANSWER TO ASSIGNMENT 2
ANSWER TO ASSIGNMENT 2
Name of the Student
Name of the University
Author Note

1ANSWER TO ASSIGNMENT 2
1. In the question nI = internal nodes number, nE = number of external nodes.
To be proved: if every internal node in T has 3 children then nE=2nI +1
Let, this statement is true for lnodes (where l < n)
So, lE =2∗lI +1
Now, we increase the number of internal nodes by 1.
Hence, lInew = lI + 1.
Hence, lEnew = lE – 1+ 3 = 2∗lI +1 – 1 + 3 = (2mI + 2) + 1 = 2(lI + 1) + 1 = 2∗lInew +1
Thus in the same way it can be proved by method of induction when every internal
node of T has exactly 3 children then nE=2nI +1.
2. a)
Inserted data in first to last order: 2, 7, 3, 12, 5, 20, 14, 6, 11, 8, 15, 17, 1, 19, 23, 14
Min heap tree:
b) Binary Search tree is given below.

2ANSWER TO ASSIGNMENT 2
c) AVL tree:

3ANSWER TO ASSIGNMENT 2
d) [2,4] tree:
3.
i) Here, it is given that the input size is k and the worst case time complexity of
insertion sort is O(k^2). Thus the running time can be expressed in quadratic form
ak^2 + bk + c. Hence, the worst case time which is required to sort n/k sublists each
of length k size for insertion sort algorithm is provided by the following equation.
T(k) = (n/k)*(ak^2 + bk + c) = ank + bn + cn/k
For very large n the k become sufficiently small in comparison to n and thus the
second and third term of the above expression can be ignored.
Hence, T(k) = O(nk).
ii) Given, n elements are divided in n/k sorted sublists every one having length k.
Now, in order to merge the sorted sublists, 2 sublists are required to be taken at a time
and then merging is continued. Hence, the total steps required to merge n/k sorted
sublists is log(n/k). In each case n elements are compared and thus the time
complexity of the overall process will be O(nlog(n/k)).
iii) In a modified algorithm if the asymptotic running time is exactly same as the
standard time complexity of the standard sort then the time complexity O(nk +
nlog(n/k)) needs to be equal to O(nlogn).
Now, for satisfying the above condition increase of k can’t be faster than the
asymptotic increase of log(n) as if increase of k becomes faster than log(n) then

4ANSWER TO ASSIGNMENT 2
because of having nk number of terms the algorithm time complexity will be poor
than worst case asymptotic time O(nlog(n)).
Now, if k = O(log(n)) then
O(nk + nlog(n/k)) = O(nk + nlog(n) – nlog(k)) = O(nlog(n) + nlog(n) – nlog(log(n)))
= O(2nlog(n) – nlog(log(n))) = O(nlog(n)) (as log(logn)) is significantly smaller than
log(n) for large n)
So, the best k value is O(log(n)).
4.
i) In general the master theorem is, if the recurrence relation is of form
T(n) = aT(n/b) + f(n)
Here,
a,b >=1 are positive constants and the function f(n) is asymptotically positive.
If f(n) = O (nlogb (a −e ) ) for some e > 0, then
T(n) = Θ ( nlogb a )
Now, the given recurrence relation is
T(n) = 3T(n/2) + n
a = 3, b = 2, e=1 and f(n) = n = nlog2 (3−1 )
Hence, T(n) = Θ ( nlog2 3 ) by Master theorem.
Hence, the tight asymptotic upper bound by Master theorem of the recurrence relation
is T(n) = Θ ( nlog2 3 ).
ii)
Recursive tree method:

5ANSWER TO ASSIGNMENT 2
At level 0 cost is n
Level 1 cost will be n/2 + n/2 + n/2 = 3n/2
Level 2 cost will be 9(n/4)
Let at x level the cost is 1.
Hence, by recursion T(n) = Θ ( nlog2 3 )
iii) In the similar way by substitution method it can be shown that for substitution
method the asymptotic bound is T(n) = Θ ( nlog2 3 )
Let, we guess the solution is Θ ( nlog2 3 ).
Now, it is needed to proved by mathematical induction that T(n) <= c*( nlog2 3)
Where, c is any positive constant.
T(n) = 3T(n/2) + n <= c(n/2)log(3)/log(2) + n <= c*n^(log(3)/log(2)) + n <= c*( nlog2 3).
5. Given text is ‘advancedalgorithmanalysis’. Now, for finding the ‘rithm’ pattern the
brute force algorithm is chosen to be employed.
Brute force algorithm:
Algorithm BruteForceMatch(T[0...n-1], P[0...m-1])

6ANSWER TO ASSIGNMENT 2
for i ← 0 to n-m do
j ← 0
while j < m and P[j] = T[i+j] do
j++
if j = m then return i
return -1