CP5602: Ant Colony Optimization (ACO) Algorithm Report

This report delves into the intricacies of Ant Colony Optimization (ACO), a metaheuristic approach inspired by the foraging behavior of ants. It begins with an abstract that introduces ACO as a solution for combinatorial optimization problems, emphasizing the significance of pheromone laying in the algorithm's function. The report then explores ACO's application in the Traveling Salesman Problem and protein folding, offering a comprehensive introduction to the subject. Furthermore, it presents ACO's application to the Resource-Constrained Project Scheduling Problem (RCPSP). The report also provides a historical context for ACO's development and discusses its applicability in solving technical problems by transforming optimization problems into graph-based pathfinding scenarios. The process involves artificial ants constructing solutions, guided by a stochastic and pheromone-biased approach. The report is structured to give insights into ACO algorithms, showcasing how ACO optimization is applied to technical problems. It covers ACO's application in discrete and continuous optimization, beam search, constraint programming, and multilevel frameworks. Finally, it presents a comprehensive discussion of the Ant Colony Optimization algorithm.

Running head: ANT COLONY OPTIMIZATION
ANT COLONY OPTIMIZATION
Name of the Student
Name of the University
Author Note

ANT COLONY OPTIMIZATION 1
Abstract:
The ant algorithms are the multi agent systems in that the behaviour of every agent is
known as artificial ant where the algorithms are inspired by the behaviour of real ants. The
ant colony optimization is a metaheuistic approach that is proposed recently, to solve the
combinatorial optimization problems that are not so easy to understand. The pheromone
laying is the most inspiring source of Ant colony algorithm. The main purpose of this paper is
to discuss the techniques of the ant colony by using traveling salesman and protein folding
behaviour as the quick introduction. This is an approach that is presented for the RCPSP
(Resource constrained project scheduling problem). Several kinds of new features, which are
interesting for the ant colony optimization, are evaluated and proposed in general. This paper
also give an idea about the history behind developing the idea of ant colony optimization. The
report provides a brief idea about the ACO algorithms and discusses how the ACO
optimization is applicable for solving the technical problems. For applying the ACO, the
optimization problem has been transformed in the problem to find the best path on the
weighted graph. The solutions are built by the artificial ants when they move on the graph.
The process of the solution construction is so stochastic as well as it is biased by pheromone
model.

2ANT COLONY OPTIMIZATION
Table of Contents
Introduction:...............................................................................................................................3
The approach of Ant colony optimization:................................................................................3
Ant colony optimization algorithm:...........................................................................................4
The ant colony optimization met heuristic:................................................................................5
Algorithm: The ant colony optimization:...................................................................................6
Ant colony optimization application in discrete optimization problems:..................................9
Application of ant colony optimization in continuous optimization:.......................................10
Ant Colony Optimization in beam search:...............................................................................11
Constraint programming and ant colony Optimization:...........................................................12
Ant colony optimization in a multilevel framework:...............................................................12
Ant colony optimization in auxiliary search space:.................................................................13
Conclusion:..............................................................................................................................14

3ANT COLONY OPTIMIZATION
Introduction:
Scientists and industrial technicians often use Optimization in solving technical
problems. Train scheduling, network design, shape optimization, and time table are some
examples of practical optimization challenges (Yagmahan, B. 2011). The traveling salesman
problem model was used by a salesman who needed to pass through all cities following the
shortest distance possible. The protein folding problem of lattice models and traveling
salesman problem are classes of optimization technique called combinatorial optimization
(Suarjaya, I. 2012). The combination optimization (CO) P=(S, f) is optimized to give a finite
set of S objects with the function f: S→R+ indicates positive value for the object s∈S. The
main objective is to find minimum value with integer, subset of item sets, permutations of
items and graphs as objects.
The Ant colony optimization approach is a modern technique for analyzing
approximation. Ant foraging characteristics inspire the technique of Ant Colony Optimization
(ACO) algorithm. Ant’s uses behavior communication in finding paths and food. This
technique is applied in ACO algorithms in a move of finding a solution such as in discrete
optimization problems. Algorithm approximation with ACO is analyzed by artificial
intelligence and is the most successful swarm intelligence strand. Data mining and clustering
technique is inspired by ants’ behavior for cemetery building and particles swarms’
optimization (Selvi & Umarani, 2010)
The approach of Ant colony optimization:
The idea was introduced in 1990’s by Marco Dorigo, ants behavior to govern its
territory to survive is an excellent example of the success of this technique. As the ants move
they leave pheromone trail on path. In finding an algorithm for discrete optimization, a
discretized and simplified model is elaborated. The model graph is represented by G= (V,E),

4ANT COLONY OPTIMIZATION
vs and vd represent net of ants and found source respectively. The parameter e1 and e2 are
assigned length l1 and l2 where l1>l2. According to Matsuura (2012), the artificial pheromone
is represented by value τi, thus the probability of choosing an ant is given by P1 = τi/(e1 +e2 ) ,
i = 1,2 the pheromone trails thickness shows the strength of trails τ i ←τi + Q /li , pheromone
evaporation artificial model is represented by τ i ← (1−ρ)•τi, where i =1,2, …. With ρ∈(0,1).
These illustrations of ants’ movement form the foundation of ant colony optimization as the
name suggests.
Ant colony optimization algorithm:
TSP model is mainly applied in simulation behavior of ants and cannot be applied to
CO problem directly, as pheromone value is associated directly to problem solutions. For the
model, the solutions of the problem considered are already known (Yong, W. 2015). The
unknown optimal solution is obtained through combination optimization. The solution
component should be moderate in size and finite.
Definition1. In TSP given an undirected graph with parameter G= (V, E), the variable
v represents cities while edge weights represent distance between the cities. The main
objective is to get short distance between the cities. Therefore, space S represent tours in G.

5ANT COLONY OPTIMIZATION
f(s) define the sum of edge-weights for an edge in s. TSP model is also used in solving
discrete optimization problem. Incase Xe = 1, then edge e will be among the toured cities. The
constructed TSP problem is made up of four cities, represented by four nodes. To get the
solution, the node for the ant is selected randomly (Aono et al., 2011). The current node is
marked dark gray while visited node is marked with light gray. Choices of ant marked with
dashed lines are done consistently. Probability of different options is given by underneath
graphic.
The ant colony optimization met heuristic:
The chart below shows how ant colony optimization works.
When a CO problem presents, the finite set C is derived. The model assembles
solution for the problem. After obtaining the set, the defined set is represented as T. The
model is derived from a technical perspective of the parameterized probabilistic model. It is
the central components for ant colony optimization model. The model above is used in
generating probabilistic solutions for the problem under consideration through assembling the
components. The ACO technique helps in solving problems using appropriate steps (Wong,
K. 2010). First, the pheromone model help in constructing candidate solutions, a

6ANT COLONY OPTIMIZATION
parameterized probability distribution for search space. Then the next step candidate modifies
pheromone values as measure of estimating bias in the sampling for high-quality solutions.
Solution components reinforcement depends on the quality of solution that is core to
ant colony optimization. The following algorithm expands more on ant colony optimization
techniques.
Algorithm: The ant colony optimization:
While termination conditions not met do
ScheduleActivities
AntBasedSolutionConstruction()
PheromoneUpdate()
endScheduleActivities
end while
The ACO run time is moderated by while loop principal. The algorithmic component
for iteration is gathered and constructed in ScheduleActivities which doesn’t specify the three
activities scheduled and synchronized, but the algorithm designer has to control the process
(Baterina & Oppus. 2010).
Algorithm2. Procedure AntBasedSolutionConstruction()
s= ()
Determine N(s)
While N(s)#∅do
c← ChooseFrom (N(s))

7ANT COLONY OPTIMIZATION
s← extend s through appending component c
Determine N(s)
end while
AntBasedSolutionConstruction(): finite set of solution is derived from the discrete
optimization under construction. The construction process begins with an empty sequence
represented as s = (), the sequence s is extended through addition of available component for
set represented by N (s
⊆C\s. The parameter N(s) depend on the solution constructed and
probabilistically step performed for respective pheromone model (Gupta & Thakkar. 2014).
The algorithms are defined by
p (ci |s)= {([τi]α •[η(ci)]β)/ (∑c j∈N(s) [τj]α •[η(cj)]β)}, ∀ci ∈N(s),
The variable η represent optional weight parameter which depends on current
sequence assign to heuristic value represented as η(cj) for the solution cj
∈N(s). heuristic
information is value given by weighting function. β and α values determine relationship
between heuristic information and pheromone information.
PheromoneUpdate(): ant colony optimization variant differ for pheromone values
applied. Pheromone evaporation is applicable in practice to prevent constant convergence of
algorithm for the sub-optimal section. The result of initial and earlier iterations increases
outcome of pheromone trail parameters (Yu, H. 2014).
τ i ←(1−ρ)•τi +ρ• ∑{s∈Supd|ci∈s} ws •F(s), where i =1, 2,...,n
The variable Supd represents solutions set used for the update, for ρ∈(0,1) represents
the evaporation rate, F :S→R+ demonstrates the quality function where f(s)<f(s’)
⇒
F(s)≥F(s’),
∀s≠ s’
∈ S. Supd comprise of solutions generated by respective iteration and

8ANT COLONY OPTIMIZATION
solution found at start of algorithm. The AS-update rule obtained from the above equation is
given by
Supd←Siter where ws =1 ∀s∈Supd,
Iteration-best uses the solutions generated by various respective iteration in the
pheromone values updating. Iteration-best is derived by the equation given below
S upd ← {sib=argmax(F(s)|s∈Siter)} where w(sib) =1,
The ACO algorithm applies variation for Iteration-best update rule mechanism which
avoids premature convergence in achieving excellent results.
DaemonActions(): the daemon action implements centralized actions performed by
single ant. One of daemon action application includes the collection of global data use when
deciding if it is essential or not in the search process to involve certain limits.
An ant colony optimization variant which is most successful is Max-MIN ant system
is abbreviated as MMAS. MMAS algorithms use τmin >0 as explicit lower bound for
pheromone value while F (sbs)/ ρ for upper bound (Ahmadizar, F. 2012). Ant colony system
differs from original AS algorithm as pseudo-random proportional perform probabilistic
construction procedure, ant colony system also uses BS-update rule when getting pheromone
trial parameters values and lastly pheromone update in finding corresponding solution
component. Hyper-Cube Framework is the recent development of the ant colony optimization
algorithm, which is characterized by pheromone update obtain from weight for solution
defined (Riadi, I. 2014).

9ANT COLONY OPTIMIZATION
Ant colony optimization application in discrete optimization problems:
The ant colony optimization can be derived by proof-of-concept mean. The method is
applied in a classical problem such as scheduling problems, maximizing clique problem,
assignment problems, and vehicle routing problems (Afshar, M. 2010). Also, the technique is
involved in the cell placement problem, communication network designs among other fields.
The technique is applied in protein folding in multiplying the sequence alignment and
predicts primary histocompatibility complex binders. It involves finding the functional shape
for protein in 3 or 2-dimensional spaces; an example of this method include a hydrophobic-
polar model that uses simplified lattice models (Fidanova, S. 2010). Multiple sequences
alignment involves alignment of DNA sequences to find similarity between them. According
Benyahia (2012), ant colony optimization algorithm entails stochastic search technique where
pheromone update is prevented reaching optimization. The convergence value represents
probability of generated algorithm to optimize result more than once. An example of
convergence proof includes graph-based a system (Askarzadeh, A. 2016).

10ANT COLONY OPTIMIZATION
Application of ant colony optimization in continuous optimization:
In optimizing problem decision variables consist of constant domains, which is central
to discrete domains for variables used in discrete optimization (Hong, W. 2010). Initially, the
ACO algorithm was introduced to solve discrete problems; its adoption brought many
attentions. The API algorithm and continuous interacting ant colony were early applications
of anti-based algorithm (Papliński, J. 2013). In discrete optimization, solutions constructed
from the sampling of discrete probability solution derived from pheromone information. But
for continuous optimization, the continuous probability density function is utilized. The
density function in each solution is constructed from population solution which algorithms
keep every time. Taking a population with k cardinality parameter for the algorithm then
filled it with a random solution; it corresponds with pheromone solution initialized in the
optimization process for discrete solution.
The ant colony optimization algorithm constructive nature makes it suitable to be
applied in hybridization. For tree search, solution construction mechanism algorithm maps
search tree with the root node to the corresponding node. Beam search, rollout and pilot
techniques, backtracking techniques, greedy algorithm, and constraint programming are some
of AI and OR techniques that involve ant colony optimization idea (Song, Y.2013).

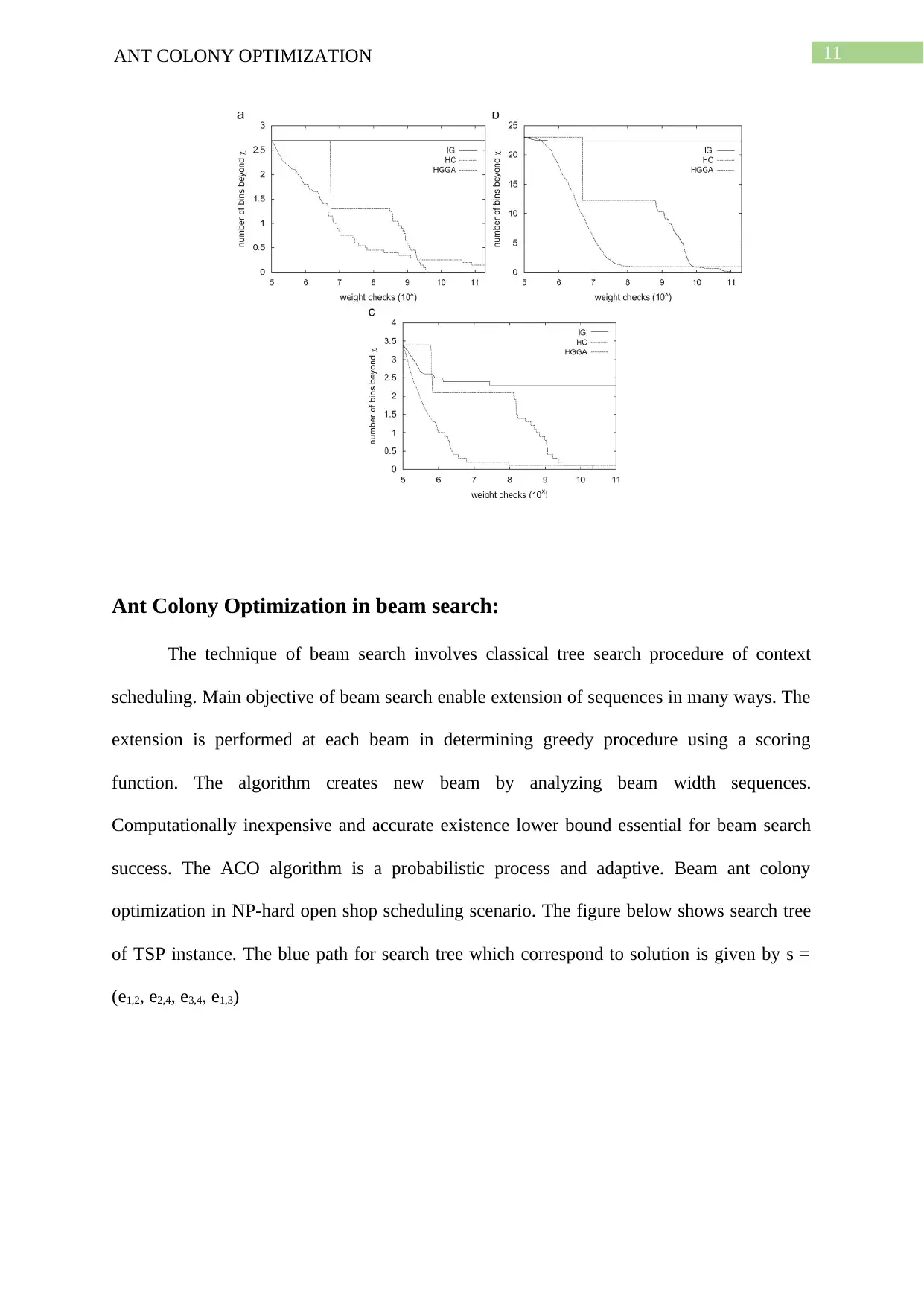
11ANT COLONY OPTIMIZATION
Ant Colony Optimization in beam search:
The technique of beam search involves classical tree search procedure of context
scheduling. Main objective of beam search enable extension of sequences in many ways. The
extension is performed at each beam in determining greedy procedure using a scoring
function. The algorithm creates new beam by analyzing beam width sequences.
Computationally inexpensive and accurate existence lower bound essential for beam search
success. The ACO algorithm is a probabilistic process and adaptive. Beam ant colony
optimization in NP-hard open shop scheduling scenario. The figure below shows search tree
of TSP instance. The blue path for search tree which correspond to solution is given by s =
(e1,2, e2,4, e3,4, e1,3)