Applied decision modeling.

Find here attached are assignments 1 & 2

Applied decision modeling
Name of the student
Name of the university

Project 1:
Let us consider, the Molokai Nut Company (MNC) needs to produce A pound of chocolate-
coated whole nuts (Whole), B pound of chocolate-coated nut clusters (Cluster), C pound of
chocolate-coated nut crunch bars (Crunch), and D pound of plain roasted nuts (Roasted).
Hence, the decision variables are A, B, C and D.
Let us further consider P is the Profit that will be earned by the Molokai Nut Company
(MNC) from this operation.
Hence, the objective variable is P.
Now the given table is showing revenue and cost of each category of nuts.
Per Pound Revenue and Costs
Whole Cluster Crunch Roasted
Selling Price $5.00 $4.00 $3.20 $4.50
Variable Cost $3.15 $2.60 $2.16 $3.10
Hence, the total profit will be:
P = A*(5-3.15) + B*(4-2.60) + C*(3.20-2.16) + D*(4.50-3.10)
= 1.85*A + 1.40*B + 1.04*C + 1.40*D
Hence, the objective function will be
Max P = 1.85*A + 1.40*B + 1.04*C + 1.40*D
Now, the production unit has certain constraints as discussed below:
Constraint 1: Production Constraint
As per given information, below are the production constraints:
A >= 1000
400 <= B <= 500

C <= 150
D <= 200
Constraint 2: Machine hour Constraint
As per given information, each machine has maximum of 60 hours, that is, 3600 minutes’
time available. In addition, the following table is showing required time, for producing per
pound of each category products:
Minutes Required per Pound
Machine Whole Cluster Crunch Roasted
Hulling 1.00 1.00 1.00 1.00
Roasting 2.00 1.50 1.00 1.75
Coating 1.00 0.70 0.20 0.00
Packaging 2.50 1.60 1.25 1.00
Hence, the machine hour constraints will look like:
1*A + 1*B + 1*C + 1*D <= 3600
2*A + 1.5*B + 1*C + 1.75*D <= 3600
1*A + 0.70*B + 0.20*C + 0*D <= 3600
2.50*A + 1.60*B + 1.25*C + 1*D <= 3600
Constraint 3: Nuts and Chocolate Constraint
As per given information below are the nuts and chocolate constraints:
0.60*A + 0.40*B + 0.20*C + 1*D <= 1100
0.40*A + 0.60*B + 0.80*C + 0*D <= 800
Hence, the LP problem will look like:
Max P = 1.85*A + 1.40*B + 1.04*C + 1.40*D

Subject to,
A >= 1000
400 <= B <= 500
C <= 150
D <= 200
1*A + 1*B + 1*C + 1*D <= 3600
2*A + 1.5*B + 1*C + 1.75*D <= 3600
1*A + 0.70*B + 0.20*C + 0*D <= 3600
2.50*A + 1.60*B + 1.25*C + 1*D <= 3600
0.60*A + 0.40*B + 0.20*C + 1*D <= 1100
0.40*A + 0.60*B + 0.80*C + 0*D <= 800
A, B, C, D >= 0
Now, excel solver is used for solving this LP problem
The output is as mentioned below:

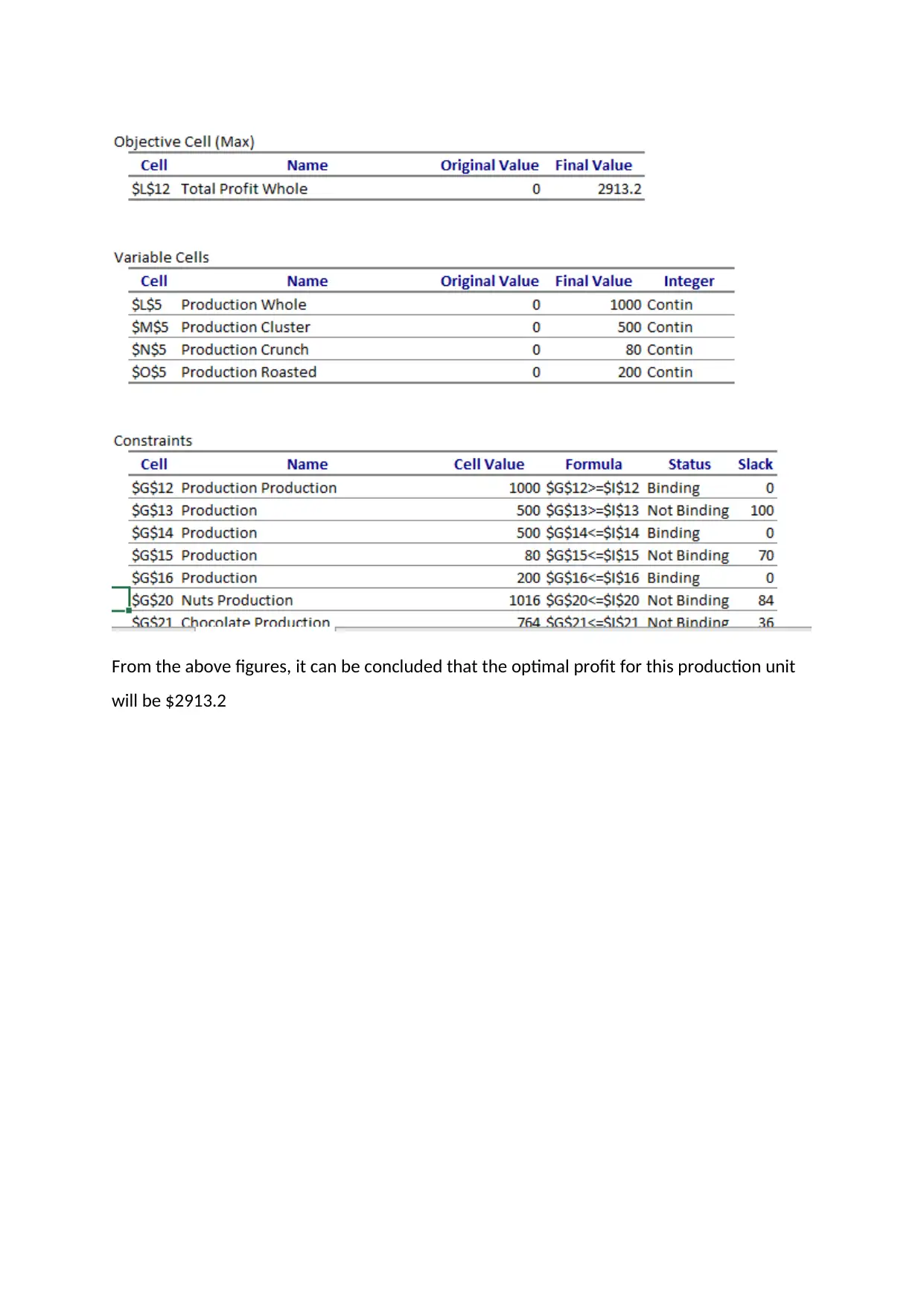
From the above figures, it can be concluded that the optimal profit for this production unit
will be $2913.2

Project 2:
The requirement was to minimize the cost of the Department of Transportation (DOT) is
planning to build a new interstate to run from Detroit, Michigan, to Charleston, South
Carolina.
The plan was given as mentioned below:
Let us consider, Xi denotes the routes from one node to another node, where i = 1,2,3,….,21
MS Excel has been used to design this optimal problem, where the aim was to minimize the
total cost. The excel model is shown as below:

From this model, it can be said that the total cost will be $8.00 to cover the route.