Applied Quantitative Methods Solutions

This document contains detailed solutions for problems related to statistics, probability, linear regression and more for the subject Applied Quantitative Methods. It includes tables, graphs and formulas for better understanding. The solutions are provided by an expert and can be accessed on Desklib along with other study material.

University
Applied Quantitative Methods
by
Your Name
Date
 <Your Name> 2018 1 of

Solutions
Question 1: Summary of Statistics and Graph
Problem Statement
Dataset for the prices of parts at each shelf in auto parts showroom in Melbourne is
provided. It is required that the frequency distribution using 10 classes, the frequency,
relative frequency and class midpoint is constructed. Additionally, a histogram is to be
constructed and the mean, mode and median be determined in excel.
Solution
A. The frequency distribution for the prices of parts is as shown below
Table 1: Frequency Distribution
B. The histogram for the above is created in excel and is as shown below:
Fig 1: Histogram
 <Your Name> 2018 2 of

C. The mean is given by the sum of the prices divided by the total number of prices
taken as shown below:
∑ x
x = 12602
60 =210.03
The mode is the most commonly appearing price and is 140.
The median is the price that appears at the middle and is
170+180
2 =175
Question 2: Measures of Variability and Association
Problem Statement
Dataset is provided to the manager of a baggage’s show room in the airport to discern
whether there is a relationship between the number of flights at the airport each day and
the number of baggage’s sold so that they can be kept in stock when the airport is busy over
the upcoming holiday.
Solution
a. The data set is a sample indicating the number of flights in the airport and the
baggage’s sold for seven weeks.
b. The standard deviation for the sample is given by;
σ = √ ∑ (x−μ)2
n−1
The values and computations need to be substituted above are as follows:
Table 2: Data for Standard Deviation
 <Your Name> 2018 3 of

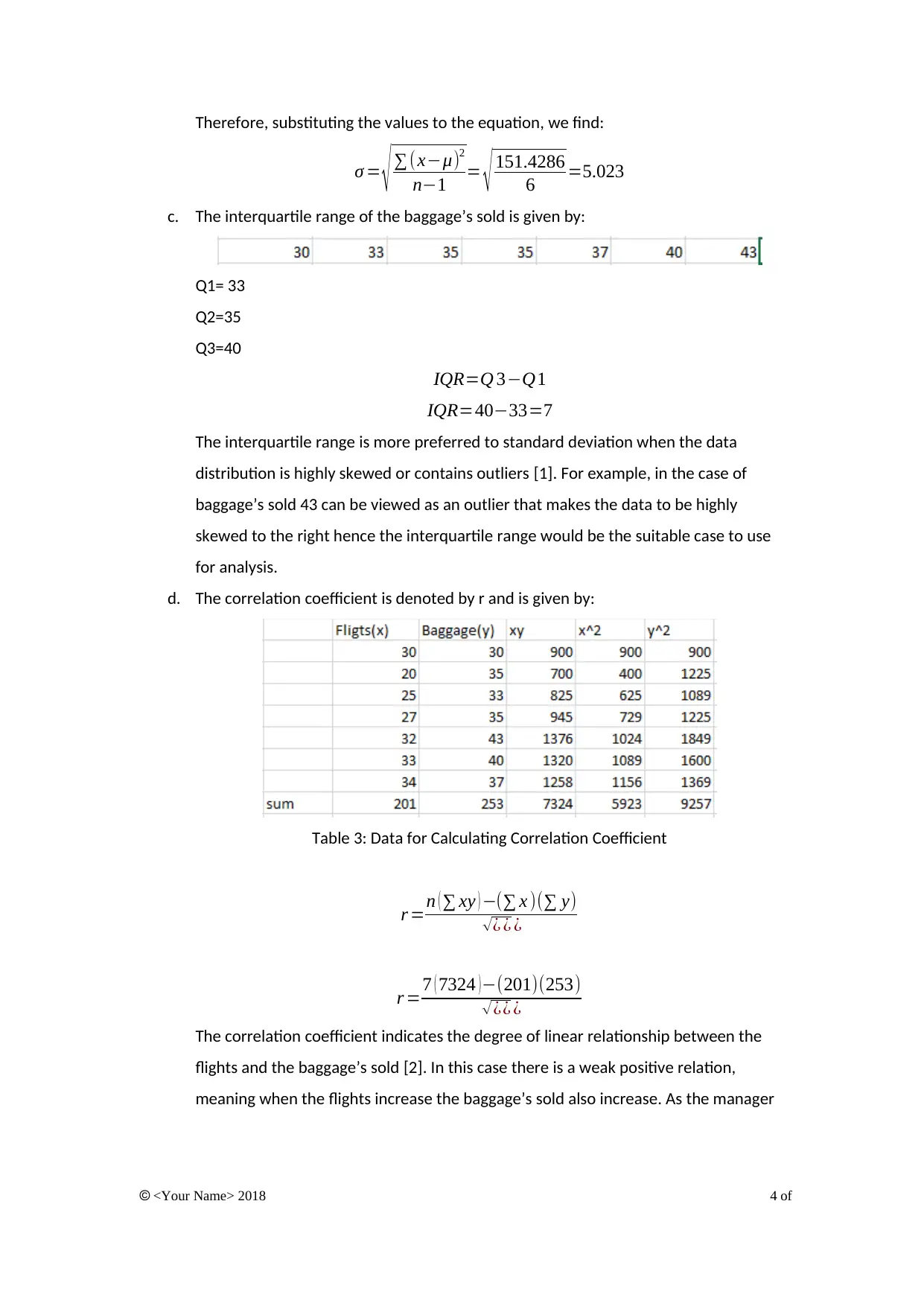
Therefore, substituting the values to the equation, we find:
σ = √ ∑ (x−μ)2
n−1 = √ 151.4286
6 =5.023
c. The interquartile range of the baggage’s sold is given by:
Q1= 33
Q2=35
Q3=40
IQR=Q 3−Q1
IQR=40−33=7
The interquartile range is more preferred to standard deviation when the data
distribution is highly skewed or contains outliers [1]. For example, in the case of
baggage’s sold 43 can be viewed as an outlier that makes the data to be highly
skewed to the right hence the interquartile range would be the suitable case to use
for analysis.
d. The correlation coefficient is denoted by r and is given by:
Table 3: Data for Calculating Correlation Coefficient
r =n ( ∑ xy ) −(∑ x )(∑ y)
√ ¿ ¿ ¿
r =7 ( 7324 )−(201)(253)
√¿¿ ¿
The correlation coefficient indicates the degree of linear relationship between the
flights and the baggage’s sold [2]. In this case there is a weak positive relation,
meaning when the flights increase the baggage’s sold also increase. As the manager
 <Your Name> 2018 4 of

of the showroom, the best thing to do would be to increase the baggage’s if the
flight increased and reduce them the flights reduced.
Question 3: Linear regression
Problem Statement
It is required of us to calculate the regression equation to determine the relationship
between the flights at the airport each day and the number of baggage’s sold.
Solution.
a. The regression equation of the form Y=mx+ c where y is the dependent variable,
x the independent variable, m is the slope and c is the intercept [3].
To calculate the slope, we use the formula below:
m= n ( ∑ xy ) −(∑ x)(∑ y )
n(∑ x2 )−¿ ¿
m= 7 ( 7324 ) −(201)(203)
7 ( 5923 )− ( 201 )2 = 405
1060 =0.39
The intercept is given by the formula below;
c= ( ∑ y ) ( ∑ x2 )−(∑ x) ( ∑ xy )
n(∑ x2)−¿ ¿
c= ( 253 ) ( 5923 )−201(7324)
7 ( 5923 ) − ( 201 )2 = 26395
1060 =24.9
The regression equation is thus y=0.39x+24.9 in our case y is the baggage
(Dependent variable) and x (independent) is the flights meaning that the baggage’s
sold is affected by the flights. For example, when there are 10 extra flights the
baggage’s sold is expected to increase by,
y=0.39 x +24.9=0.39 (10 )+ 24.9=28.8=29 baggage ' s .
b. The coefficient of determination is the square of the coefficient of correlation
expressed as a percentage
coefficient of determination R2=0.45352=0.2056
The value shows the possibility of future events falling within the predicted
outcome. Therefore, in our case if more samples are added for flights and
 <Your Name> 2018 5 of

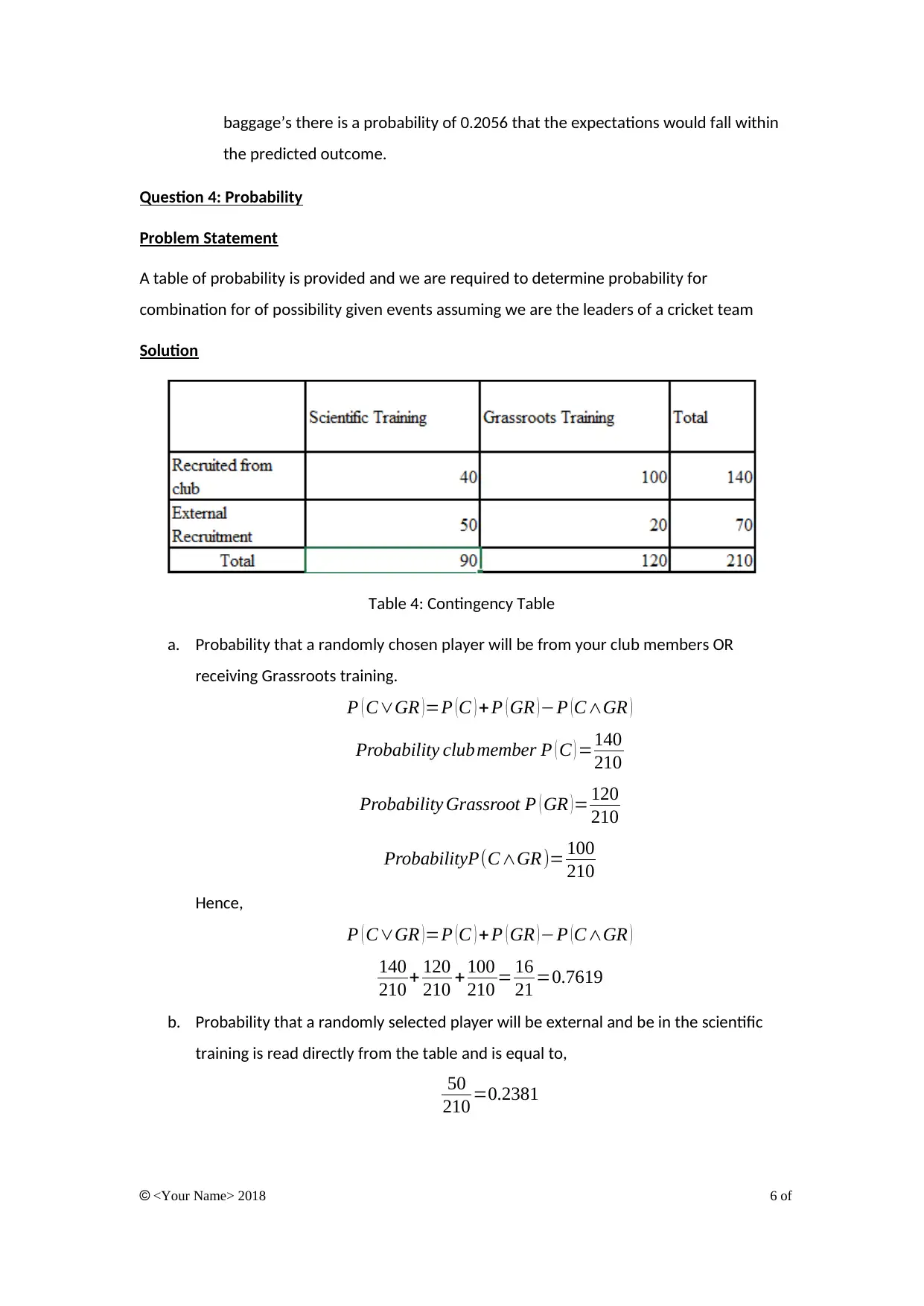
baggage’s there is a probability of 0.2056 that the expectations would fall within
the predicted outcome.
Question 4: Probability
Problem Statement
A table of probability is provided and we are required to determine probability for
combination for of possibility given events assuming we are the leaders of a cricket team
Solution
Table 4: Contingency Table
a. Probability that a randomly chosen player will be from your club members OR
receiving Grassroots training.
P ( C∨GR )=P (C ) +P ( GR )−P (C∧GR )
Probability clubmember P ( C ) =140
210
Probability Grassroot P ( GR ) = 120
210
ProbabilityP(C∧GR )= 100
210
Hence,
P ( C∨GR )=P (C ) +P ( GR )−P (C∧GR )
140
210 + 120
210 + 100
210 = 16
21 =0.7619
b. Probability that a randomly selected player will be external and be in the scientific
training is read directly from the table and is equal to,
50
210 =0.2381
 <Your Name> 2018 6 of

c. Probability that a player is in scientific training, given that player if from club
members.
P ( S|C ) = 40
140 =0.2857
d. Determination of whether training is independent from recruitment.
Here we need to show that,
P ( T ∧R ) =P ( T |R )∗P ( R ) =P ( T )∗P( R)
Using part B above for P (E and S), we have
P ( E∧S ) =P ( E |S )∗P ( S ) =P ( E ) XP( S)
P ( E∧S )= 50
210 =0.2381
P ( E ) =P ( External ) = 70
210
P ( S )=P ( Scientific Training ) = 90
210
P ( E|S )= 50
90
Now,
P ( E∧S ) =P ( E |S )∗P ( S ) =P ( E ) XP( S)
50
210 =
50
90∗90
210 = 70
210 X 90
210
0.238=0.238=0.761
Since they are not equal training is not independent from recruitment
Question 5: Bayes’ Rule
Problem Statement
Given the market consumer segments and their probability for preference of TV we are
required to offer advice to the electronic company on how probable that a consumer comes
from segment A and it is known that the consumer prefers TV over radio.
Solution
Probability of a consumer coming from segment A is,
 <Your Name> 2018 7 of

P ( SA )= 60
100 =0.6
The probability that a consumer from segment A having preference to TV is given by,
P ( TVA )= 30
100 =0.3
The probability of consumer coming from segment A and having a preference to TV is
therefore given by the following.
P=P ( SA ) XP ( TVA )
p=0.6 X 0.3=0.18
Question 6: Probability
Problem Statement
We are provided with the data for a festival that sells 2 million tickets for 2 dollars each and
the amount won for a ticket. We are required to calculate the mean and the standard
deviation of the amount won per ticket, interpret the mean and calculate the expected
profit form the festival.
Solution
Table 5: Data for Mean and Standard deviation
The mean is given by,
∑ x
x = 1000+100+20+10+4+ 2+1+ 0
8 =142.125
The mean of 142.124 represents the average amount won in the festival.
 <Your Name> 2018 8 of

The standard deviation is given by,
σ = √ ∑ (x−μ)2
n−1 = √ 848924.875
8 =328.07
The expected profit is calculated using the formula:
Expected profit probability=1−∑ ¿
Table 4: Probability and Price
Expected profit probability=1−0.67432=0.32568
The actual profit is given by the product of the profit probability and the actual
amount sold from the tickets as shown below:
Expected profit=0.32568 X 2 million X 2=1302720 dollars
Question 7: Probability
Problem Statement
We are provided with the speeds of train for which we are required to find the probability
given that the distribution of speed is normal with a mean of 250km/h and standard
deviation of 30km/hr.
Solutions
a. The probability that a train will average less than 200km/hr.
P(V<200km/hr.)
Z−score= Value−mean
stdev = 200−250
30 =−1.67
From the Z-table P(Z<-1.67) =0.0475.
b. The probability that a train will average more than 300km/hr.
 <Your Name> 2018 9 of

P(V>300km/hr.) is the same as 1- P(V>300km/hr.) hence,
Z−score for 300=Value−mean
stdev = 300−250
30 =1.67
From the Z-table P(Z<1.67) =0.9525. Thus,
P(V>300km/hr.) = 1-09525=0.0475
c. The probability that a train will average between 210 and 280km/hr.
P(210<V<280km/hr.)
Z−score for 210=Value−mean
stdev = 210−250
30 =−1.33
From the Z-table P(Z<-1.33) =0.0918.
Z−score for 280=Value−mean
stdev = 280−250
30 =1.00
From the Z-table P(Z<1.00) =0.8413.
P ( 210<V <280 ) =P ( V <280 )−P(V <210)
¿ 0.8413−0.0918=0.7495
Question 8: Probability
Problem Statement
We are required to calculate the probability that a random sample of 49 different one-hour
shopping periods yields a sample mean between 441 and 446 shoppers.
Solution
Mean number of shoppers =448 in one hour.
Standard deviation =21 shoppers
Sample size =49
The z score in this case will be given by the following formula:
Z−score= Value−mean
stdev
√ n
For a value of shoppers equals to 441, then
 <Your Name> 2018 10 of

Z−score= 441−448
21
√ 49
=−2.3
From the Z-table P(Z<-2.33) =0.0099
For a value of shoppers equals to 446, then
Z−score= 446−448
21
√49
=−0.67
From the Z-table P(Z<-0.67) =0.2514. Therefore,
P ( 241<V <446 )=P ( V < 446 )−P(V < 441)
0.2514−0.0099=0.2415
 <Your Name> 2018 11 of

References
[1] D. Rumsey, Intermediate Statistics for Dummies, Hoboken: Wiley, 2007.
[2] P. Bruce, Introductory Statistics and Analytics, New Jersey: Wiley, 2015.
[3] P. Newbold, W. Carlson and B. Thorne, Statistics for Business and Economics,
Harlow, Essex: Pearson Education, 2013.
 <Your Name> 2018 12 of