Trigonometry Assignment
VerifiedAdded on 2023/01/18
|8
|1042
|33
AI Summary
This assignment focuses on various topics in Trigonometry including polar expressions, rectangular coordinates, polar points, vector components, and more.
Contribute Materials
Your contribution can guide someone’s learning journey. Share your
documents today.
1 out of 8



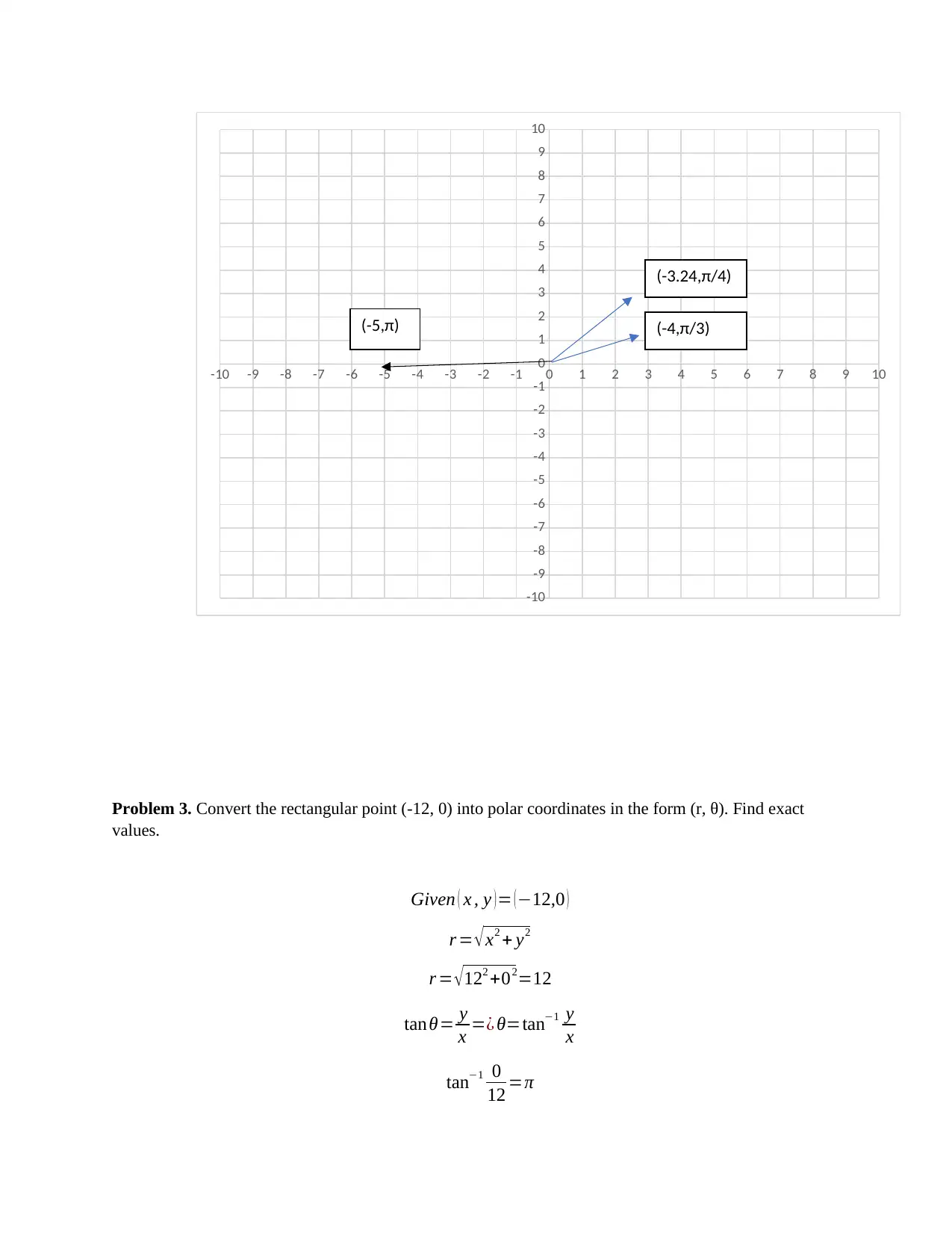
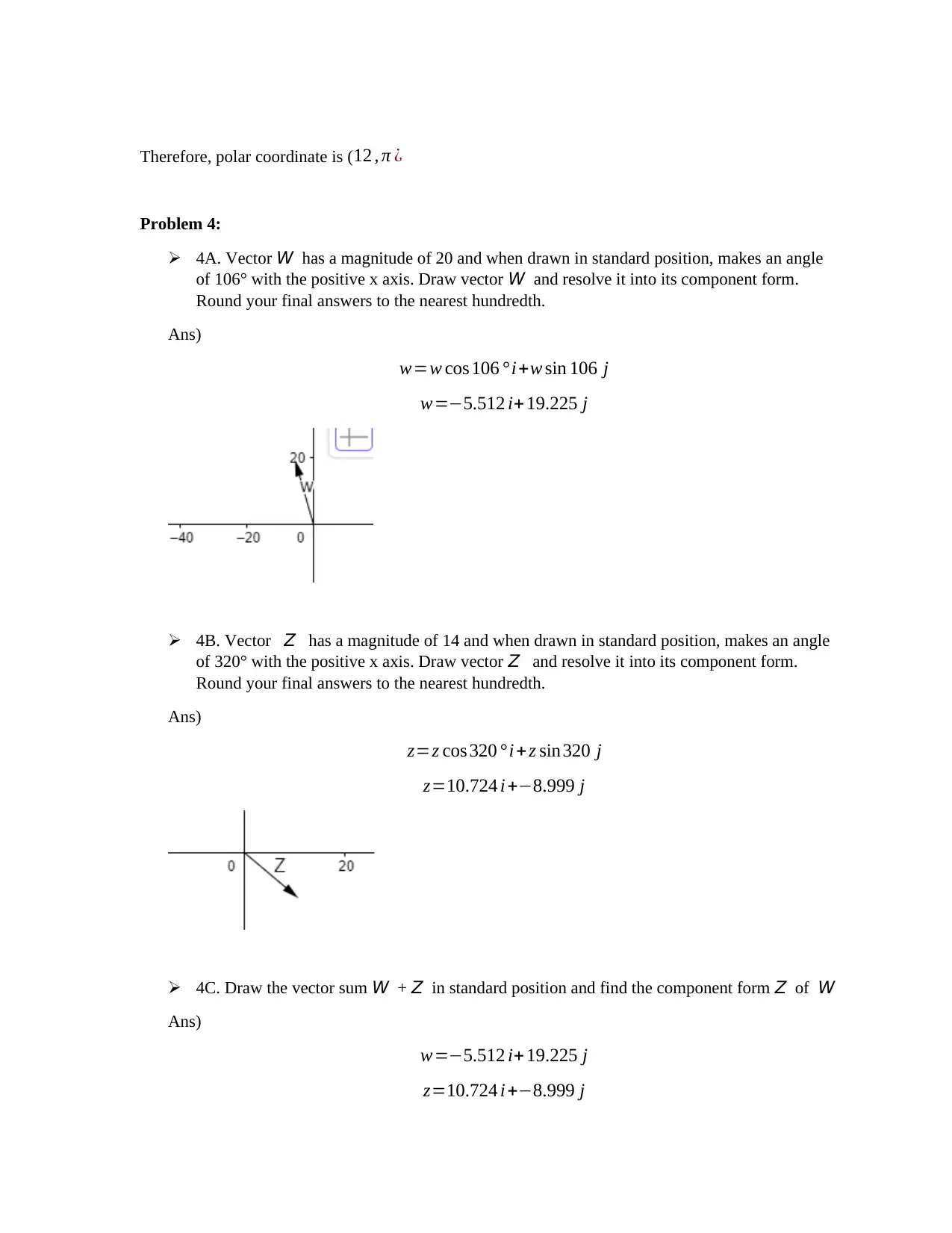
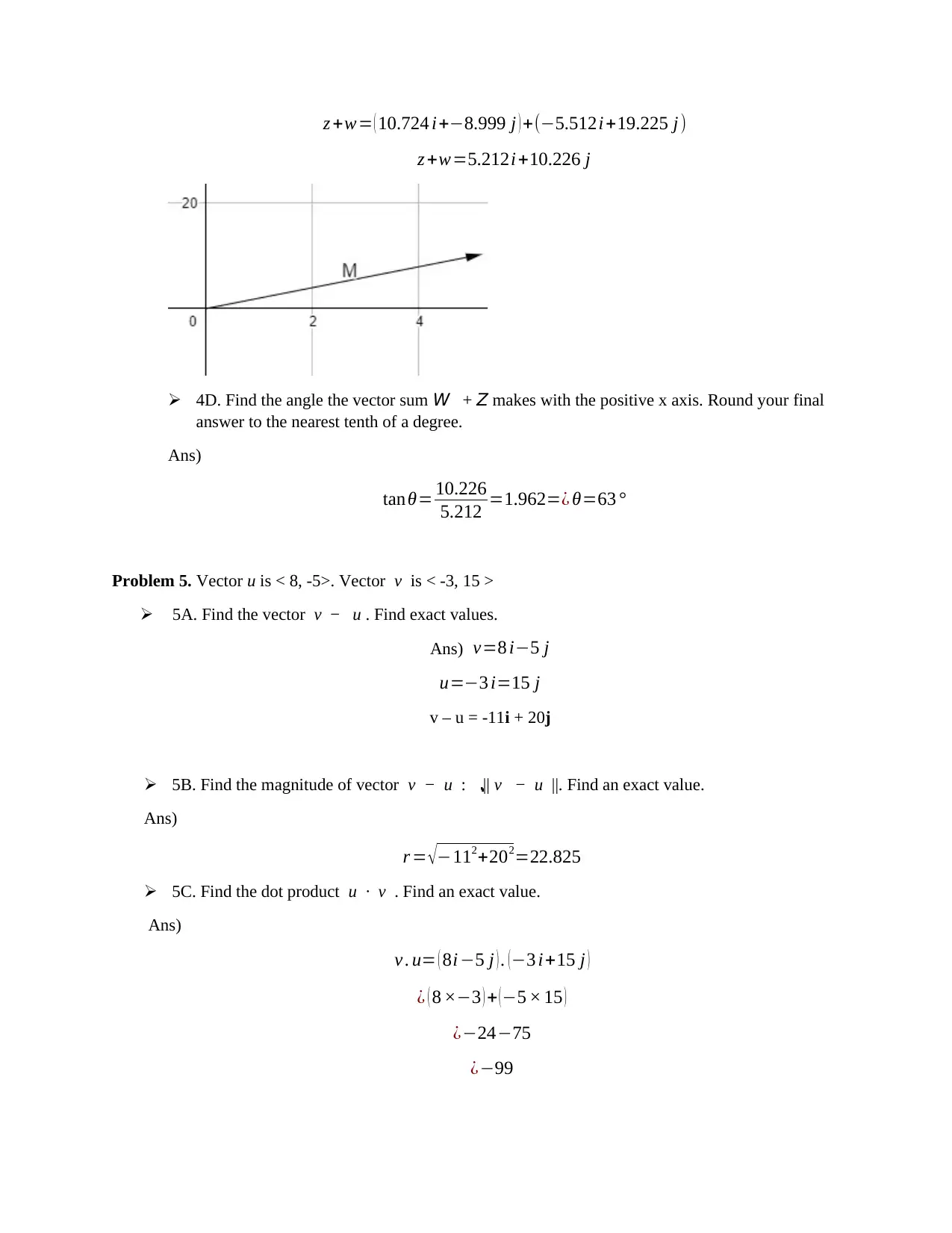








![[object Object]](/_next/static/media/star-bottom.7253800d.svg)