Linear Programming Problems and Solutions

This document contains solved linear programming problems and their solutions. It includes problems related to business decision analysis, production planning, and resource allocation. The solutions are obtained using graphical solution procedure to find the optimal solution and maximize total profit contribution.

BUsiness decision analysis
maths
<student name>
<UNIVERSITY NAME>
APRIL 25, 2019

Individual Problem 3:
Question 10:
For the linear program SELF test
Max 2A + 3B
s.t.
1A+2B ≤6
5A + 3B ≤ 15
A, B ≤ 0
Find the optimal solution using the graphical solution procedure. What is the value of
the objective function at the optimal solution?
Sol.
On plotting the constraints, we get the following graphical output:
Thus, the requires area has only one extreme point, i.e., (0,0)
We can check the objective function only on this point
Putting P(0,0) in 2A + 3B
Max(z) = 0
Checking objective function for any other value in the range, say, (-1,-1)
z= 2(-1) +3(-1)
z = -5
Hence for all other values other than (0,0), z will be negative,
1A+2B ≤
6
5A + 3B ≤
15
A<=0
B<=0

So max value of z will be at P(0,0)
Question 13:
Consider the following linear program:
Max 1A + 2B
s.t.
1A ≤5
1B ≤5
2A + 2B =12
A, B ≤ 0
a. Show the feasible region
Sol.
b. what are the extreme points of the feasible region?
Sol.
Extreme points of the feasible region:
P(5,1) and Q(1,5)
c. Find the optimal solution using the graphical procedure.
Sol. Checking the objective function at P(5,1)
z= 5 + 2(1)
z= 5+2=7
B<=5 A<=
5
2A + 2B =
12 P(5,1)
Q(1,5
)

Checking objective function at Q(1,5)
z=1+2(5)
z=11
Optimal solution = Q(1,5)
Question 14:
Par, Inc., is a small manufacturer of golf equipment and supplies. Par’s distributor be-
lieves a market exists for both a medium-priced golf bag, referred to as a standard
model, and a high-priced golf bag, referred to as a deluxe model. The distributor is so
confident of the market that, if Par can make the bags at a competitive price, the
distributor will purchase all the bags that Par can manufacture over the next three
months. A careful analysis of the manufacturing requirements resulted in the following
table, which shows the production time requirements for the four required
manufacturing operations and the accounting department’s estimate of the profit
contribution per bag:
The director of manufacturing estimates that 630 hours of cutting and dyeing time, 600
hours of sewing time, 708 hours of finishing time, and 135 hours of inspection and
packaging time will be available for the production of golf bags during the next three
months.
a. If the company wants to maximize total profit contribution, how many bags of each
model should it manufacture?
Sol. Let the company manufacture x no Standard of bags and y no of Deluxe bags
Max(z)=10x + 9y
s.t:
7
10 x +1 y ≤ 630
1
2 x+ 5
6 y ≤ 600

x + 2
3 y ≤ 708
1
10 x + 1
4 y ≤ 135
x ≥ 0
y ≥0
We get the value of extreme points as P(0,540), Q(300,420), R(540,250), S(710,0) and
T(0,0)
z(P)=10*0+9*540=4860
z(Q)=10*300+9*420 = 3000+3780=6780
z(R)=10*540+9*250=5400+2250=7650
z(S)=10*710+0*9=7100
z(T)=0
Max(z) is at r(540,250)
For maximized production, the company should produce 540 standard bags and 250
deluxe bags
b. what profit contribution can Par earn on those production quantities?
Sol.

z(R)=10*540+9*250=5400+2250=7650
profit earned = 7650
c. How many hours of production time will be scheduled for each operation?
Sol.
Cutting and Dying
7
10 x +1 y
7
10∗540+250
628 hours
Sewing
1
2 x+ 5
6 y
1
2∗540+ 5
6∗250
270+208.33=478.33 hours
Finishing
x + 2
3 y
540+ 2
3∗250
540+166.66=706.66 hours
Inspection and packaging
1
10 x + 1
4 y
540
10 + 250
4
54+ 62.5
116.5 hours
d. what is the slack time in each operation?
Sol.

Cutting and dying
630−628=2 hours
sewing
600−478.33=121.67 hours
finishing
708−706.66=1.34 hours
inspection and packaging
135−116.5=18.5 hours
Question24:
Kelson Sporting Equipment, Inc., makes two different types of baseball gloves: a regular
model and a catcher’s model. The firm has 900 hours of production time available in its
cutting and sewing department, 300 hours available in its finishing department, and 100
hours available in its packaging and shipping department. The production time
requirements and the profit contribution per glove are given in the following table:
Assuming that the company is interested in maximizing the total profit contribution, an-
swer the following:
a. what is the linear programming model for this problem?
Sol.
Let the company produces x regular model and y catcher’s model
Max(z)=5x+8y
s.t:
x +3
2 y ≤ 900
x
2 + y
3 ≤300

x
8 + y
4 ≤100
x ≥ 0
y ≥0
b. Find the optimal solution using the graphical solution procedure. How many gloves of
each model should Kelson manufacture?
Extreme point coordinates: P(0,400), Q(0,0), R(500,150), S(600,0)
z(P)=5(0)+8(400)=3200
z(Q)=0
z(R)=5(500)+8(150)=2500+1200=3700
z(S)=5(600)+8(0)=3000
Solution:
R(500,150)
c. what is the total profit contribution Kelson can earn with the given production
quantities?
Sol.
Total profit contribution is z(R)=3700
d. How many hours of production time will be scheduled in each department?
Sol.
Cutting and Sewing:

x + 3
2 y
¿ 500+ 3
2 150
500+225=725 hours
Finishing
x
2 + y
3
500
2 + 150
3
250+50=300
Packaging and Shipping
x
8 + y
4
500
8 + 150
4
62.2+37.5=100
e. what is the slack time in each department?
Cutting and Sewing:
900-725=175 hours
Finishing:
30-300= 0 hours
Packaging and Shipping:
100-100=0 hours
Question 36
36. As part of a quality improvement initiative, Consolidated Electronics employees
complete a three-day training program on team building and a two-day training
program on problem solving. The manager of quality improvement has requested that
at least 8 training pro- grams on team building and at least 10 training programs on
problem solving be offered during the next six months. In addition, senior-level
management has specified that at least 25 training programs must be offered during
this period. Consolidated Electronics uses a consultant to teach the training programs.
During the next quarter, the consultant has 84 days of training time available. Each

training program on team building costs $10,000 and each training program on problem
solving costs $8000.
a. Formulate a linear programming model that can be used to determine the number of
training programs on team building and the number of training programs on problem
solving that should be offered in order to minimize total cost.
Sol.
Let the no of training programs on team building be x and the no of no of training
program on problem solving be y
Min(z)=10000x+8000y
s.t:
x ≥ 8
y ≥10
x + y ≥ 25
2 x+3 y ≤ 84
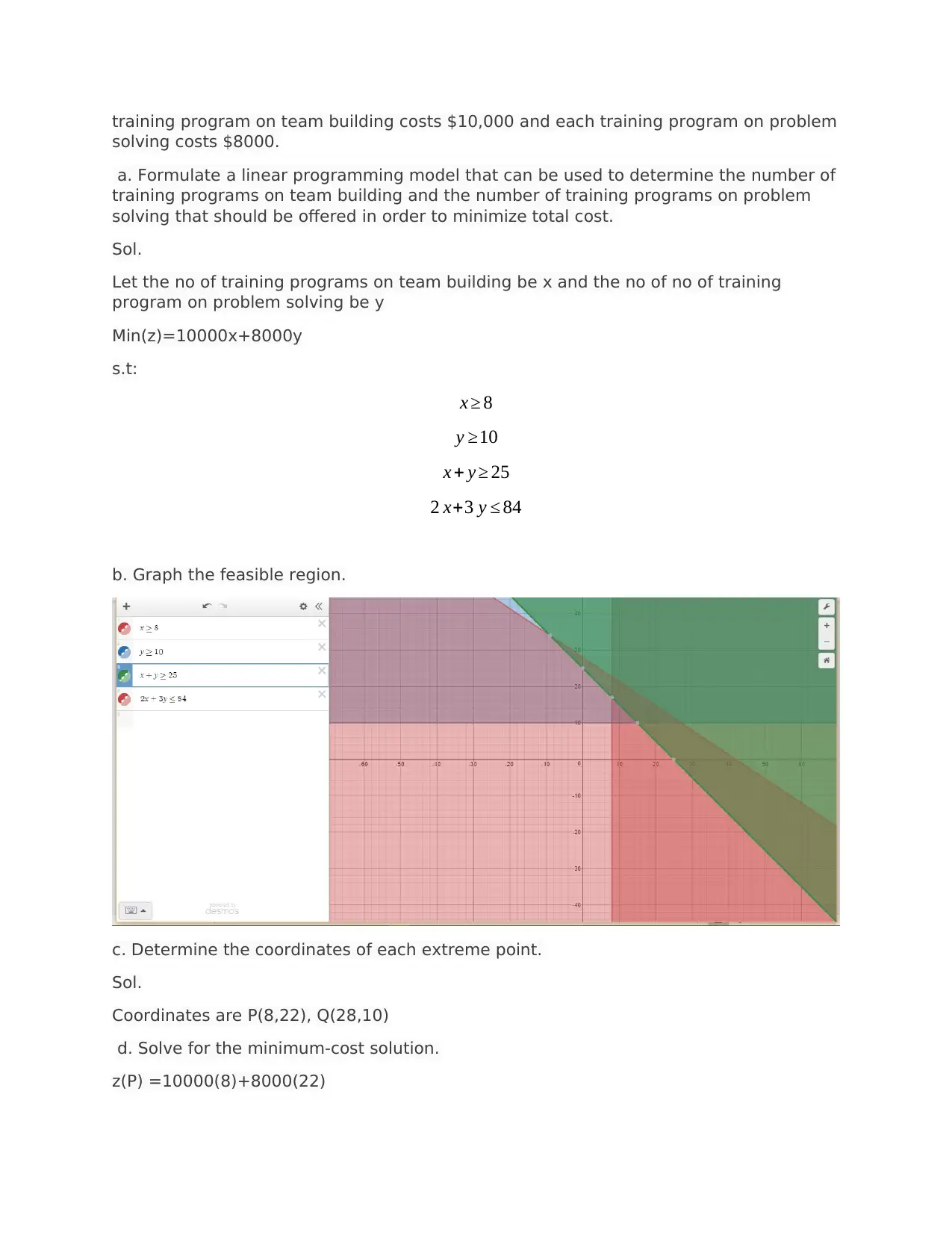
b. Graph the feasible region.
c. Determine the coordinates of each extreme point.
Sol.
Coordinates are P(8,22), Q(28,10)
d. Solve for the minimum-cost solution.
z(P) =10000(8)+8000(22)

=80000+176000
=256000
z(Q)=10000(28)+8000(10)
=280000+80000
360000
Min cost solution =P(8,22)
Question 41:
Southern Oil Company produces two grades of gasoline: regular and premium. The
profit contributions are $0.30 per gallon for regular gasoline and $0.50 per gallon for
premium gasoline. Each gallon of regular gasoline contains 0.3 gallons of grade A crude
oil and each gallon of premium gasoline contains 0.6 gallons of grade A crude oil. For
the next production period, Southern has 18,000 gallons of grade A crude oil available.
The re- finery used to produce the gasolines has a production capacity of 50,000 gallons
for the next production period. Southern Oil’s distributors have indicated that demand
for the premium gasoline for the next production period will be at most 20,000 gallons.
a. Formulate a linear programming model that can be used to determine the number
of gallons of regular gasoline and the number of gallons of premium gasoline that
should be produced in order to maximize total profit contribution.
Sol.
Let the company produces x gallons of regular gasoline and y gallons of premium
gasoline
Max(z)=0.30x+0.50y
s.t:
b. what is the optimal solution? c.
Extreme points: P(0,0),Q(0,20000),R(20000,20000), S(40000,10000), T(50000,0)
z(P)=0
z(Q)=0.3*0+0.5*20000=10000

z(R)=0.3*20000+0.3*20000=12000
z(S)=0.3*40000+0.5*10000=17000
z(T)=0.3*50000=15000
Extreme Value solution = S(40000,10000)
c. what are the values and interpretations of the slack variables?
y=20000-10000=10000
x=0
d. what are the binding constraints?
0.3x+0.6y<=18000
x+y<=50000
y<=20000
x>=0
y>=0