University of Adelaide: Delta-Gamma Hedging on Newcrest Mining ASX
VerifiedAdded on 2023/06/08
|10
|1561
|64
Report
AI Summary
This report details an arbitrage strategy employing delta-gamma neutral hedging on Newcrest Mining Limited (NCM.ASX) from August to September 2018. The strategy leverages a discrepancy between calculated stock volatility (40.98%) and implied volatility (23.30%) of September call options. The implementation involves buying call options and shorting shares to create a delta-neutral portfolio, further refined by incorporating gamma hedging. The report outlines the objectives of delta-neutral hedging, including risk mitigation and continuous portfolio rebalancing. The analysis calculates the profit/loss from the hedged portfolio compared to an unhedged position, highlighting the effectiveness of the strategy in generating a profit of 838.388 AUD. The report also discusses the use of Interactive Brokers for trading and the challenges faced in simulating trades on the Australian market. It concludes that the delta-gamma neutral technique effectively minimizes risk while achieving arbitrage profit. Desklib provides a platform to access similar solved assignments and study resources for students.

PartA
By comparing several companies in the ASX we have chosen Newcrest Mining as it is having one of
the highest P/E ratio in the market(52.5) and moreover it has an active participation in the
derivatives market via the options.
Now we are giving it in a chronological manner
Date:20th August, 2018
We have got by calculating the volatility of the stock must be 40.98% but the implied volatility of the
September Call options whose exercise price is is given as as 23.30%. So here we get the option is
mispriced. We buy the Call Option and go short on Delta number of stocks. The call Price is 0.79
Share Price= 20.62
(a) From the data we got the option delta as 0.61.
Now we have to find the option gamma as part of other Greek
Change in the Price of Call= call delta * (Change in the Price of Stock) + ½ * gamma * (Change
in the stock)^2
Therefore (0.79-0.50) = 0.49* (20.62-20.11) + ½ * gamma * (20.62-20.11)^2
Or, 0.29= 0.2499+ ½* gamma * 0.51^2
Or, gamma= 0.30834
(b) We can do the delta hedging by buying one call and shorting 610 stocks
Number of short call options in order to minimise the effect of Call in Delta Hedging
Portfolio= 0.30834*1=0.30834 =0.31 approx.
So ultimately we get Go long on one Call, short 610 stocks and short 0.31 calls .
(c) The objectives of the portfolio are:
(1) It is used to combine a long position in a call with a short position in a stock so that the
portfolio does not change as the stock price changes.
(2) The main problem of delta-neutral hedging happens to be that the delta hedged asset
position becomes risk free only for a very small change in the value of the underlying stock.
As a result of which the delta-neutral portfolio should be continuously rebalanced in order to
maintain the hedge. As the underlying stock price changes, so the delta of the call option,
and thus the number of calls also need to be changed to maintain a hedged position. Hence,
continuously maintaining a delta-neutral position involves significant transaction costs.
(3)If the assumptions of the Black-Scholes Model hold, changes in the stock price will be
continuous rather than abrupt, and hence there will be no gamma risk. In this context,
gamma can be viewed as a measure of how poorly a dynamic hedge will perform when it is
not rebalanced in response to a change in the asset price. Gamma risk is therefore the risk
that stock price might abruptly jump leaving an otherwise delta-hedged portfolio unhedged.
(d) Now Fast Forward to 6th September
Call Price = 0.30
Share Price = 18.69
So Our net Profit/Loss:
Loss in Calls= (1-0.31)*(0.30-0.79)=(0.3318)=331.8AUD
Profit in Shares=610*(20.62-18.69)=1177.3AUD
So net Profit = 1262.7-33.18= 838.388 AUD
By comparing several companies in the ASX we have chosen Newcrest Mining as it is having one of
the highest P/E ratio in the market(52.5) and moreover it has an active participation in the
derivatives market via the options.
Now we are giving it in a chronological manner
Date:20th August, 2018
We have got by calculating the volatility of the stock must be 40.98% but the implied volatility of the
September Call options whose exercise price is is given as as 23.30%. So here we get the option is
mispriced. We buy the Call Option and go short on Delta number of stocks. The call Price is 0.79
Share Price= 20.62
(a) From the data we got the option delta as 0.61.
Now we have to find the option gamma as part of other Greek
Change in the Price of Call= call delta * (Change in the Price of Stock) + ½ * gamma * (Change
in the stock)^2
Therefore (0.79-0.50) = 0.49* (20.62-20.11) + ½ * gamma * (20.62-20.11)^2
Or, 0.29= 0.2499+ ½* gamma * 0.51^2
Or, gamma= 0.30834
(b) We can do the delta hedging by buying one call and shorting 610 stocks
Number of short call options in order to minimise the effect of Call in Delta Hedging
Portfolio= 0.30834*1=0.30834 =0.31 approx.
So ultimately we get Go long on one Call, short 610 stocks and short 0.31 calls .
(c) The objectives of the portfolio are:
(1) It is used to combine a long position in a call with a short position in a stock so that the
portfolio does not change as the stock price changes.
(2) The main problem of delta-neutral hedging happens to be that the delta hedged asset
position becomes risk free only for a very small change in the value of the underlying stock.
As a result of which the delta-neutral portfolio should be continuously rebalanced in order to
maintain the hedge. As the underlying stock price changes, so the delta of the call option,
and thus the number of calls also need to be changed to maintain a hedged position. Hence,
continuously maintaining a delta-neutral position involves significant transaction costs.
(3)If the assumptions of the Black-Scholes Model hold, changes in the stock price will be
continuous rather than abrupt, and hence there will be no gamma risk. In this context,
gamma can be viewed as a measure of how poorly a dynamic hedge will perform when it is
not rebalanced in response to a change in the asset price. Gamma risk is therefore the risk
that stock price might abruptly jump leaving an otherwise delta-hedged portfolio unhedged.
(d) Now Fast Forward to 6th September
Call Price = 0.30
Share Price = 18.69
So Our net Profit/Loss:
Loss in Calls= (1-0.31)*(0.30-0.79)=(0.3318)=331.8AUD
Profit in Shares=610*(20.62-18.69)=1177.3AUD
So net Profit = 1262.7-33.18= 838.388 AUD
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

So the hedged portfolio I should say is effective. Because we have got a good profit of about
838.388 AUD. The portfolio can be further improved by changing it as we get different delta. But it
will increase the transaction costs. And another reason of the portfolio being effective is that there
was no abrupt jump of the portfolio on that period, though we took up precautionary measure by
shorting gamma number of calls. That’s it.
PartB
Now Fast Forward to 6th September
Call Price = 0.30
Share Price = 18.69
So Our net Profit/Loss:
Loss in Calls= (1-0.31)*(0.30-0.79)=(0.3318)=331.8AUD
Profit in Shares=610*(20.62-18.69)=1177.3AUD
So net Profit = 1262.7-33.18= 838.388 AUD
Now if we had the un-hedged portfolio i.e. buying 610 shares hoping that it will rise, we could have
landed up in 610*(20.62-18.69)=(1177.3)AUD loss
We have taken 61 share by virtue of the formula below:
Number of Call options needed to delta hedge= Number of shares hedged/Delta of Call option
(Mind that it is not Call Option Contract)
i.e. Number of shares hedged= Number of Call Options to delta hedge*Delta of Call Option
=1000*0.61=610
The delta-hedging strategy is superior due to the following reasons:
1. It hedges away the unwanted risks involved.
2. It helps in gaining the exposure to volatility and not price.
3. It helps the trader to be non-directional instead of being directional, as directional trading
strategies are very risky
838.388 AUD. The portfolio can be further improved by changing it as we get different delta. But it
will increase the transaction costs. And another reason of the portfolio being effective is that there
was no abrupt jump of the portfolio on that period, though we took up precautionary measure by
shorting gamma number of calls. That’s it.
PartB
Now Fast Forward to 6th September
Call Price = 0.30
Share Price = 18.69
So Our net Profit/Loss:
Loss in Calls= (1-0.31)*(0.30-0.79)=(0.3318)=331.8AUD
Profit in Shares=610*(20.62-18.69)=1177.3AUD
So net Profit = 1262.7-33.18= 838.388 AUD
Now if we had the un-hedged portfolio i.e. buying 610 shares hoping that it will rise, we could have
landed up in 610*(20.62-18.69)=(1177.3)AUD loss
We have taken 61 share by virtue of the formula below:
Number of Call options needed to delta hedge= Number of shares hedged/Delta of Call option
(Mind that it is not Call Option Contract)
i.e. Number of shares hedged= Number of Call Options to delta hedge*Delta of Call Option
=1000*0.61=610
The delta-hedging strategy is superior due to the following reasons:
1. It hedges away the unwanted risks involved.
2. It helps in gaining the exposure to volatility and not price.
3. It helps the trader to be non-directional instead of being directional, as directional trading
strategies are very risky
REPORT WRITING
Title: A report on the arbitrage Profit made by the delta-hedging technique on the Newcrest
Mining Limited stock on the S&P ASX stock Market.
Introduction: Delta-hedging technique is a well-known technique to minimise the unwanted
risk in any portfolio. An arbitrage profit can be made based on this technique. To minimise
the exposure of Delta we added the gamma factor and made it a Delta-Gamma Neutral
Hedging Technique. In order to this we should have a stock which has a very high P/E so as
to get stability in the portfolio. There should be a presence of the stock in the options market.
Based on these we got Newcrest Mining Limited NCM.ASX as the most suitable stock
Body:
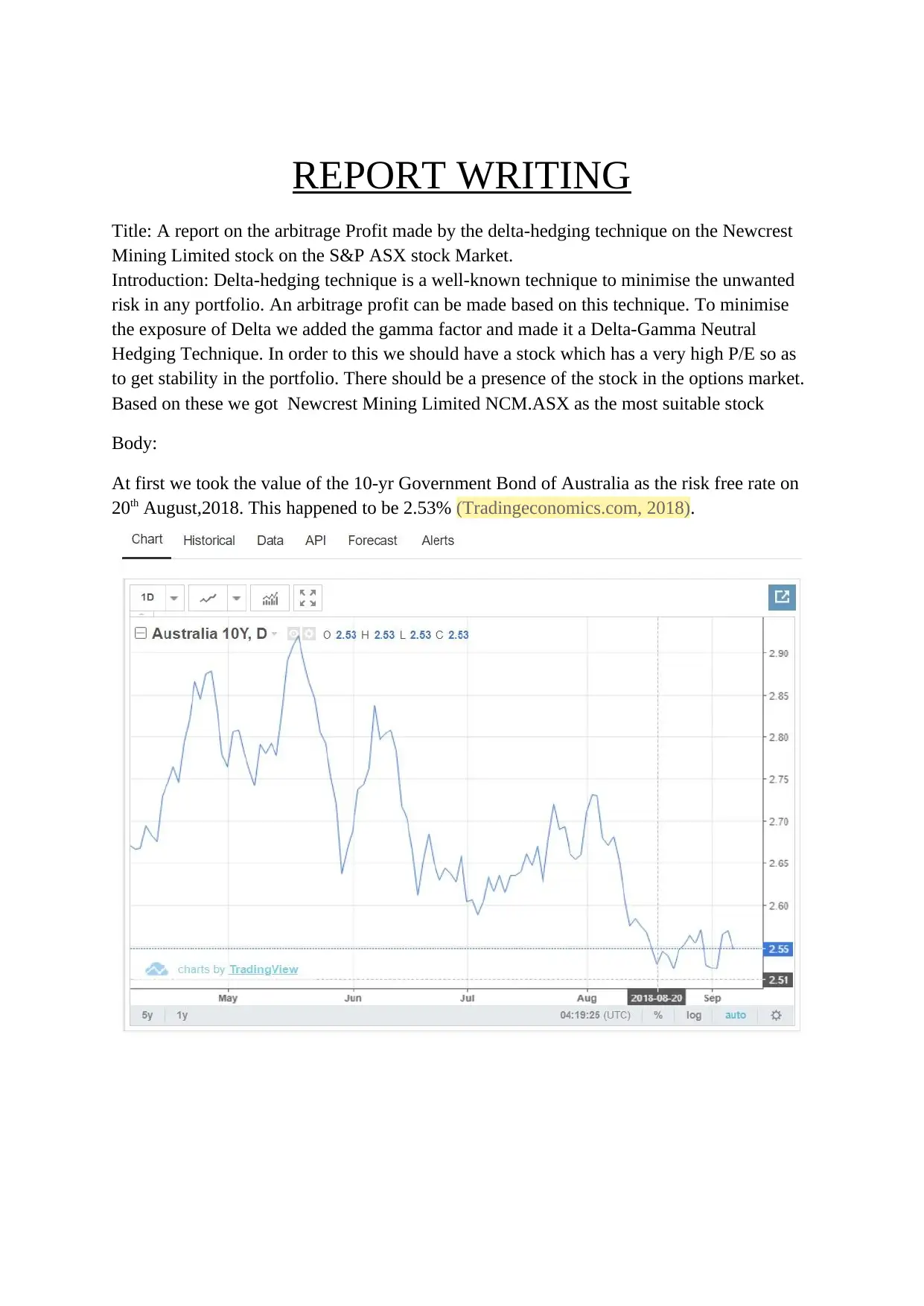
At first we took the value of the 10-yr Government Bond of Australia as the risk free rate on
20th August,2018. This happened to be 2.53% (Tradingeconomics.com, 2018).
Title: A report on the arbitrage Profit made by the delta-hedging technique on the Newcrest
Mining Limited stock on the S&P ASX stock Market.
Introduction: Delta-hedging technique is a well-known technique to minimise the unwanted
risk in any portfolio. An arbitrage profit can be made based on this technique. To minimise
the exposure of Delta we added the gamma factor and made it a Delta-Gamma Neutral
Hedging Technique. In order to this we should have a stock which has a very high P/E so as
to get stability in the portfolio. There should be a presence of the stock in the options market.
Based on these we got Newcrest Mining Limited NCM.ASX as the most suitable stock
Body:
At first we took the value of the 10-yr Government Bond of Australia as the risk free rate on
20th August,2018. This happened to be 2.53% (Tradingeconomics.com, 2018).
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

The volatility (or standard deviation) of the stock based on last 18 trading days, has been
calculated by virtue of the Microsoft Excel stdev() formula and is found to be 0.4098.
calculated by virtue of the Microsoft Excel stdev() formula and is found to be 0.4098.
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
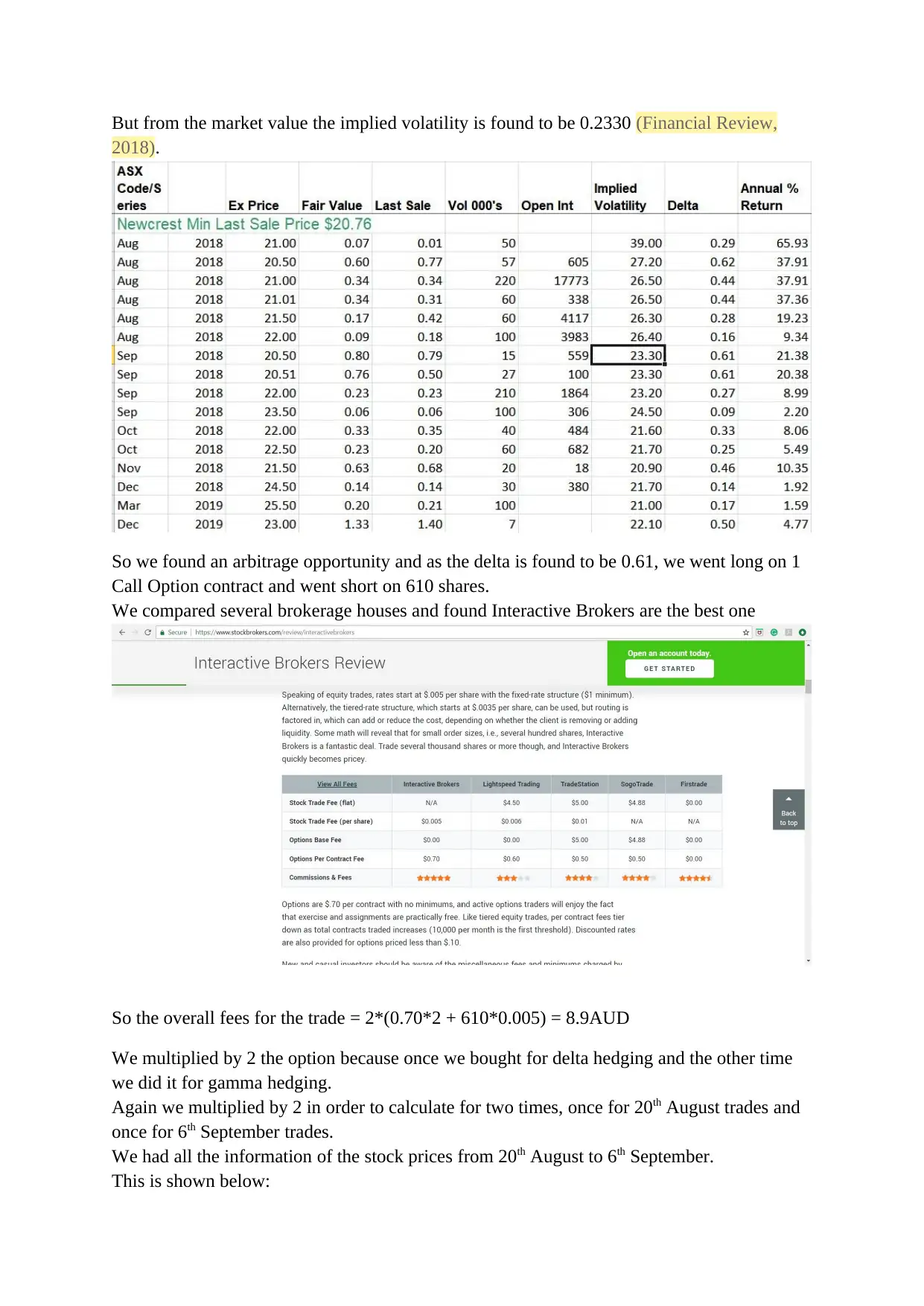
But from the market value the implied volatility is found to be 0.2330 (Financial Review,
2018).
So we found an arbitrage opportunity and as the delta is found to be 0.61, we went long on 1
Call Option contract and went short on 610 shares.
We compared several brokerage houses and found Interactive Brokers are the best one
So the overall fees for the trade = 2*(0.70*2 + 610*0.005) = 8.9AUD
We multiplied by 2 the option because once we bought for delta hedging and the other time
we did it for gamma hedging.
Again we multiplied by 2 in order to calculate for two times, once for 20th August trades and
once for 6th September trades.
We had all the information of the stock prices from 20th August to 6th September.
This is shown below:
2018).
So we found an arbitrage opportunity and as the delta is found to be 0.61, we went long on 1
Call Option contract and went short on 610 shares.
We compared several brokerage houses and found Interactive Brokers are the best one
So the overall fees for the trade = 2*(0.70*2 + 610*0.005) = 8.9AUD
We multiplied by 2 the option because once we bought for delta hedging and the other time
we did it for gamma hedging.
Again we multiplied by 2 in order to calculate for two times, once for 20th August trades and
once for 6th September trades.
We had all the information of the stock prices from 20th August to 6th September.
This is shown below:

We went long on the (1-0.31) call options and went short on 610 stocks on 20th August, 2018.
And we sold the entire Portfolio on 6th September.
The chart (Finance.yahoo.com, 2018) is shown below:
And we sold the entire Portfolio on 6th September.
The chart (Finance.yahoo.com, 2018) is shown below:
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

The total Profit of this portfolio we calculated is 1229.52AUD. But unfortunately we did not
calculate the brokerage amount. So after adjusting the brokerage amount we get,
1229.52-8.9= 1220.62AUD.
We used the Interactive Brokerage account to do the trading in their Trader Workstation
Platform. As it is a demo account and Australian Markets are not allowed in the demo
account so unfortunately we could not perform the real trading. Some of the situations are
shared below.
The screen of the demo account looks like this:
calculate the brokerage amount. So after adjusting the brokerage amount we get,
1229.52-8.9= 1220.62AUD.
We used the Interactive Brokerage account to do the trading in their Trader Workstation
Platform. As it is a demo account and Australian Markets are not allowed in the demo
account so unfortunately we could not perform the real trading. Some of the situations are
shared below.
The screen of the demo account looks like this:
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
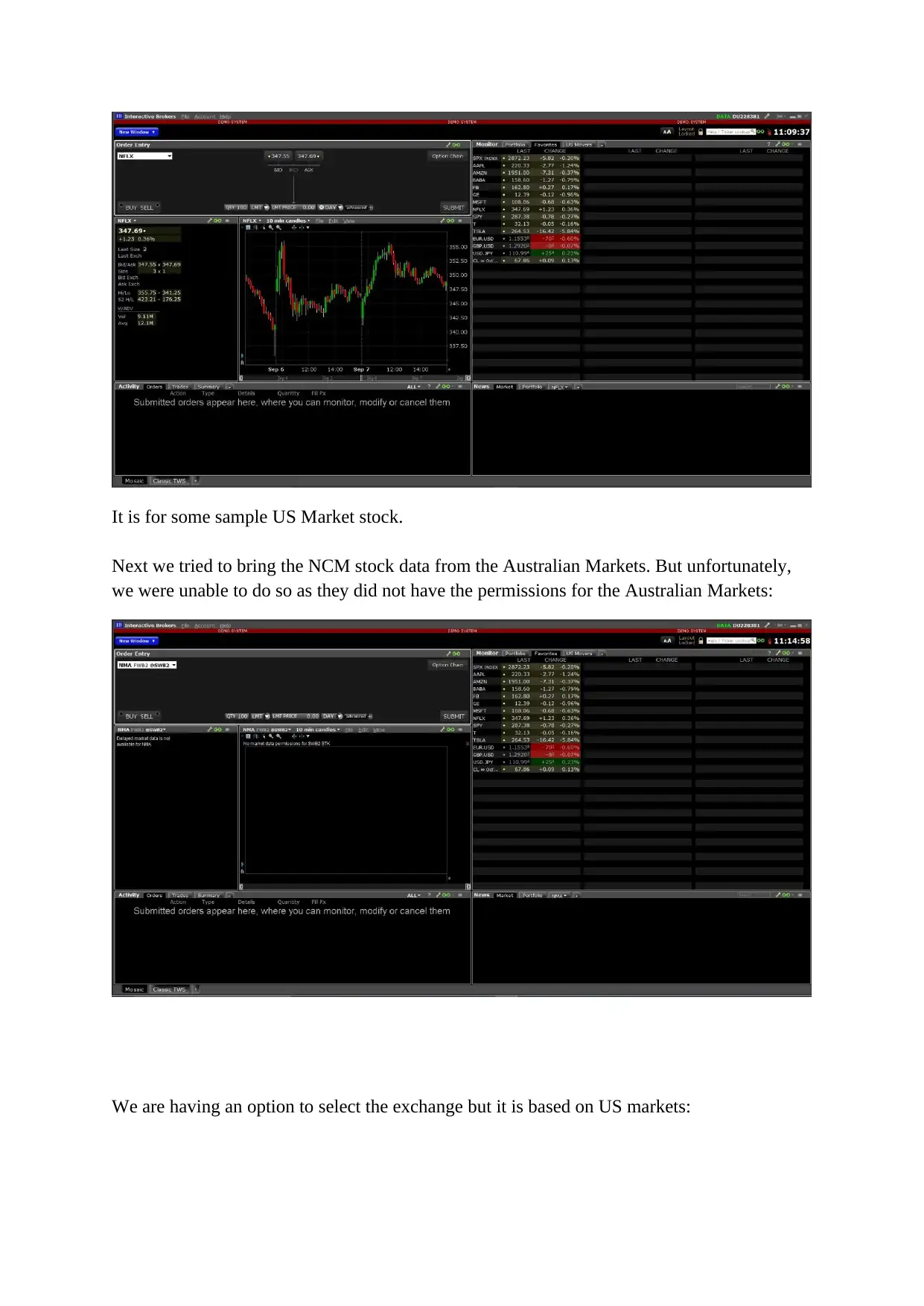
It is for some sample US Market stock.
Next we tried to bring the NCM stock data from the Australian Markets. But unfortunately,
we were unable to do so as they did not have the permissions for the Australian Markets:
We are having an option to select the exchange but it is based on US markets:
Next we tried to bring the NCM stock data from the Australian Markets. But unfortunately,
we were unable to do so as they did not have the permissions for the Australian Markets:
We are having an option to select the exchange but it is based on US markets:
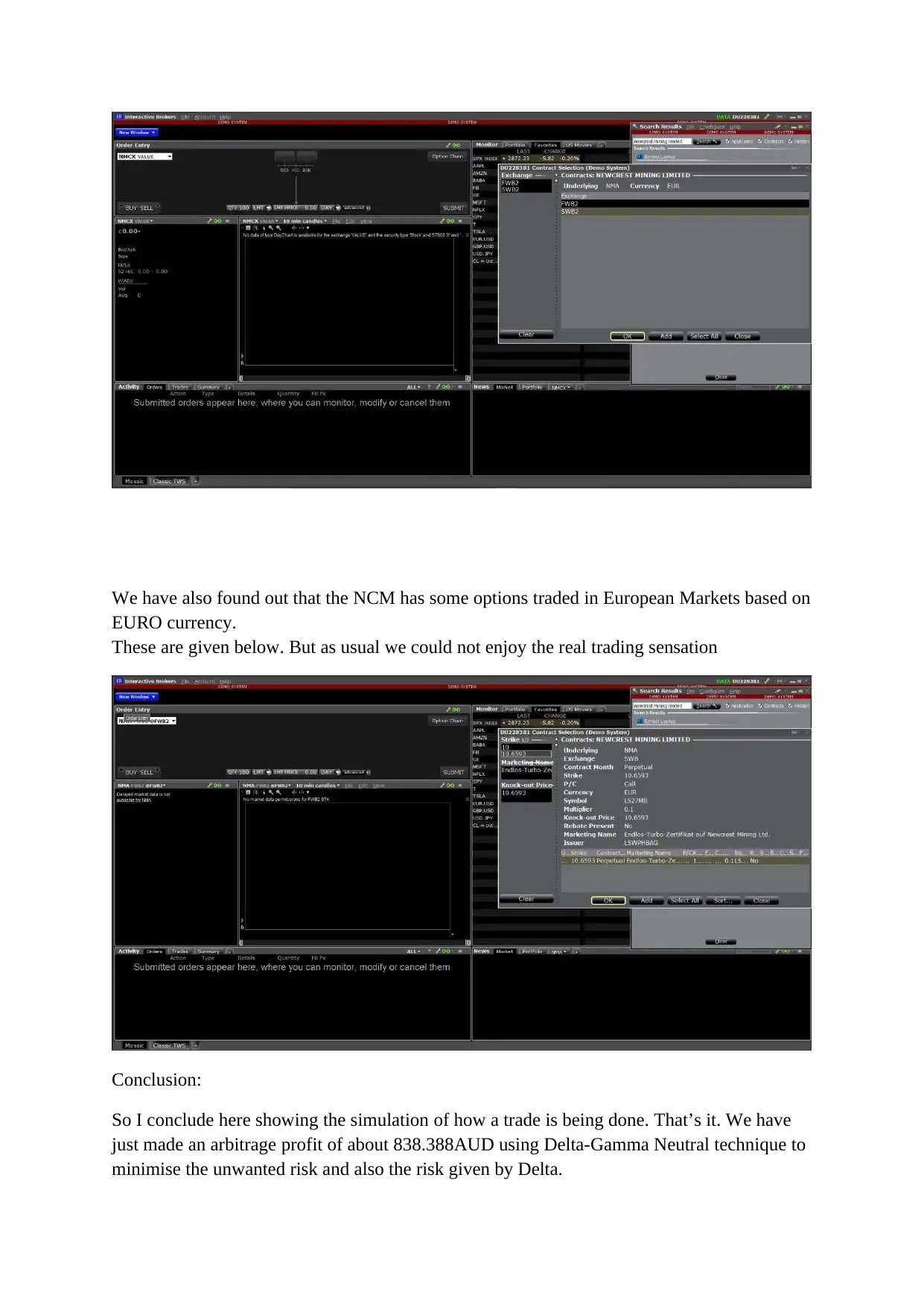
We have also found out that the NCM has some options traded in European Markets based on
EURO currency.
These are given below. But as usual we could not enjoy the real trading sensation
Conclusion:
So I conclude here showing the simulation of how a trade is being done. That’s it. We have
just made an arbitrage profit of about 838.388AUD using Delta-Gamma Neutral technique to
minimise the unwanted risk and also the risk given by Delta.
EURO currency.
These are given below. But as usual we could not enjoy the real trading sensation
Conclusion:
So I conclude here showing the simulation of how a trade is being done. That’s it. We have
just made an arbitrage profit of about 838.388AUD using Delta-Gamma Neutral technique to
minimise the unwanted risk and also the risk given by Delta.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

References:
Tradingeconomics.com. (2018). Australia Government Bond 10Y | 1969-2018 | Data |
Chart | Calendar. [online] Available at:
https://tradingeconomics.com/australia/government-bond-yield [Accessed 8 Sep. 2018].
Financial Review. (2018).ASX Share Tables [online] Available at:
http://www.afr.com/share-tables [Accessed 8 Sep. 2018].
Finance.yahoo.com. (2018). Yahoo Finance NML.AX. [online] Available at:
https://finance.yahoo.com/quote/NCM.AX/history?p=NCM.AX [Accessed 8 Sep. 2018].
Tradingeconomics.com. (2018). Australia Government Bond 10Y | 1969-2018 | Data |
Chart | Calendar. [online] Available at:
https://tradingeconomics.com/australia/government-bond-yield [Accessed 8 Sep. 2018].
Financial Review. (2018).ASX Share Tables [online] Available at:
http://www.afr.com/share-tables [Accessed 8 Sep. 2018].
Finance.yahoo.com. (2018). Yahoo Finance NML.AX. [online] Available at:
https://finance.yahoo.com/quote/NCM.AX/history?p=NCM.AX [Accessed 8 Sep. 2018].
1 out of 10
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.


