ASME Division 2 Rules for Pressure Vessel Design: Local and Global Failure Analysis

This article discusses the ASME Division 2 rules for pressure vessel design and analysis of local and global failure. It covers the procedures for buckling load, collapse load, limit of strain, ultimate strength, and yield strength. It also talks about the design of pressure vessels, types of failure, stress-strain analysis, and more. The article includes literature review, background of the code, local and global failure analysis, elastic-plastic analysis, types of failure, and more.

Name of the Student
Name of the Professor
City/State
Date/Month/Year

Introduction
The procedures and defines the allowable for buckling load, collapse load, the limit of the strain,
ultimate strength and yield strength are articulated in the ASME Division 2 rules. These
procedures are based on protection against failure models for example protection against collapse
from bulking and also safeguard contrary to local failure.
The requirement for local failure procedure is articulated in ASME division, and also it defines
the allowable yield strength, ultimate strength, strain limit, collapse load and buckling load that
needs to be satisfied. These procedures are based on protection against failure modes which are
guarded alongside local failure modes, plastic downfall, and protection against failure of
buckling. The procedure called out may be applied if the stress evaluated at the design
temperature is governed by time-independent properties unless it is allowed by specific design
procedure. The difference in material properties and variations in loading is accounted for by
load factors account. In the case of defense in contradiction of plastic failure, three alternate
approaches are allowed to be used. Aiming at determining an inferior guaranteed to the limit
weight of a component then the limit load method is preferred.
The limit load analysis articulates the manner in which the failing of rapture in malleable and the
commencement of plastic distortion of a building. The ASME also requires that in addition to
evaluating defense from plastic failure or from buckling, it shall be pleased to evade buckling of
constituents with a compressive stress field under applied design loads.

Literature Review
According to the research conducted by the International Journal of Research in Science and
Engineering, the fatigue analysis of a reactor pressure vessels is performed using heat transfer
coefficient based on operating environment. The overall stress intensity range is investigated to
determine the adequacy of design. The material of a pressure vessel may be brittle for example
ductile or cast iron. The failure behavior of pressure vessels during high pressure has been
investigated experimentally and the result showed that the pressurization rate and acoustic
emission response to the vessels to the pressure loading.
A practical analysis method was conducted by Hoyt et al (2003) for the power, toughness and
damage easiness assessment of compound. Strength-of-materials failure criteria assist in
predicting serious injury instigation weights and situations. A fracture mechanics technique is
applied in predicting destruction development and failure based on motionless and cyclic loads
based on test data for static fracture hardiness and crack rate of growth.
Instigation and development of matrix cracks produced AE events having low duration and low
energy as investigated by Surgeon et al (1997). The smaller period events could be accredited to
micro-cracks, a procedure by which was accompanied by deboning of matrix/fiber-matrix
interface. The formation of macro and micro-cracks could be resolved in the case of
unidirectional material.
Background of the code
The ASME Boiler and Pressure vessel code were created to regulate the design and construction
of pressure vessels and boilers. It was formed after numerous serious explosions in the state of
Massachusetts. The first edition of this code was in 1914 after which the verification that the
manufacturer was to the code was performed by independent inspectors causing numerous

interpretations. The rules are provided by the code cases allowing the material use and
alternative methods of constructions.
Design of pressure vessels
The ASME governs the design of pressure vessels and the designing of pressure vessels is
carried out so that to contain pressure and withstand operating mechanically. Pressure vessels
maybe lined with numerous ceramics, polymers, and metals to prevent leakage and materials
needed for the construction, and should have properties such as heat resistant, high tensile
strength and resisting maximum stress.
Designing of spherical pressure vessel design is typically stronger compared to cylindrical shape,
with the same wall thickness through the spherical ones which are very expensive when it comes
to manufacturing and pressure vessels are typically made of steel and according to ASME
Section VIII, Division 1, design-by-rule approach is the most commonly used by engineers to
size the pressure vessels. In division 2 consist design-by-analysis approach while the third
decision entails pressure vessels that need internal or external operating pressure above 10,000
PSI. In order to size a pressure vessel then the following data is required by the engineer which
include;
Vessels function, operating conditions, materials of construction and operating conditions.
LOCAL FAILURE
The description against local failure is articulated in section 5.3 of the ASME. The chosen
method uses the elastic-plastic analysis and compares the total equivalent plastic strain to a
limiting strain (Wadsworth, 2009, p. 156). The material model requires that the effect of non-
linear geometry is included. The local failure requires the use of non-linear geometry with a load

factor. The arc length procedure and gradually applied procedure are used in the local criteria so
that non-linear geometry and plastic effects would be accounted for properly (Dieter, 2014, p.
347).
The yield condition currently available and it is suitable for ductile materials for example metals
like aluminum and steel. The plastic behavior of materials may be combined with other types of
non-linearity (Kotelyanskii, 2008, p. 341). The von Mises yield criterion proposes that the
materials yielding begin when the critical value is attained by the additional deviatory stress
invariant. The von Mises criterion is appropriate for examination of plastic distortion for
materials which are ductile such as metals because it is independent of the primary stress
invariant (Chirag, 2015, p. 67).
In nonlinear properties of materials, the selected material will behave elastically during a non-
linear analysis, and plasticity can be enabled by selecting a type of plastic behavior (Hertzberg,
2012, p. 459). It corresponds to the bilinear stress-strain relationship, identical in tightness and
compression. The stress-strain relationship is automatically generated by three parameters which
are elastic part or young modulus, yield stress and slope of the elastic branch (Li, 2008, p. 500).
Plasticity simply defines the distortion of a material in solid form going through changes in
shape which cannot be reversed as a result of forces applied. In case of a metal solid in the state
being pounded or bent forming a fresh outline, shows plasticity as lasting variations arise in the
interior the material itself (Goh, 2016, p. 200). Plasticity is mostly observed in materials for
example soils, rocks, metals and many others and in metals, plastic deformation always comes as
a result of dislocations which is rare in crystalline materials (Li, 2007, p. 456).

In ductile materials, stretchable loading used in a sample will make the material in a mutable
way. For each increase of load is escorted by a relative increase in extension and in case of
removing the load, the part goes back to its original size (Hiermairer, 2007, p. 652). In case the
weight surpasses the threshold, the yield strength, the allowance upsurges more quickly than
inelastic area and removal of the load, a certain grade of allowance will remain (Pullan, 2007, p.
67).
Global failure
Distortion of elastic is an estimation and its superiority rely on the time deliberated and the speed
of loading. Plasticity or malleability is a property of materials to go through irreparable distortion
deprived of any increase in loads and stresses (Kohser, 2013, p. 54). Plastic hardening involving
hardening which requires progressively advanced stresses to cause in extra plastic distortion. The
material plasticity relative to the material ductility, malleability and most plasticity in metals is
chiefly triggered by two nodes of distortion, which assist in atoms movement over many
interatomic spaces comparative to their original locations. Most plasticity is shown in metals
mostly when they are hot than when they are cold (Moavenzadeh, 2016, p. 531).
The origins of soil malleability are multifaceted fairly and powerfully relies on the
microstructure chemical conformation, and the gratified of water (Besson, 2009, p. 188).
Plasticity performance in soils is triggered mostly by reorganization of clusters of head-to-head
grains while inelastic deformations of rock are mostly instigated through the creation of minor
cracks and sliding motions comparative to these cracks (Mai, 2009, p. 319). There are three
alternative techniques which are used in evaluating the structure used in protecting material
against plastic collapse and they include elastic stress analysis approach and elastic-plastic stress
analysis.

Plasticity related failure
a). Under static load
The static loads simply mean that particular load which is applied slowly and remain constant
without any change for a long duration of time. Loads do not cause static failure but the failure is
caused by two factors which include the constructional features and the material. Elongation of
material taking place more than 5% of its length is known as ductile material while those
elongating before attaining 5% are referred to them as brittle material (Broek, 2013, p. 335).
b). under Limit load
This is a situation whereby the load acting on a structure is increasing proportionally at some
point it reaches a certain critical value at which the plastic failure of the structure occurs after
which the structure is unable to receive the further accrual of the load. The elastic deformation
which is caused by materials depends on the speed of loading and the time frame. In a situation
where the material suffers from irreversible deformation, the material has a property known as
perfect plasticity which takes place without any increase in loads or stresses (Reginald, 2010, p.
77)
c). Elastoplastic loads
There is elastic behavior exhibited by different metals for small loads. Further increase in load
makes the material to undergo plastic deformation. Elastoplastic material selects isotropic as the
symmetry type and selects elastoplastic as the stress-strain response. The deformations caused as
a result of internal stresses are linearly related to the applied loads. And linearity cannot be
assumed though internal forces distribution included by applied loads and which are affected by
the built-in stress such that it changes the material stiffness and also a failure of material which

was not expected. In order to get rid of the built-in stress, it is necessary to conduct annealing of
metal parts (Tomlinson, 2014, p. 74).
Loss of ductility
The ductility is simply the ability of a material to undergo significant plastic deformation before
rupture. The temperature at which the fracture energy passes below a predetermined value is
known as the ductile-brittle transition temperature and this type of temperature is important since
once the material is cooled below the DBTT, it has a much greater tendency to shatter on impact
instead of deforming or bending. The fracture testing is the most accurate method of use in
measuring the material DBTT (Bower, 2009, p. 125).
Stress-strain analysis
The stress-strain analysis which is also known stress analysis uses many methods in determining
the strain and stresses in materials and structures subjected to forces (Noon, 2008, p. 54). The
stress analysis involved in designing the structure of all sizes for example bridges and tunnels.
The stress analysis is used in investigating the causes of structural failure and also maintenance
of structures (Kohser, 2013, p. 89). The description of the properties and structure of the
material, how the parts are joined and the expected typical or maximum force are the stress
analysis starting point (Hertzberg, 2012, p. 789). Any force acting externally on a material needs
to be balanced by the internal reaction forces which cause acceleration of particles and the
substantial move is needed in order to enable the material to uphold its shape (Pullan, 2007, p.
56). Application of force on one part of a material causes an increase in internal reaction forces
assisting in the propagation of particles to particles (Revie, 2008, p. 195)

Elastic-Plastic analysis
The non-reversible changes undergone by various materials are described by this method. Plastic
deformation is mostly observed in soil, metals, and rocks though plastic deformation caused by
physical mechanism vary widely (Fassi, 2017, p. 890). The materials behave in an elastic manner
during the application of tensile loading in ductile metals since extension accompanies the load
increment. The materials face irreversible or plastic deformation in case the critical value is
exceeded (Beckmann, 2012, p. 609).
Local Elastic-Plastic Analysis
The local criteria are most likely to be violated in the region of notches such that high local stress
concentration factor will probably have low strain limit.
Elastic-plastic limit analysis acceptance criteria
A buckling analysis is required for components subjected to a comprehensive stress field and
also a ratcheting analysis is required whereby the loads are applied and removed in the proper
sequence and one of the following criteria must be met;
 No cyclic plasticity
 No permanent change in overall dimensions.
 The elastic core remains in the primary load bearing
boundary.
Fatigue Analysis – Fracture Mechanics Method
The assumption in the fracture mechanics method is that a flaw exists at the most highly stressed
locations in the structure immediately after construction.
Effects of Axial Stress on Through-Thickness Yield Pressure

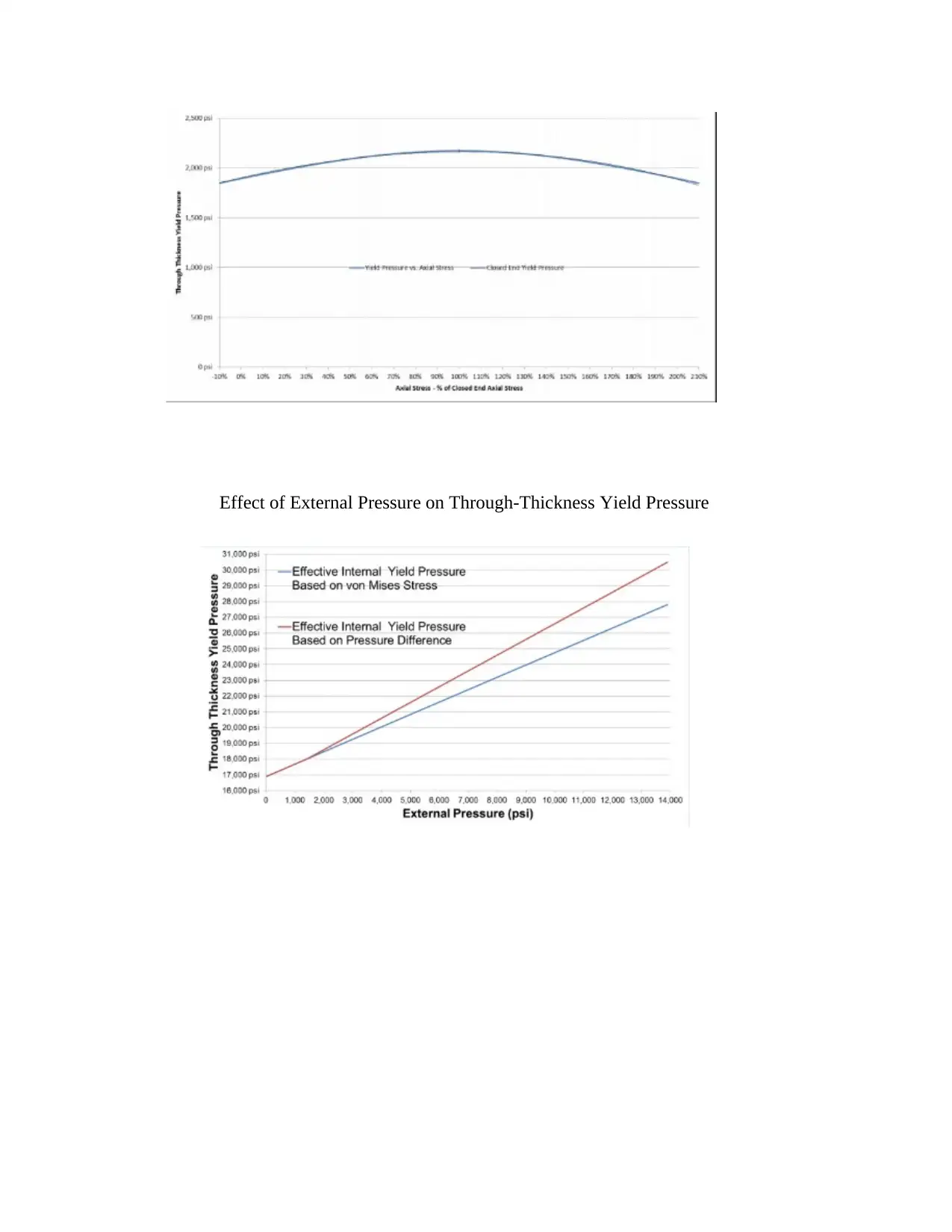
Effect of External Pressure on Through-Thickness Yield Pressure

Types of failure
They are different types of material failure, for example, yielding, fracture, elastic deformation,
wear, bu-concentration, cackling, corrosion, stress and caustic embrittlement.
Yielding
A yield point is a stress at which deforming of a material starts plastically. The deformation of
material will take place elastically and goes back to its original shape after the removal of the
stress applied. The yield point curves for the stress-strain indicating the limit of elastic
performance and the commencement of plastic performance (Sammy, 2009, p. 32) There are
certain fraction of the distortion which will be everlasting and cannot be reversed after the yield
point is passed. (Kuna, 2013, p. 98). The limits of performance for mechanical components is
determined by the yield point and this type of failure does not cause the ultimate or catastrophic
failure unless accelerated by buckling and that is the reason it is referred as a soft failure mode
(Askeland, 2015)
Fracture
The tensile stress involving plastic deformation is categorized by a strain hardening area and a
necking region and finally which is also known as rupture. Crack is simply the parting material
in binary or extra pieces when the act upon them. (Revie, 2008, p. 763). The solid fracture
normally takes place as a result of the growth of particular movement disjoining the exteriors
within the solid. A normal tensile crack comes as a result of the growth of displacement
perpendicular to the surface of displacement and the shear crack is when the dislodgment
develops tangentially to the surface of displacement (Kotelyanskii, 2008, p. 23).

The breaking strength or the strength of the fracture is the stress when a sampling fracture or
fails and it can be determined by the tensile test. The fracture strength of the ductile materials is
lower compared to the final elastic strength such that, in inelastic material, the strength of the
fracture is conforming to the closing elastic strength. A ductile material continues deforming in
case it attains the final tensile strength in a load-controlled situation. Though, the distortion of
the material may dismiss the weight, stopping the disagreement if in case the loading is
displacement-controlled (Hiermairer, 2007, p. 720).
In ductile fracture, wide plastic distortion occurs before rupturing of the fracture and the ductile
defines the ultimate failure of ductile materials loaded in tension. Since the ductile rupture entails
a great point of plastic distortion, the conduct of a fracture of a spreading crack varies basically.
The ductile fracture steps involve the following basic steps which include; formation of a void,
void coalescence which is also referred to as formation of a crack, then crack propagation and
failure (Courtney, 2008, p. 654).
Elastic deformation
This is a type of reversible deformation whereby the object goes back to its original shape when
the forces applied are withdrawn. Huge elastic deformation ranges are exhibited by the
elastomers and memory metals mostly, and also rubber. Smaller elastic range and linear
elasticity are shown by the ceramics, normal metals and most crystals.
Buckling
Buckling is considered by an unexpected failure of a physical member exposed to high
compressive stress where the real compressive stress at the point of failure is less than the
ultimate compressive stresses that the material is capable of withstanding for example during

earthquake, reinforced concrete members may experience lateral deformation of the longitudinal
reinforcing bars (Noon, 2008, p. 542).
Stress concentration
This discrepancy is explained by the presence of very small cracks or microscopic flaws that are
inherent to the material. (Pullan, 2007, p. 45) An even distribution of the force over its area
makes an object stronger, and material failure takes place via a spreading crack when intense
upsurge the materials imaginary combined strength (Byfield, 2018, p. 678). The fatigue strength
of a material normally falls below proposed value, because small contaminants are contained in
many materials that ponder stress and the fatigue cracks always start at stress raisers, so
eliminating such flaws upsurges the exhaustion strength (Tomlinson, 2014, p. 76).
The prediction of material failure is done using failure theory which predicts the circumstances
where materials in solid form fail under the act of exterior weights (Grupta, 2017, p. 76). The
ductile (yield) or brittle (fracture) are usually used in classifying material failure, though they
depend on certain conditions such as rate of loading, temperature, and stress state. Several
materials can fail in a state of ductile or brittle or even together (Holdsworth, 2008, p. 34).
Material failure in simple terms can just be defined as the forfeiture of the weight supporting
volume of a material unit, and the examination of material failure can be done in dissimilar
scales starting from microscopic to macroscopic (Askeland, 2015, p. 219). In structural
problems, where the structural response maybe beyond the initiation of nonlinear material
behavior, the material is of profound importance for the determination of the integrity of the
structure (Hiermairer, 2007, p. 319).

The distinguishing of failure of materials is done in two different wide groups based on the scale
in which the examination of the material takes place. They include;
Microscopic failure
Microscopic failure of material is simply distinct in positions of crack initiation and propagation.
This type of method is necessary for acquiring an understanding of the specimen cracking and
humble assemblies under well-tackled comprehensive load deliveries. In this area, the greatest
known models of failure are micromechanical failure models that bring together the advantages
of classical fracture and range mechanism. Such models rely on the concept that in the case of
plastic distortion, microvoids come together and develop till the neck of the inner void matrix
takes place causing the joining of neighboring voids (Woodward, 2017, p. 543).
Macroscopic failure
Macroscopic materials failure is simply defined based on the capacity of the load that can be
carried or energy storage capacity. The organization of macroscopic catastrophe standards is
presented in four groups namely;
 Strain or stress failure.
 Damage failure
 Energy type failure
 Empirical failure
The criteria used in predicting the failure of the ductile material failure are normally known as
yield criteria and the frequently applied criteria of failure for materials which are ductile are;

 The extreme shear stress criterion or Tresca.
 The distortion strain energy density criterion or von Mises yield standard.
 The Garson yield criterion for pressure dependent metals.
 The Hosford yield criterion for metals.
 The Hill yield criteria
 Numerous criteria based on the invariant of the Cauchy stress tensor.
The yield surface of a ductile material usually changes as material experiences increased
deformation. Models for the evolution of the yield surface with increasing temperature, strain,
the rate of strain are used together with the above failure criteria for isotropic hardening,
viscoelasticity, and kinematic hardening (Burbank, 2011, p. 129). Estimating the final failure
strength of a ductile material is another important aspect of ductile materials. The most common
failure modes in aerospace metal alloys and polymers are the crack tip and plastic zone. A
ductile crack in a metal usually start at an existing flaw, for example, a brittle inclusion within a
grain and the stress ahead of the crack is not distributed evenly through the stress in the region
immediately ahead of the crack tip is much higher than the nominal stress (Fassi, 2017, p. 431).
The letdown of brittle material can be resolute by involving numerous approaches which include;
Phenomenological failure criteria
The type of failure criteria that were developed for brittle solids were the maximum stress/strain
criteria. The assumption made concerning maximum stress criterion is that failing in material
takes place when the maximum principal in a material element surpasses the uniaxial tensile
strength of the material. The material will fail if the minimum principal stress is less than the
uniaxial compressive strength of the material (Cummings, 2015, p. 123).

Energy based method
The mentioned above lined flexible breakage procedure technique is difficult to use for
anisotropic materials for example composites or in a situation where the geometry or loading is
complex (Revie, 2008, p. 24). The rate of a model crack is released by the strain energy that
begins over the fatness of a plate and in case the acute strain is resolute using the strain energy
release rate criteria in case the initial crack size is known (Brnic, 2018, p. 340).
Design by analysis
ASME section VIII, Boiler & Pressure Vessel (B&PV) Code provides guidelines for designing,
manufacturing, and inspection of components containing pressure. A numerical procedure
assessment is provided by the ASME guidelines to assist in developing the structural
components against local failure and plastic collapse. And design the two arts for the design and
validation of components according to ASME guidelines are the design by rules and design by
analysis (Beckmann, 2012, p. 178).
The design by analysis procedure is intended to protect against eight possible pressure vessel
failure modes by performing a detailed stress analysis of the vessel with the sufficient design
factors. The failure modes include;
 Excessive elastic deformation such as elastic instability.
 Excessive plastic deformation.
 Creep deformation/ stress rupture.
 Corrosion fatigue
 Stress corrosion
 Plastic instability.

 High strain-low cycle fatigue.
The design by analysis given in ASME relates to designs based on the elastic analysis. The
design-by-analysis requirements are organized based on protection against the failure modes
shown below. The components shall be evaluated for each applicable failure modes and only one
of the procedure mentioned below needs to be satisfied to qualify the design of a component.
a) Irrespective of pressure or size, all pressure vessels within the scope of this division shall
be protected with protection against overpressure with the requirement of this part.
b) Protection against plastic collapse.
c) Protection against local failure.
d) Protection against failure from cyclic loading.
e) Protection against collapse from bulking.

Loads and cases to be considered in a design
Loading condition Design Loads
Pressure testing Piping loads including pressure thrust
Pressure and fluids loads.
A dead load of components plus insulation
Normal operation Applicable live loads
Fluid and pressure loading during normal operations.
Dead loads of components plus insulation,
fireproofing, refractory and installed internals.
Normal operation plus occasional
(wind and earthquake usually govern
the occasional loads)
Thermal loads
Loads as a result of wave action.
Applicable live loads.
Wind, earthquake or other occasional loads
Abnormal or start-up operation plus
occasional
Wind loads
Thermal loads
Piping loads entailing pressure thrust.
Fluid and pressure loading linked with the abnormal
conditions.
Applicable live loads.

Examples of stress classification
Vessel component Location Origin of stress Type of stress
Any shell including
cylinders, cones, spheres
and formed heads.
Shell cell remote from
discontinuities.
Internal pressure
Axial thermal gradient
General membrane
Gradient through
plate thickness.
Near nozzle or other
openings.
Bending moment applied to the
nozzle or internal pressure/ net-
section axial force.
Bonding
Membrane
Any location The difference in temperature
between the head and shell
Bending
Membrane
Shell distortions such as
out of dents or roundness
Internal pressure Bending
Membrane
Conical or cylindrical
shell
Any section across the
whole vessel
Net-section axial force, bending
moments applied to the cone or
cylinder and internal pressure.
Membrane stress
averaged through
the thickness and
remote resulting
from
discontinuities.
Junction with flange or
head
Internal pressure Bending
Membrane
Conical head or Dished
head
Crown
Junction to shell or
knuckle

Underpinning
The underpinning is simply the process of strengthening the foundation of the existing structure
and building and it can be accomplished by extending the depth of the foundation.
In building or restoration, underpinning is the procedure of firming the groundwork of a
prevailing construction or additional structures (Cummings, 2015, p. 318). There is a need for
underpinning which includes the following reasons below;
 The unique groundwork is not firm or robust enough.
 The change in usage of the construction.
 The features of the soil holding the foundations may have altered maybe as a result
of subsidence (Roters, 2007, p. 410).
 The construction of nearby structures necessitates the excavation of soil supporting
existing foundations.
 To upsurge the depth or load capacity of existing foundations to support the
addition of another store to the building.
 It is economical due to the price of land or to work on the foundation of the present
structure than building a new one.
 Earthquake, drought, flood or other natural causes have caused the structure to
move, requiring stabilization of foundation soils or footings.
Underpinning may be accomplished by extending the foundation in depth or breadth so it is
either rests on a more supportive soil distributes or stratum its load across a greater area. In
underpinning, most methods used are the jet grouting and the micro piles (Broek, 2013, p. 239).

Mass Concrete Underpinning is underpinning method which was used for almost 100 years and
it reinforces a prevailing erections groundwork through excavating boxes using hand beneath and
successively hammering solid in a planned order. The outcome of the groundwork constructed
beneath the current foundation falling at low depth but works well up to fifty feet deep. This type
of method does not employ heavy machinery, as a result, the small size of the boxes that are
excavated and this method has numerous advantages, for example, low labor cost, the simplicity
of the engineering and the continuity of the structures used during the construction (Bower,
2009, p. 459).
The beam and base method of underpinning is further precisely progressive adaption of the
outdated approach of the foundation. A protected concrete beam is erected beneath, overhead or
in spare of the prevailing footing (Kuna, 2013, p. 97). The building load is transferred to mass
concrete bases whose constructions take place in intended strategic locations. The base depth and
sizes are reliant on upon the confirmation of the structure and the loads applied (Black, 2015, p.
123)
The use of mini-piles takes place where the ground conditions are variable and accessing them is
restricted and in a situation where pollution of environmental features are important and where
physical movement in service must be minimal (Noon, 2008, p. 567). This type of underpinning
method known as mini-pile is usually used in a situation where weights from the bases demand
to be transferred to the soil which is stable at a considerable depth and normally excess of 5m
(Besson, 2009, p. 761).
The rigs are used by the engineers designed normally to work in surroundings having limited
space and headroom and can get entrée via a steady domestic doorway. They are in a position of
piles construction to a depth amounting to 15m and this type of technique of mini piling was first

applied in Italy in 1952, commonly apply tiebacks or anchoring into existing structure an
existing rock or structure (Goodwall, 2009, p. 128). For this method of underpinning, grouting
and conventional drilling methods are used and they have a high slenderness ratio thus sustaining
axial loading in both senses can be done.
The mini piles are made so that they can be applied in compression and tension depending on the
application and orientation of the design and when designing it, much concentration must be
based on cracking, bursting, interface consideration and buckling whereby the opposing
oxidization and compatibility with the prevailing earth and structure must be viewed (Beckmann,
2012, p. 123).
Mini-piled underpinning schemes involve mini-piled understanding structures comprise beam
and pile, plank pile-caps and piled raft schemes (Kohser, 2013, p. 721). Evading upsetting the
inner side of a structure, planked pile-caps are normally applied and needs the building of tension
and compression piles to every cap. The system of pile and beam normally entails building pile
pairs on both wall side and connecting a pile cap to sustenance the wall (Agawai, 2017, p. 134).
The linking of the pile caps is normally done using the protected solid beams to assist in
supporting the whole dimension of the wall and the usage of pile raft underpinning system takes
place in a situation where the whole of the building require underpinning. The internal floors
found internally are removed completely, installation of piles grid and a construction of a
strengthened tangible raft over the whole floor level and back up the internal and external walls
fully (Askeland, 2015, p. 78).

Bibliography
Agawam, B., 2017. Analysis and Performance of Fiber Composite. s.l. Cambridge University Press.
Askeland, D., 2015. Constitutive Laws of Plastic Deformation and Structure. s.l. Gakken.
Beckmann, P., 2012. Structural Aspect of Building Conservation. s.l. Haufe Grupe.
Besson, J., 2009. Local Approach To Fracture. s.l. Weka.
Black, B., 2015. Workshop Processes, Practices, and Materials. s.l. Cambridge University Press.
Bower, A., 2009. Applied Mechanics of Solids. s.l.: Hachette Livre.
Brnic, J., 2018. Analysis of Engineering Structure and Material Behavior. s.l. Sanoma.
Broek, I., 2013. The Practical Use of Fracture Mechanics. s.l.: Wiley.
Burbank, D., 2011. Tectonic Geomorphology. s.l.: Reed Elsevier.
Burr, D., 2013. Basics and Applied Bone Biology. s.l. OLMA Media Group.
Byfield, M., 2018. Structural Design From First Principles. : Sanoma.
Chirag, P., 2015. Repair and Rehabilitation of Concrete Structures. s.l. Scholastic.
Collins, J., 2014. Failure of Material in Mechanical Design and Analysis. s.l.: Random House.
Courtney, T., 2008. Mechanical Behavior of Material. s.l. Gakken.
Cummings, R., 2015. Applied Computational Aerodynamics. s.l.: Wolters Kluwer.
Dieter, G., 2014. Mechanical Metallurgy. s.l.:Media Participations.
Fassi, I., 2017. Micro-Manufacturing Technologies and Their Application. s.l. Weka.
Goh, K.-L., 2016. Discountinuous-Fibre Reinforced Composites. s.l.:Grupo Santilla.
Goodwill, I., 2009. Reference Stress Methods. s.l.: Pearson.
Gupta, K., 2017. Advance Manufacturing Technologies. s.l.: Gakken.
Hertzberg, T., 2012. Deformation and Fracture Mechanics of Engineering Material. s.l. Media
Participations.
Hiermairer, S., 2007. Structure Under Crash and Impact. s.l.: Random House.
Holdsworth, S., 2008. Creep and Fracture in High-Temperature Components. s.l.: Wolters Kluwer.
Kohser, P., 2013. Materials and Processes in Manufacturing. s.l.: Pearson.
Kotelyanskii, M., 2008. Simulation Methods for Polymers. s.l. Media Participations.
Kuna, M., 2013. Finite Elements in Fracture Mechanics. s.l.:Informa.
Li, S., 2008. Introduction to Micromechanics and Nanomechanics. s.l.:Simon & Schuster.

Littlejohn, T., 2011. Underpinning and Retention. s.l.: Wiley.
Li, Y., 2007. Ductile fracture due to Plastic flow, void growth, and localization. s.l.: China Publishing
Company.
Mai, A., 2009. Nonlinear fracture and damage mechanics. s.l.: Random House.
Moavenzadeh, F., 2016. Concise Encyclopedia of Building and Construction Material. s.l.: Wolters Kluwer.
Noon, R., 2008. Forensic Engineering Investigation. s.l. Sanoma.
Pullan, W., 2007. Structure in Science and Art. s.l. Adventure Works Press.
Reginald, F., 2010. Theory of Crystal Dislocations. s.l. Adventure Works press.
Review, W., 2008. Corrosion and Corrosion Control. s.l.: China Publishing Company.
Rogers, F., 2007. Continuum Scale Simulations of Engineering Materials. s.l. Editions Atlas.
Sammy, H., 2009. A Quick Guide to Welding and Weld Inspection. s.l.: Readers Digest.
Tomlinson, M., 2014. Pile Design and Construction Practices. s.l.:Informa.
Wadsworth, S., 2009. Superplasticity in Metals and Ceramics. s.l. Editions Atlas.
Williams, D., 2014. Essentials Biomaterials in Science. s.l.: Readers Digest.
Woodward, J., 2017. Atomistic Origins of Ductility Enhancement in Metal Oxide. s.l. Scholastic.