SPSS Data Analysis for Annual Rainfall, Daily Maximum Rainfall, and Monthly Maximum Rainfall

This study applies data analysis skills using SPSS software for annual rainfall, daily maximum rainfall, and monthly maximum rainfall. The methodology, results, and discussion of the analysis are presented. Descriptive analysis, data recoding, chi-square test, t-test, and ANOVA are performed. The dataset is explored and its distribution is analyzed.

Assignment 1: Tutorial Questions
CIVE 5015
Research Data Analysis
SP2 2018
University of Australia
Dataset:
Annual rainfall, Annual daily maximum rainfall, Annual monthly maximum rainfall
Name:
Student ID:
1

Table of Contents
1. Introduction..............................................................................................................................4
2. SPSS version 25 data analysis..................................................................................................4
2.1 Task 1: Descriptive analysis.............................................................................................4
2.1.1 Methodology..............................................................................................................5
2.1.2 Results........................................................................................................................6
2.1.2.1 Descriptive analysis...................................................................................................6
2.1.2.2 Histogram for annual rainfall (AR) with Distribution Curve....................................7
2.1.2.3 Histogram for annual daily maximum rainfall (ADMR) with Distribution Curve. . .7
2.1.2.4 Histogram for annual monthly maximum rainfall (AMMR) with Distribution Curve
8
2.1.2.5 Boxplots.....................................................................................................................8
2.1.3 Discussion..................................................................................................................8
2.2 Task 2: Data Recoding......................................................................................................9
2.2.2 Results......................................................................................................................10
2.2.2.1 Data Analysis...........................................................................................................10
2.2.2.2 Data recoding...........................................................................................................10
2.2.3 Summary..................................................................................................................11
2.3 Task 3: Chi square Test...................................................................................................11
2.3.2 Results......................................................................................................................11
2

2.3.2.1 Establish Chi Square Test Hypothesis.....................................................................11
2.3.2.2 Chi-Square output....................................................................................................12
2.3.3 Discussion................................................................................................................13
2.4 Task 4: T-test..................................................................................................................13
2.4.1 Methodology............................................................................................................14
2.4.2 Results......................................................................................................................14
2.4.2.1 Establish T- Test Hypothesis...................................................................................14
2.4.2.2 T-test output.............................................................................................................15
2.4.3 Discussion................................................................................................................15
2.5 Task 5: ANOVA.............................................................................................................16
2.5.1 Methodology............................................................................................................16
2.5.2 Results......................................................................................................................16
2.5.2.1 Establish ANOVA Test Hypothesis........................................................................16
2.5.2.2 ANOVA output........................................................................................................17
2.5.3 Discussion................................................................................................................18
3. Conclusion..............................................................................................................................18
References......................................................................................................................................19
Appendixes....................................................................................................................................20
3

1. Introduction
This study is applying the data analysis skills which is a component of the research. The IBM
Statistical Software for Social Sciences (SPSS) is used to perform the required analysis of the
given data set. According to Levesque (2007), SPSS is a powerful software that can be used to
perform various analysis ranging from comparing of means to reliability testing among many
others. The software has syntax part and the point and click sections where people can use to
perform various analysis. It is easy to use and very friendly to even non-statisticians. This study
utilized the dataset on Annual rainfall (AR), Annual daily maximum rainfall (ADMR), Annual
monthly maximum rainfall (AMMR). The aim of the study is to demonstrate the data analysis
skills and apply them on real life events.
2. SPSS version 25 data analysis
This section is divided into 5 different subsections that explains the utilization of different SPSS
techniques to perform analysis. Data for this study was collected from the following website
www.bom.gov.au. The next sections outlines the step-by-step used to perform the various
analysis. The SPSS output and results have also been provided along with the interpretation of
the various results. The preliminary analysis which tries to explore the dataset is the first
subsection. Other analysis techniques discussed in this report include the Chi-square test of
association, t-test for comparing means of two factors, analysis of variance (ANOVA) for
comparing means of more than 2 factors.
2.1 Task 1: Descriptive analysis
Descriptive analysis which also includes frequency analysis is the most commonly used analysis
for exploring the dataset before performing any inferential analysis. The analysis captures the
4

mean, mode and median of the data set commonly known as the measures of central tendency.
Other measures include the standard deviation which is a measure of variation. To check for
distribution of data, kurtosis and skewness was used.
2.1.1 Methodology
This section presents the methodology used from data collection to presentation of the analyzed
data set.
5
1. Data collection
Computing the rainfall data into Microsoft Excel documents
Access Bom website > Select the station > Download the data sets > Tabulate the data
into Microsoft Excel
2. Data entries
Extract water consumption data to the SPSS software. Once the data has been extracted
into the software, configure the variables to scale measure.
Extract Excel water consumption data into SPSS variable name > Change the name
and the scale measure for the variable.
3. SPSS function: Descriptive Analysis
The next step is to perform the descriptive analysis for the three variables. The analysis
seeks to produce the mean, median and mode.
Open SPSS file > Analyze > Descriptive Statistics > Frequencies & Descriptive

2.1.2 Results
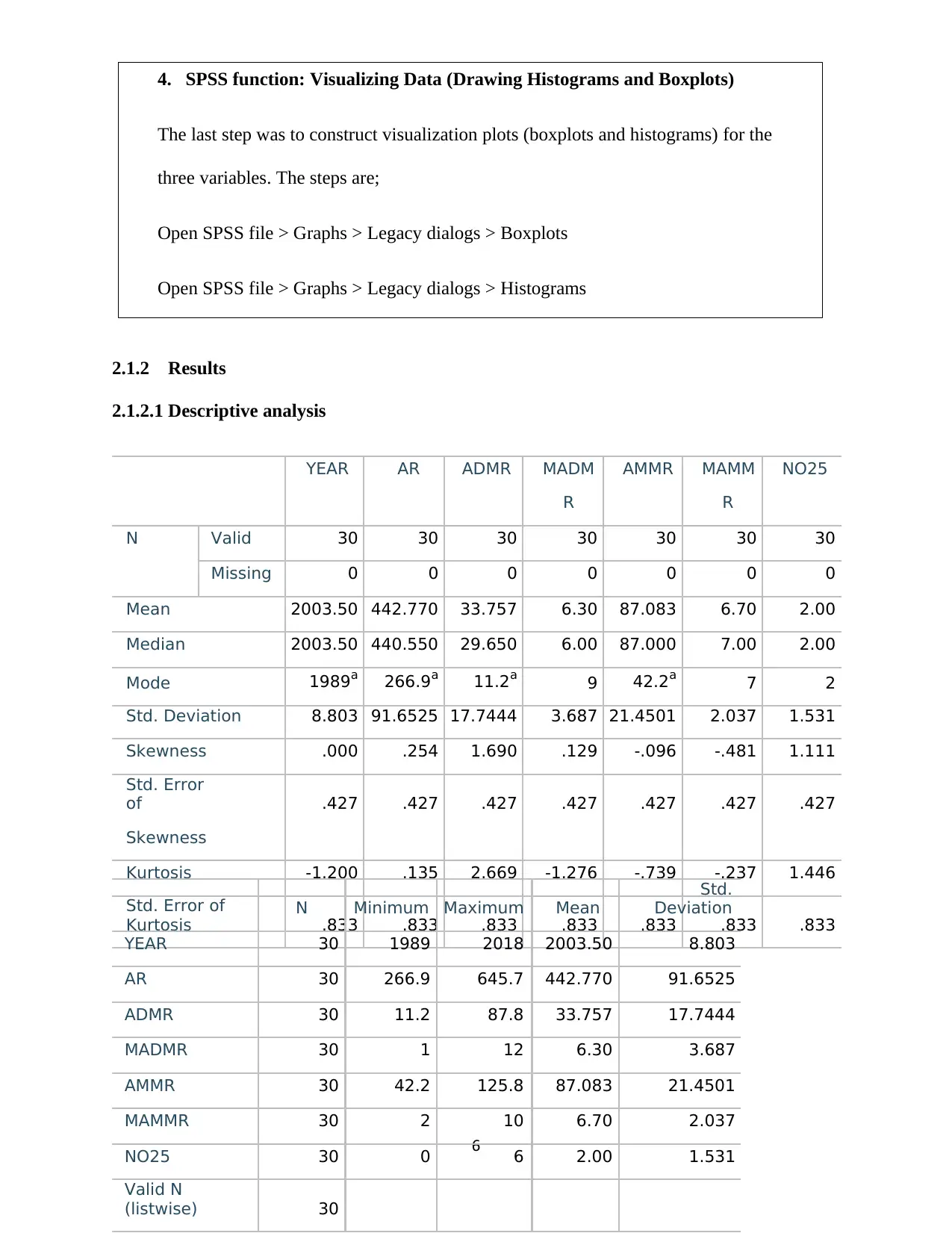
2.1.2.1 Descriptive analysis
YEAR AR ADMR MADM AMMR MAMM NO25
R R
N Valid 30 30 30 30 30 30 30
Missing 0 0 0 0 0 0 0
Mean 2003.50 442.770 33.757 6.30 87.083 6.70 2.00
Median 2003.50 440.550 29.650 6.00 87.000 7.00 2.00
Mode 1989a 266.9a 11.2a 9 42.2a 7 2
Std. Deviation 8.803 91.6525 17.7444 3.687 21.4501 2.037 1.531
Skewness .000 .254 1.690 .129 -.096 -.481 1.111
Std. Error
of .427 .427 .427 .427 .427 .427 .427
Skewness
Kurtosis -1.200 .135 2.669 -1.276 -.739 -.237 1.446
Std. Error of
Kurtosis .833 .833 .833 .833 .833 .833 .833
6
4. SPSS function: Visualizing Data (Drawing Histograms and Boxplots)
The last step was to construct visualization plots (boxplots and histograms) for the
three variables. The steps are;
Open SPSS file > Graphs > Legacy dialogs > Boxplots
Open SPSS file > Graphs > Legacy dialogs > Histograms
N Minimum Maximum Mean
Std.
Deviation
YEAR 30 1989 2018 2003.50 8.803
AR 30 266.9 645.7 442.770 91.6525
ADMR 30 11.2 87.8 33.757 17.7444
MADMR 30 1 12 6.30 3.687
AMMR 30 42.2 125.8 87.083 21.4501
MAMMR 30 2 10 6.70 2.037
NO25 30 0 6 2.00 1.531
Valid N
(listwise) 30

2.1.2.2 Histogram for annual rainfall (AR) with Distribution Curve
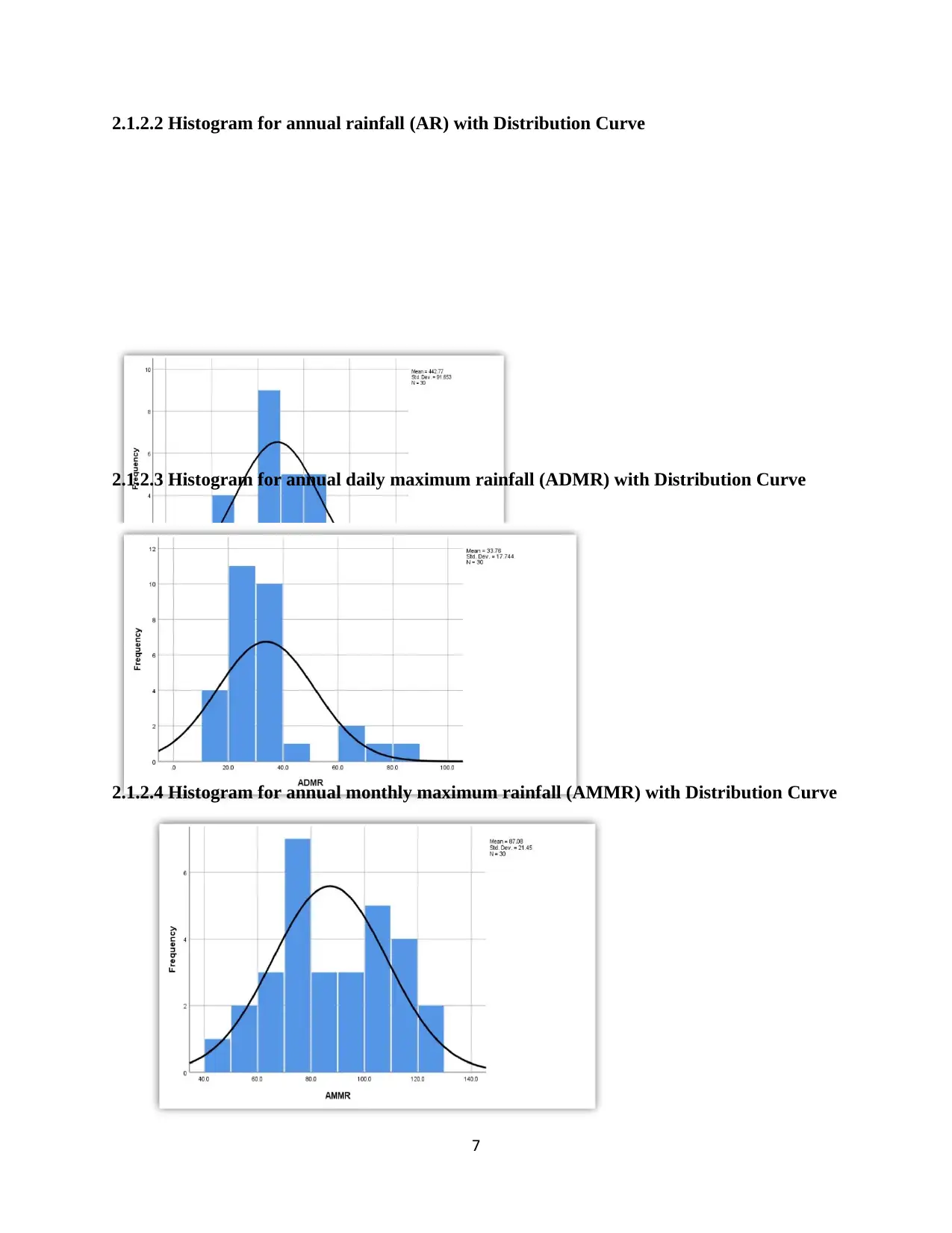
2.1.2.3 Histogram for annual daily maximum rainfall (ADMR) with Distribution Curve
2.1.2.4 Histogram for annual monthly maximum rainfall (AMMR) with Distribution Curve
7

2.1.2.5 Boxplots
2.1.3 Discussion
Sections 2.1.2.1 – 2.1.2.5 presents the results of the descriptive analysis as well as the plots for
the different variables (annual rainfall, annual daily maximum rainfall and the annual monthly
maximum rainfall). As can be seen from the table, annual rainfall had the highest mean (M =
442.77, SD = 91.65) while annual daily maximum rainfall had the lowest mean (M = 33.76, SD
= 17.74). The annual monthly maximum rainfall had an average of 87.08 (SD = 21.45). In terms
of skewness, annual monthly maximum rainfall was the least skewed (skewness = -.096) while
annual daily maximum rainfall (ADMR) had the highest skewness value (skewness = 1.690).
The values further shows that the data for annual monthly maximum rainfall (AMMR) and
annual rainfall were found to be close to normal distribution while that of annual daily maximum
rainfall is highly positively skewed.
8

The histograms further confirms the distributions where we can see that the distribution for the
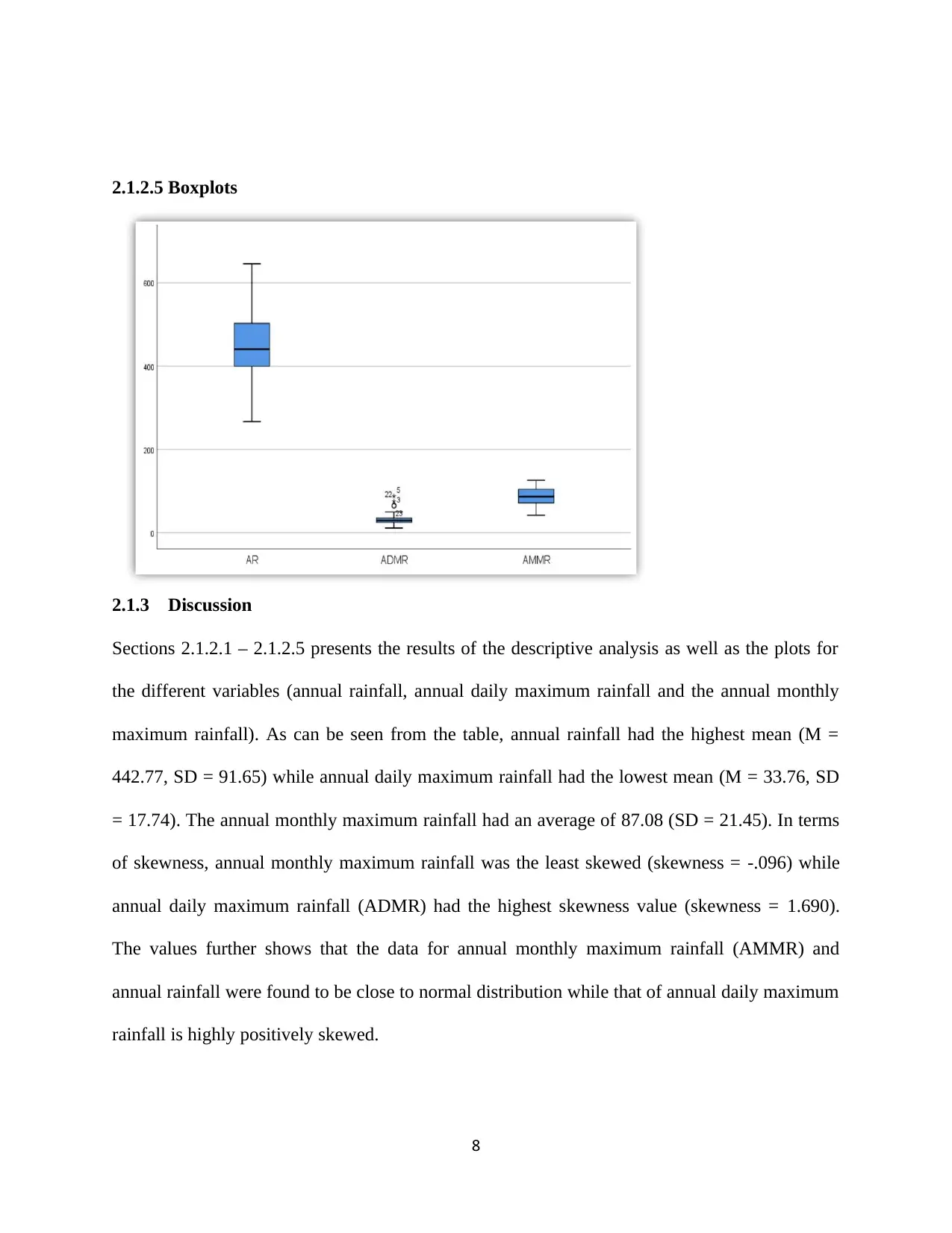
annual daily maximum rainfall to be highly positively skewed (having a longer tail to the right).
The boxplots shows that there are outliers for the annual daily maximum rainfall dataset while
the two other datasets don’t have outliers. The presence of outliers in the annual daily maximum
rainfall could possibly explain why it was heavily skewed.
2.2 Task 2: Data Recoding
Data recording for both the mining and manufacturing were re-coded in order to generate
categorical variables. Recoding is crucial especially when it comes to performing a Chi-square
test of association.
2.2.1 Methodology
The following steps were followed in order to recode the data.
9
1. Data recoding
We sought to transform the existing data into 4 new groups
2. SPSS function: Recoding codes
We sought to transform the existing data into 4 new groups. The codes are given
below;
3. SPSS function: Frequency Analysis
Frequency analysis was performed as follows;
Open SPSS file > Analyze > Descriptive Statistics > Frequencies
4. SPSS function: Bar charts
Frequency analysis was performed as follows;
Open SPSS file > Analyze > Descriptive Statistics > Frequencies> Select charts > Bar
charts

2.2.2 Results
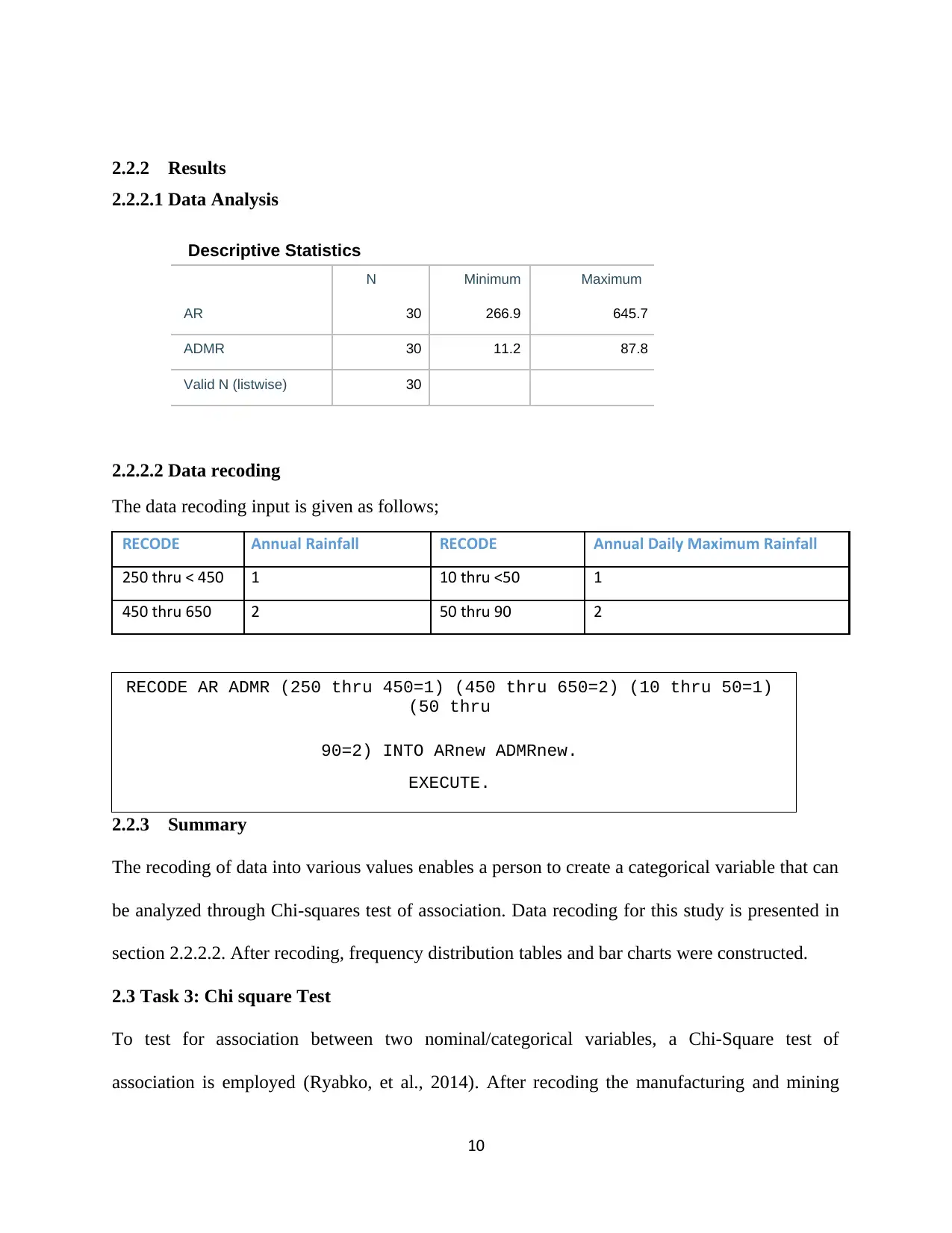
2.2.2.1 Data Analysis
Descriptive Statistics
2.2.2.2 Data recoding
The data recoding input is given as follows;
RECODE Annual Rainfall RECODE Annual Daily Maximum Rainfall
250 thru < 450 1 10 thru <50 1
450 thru 650 2 50 thru 90 2
2.2.3 Summary
The recoding of data into various values enables a person to create a categorical variable that can
be analyzed through Chi-squares test of association. Data recoding for this study is presented in
section 2.2.2.2. After recoding, frequency distribution tables and bar charts were constructed.
2.3 Task 3: Chi square Test
To test for association between two nominal/categorical variables, a Chi-Square test of
association is employed (Ryabko, et al., 2014). After recoding the manufacturing and mining
10
RECODE AR ADMR (250 thru 450=1) (450 thru 650=2) (10 thru 50=1)
(50 thru
90=2) INTO ARnew ADMRnew.
EXECUTE.
N Minimum Maximum
AR 30 266.9 645.7
ADMR 30 11.2 87.8
Valid N (listwise) 30

data we were able to have categorical variables. In the next section, we present the methodology
that was used to run the chi-square test for this study.
2.3.1 Methodology
2.3.2 Results
2.3.2.1 Establish Chi Square Test Hypothesis
Null hypothesis (H0): There is no significant association between annual rainfall and annual daily
maximum rainfall.
Alternative hypothesis (HA): There is significant association between annual rainfall and annual
daily maximum rainfall
2.3.2.2 Chi-Square output
Cases
Valid Missing Total
N Percent N Percent N Percent
ARnew * ADMRnew 30 100.0% 0 0.0% 30 100.0%
11
1. Establish a hypothesis to be tested
The following hypothesis was to be tested for this study;
Null hypothesis (H0): There is no significant association between annual rainfall and
annual daily maximum rainfall.
Alternative hypothesis (HA): There is significant association between annual rainfall
and annual daily maximum rainfall.
2. Perform Chi-square Test: Hypothesis Testing
The procedure for a chi-square test is as follows;
Analyze > Descriptive Statistics > Cross tabs > Data input in rows and columns >
Statistics > Chi-square > Phi and Cramer’s V

Case Processing Summary
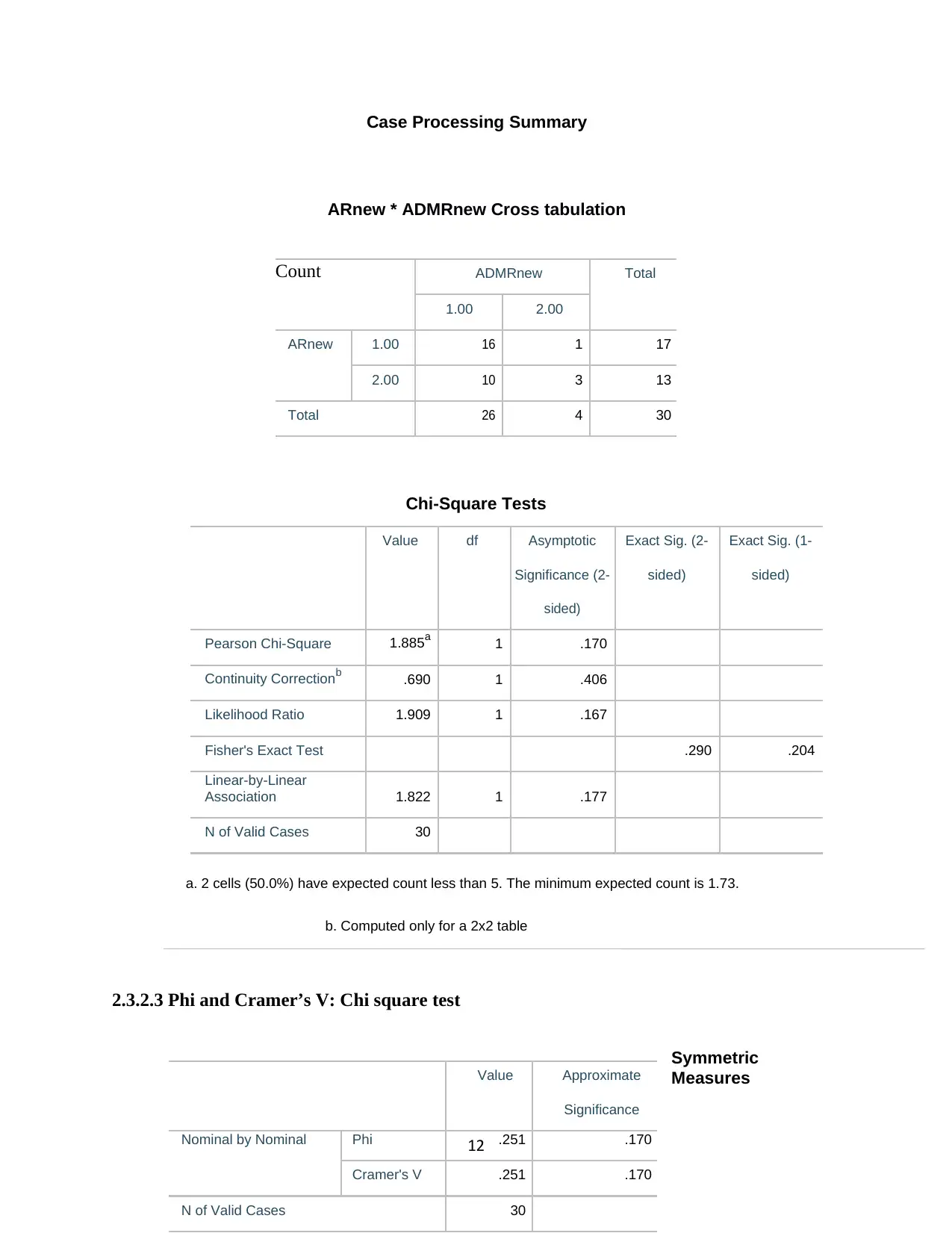
ARnew * ADMRnew Cross tabulation
Chi-Square Tests
Value df Asymptotic Exact Sig. (2- Exact Sig. (1-
Significance (2- sided) sided)
sided)
Pearson Chi-Square 1.885a 1 .170
Continuity Correctionb .690 1 .406
Likelihood Ratio 1.909 1 .167
Fisher's Exact Test .290 .204
Linear-by-Linear
Association 1.822 1 .177
N of Valid Cases 30
a. 2 cells (50.0%) have expected count less than 5. The minimum expected count is 1.73.
b. Computed only for a 2x2 table
2.3.2.3 Phi and Cramer’s V: Chi square test
Symmetric
Measures
12
Count ADMRnew Total
1.00 2.00
ARnew 1.00 16 1 17
2.00 10 3 13
Total 26 4 30
Value Approximate
Significance
Nominal by Nominal Phi .251 .170
Cramer's V .251 .170
N of Valid Cases 30

2.3.3 Discussion
The p-value for the Chi-square test is given as 0.170 (a value greater than 5% level of
significance), we therefore fail to reject the null hypothesis and conclude that there is no
significant association between annual rainfall and annual daily maximum rainfall. The Phi and
the Cramer’s V further show that the association between the two variables is very weak hence
no association between the two variables.
2.4 Task 4: T-test
T-test is normally performed to compare the difference in the means of two unrelated groups
(Fay & Proschan, 2010). A case where we have more than two groups then ANOVA comes to
play. SPSS offers a good platform to perform t-test. For this study, we sought to determine
whether there is significant difference in the mean annual rainfall for the group data of the annual
daily (Sawilowsky, 2005). In the next sections, we present the methodology for performing the t-
test for this study.
2.4.1 Methodology
13
1. Data Preparation : Categorize independent Variable
Independent variable = annual daily maximum rainfall (group data)
Dependent variable = annual daily maximum rainfall (mm)
Divide daily maximum rainfall data into 2 group→ (1= equal or less than 50mm
and 2=greater than 50mm)

2.4.2 Results
2.4.2.1 Establish T- Test Hypothesis
Null hypothesis (H0): There is no significant difference in the mean annual daily maximum
rainfall for the two groups.
Alternative hypothesis (HA): There is significant difference in the mean annual daily
maximum rainfall for the two groups.
2.4.2.2 T-test output
Group Statistics
GRFt N Mean Std. Deviation
Std. Error
Mean
ADMR 1 16 27.312 14.3698 3.5924
2 14 41.121 18.8310 5.0328
Levene's Test for
t-test for
Equality of
Means
14
2. Establish a hypothesis to be tested
The following hypothesis was to be tested for this study;
Null hypothesis (H0): There is no significant difference in the mean annual daily
maximum rainfall for the two groups.
Alternative hypothesis (HA): There is significant difference in the mean annual daily
maximum rainfall for the two groups
3. Perform Chi-square Test: Hypothesis Testing
The procedure for a chi-square test is as follows;
Analyze > Compare means > Independent-samples t-test > Test variable: dependent
variable (annual daily maximum rainfall) > Grouping variable: independent variable
(rainfall grouped group) → Define groups (1, 2)

Equality of
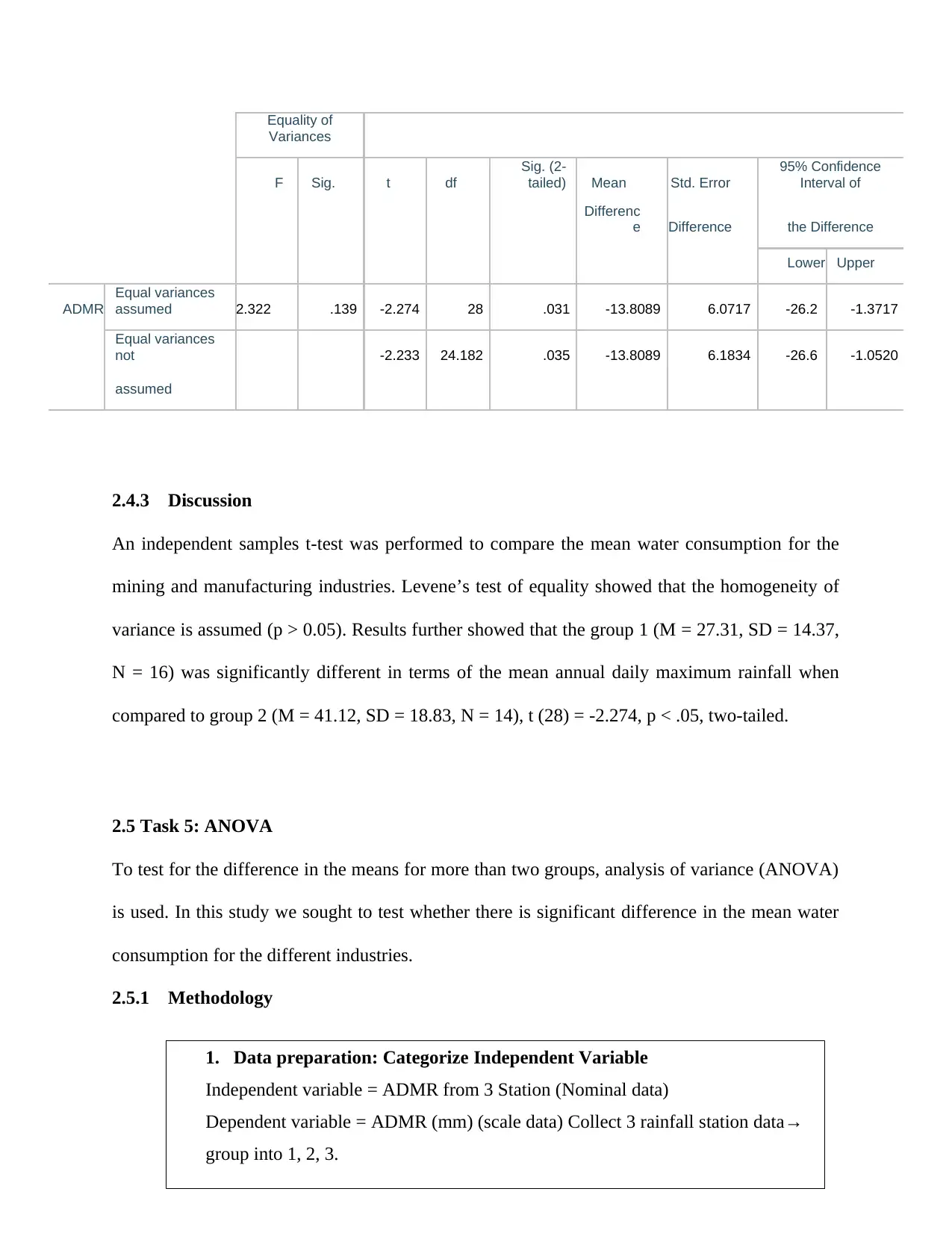
Variances
F Sig. t df
Sig. (2-
tailed) Mean Std. Error
95% Confidence
Interval of
Differenc
e Difference the Difference
Lower Upper
ADMR
Equal variances
assumed 2.322 .139 -2.274 28 .031 -13.8089 6.0717 -26.2 -1.3717
Equal variances
not -2.233 24.182 .035 -13.8089 6.1834 -26.6 -1.0520
assumed
2.4.3 Discussion
An independent samples t-test was performed to compare the mean water consumption for the
mining and manufacturing industries. Levene’s test of equality showed that the homogeneity of
variance is assumed (p > 0.05). Results further showed that the group 1 (M = 27.31, SD = 14.37,
N = 16) was significantly different in terms of the mean annual daily maximum rainfall when
compared to group 2 (M = 41.12, SD = 18.83, N = 14), t (28) = -2.274, p < .05, two-tailed.
2.5 Task 5: ANOVA
To test for the difference in the means for more than two groups, analysis of variance (ANOVA)
is used. In this study we sought to test whether there is significant difference in the mean water
consumption for the different industries.
2.5.1 Methodology
15
1. Data preparation: Categorize Independent Variable
Independent variable = ADMR from 3 Station (Nominal data)
Dependent variable = ADMR (mm) (scale data) Collect 3 rainfall station data→
group into 1, 2, 3.

2.5.2 Results
2.5.2.1 Establish ANOVA Test Hypothesis
Null hypothesis (H0): There is no significant difference in the mean annual daily maximum
rainfall for the three groups.
Alternative hypothesis (HA): At least one of the group is different.
2.5.2.2 ANOVA output
ANOVA
ADMR
Sum of df Mean Square F Sig.
Squares
Between Groups 368.645 2 184.322 .713 .493
Within Groups 23013.525 89 258.579
16
2. Establish a hypothesis to be tested
The following hypothesis was to be tested for this study;
Null hypothesis (H0): There is no significant difference in the mean annual daily
maximum rainfall for the three groups.
Alternative hypothesis (HA): At least one of the group is different.
3. Perform Chi-square Test: Hypothesis Testing
The procedure for a chi-square test is as follows;
Analyze > Compare means > One-way ANOVA > Dependent list (annual daily
maximum rainfall) → Factor (independent variable; ADMR group)

Total 23382.170 91
Report
ADMR
Station Mean N Std. Deviation
1 33.757 30 17.7444
2 37.155 31 13.3726
3 32.423 31 16.8500
Total 34.452 92 16.0296
2.5.2.3 Testing for magnitude difference
ANOVA
Sum of df Mean Square F Sig.
Squares
Between Groups 368.645 2 184.322 .713 .493
Within Groups 23013.525 89 258.579
Total 23382.170 91
2.5.2.4 Eta values (strength of association)
Eta Eta Squared
ADMR * Station .126 .016
2.5.3 Discussion
The p-value for the ANOVA test was found to be 0.493 (a value greater than 5% level of
significance), we therefore fail to reject the null hypothesis and conclude that there is no
17

significant difference in the mean annual daily maximum rainfall for the three groups. Eta value
also showed that the association is very low.
3. Conclusion
The aim of this study was to try and analyze rainfall data. Chi-square test of association showed
a significant association between the mining and manufacturing industries. There was however,
no significant difference in the mean water consumption for the manufacturing and mining based
on the t-test. ANOVA test was also significant showing difference in water consumption for the
mining and aquaculture industries.
SPSS
hypothesis test
Testing value
α = 0.05
Results Remarks
Chi-Square test p-value .170 Fail to reject the null
hypothesis
There is no association
between the variables
t-test p-value .031 Reject the null hypothesis There is significant
difference in the two groups
ANOVA p-value .493 Fail to reject the null
hypothesis
There is no difference in the
mean for the three groups
References
Anscombe, F. J., 2015. The Validity of Comparative Experiments. Journal of the Royal
Statistical Society, 11(3), p. 181–211.
Fay, M. P. & Proschan, M. A., 2010. Wilcoxon–Mann–Whitney or t-test? On assumptions for
hypothesis tests and multiple interpretations of decision rules. Statistics Surveys, 4(3), p. 1–39.
18

Gelman, A., 2012. Analysis of variance? Why it is more important than ever. The Annals of
Statistics, Volume 33, p. 1–53.
Levesque, R., 2007. SPSS Programming and Data Management: A Guide for SPSS and SAS
Users (4th ed.). Chicago, Illinois: SPSS Inc..
Ryabko, B. y., Stognienko, V. S. & Shokin, Y. I., 2014. A new test for randomness and its
application to some cryptographic problems. Journal of Statistical Planning and Inference,
Volume 123, p. 365–376.
Sawilowsky, S. S., 2005. Misconceptions Leading to Choosing the t Test Over The Wilcoxon
Mann–Whitney Test for Shift in Location Parameter. Journal of Modern Applied Statistical
Methods, 4(2), p. 598–600.
Appendixes
Climate data
Climate data of annual rainfall, annual daily maximum rainfall of Adelaide (pooraka) 023026 climate
station. Collected from http://www.bom.gov.au/climate/data/?ref=ftr
19