Signals and Systems Homework: MATLAB Analysis and Solutions
VerifiedAdded on 2022/09/29
|9
|1002
|19
Homework Assignment
AI Summary
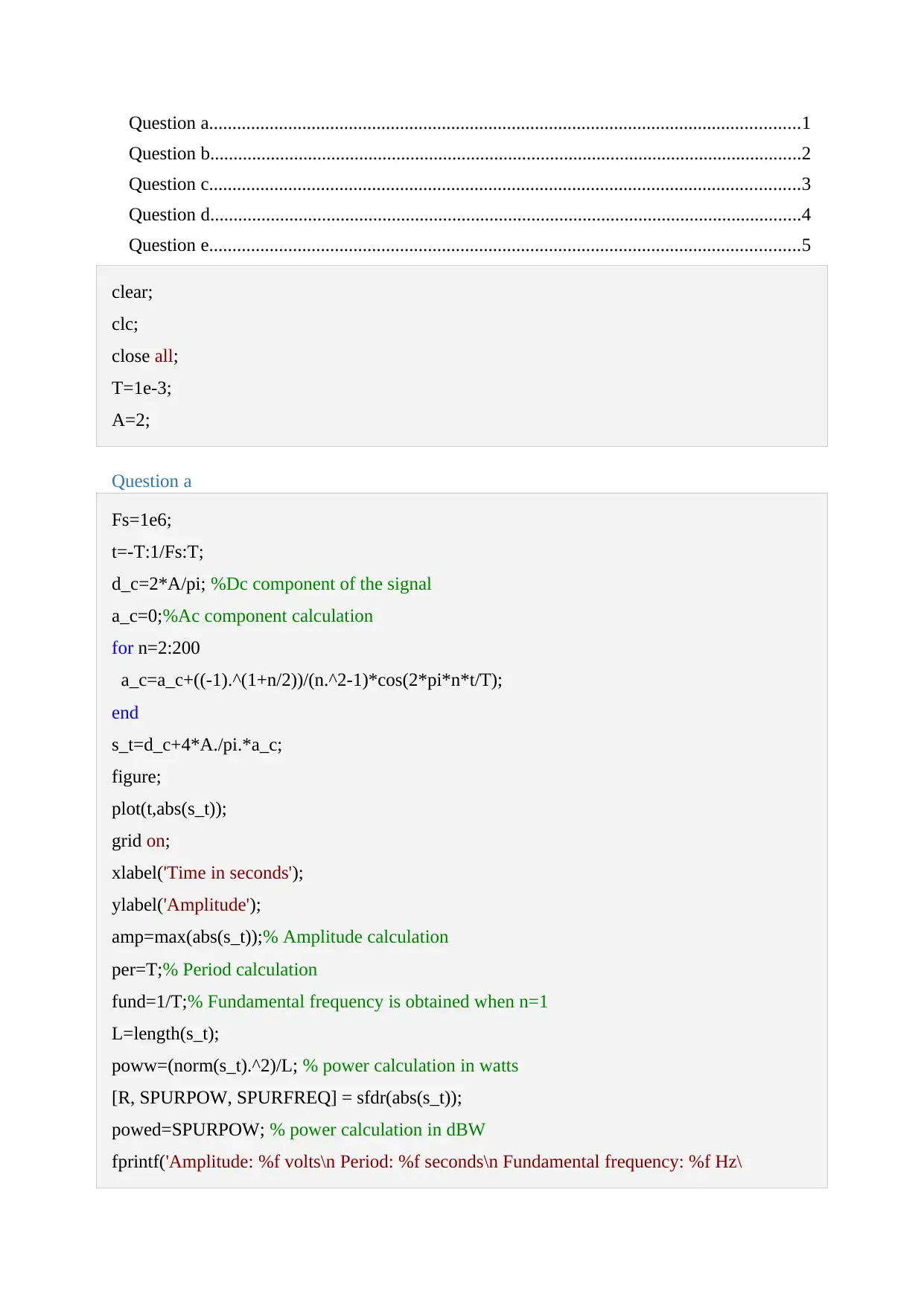
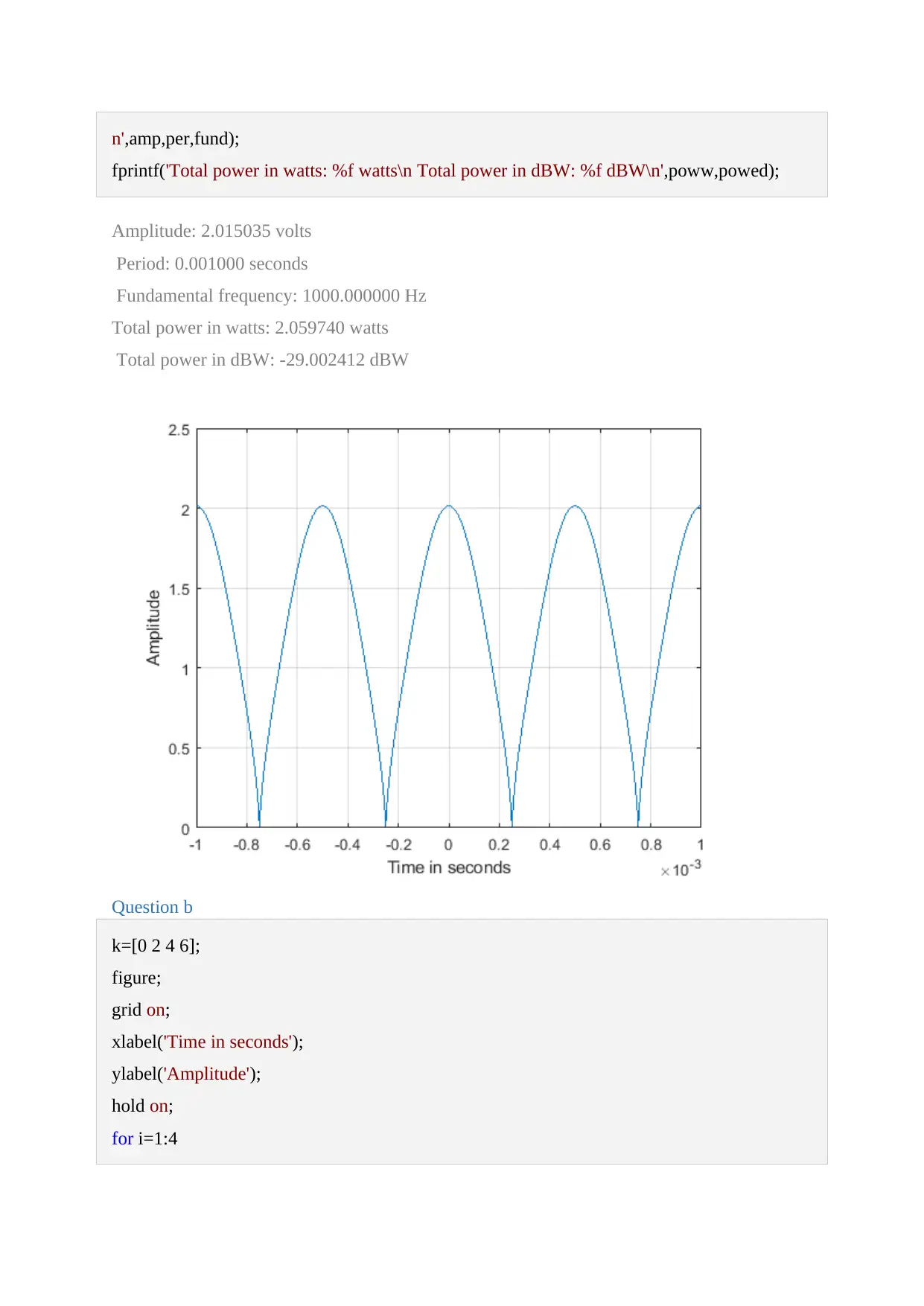
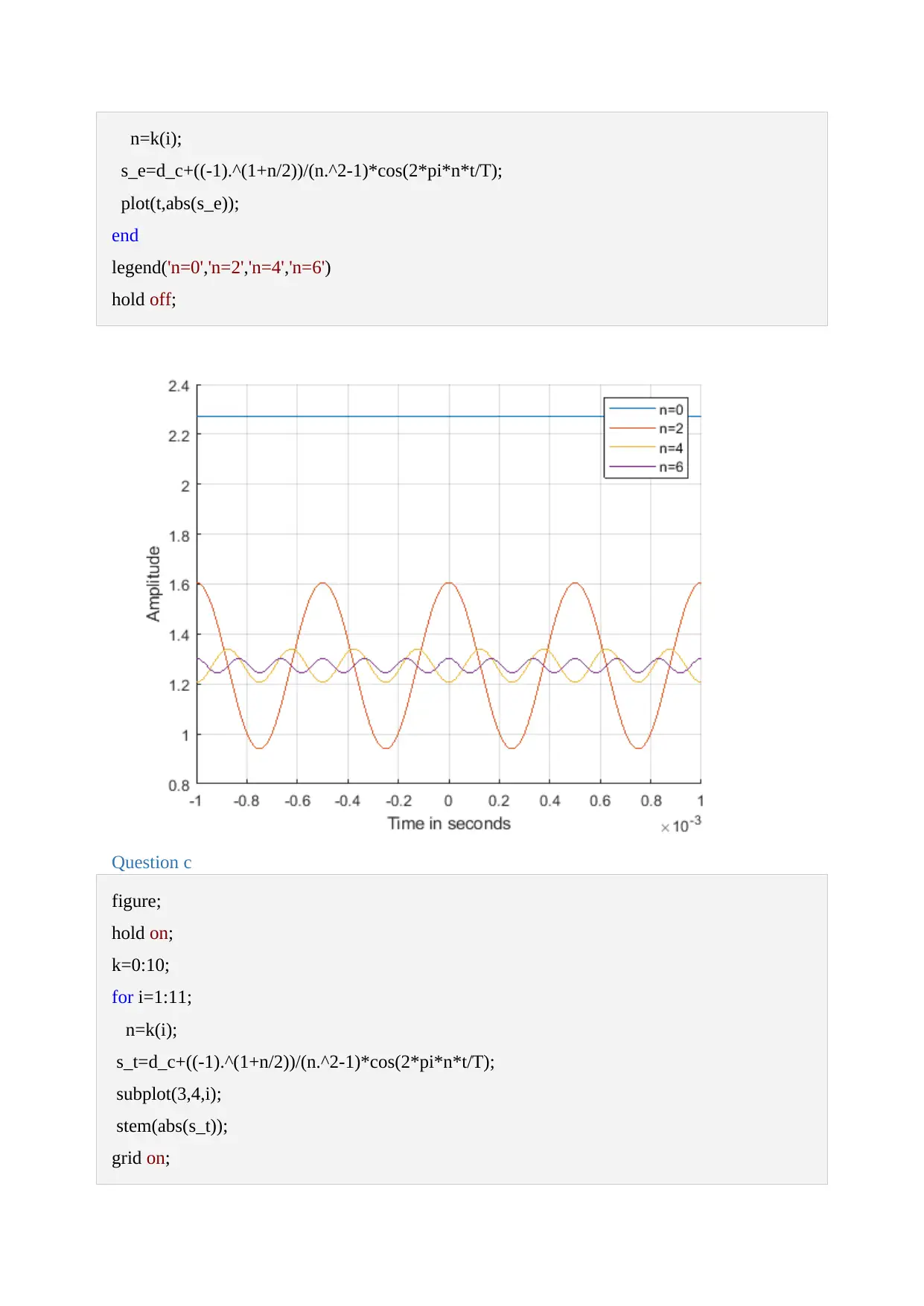
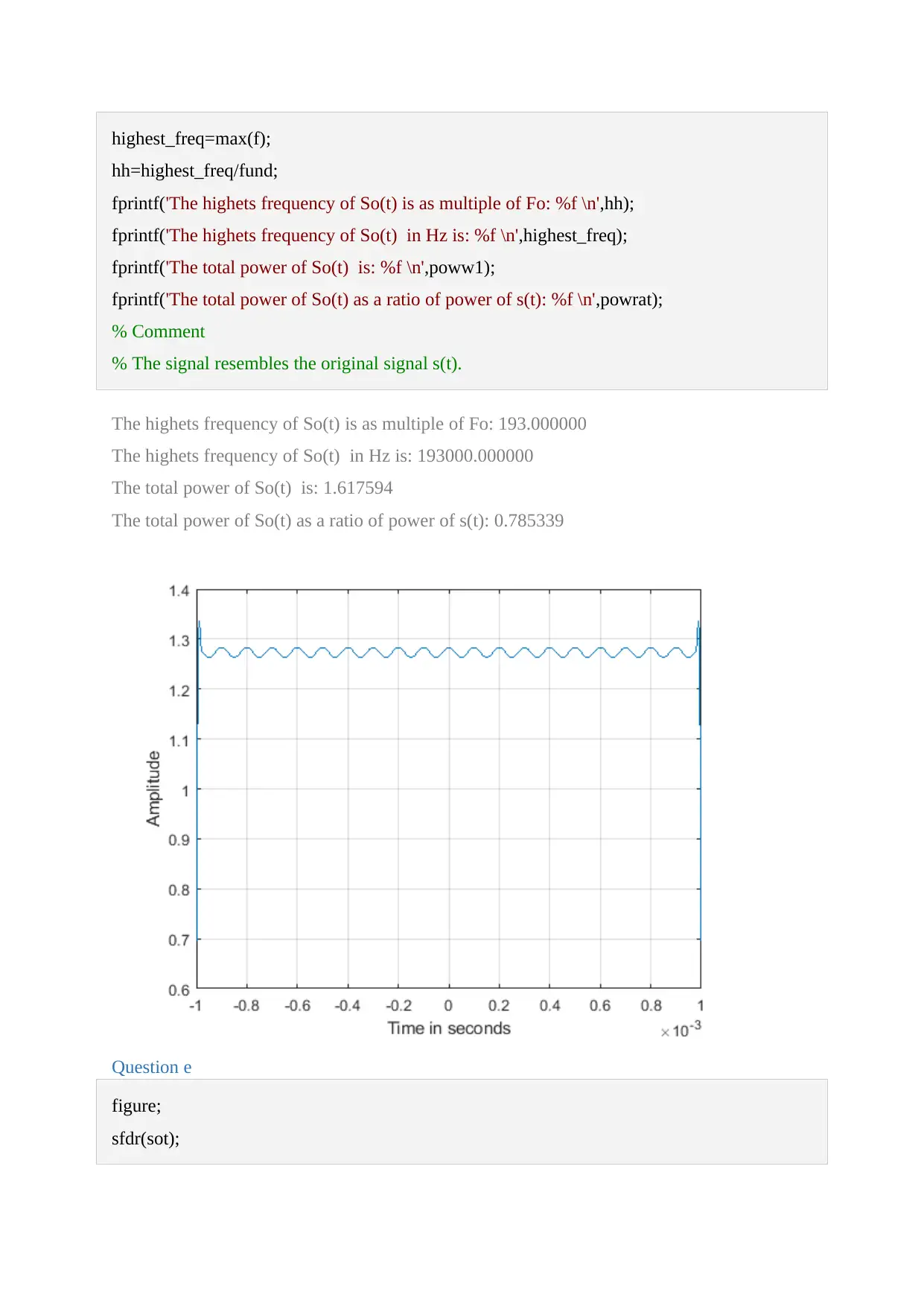
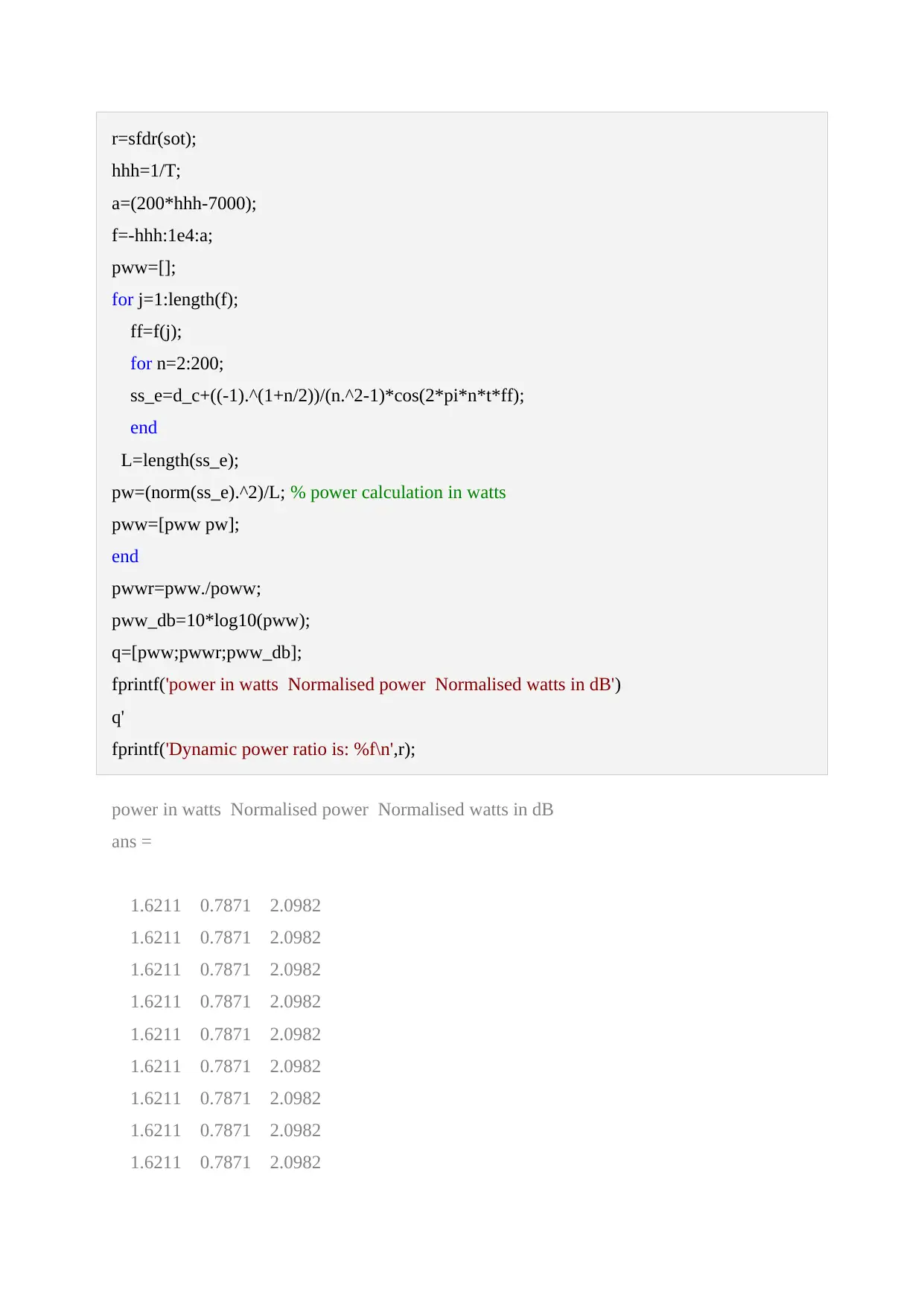
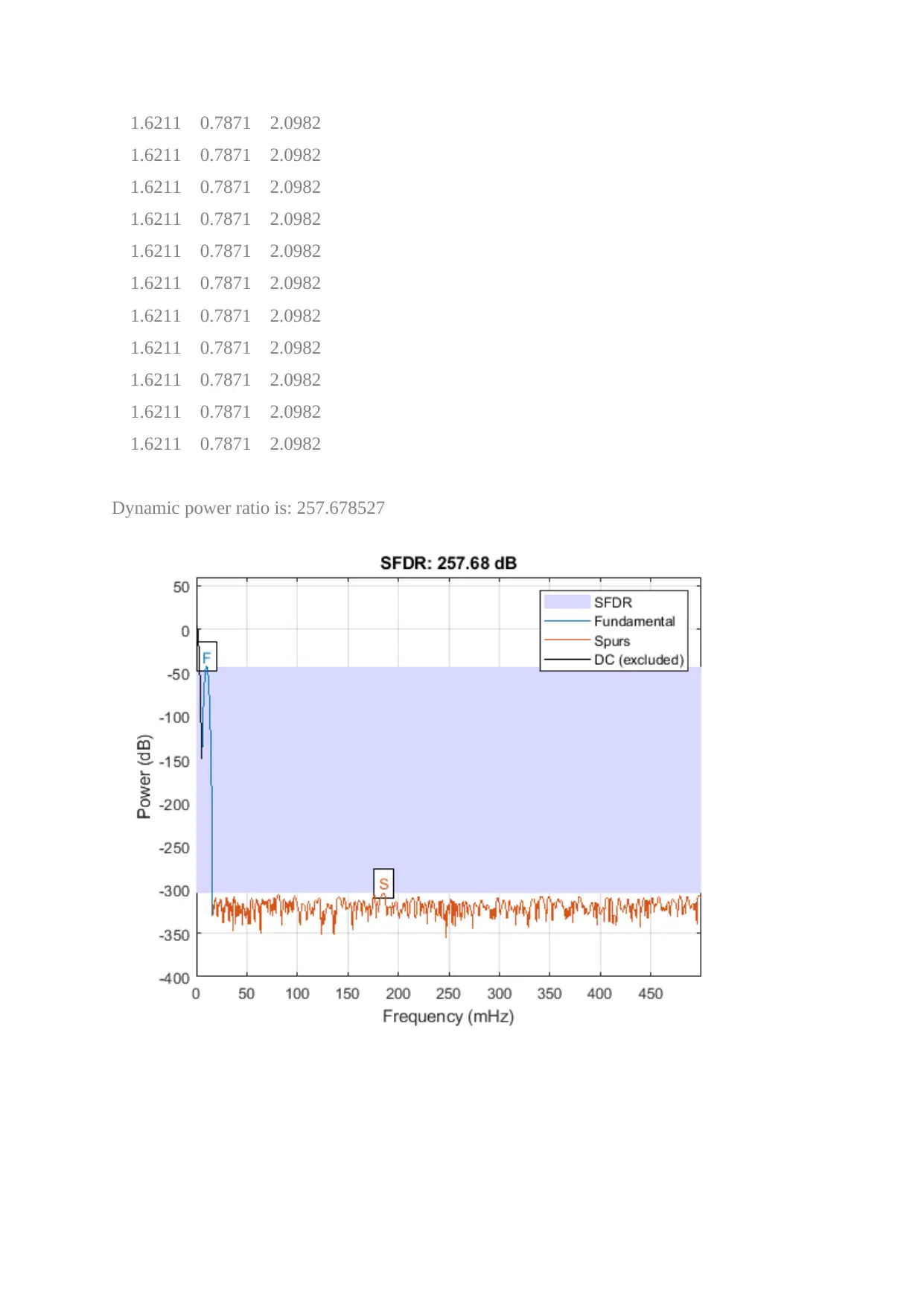
This document presents a comprehensive solution to a Signals and Systems assignment, employing MATLAB for signal analysis and processing. The assignment covers various aspects, including the calculation of DC and AC components, plotting signals, and determining parameters like amplitude, period, and fundamental frequency. The solution delves into the effects of different frequency components, visualizing them through plots and stem diagrams. It also includes the implementation of a low-pass filter and analyzes the filtered signal's characteristics. Furthermore, the assignment calculates power metrics, such as total power and the dynamic power ratio, providing detailed insights into the signal's behavior. The MATLAB code is provided, along with the corresponding plots and numerical results, offering a complete and practical approach to solving the assignment problems. The document includes references to relevant textbooks. This assignment is available on Desklib, a platform providing AI-based study tools.
1 out of 9










![[object Object]](/_next/static/media/star-bottom.7253800d.svg)