Linear Scenario Analysis: Analyzing Age and Height Regression Data

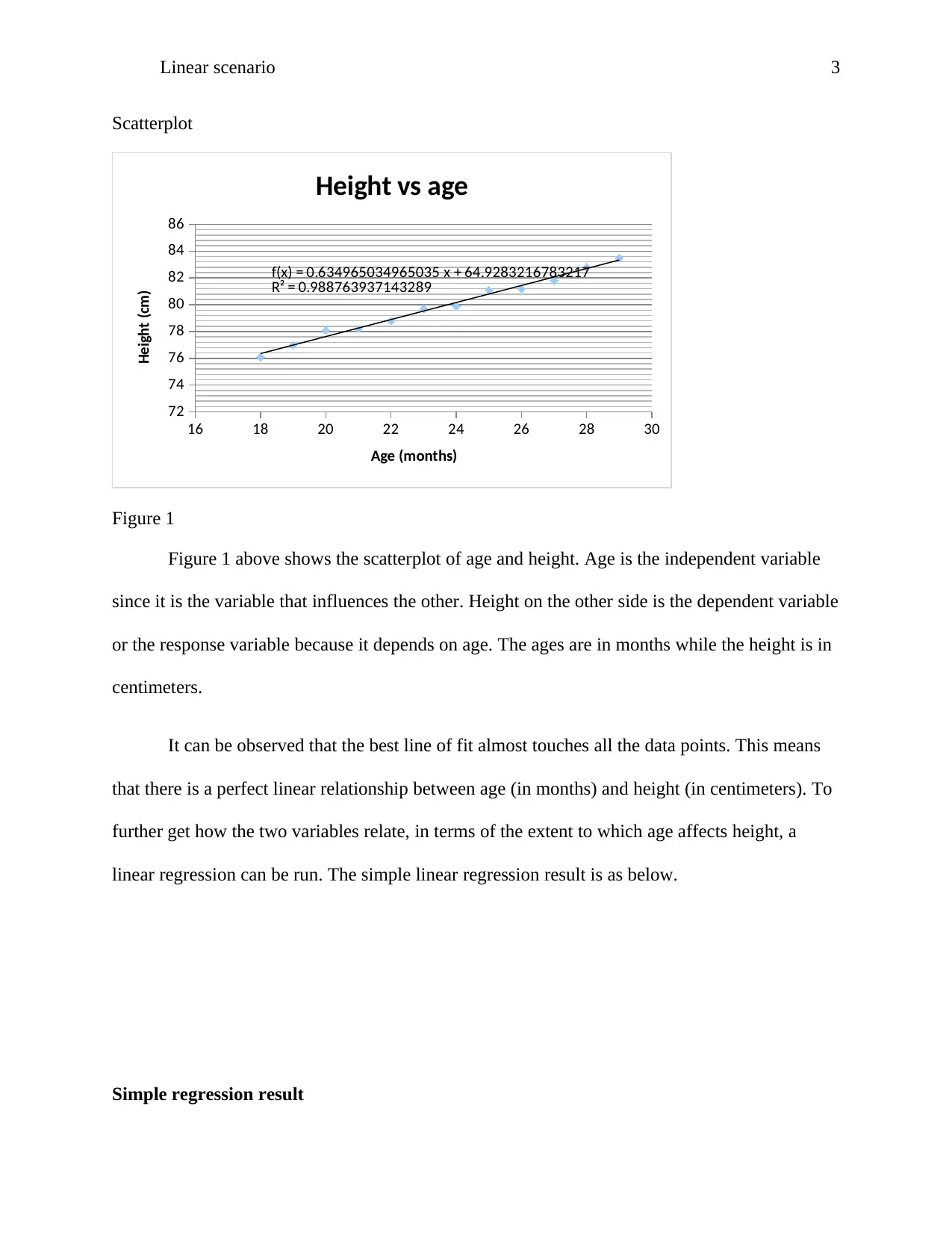
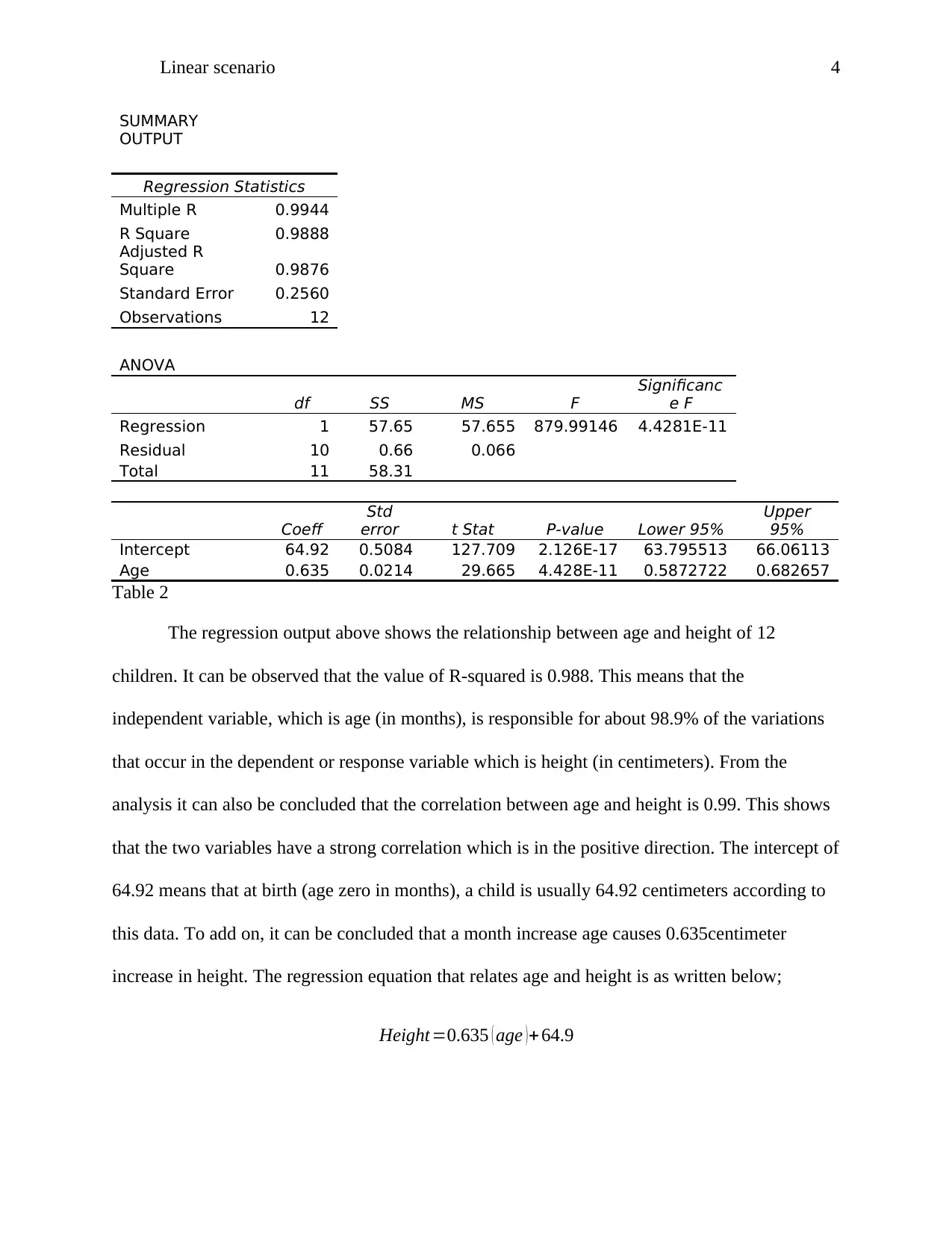
This assignment presents a linear scenario analysis, focusing on the relationship between age and height using a dataset of 12 individuals. The introduction defines linearity and provides a real-world example of age and height correlation. A scatterplot visualizes the data, showing the relationship between age (independent variable) and height (dependent variable). The analysis then proceeds with a simple linear regression, providing key statistical outputs such as R-squared, which indicates the proportion of variance in height explained by age. The R-squared value of 0.988 demonstrates a strong linear relationship. The correlation coefficient of 0.99 further supports a strong positive correlation. The regression equation is derived, and the intercept and coefficient values are interpreted, showing the relationship between age and height. The analysis effectively demonstrates the use of linear regression to model and interpret the relationship between two variables, providing valuable insights into the data and drawing meaningful conclusions.

Linear scenario 1
Linear Scenario
Course code:
Student:
Tutor:

Linear scenario 2
Introduction
Linearity occurs where an increase or decrease in an independent variable causes an increase or a
decrease in the dependent variable. For example, in growth or body development, it is ideally
obvious that an increase in age will always lead to an increase in height. A two year old will be
shorter than a fifteen year old.
This relationship of age and height can be shown graphically using scatterplots. To demonstrate
this, data was collected from among people 12 people of different ages. A scatterplot was drawn
to show the extent of linear relationship between age in years and height in centimeters. The data
is as shown below;
Data table
Age Height
18 76.1
19 77
20 78.1
21 78.2
22 78.8
23 79.7
24 79.9
25 81.1
26 81.2
27 81.8
28 82.8
29 83.5
Table 1 source: https://www3.nd.edu/~busiforc/handouts/Data
Results

Linear scenario 3
Scatterplot
16 18 20 22 24 26 28 30
72
74
76
78
80
82
84
86
f(x) = 0.634965034965035 x + 64.9283216783217
R² = 0.988763937143289
Height vs age
Age (months)
Height (cm)
Figure 1
Figure 1 above shows the scatterplot of age and height. Age is the independent variable
since it is the variable that influences the other. Height on the other side is the dependent variable
or the response variable because it depends on age. The ages are in months while the height is in
centimeters.
It can be observed that the best line of fit almost touches all the data points. This means
that there is a perfect linear relationship between age (in months) and height (in centimeters). To
further get how the two variables relate, in terms of the extent to which age affects height, a
linear regression can be run. The simple linear regression result is as below.
Simple regression result

Linear scenario 4
SUMMARY
OUTPUT
Regression Statistics
Multiple R 0.9944
R Square 0.9888
Adjusted R
Square 0.9876
Standard Error 0.2560
Observations 12
ANOVA
df SS MS F
Significanc
e F
Regression 1 57.65 57.655 879.99146 4.4281E-11
Residual 10 0.66 0.066
Total 11 58.31
Coeff
Std
error t Stat P-value Lower 95%
Upper
95%
Intercept 64.92 0.5084 127.709 2.126E-17 63.795513 66.06113
Age 0.635 0.0214 29.665 4.428E-11 0.5872722 0.682657
Table 2
The regression output above shows the relationship between age and height of 12
children. It can be observed that the value of R-squared is 0.988. This means that the
independent variable, which is age (in months), is responsible for about 98.9% of the variations
that occur in the dependent or response variable which is height (in centimeters). From the
analysis it can also be concluded that the correlation between age and height is 0.99. This shows
that the two variables have a strong correlation which is in the positive direction. The intercept of
64.92 means that at birth (age zero in months), a child is usually 64.92 centimeters according to
this data. To add on, it can be concluded that a month increase age causes 0.635centimeter
increase in height. The regression equation that relates age and height is as written below;
Height=0.635 ( age )+ 64.9