Linear Programming Assignment Solution for Business Development
VerifiedAdded on 2020/04/21
|10
|1116
|68
Homework Assignment
AI Summary
This document presents a comprehensive solution to a linear programming assignment. The solution addresses two main problems. The first problem involves determining the optimal purchase of black and orange beads to minimize cost while meeting certain constraints, solved using the graphical method. The second problem employs the simplex method to maximize an objective function subject to constraints, involving the introduction of slack, surplus, and artificial variables. The solution includes iterative steps, optimal solutions, and sensitivity analysis, determining the range of labor hours and formulating the dual problem. The assignment covers key concepts in business development, optimization, and resource allocation.

Running Head: LINEAR PROGRAMMING ASSIGNNMENT
Linear Programming Assignment
Name of the Student
Name of the University
Author Note
Linear Programming Assignment
Name of the Student
Name of the University
Author Note
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

1LINEAR PROGRAMMING ASSIGNNMENT
Answer 1
(a) The decision variables involved in this problem are black beads and orange beads.
(b) Let x1 be denoted as black beads and x2 be denoted as orange beads. The objective
function can be given as:
Minimize Z=1.50 x1+ x2
Subject ¿ the constraints :
2 x1 + x2 ≥ 12
2 x1 + x2 ≤ 24
x1 ≥ 5
Again, the length of the beads cannot be negative. Hence the non-negativity constraints:
x1 ≥ 0 , x2 ≥ 0
(c) The LPP can be solved by graphical method in the following method:
Let L1: 2 x1 + x2 = 12
Now, the origin, O: (0, 0) satisfies (2 * 0) + (1 * 0) = 0 < 12
Therefore, origin does not satisfy the inequality 2 x1 + x2 ≥ 12
Hence, 2 x1 + x2 ≥ 12 is satisfied by all points on L1 and on the non-origin side of L1
Let L2: 2 x1 + x2 = 24
Now, the origin, O: (0, 0) satisfies (2 * 0) + (1 * 0) = 0 < 24
Therefore, origin satisfies the inequality 2 x1 + x2 ≤ 24
Hence, 2 x1 + x2 ≤ 24 is satisfied by all points on L2 and on the origin side of L2
Let L3: x1 = 5
Now, the origin, O: (0, 0) satisfies (0) < 5
Answer 1
(a) The decision variables involved in this problem are black beads and orange beads.
(b) Let x1 be denoted as black beads and x2 be denoted as orange beads. The objective
function can be given as:
Minimize Z=1.50 x1+ x2
Subject ¿ the constraints :
2 x1 + x2 ≥ 12
2 x1 + x2 ≤ 24
x1 ≥ 5
Again, the length of the beads cannot be negative. Hence the non-negativity constraints:
x1 ≥ 0 , x2 ≥ 0
(c) The LPP can be solved by graphical method in the following method:
Let L1: 2 x1 + x2 = 12
Now, the origin, O: (0, 0) satisfies (2 * 0) + (1 * 0) = 0 < 12
Therefore, origin does not satisfy the inequality 2 x1 + x2 ≥ 12
Hence, 2 x1 + x2 ≥ 12 is satisfied by all points on L1 and on the non-origin side of L1
Let L2: 2 x1 + x2 = 24
Now, the origin, O: (0, 0) satisfies (2 * 0) + (1 * 0) = 0 < 24
Therefore, origin satisfies the inequality 2 x1 + x2 ≤ 24
Hence, 2 x1 + x2 ≤ 24 is satisfied by all points on L2 and on the origin side of L2
Let L3: x1 = 5
Now, the origin, O: (0, 0) satisfies (0) < 5
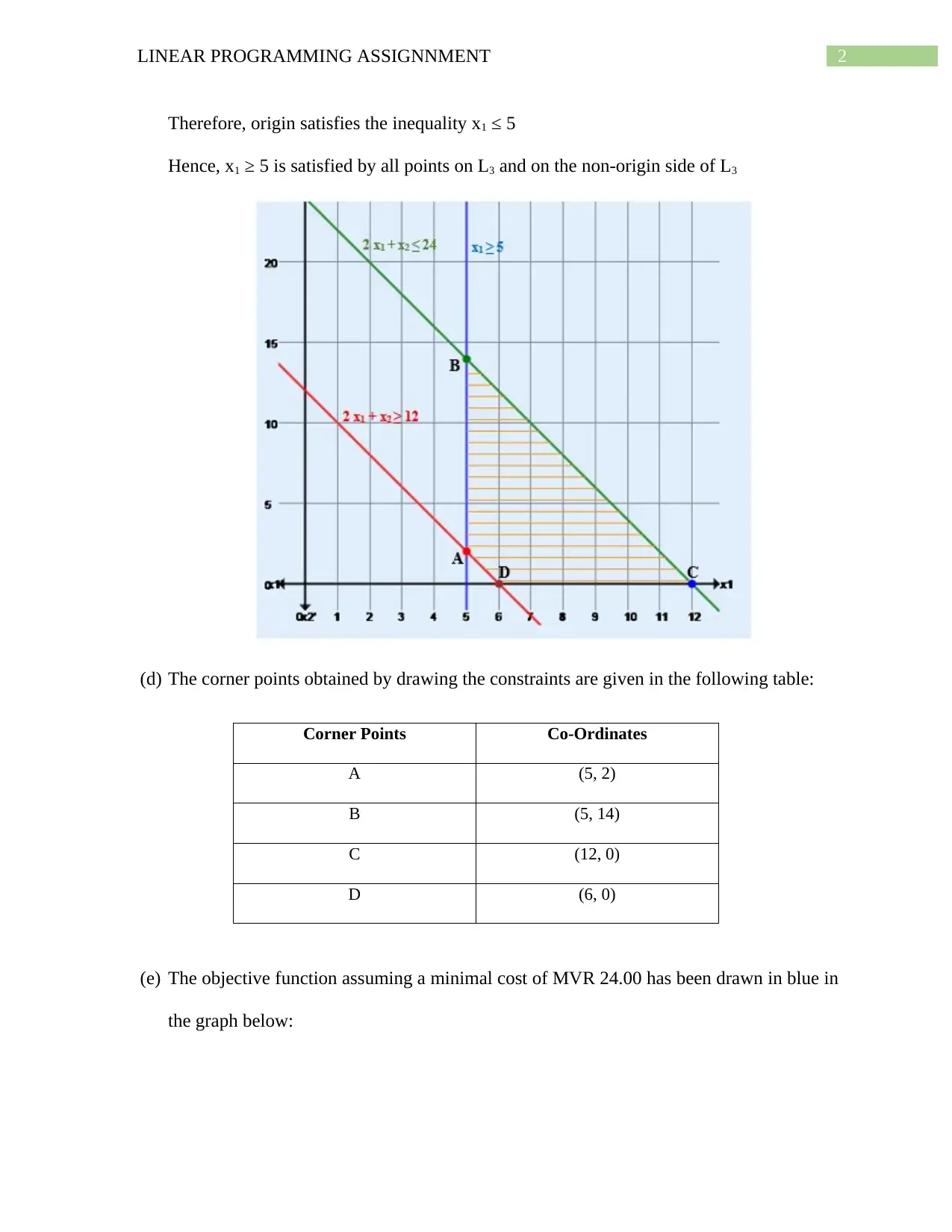
2LINEAR PROGRAMMING ASSIGNNMENT
Therefore, origin satisfies the inequality x1 ≤ 5
Hence, x1 ≥ 5 is satisfied by all points on L3 and on the non-origin side of L3
(d) The corner points obtained by drawing the constraints are given in the following table:
Corner Points Co-Ordinates
A (5, 2)
B (5, 14)
C (12, 0)
D (6, 0)
(e) The objective function assuming a minimal cost of MVR 24.00 has been drawn in blue in
the graph below:
Therefore, origin satisfies the inequality x1 ≤ 5
Hence, x1 ≥ 5 is satisfied by all points on L3 and on the non-origin side of L3
(d) The corner points obtained by drawing the constraints are given in the following table:
Corner Points Co-Ordinates
A (5, 2)
B (5, 14)
C (12, 0)
D (6, 0)
(e) The objective function assuming a minimal cost of MVR 24.00 has been drawn in blue in
the graph below:
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
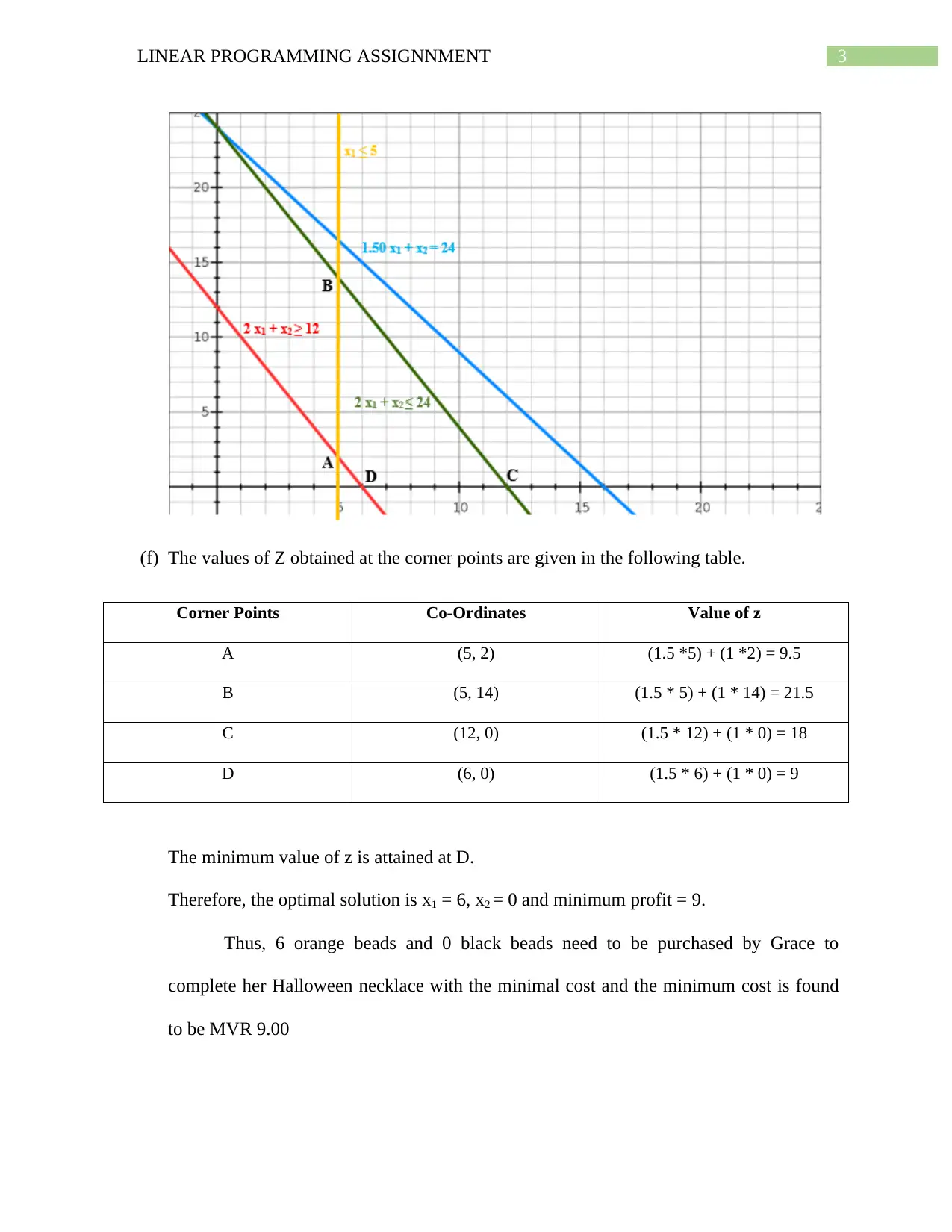
3LINEAR PROGRAMMING ASSIGNNMENT
(f) The values of Z obtained at the corner points are given in the following table.
Corner Points Co-Ordinates Value of z
A (5, 2) (1.5 *5) + (1 *2) = 9.5
B (5, 14) (1.5 * 5) + (1 * 14) = 21.5
C (12, 0) (1.5 * 12) + (1 * 0) = 18
D (6, 0) (1.5 * 6) + (1 * 0) = 9
The minimum value of z is attained at D.
Therefore, the optimal solution is x1 = 6, x2 = 0 and minimum profit = 9.
Thus, 6 orange beads and 0 black beads need to be purchased by Grace to
complete her Halloween necklace with the minimal cost and the minimum cost is found
to be MVR 9.00
(f) The values of Z obtained at the corner points are given in the following table.
Corner Points Co-Ordinates Value of z
A (5, 2) (1.5 *5) + (1 *2) = 9.5
B (5, 14) (1.5 * 5) + (1 * 14) = 21.5
C (12, 0) (1.5 * 12) + (1 * 0) = 18
D (6, 0) (1.5 * 6) + (1 * 0) = 9
The minimum value of z is attained at D.
Therefore, the optimal solution is x1 = 6, x2 = 0 and minimum profit = 9.
Thus, 6 orange beads and 0 black beads need to be purchased by Grace to
complete her Halloween necklace with the minimal cost and the minimum cost is found
to be MVR 9.00
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

4LINEAR PROGRAMMING ASSIGNNMENT
Answer 2
(a)
The problem has been given as:
Max Z=6 x1 +8 x2
Subject ¿ the constraints: 30 x1+20 x2 ≤ 300
5 x1+10 x2 ≤ 110
¿ x1 , x2 ≥ 0
The problem now has to be converted into a standard form by inserting the slack variables,
surplus variables and artificial variables wherever necessary.
In this problem, the objective is to maximize and the constraints are all of the type ≤. Thus, slack
variables S1 and S2will have to be introduced in constraints 1 and 2 respectively.
After introduction of the slack variables, the problem becomes as follows:
Max Z=6 x1 +8 x2+0 S1+ 0 S2
Subject ¿ the constraints: 30 x1+20 x2 +S1=300
5 x1+10 x2+S2=110
¿ x1 , x2 , S1 , S2 ≥0
Answer 2
(a)
The problem has been given as:
Max Z=6 x1 +8 x2
Subject ¿ the constraints: 30 x1+20 x2 ≤ 300
5 x1+10 x2 ≤ 110
¿ x1 , x2 ≥ 0
The problem now has to be converted into a standard form by inserting the slack variables,
surplus variables and artificial variables wherever necessary.
In this problem, the objective is to maximize and the constraints are all of the type ≤. Thus, slack
variables S1 and S2will have to be introduced in constraints 1 and 2 respectively.
After introduction of the slack variables, the problem becomes as follows:
Max Z=6 x1 +8 x2+0 S1+ 0 S2
Subject ¿ the constraints: 30 x1+20 x2 +S1=300
5 x1+10 x2+S2=110
¿ x1 , x2 , S1 , S2 ≥0

5LINEAR PROGRAMMING ASSIGNNMENT
Iteration 1 C j 6 8 0 0
B CB X B x1 x2 S1 S2 Minimum Ratio
XB
x2
S1 0 300 30 20 1 0 300
20 =15
S2 0 110 5 (10) 0 1 110
10 =11→
Z = 0 Z j 0 0 0 0
C j−Z j 6 8 ↑ 0 0
The maximum positive value of C j−Z j is 8 and 8 belongs to the column of x2 . Thus, the
entering variable will be x2
The minimum ratio is thus observed to be 11 and it belongs to the row of S2. Thus, the exiting
variable will be S2 .
Thus the key element will be the intersection of x2 and S2, which is 10.
Thus, the row of the new arrangement will be as follows:
New row 2 = Old row 2 / 10
New row 1 = Old row 1 – 20 * New row 2
The updated table is given as follows:
Iteration 2 C j 6 8 0 0
B CB X B x1 x2 S1 S2 Minimum Ratio
XB
x1
Iteration 1 C j 6 8 0 0
B CB X B x1 x2 S1 S2 Minimum Ratio
XB
x2
S1 0 300 30 20 1 0 300
20 =15
S2 0 110 5 (10) 0 1 110
10 =11→
Z = 0 Z j 0 0 0 0
C j−Z j 6 8 ↑ 0 0
The maximum positive value of C j−Z j is 8 and 8 belongs to the column of x2 . Thus, the
entering variable will be x2
The minimum ratio is thus observed to be 11 and it belongs to the row of S2. Thus, the exiting
variable will be S2 .
Thus the key element will be the intersection of x2 and S2, which is 10.
Thus, the row of the new arrangement will be as follows:
New row 2 = Old row 2 / 10
New row 1 = Old row 1 – 20 * New row 2
The updated table is given as follows:
Iteration 2 C j 6 8 0 0
B CB X B x1 x2 S1 S2 Minimum Ratio
XB
x1
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

6LINEAR PROGRAMMING ASSIGNNMENT
S1 0 80 (20) 0 1 -2 80
20 =4 →
x2 8 11 ½ 1 0 1
10
11
1
2
=22
Z = 0 Z j 4 8 0 4
5
C j−Z j 2 ↑ 0 0 −4
5
The maximum positive value of C j−Z j is 2 and 2 belongs to the column of x1 . Thus, the
entering variable will be x1
The minimum ratio is thus observed to be 4 and it belongs to the row of S1. Thus, the exiting
variable will be S1 .
Thus the key element will be the intersection of x1 and S1, which is 10.
Thus, the row of the new arrangement will be as follows:
New row 1 = Old row 1 / 20
New row 2 = Old row 2 – 1
2* New row 2
The updated table is given as follows:
Iteration 3 C j 6 8 0 0
B CB X B x1 x2 S1 S2 Minimum Ratio
x1 6 4 1 0 1
20
−1
10
x2 8 9 0 1 −1
40
3
20
S1 0 80 (20) 0 1 -2 80
20 =4 →
x2 8 11 ½ 1 0 1
10
11
1
2
=22
Z = 0 Z j 4 8 0 4
5
C j−Z j 2 ↑ 0 0 −4
5
The maximum positive value of C j−Z j is 2 and 2 belongs to the column of x1 . Thus, the
entering variable will be x1
The minimum ratio is thus observed to be 4 and it belongs to the row of S1. Thus, the exiting
variable will be S1 .
Thus the key element will be the intersection of x1 and S1, which is 10.
Thus, the row of the new arrangement will be as follows:
New row 1 = Old row 1 / 20
New row 2 = Old row 2 – 1
2* New row 2
The updated table is given as follows:
Iteration 3 C j 6 8 0 0
B CB X B x1 x2 S1 S2 Minimum Ratio
x1 6 4 1 0 1
20
−1
10
x2 8 9 0 1 −1
40
3
20
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
7LINEAR PROGRAMMING ASSIGNNMENT
Z = 96 Z j 6 8 1
10
3
5
C j−Z j 0 0 −1
10
−3
5
In the table of the third iteration, all C j−Z j ≤ 0.
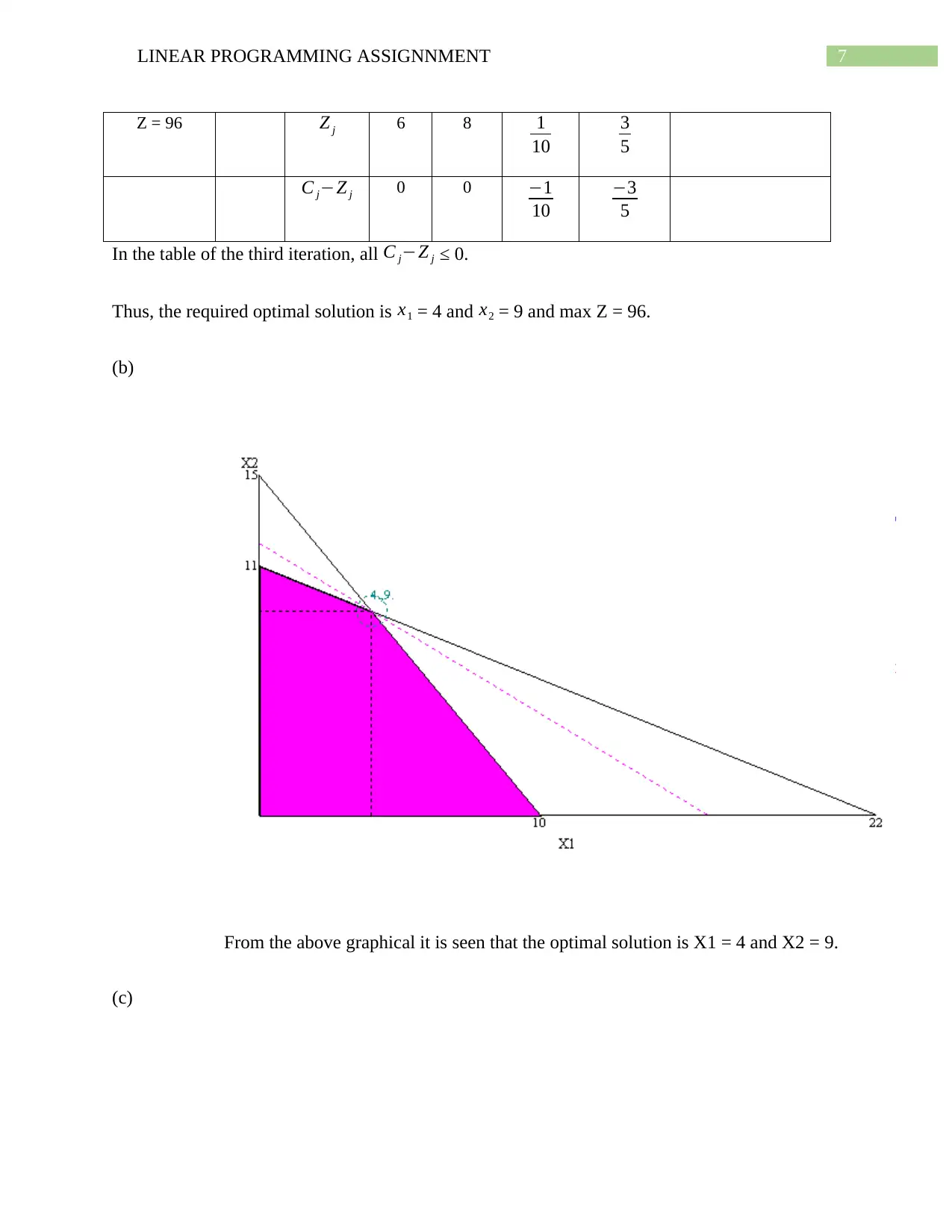
Thus, the required optimal solution is x1 = 4 and x2 = 9 and max Z = 96.
(b)
From the above graphical it is seen that the optimal solution is X1 = 4 and X2 = 9.
(c)
Z = 96 Z j 6 8 1
10
3
5
C j−Z j 0 0 −1
10
−3
5
In the table of the third iteration, all C j−Z j ≤ 0.
Thus, the required optimal solution is x1 = 4 and x2 = 9 and max Z = 96.
(b)
From the above graphical it is seen that the optimal solution is X1 = 4 and X2 = 9.
(c)
8LINEAR PROGRAMMING ASSIGNNMENT
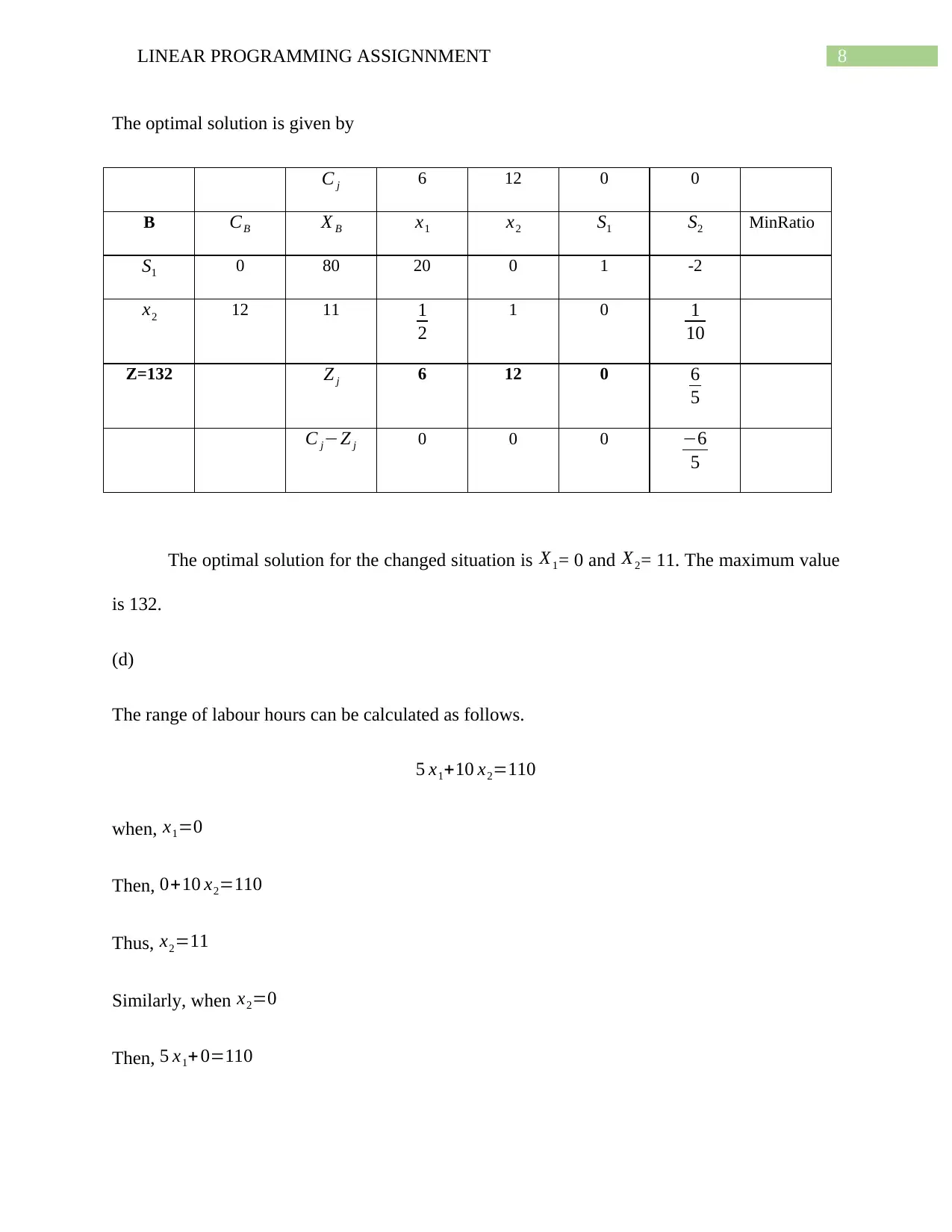
The optimal solution is given by
C j 6 12 0 0
B CB X B x1 x2 S1 S2 MinRatio
S1 0 80 20 0 1 -2
x2 12 11 1
2
1 0 1
10
Z=132 Z j 6 12 0 6
5
C j−Z j 0 0 0 −6
5
The optimal solution for the changed situation is X1= 0 and X2= 11. The maximum value
is 132.
(d)
The range of labour hours can be calculated as follows.
5 x1+10 x2=110
when, x1=0
Then, 0+10 x2=110
Thus, x2=11
Similarly, when x2=0
Then, 5 x1+0=110
The optimal solution is given by
C j 6 12 0 0
B CB X B x1 x2 S1 S2 MinRatio
S1 0 80 20 0 1 -2
x2 12 11 1
2
1 0 1
10
Z=132 Z j 6 12 0 6
5
C j−Z j 0 0 0 −6
5
The optimal solution for the changed situation is X1= 0 and X2= 11. The maximum value
is 132.
(d)
The range of labour hours can be calculated as follows.
5 x1+10 x2=110
when, x1=0
Then, 0+10 x2=110
Thus, x2=11
Similarly, when x2=0
Then, 5 x1+0=110
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
9LINEAR PROGRAMMING ASSIGNNMENT
Thus, x1=22
Thus, the range of Labour hours is 11 to 22 hours.
(e)
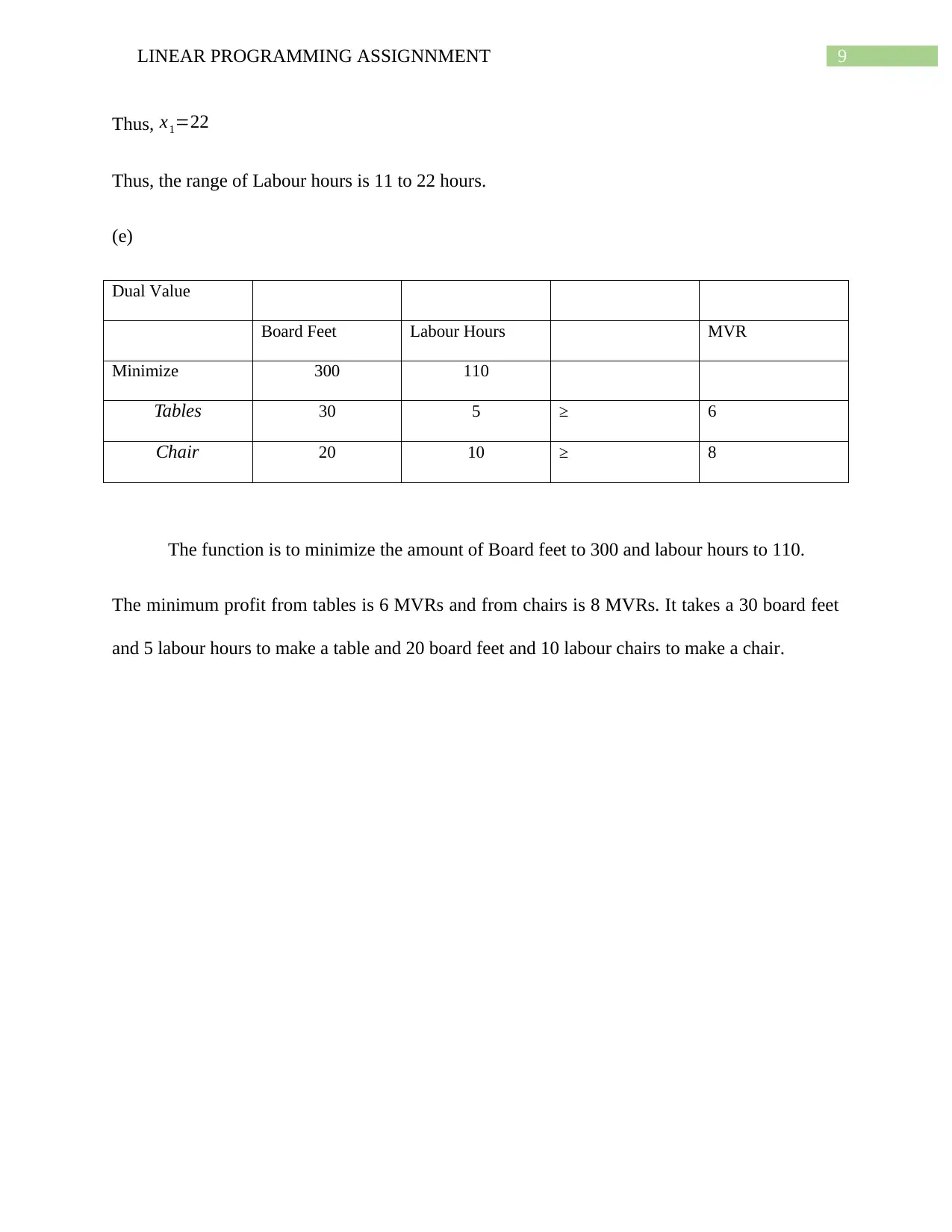
Dual Value
Board Feet Labour Hours MVR
Minimize 300 110
Tables 30 5 ≥ 6
Chair 20 10 ≥ 8
The function is to minimize the amount of Board feet to 300 and labour hours to 110.
The minimum profit from tables is 6 MVRs and from chairs is 8 MVRs. It takes a 30 board feet
and 5 labour hours to make a table and 20 board feet and 10 labour chairs to make a chair.
Thus, x1=22
Thus, the range of Labour hours is 11 to 22 hours.
(e)
Dual Value
Board Feet Labour Hours MVR
Minimize 300 110
Tables 30 5 ≥ 6
Chair 20 10 ≥ 8
The function is to minimize the amount of Board feet to 300 and labour hours to 110.
The minimum profit from tables is 6 MVRs and from chairs is 8 MVRs. It takes a 30 board feet
and 5 labour hours to make a table and 20 board feet and 10 labour chairs to make a chair.
1 out of 10
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.




