Analyzing Income Data by Gender and Education

This assignment analyzes income data for various categories: Men with degrees, Women with degrees, Men without degrees, and Women without degrees. The task involves calculating the median, mode, and range for each category. Additionally, the analysis aims to highlight income trends and potential disparities between genders and education levels.

Assignment
1 | P a g e
Mathematics

Assignment
Contents
SECTION – 1..................................................................................................................................3
Task 1: Skill Audit.......................................................................................................................3
Task 2: Solution of question-1.....................................................................................................4
Task 2: Solution of question-2.....................................................................................................4
Task 3: Online Activity...............................................................................................................4
SECTION – 2..................................................................................................................................5
Task 1: Skill Audit.......................................................................................................................5
Task 2: Solution of question-1.....................................................................................................6
Task 2: Solution of question-1.....................................................................................................6
Task 3: Online Activity...............................................................................................................6
SECTION – 3..................................................................................................................................7
Task 1: Skill Audit.......................................................................................................................7
Task 2: Solution of question-1.....................................................................................................7
Task 2: Solution of question-2.....................................................................................................8
Task 3: Online Activity...............................................................................................................8
SECTION – 4..................................................................................................................................8
Solution of question-1..................................................................................................................8
Solution of question-2..................................................................................................................9
Solution of question-3..................................................................................................................9
Solution of question-5................................................................................................................10
Solution of question-6................................................................................................................10
Solution of question-7................................................................................................................11
Solution of question-8................................................................................................................11
Solution of question-9................................................................................................................12
Solution of question-10..............................................................................................................12
Bibliography..................................................................................................................................14
2 | P a g e

Assignment
SECTION – 1
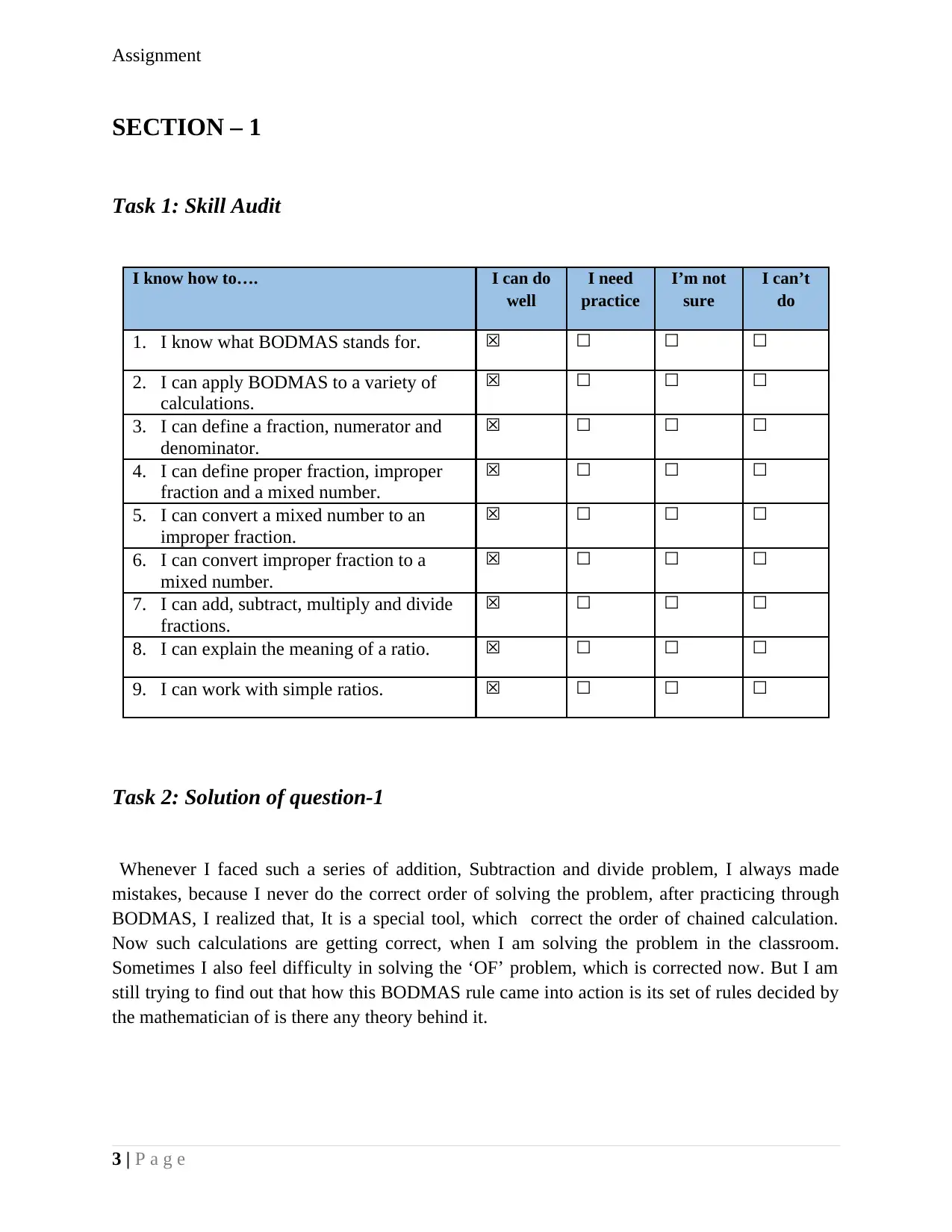
Task 1: Skill Audit
I know how to…. I can do
well
I need
practice
I’m not
sure
I can’t
do
1. I know what BODMAS stands for. ☒ ☐ ☐ ☐
2. I can apply BODMAS to a variety of
calculations.
☒ ☐ ☐ ☐
3. I can define a fraction, numerator and
denominator.
☒ ☐ ☐ ☐
4. I can define proper fraction, improper
fraction and a mixed number.
☒ ☐ ☐ ☐
5. I can convert a mixed number to an
improper fraction.
☒ ☐ ☐ ☐
6. I can convert improper fraction to a
mixed number.
☒ ☐ ☐ ☐
7. I can add, subtract, multiply and divide
fractions.
☒ ☐ ☐ ☐
8. I can explain the meaning of a ratio. ☒ ☐ ☐ ☐
9. I can work with simple ratios. ☒ ☐ ☐ ☐
Task 2: Solution of question-1
Whenever I faced such a series of addition, Subtraction and divide problem, I always made
mistakes, because I never do the correct order of solving the problem, after practicing through
BODMAS, I realized that, It is a special tool, which correct the order of chained calculation.
Now such calculations are getting correct, when I am solving the problem in the classroom.
Sometimes I also feel difficulty in solving the ‘OF’ problem, which is corrected now. But I am
still trying to find out that how this BODMAS rule came into action is its set of rules decided by
the mathematician of is there any theory behind it.
3 | P a g e

Assignment
Task 2: Solution of question-2
My family consists of 5 people including two brothers and a sister, I am in the middle. My
parents had given some of strawberry and told me that Please distribute it into all three with ¼, ¼
and ½ to my elder sister and brother. They ask me to tell the total number of strawberry that I
have distributed.
I realize, If we take 2(1/4) +1/2 = 20, then we can distribute it correctly If I will go through
BODMAS rule, and each kid will get 5, 5, 10 strawberry. But If I distribute it without BODMAS
rule, I find that it the answer comes as ¾ which is meaningless. Then I realized that How
BODMAS is able to rationalize the real world problem.
Task 3: Online Activity
4 | P a g e

Assignment
SECTION – 2
Task 1: Skill Audit
I know how to…. I can
do well
I need
practic
e
I’m not
sure
I can’t
do
10. I can describe the
relationship between fractions,
decimals and percentages.
☒ ☐ ☐ ☐
11. I can identify the decimal
equivalent of a percent.
☒ ☐ ☐ ☐
12. I can identify the fractional
equivalent of a percent.
☒ ☐ ☐ ☐
13. I can determine which
concepts and procedures are
needed to complete each
practice exercise.
☒ ☐ ☐ ☐
14. I can compute answers by
applying appropriate formulas
and procedures.
☒ ☐ ☐ ☐
15. I can construct a simple
index.
☒ ☐ ☐ ☐
16. I can interpret indexes to
identify trends in a data set.
☒ ☐ ☐ ☐
Task 2: Solution of question-1
The use of decimal, percentage and index number is found to be very useful, from childhood
these jargon was making me speechless when My Dad always talks with someone in decimal
like 7.2 , 8.9% etc. In investment point of view, it was always being discussed in profit and loss
with a percentage. It was awesome to know that these entities are always converted to each other.
The addition of number with same index was awesome; it is really making calculation shorter as
compared to previous one. Now most of the transaction happening around us is looking
meaningfully, especially, discount etc., which, shopkeeper giving during buying a product.
5 | P a g e

Assignment
Task 2: Solution of question-1
I always hear from my doctors that, my fever is 98.6 which are supposed to be normal. Amazon
is giving a 8% discount with my father’s credit card. Write the 25 much easier that writing
2*2*2*2*2= 32. So these are the some of the simple problem. Which I realize that is useful by
knowing the above concept.
Task 3: Online Activity
SECTION – 3
Task 1: Skill Audit
I know how to…. I can
do well
I need
practic
e
I’m not
sure
I can’t
do
17. I know how to calculate a
mean.
☒ ☐ ☐ ☐
18. I know how to calculate a
median.
☒ ☐ ☐ ☐
19. I know how to calculate a
mode.
☒ ☐ ☐ ☐
20. I know how to calculate ☒ ☐ ☐ ☐
6 | P a g e

Assignment
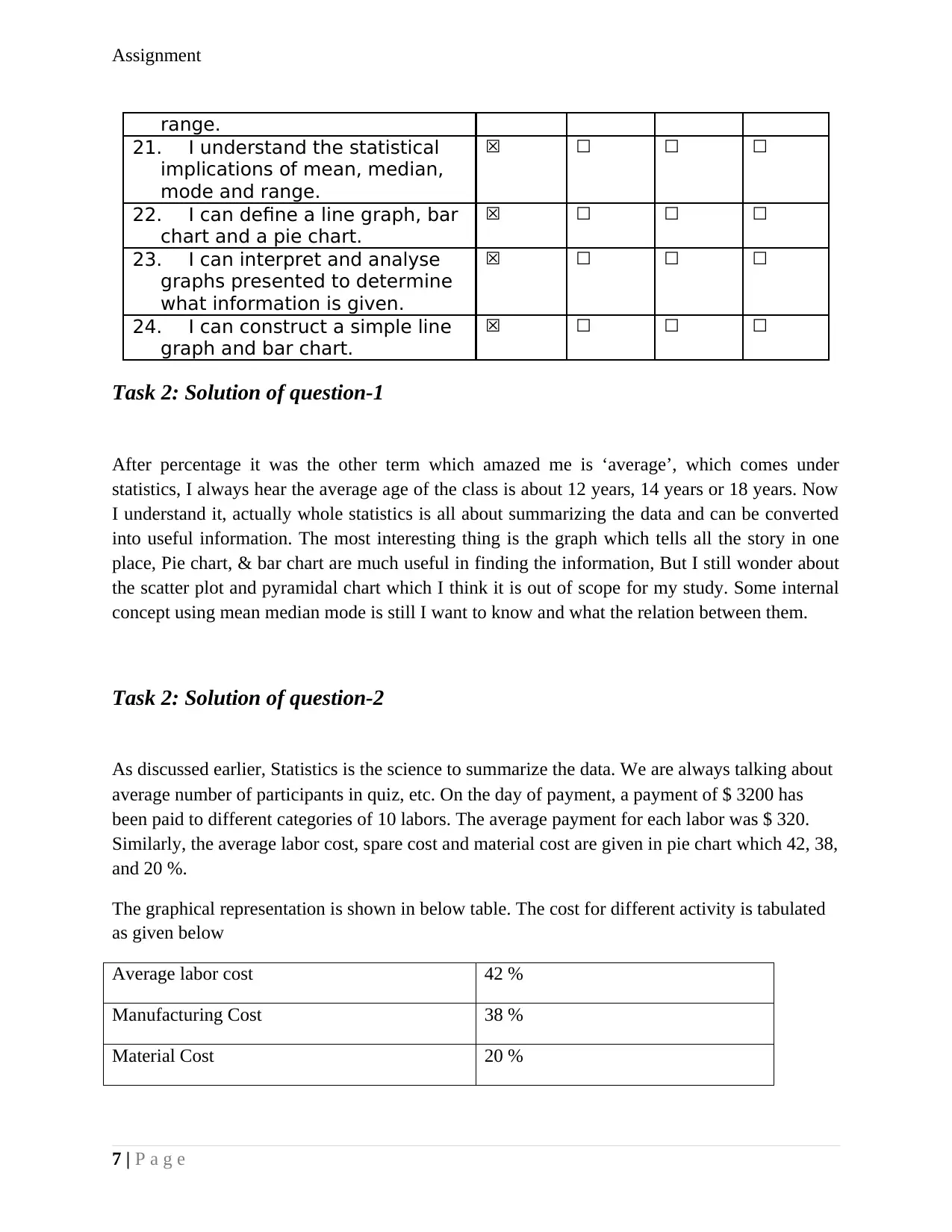
range.
21. I understand the statistical
implications of mean, median,
mode and range.
☒ ☐ ☐ ☐
22. I can define a line graph, bar
chart and a pie chart.
☒ ☐ ☐ ☐
23. I can interpret and analyse
graphs presented to determine
what information is given.
☒ ☐ ☐ ☐
24. I can construct a simple line
graph and bar chart.
☒ ☐ ☐ ☐
Task 2: Solution of question-1
After percentage it was the other term which amazed me is ‘average’, which comes under
statistics, I always hear the average age of the class is about 12 years, 14 years or 18 years. Now
I understand it, actually whole statistics is all about summarizing the data and can be converted
into useful information. The most interesting thing is the graph which tells all the story in one
place, Pie chart, & bar chart are much useful in finding the information, But I still wonder about
the scatter plot and pyramidal chart which I think it is out of scope for my study. Some internal
concept using mean median mode is still I want to know and what the relation between them.
Task 2: Solution of question-2
As discussed earlier, Statistics is the science to summarize the data. We are always talking about
average number of participants in quiz, etc. On the day of payment, a payment of $ 3200 has
been paid to different categories of 10 labors. The average payment for each labor was $ 320.
Similarly, the average labor cost, spare cost and material cost are given in pie chart which 42, 38,
and 20 %.
The graphical representation is shown in below table. The cost for different activity is tabulated
as given below
Average labor cost 42 %
Manufacturing Cost 38 %
Material Cost 20 %
7 | P a g e

Assignment
The above table can be represented graphically in the form of Pie chart.(as given below)
42%
38%
20%
Cost for various activity
Average labor cost Manufacturing Cost Material Cost
Task 3: Online Activity
SECTIO
N – 4
Solution of question-1
As given in question,
In 2011, the awarded no of degrees = 350800
In 2000, the awarded no of degrees = 243243
The difference in on decade = 350800 – 243246 = 107554
The percentage increase in awards = 107554 x 100/ 243246 = 44.22 % Ans
8 | P a g e

Assignment
Solution of question-2
Number of female in 1980 = 25319
% increase = 33.76%
Increase in numbers = 25319 * 33.76/100 = 8547.7 ≈ 8548
Female first degree graduate 1990 = 25319+8548 = 33867 Ans
Solution of question-3
Suppose x is the no of students in 1999
Students in 2000 = x+ 4.7x/100 …(i)
Students admitted in 2000 = 986267 ….(ii)
Since both the equation are equal
X+ 4.7x/100 = 986267
104.7 x
100 =986267
x= 986267∗100
104.7 =¿941993.3
Number of students admitted in 1999 = 941993 Ans
Solution of question-4
As given in question,
The percentage given for each of the specialty is as follows,
Computer science – 27.5 %
Medicine -- 7%
Engineering -- 5%
9 | P a g e

Assignment
Biological -- 14%
Law -- 10.9%
B&A -- 35.6
First we have to calculate the % for Law – 100 – (27.5 + 7 + 5+ 14 + 35.6) = 10.9
a) The second highest no of students
= 27.5 % for computer science = 27.5
100 x 734037=201860 Ans
b) The lowest no of students is Engineering = 5% = 5
100 x 734037=36701 Ans
c) The % for Law is = 10.9 % = 10.9
100 x 734037=80010 Ans
d) The number of students in B&A = 35.6
100 x 734037=261317 Ans
e) The no of biological students = 14
100 x 734037=102765
The increase no of students in computer science = 201860 – 102765 = 99095 Ans
Solution of question-5
a) As per bar chart the number of students living in England and working part time = 19%
b) percentage of students living in Royal Greenwich, and are in employment full-time =
53% Ans
c) Full time employment in England = 54%
Self-employed in London = 14 %
% increase in full time in England = 54 – 14 = 40% Ans
Solution of question-6
10 | P a g e

Assignment
In 2011, Part time post graduate students = 127750 out of total 1145435 students
Therefore, % for Part time post graduate = 127750
1145435 x 100=11 % Ans
Solution of question-7
No of Post graduate part time = 107950
No of undergraduate full time = 513295
Ratio of Both = 107950 / 513295 = 1:4.75 1: 5 Ans
Solution of question-8
The specified data for 2005/06 to 2010/11 is
Year Postgraduate
part-time
Postgraduate
full-time
Undergraduat
e part-time
Undergraduat
e full-time Total
2010/1
1 127,750 207,595 301,025 509,065 1,145,435
2009/1
0 132,790 200,880 334,820 516,770 1,185,260
2008/0
9 129,055 177,595 344,775 493,425 1,144,850
2007/0
8 116,570 161,015 332,320 458,575 1,068,475
2006/0
7 116,220 162,575 341,035 437,775 1,057,610
2005/0
6 114,940 155,665 337,240 450,485 1,058,330
a) The mean for Part time undergraduate Students =
(301,025+334,820+344,775+332,320+341,035+ 337,240) / 2= 331869
b) The median for Part time undergraduate students
Sorting the above data 301,025, 332320, 332320, 337240, 341035, 344775
Median will be calculated as (n+1)2th term = (6+1)/2 = 3.5
We have to take average of two term i.e. 3rd and 4th = (332320+337240)/2 = 334780
11 | P a g e

Assignment
Therefore median = 334780.
c) The mode of the given sample = The most no of data appears in the sample, in this
condition it is 332320 Ans
Solution of question-9
Earning of graduate female of 34 years old = £16.50
Earning of non-graduate female of 34 years old = £9.8
Difference in earning = 16.5 - 9.8 = 6.7
% of more earning = 6.7
9.8 x 100=68.37 % Ans
Solution of question-10
a) Mean for Men with degree = ∑
Age=65
Age=22
fx
n
840.90
43 = 19.56
Mean for Women with degree = 671.10
43 =15.61
Mean for men without degree = 511
43 =11.88
Mean for women without degree = 393.2
43 =9.14 Ans
b) Median
12 | P a g e

Assignment
for Men with degree
First we have to short the data which is as follows - 9.10 10.20 11.40 12.50 13.50
14.50 15.50 16.70 17.70 18.40 18.90 19.20 19.20 19.20 19.50 19.70 19.70
20.20 20.40 20.50 20.60 20.80 21.00 21.20 21.30 21.40 21.60 21.90 22.00
22.10 22.10 22.20 22.20 22.20 22.30 22.30 22.30 22.30 22.50 22.50 22.60
22.70 22.80
There are 43 data then we have to find = (n+1)/2th data set which is = (43+1)/2 = 22nd data
which is 20.8.
Similarly soring the other three criteria we will find the 22nd term as median
Median for women with degree: 8.80 9.80 10.80 11.60 12.50 13.20 14.00 14.80
15.40 15.40 15.50 15.60 15.60 15.60 15.70 16.00 16.20 16.30 16.40 16.50
16.50 16.50 16.50 16.60 16.60 16.60 16.60 16.70 16.70 16.70 16.80 16.80
16.80 16.80 16.80 16.80 16.90 16.90 16.90 16.90 17.00 17.00 17.00
The median will be = 16.50
Similarly for Men without degree median = 12.5
And Women without degree = 9.20
c) Mode
For Men with degree,
The maximum number of repetitive data is 22.3 which comes as four times, therefore mode =
22.3
For Women with degree,
The maximum number of repetitive data is 16.5 which comes as four times, therefore mode =
16.8
For Men without degree,
The maximum number of repetitive data is 13.2 which comes as five times, therefore mode =
13.2
For Women without degree,
The maximum number of repetitive data is 8.7 which comes as three times, therefore mode = 8.7
d) Range
13 | P a g e

Assignment
Category Maximum No Minimum No Range = max - min
Men with degree 22.8 9.1 13.7
Women with degree 17 8.8 8.2
Men without degree 13.5 8.1 5.4
Women without degree 10.1 7.4 2.7
Bibliography
14 | P a g e

Assignment
Blitzer, R, 2018, College Algebra. 7th ed, Newyork: Pearson Education,.
Kaufmann, J, E, 2014. Intermediate algebra. 1st ed, New York: Cengage Learning.
Math, B, H, S, 2013, Jim Elande, New York: Xlibris.
Wentworth, G, 2009, Junior High School Mathematics. New York: BiblioBazaar.
15 | P a g e