Assignment About Mathematics

Mathematics Assignment:
Student Name:
Instructor Name:
Course Number:
8th January 2020

Q1)
csc θ= −12
7
1
sin θ =−12
7
sin θ=−7
12
7 12
θ
√ 95
√122−72= √95
Since θ lies in the fourth quadrant, its cosine and tangent will be positive and negative respectively.
cos θ= √95
12 = 9.747
12
tanθ= −7
√ 95 = −7
9.747
tanθ= −7
9.747
sec θ= 1
cosθ = 1
9.747
12
= 12
9.747
sec θ= 12
9.747

cot θ= 1
tanθ = 1
−7
9.747
=−9.747
7
cot θ=−9.747
7
Q2a)
C ( x )=0.3456 x
C ( 35 )=0.3456 ( 35 )=12.096
C ( 35 )=12.096
b)
Domain of C ( x ) is from x=0 to x <75
Q3a)
The function g touches the x axis twice at points (-1, 0) and (5, 0). We may therefore say that it
is a quadratic equation in x with roots x=−1∧x=5.Therefore we have
( x +1 ) ( x−5 )=0
¿ x2−4 x−5=0
Assuming that g takes the form g( x )=a x2 +bx+ c we get
g ( x )=x2−4 x−5
The function f is a curve with stationary point at (3 , 0).
Assuming that f takes the form f ( x)=a x2 +bx +c.
At the stationary point f ' ( x )=2 ax +b=0
f ' ( 3 ) =2 a(3)+b=0
6 a+b=0 ………………………………………..i
At (3, 0)
f ( 3 )=a (3)2 +3 b+ c
0=9 a+3 b+c ……………………………ii

f Also passes through (4 ,−1)
f ( 4 ) =a(4)2 +4 b+c
−1=16 a+4 b+c ……………………………iii
iii minus ii gives 7 a+ b=−1
7 a+ b=−1 … …… … …… . iv
Solving i and iv simultaneously by taking iv minus i we have
a=−1
7 a+ b=−1
7(−1)+b=−1
b=−1+7=6
−1=16 (−1)+ 4 (6)+ c
−1+16−24=c
−9=c
f ( x ) =a x2 +bx +c=−x2 +6 x−9
f ( x )=−x2 +6 x−9
f ( x )=−x2 +6 x−9
g ( x )=x2−4 x−5
g ( x )=x2−4 x−5
g ( 1 )=12−4 ( 1 )−5=−8
g ( 1 )=−8
f ( x )=−x2 +6 x−9
f ( 1 ) =−12+ 6 ( 1 )−9=−4
f ( 1 ) =−4
( f ° g ) ( 1 )=−8 ×−4=32
b)
g ( x )=x2−4 x−5

g ( 4 ) =42−4 ( 4 ) −5=−5
g ( 4 ) =−5
f ( x )=−x2 +6 x−9
f ( 4 )=−42 +6 ( 4 )−9=−1
f ( 4 )=−1
( g ° f ) ( 4 )=−5 ×−1=5
c)
g ( x )=x2−4 x−5
g (−2 )=(−2)2−4 (−2 )−5=7
g (−2 )=7
f ( x )=−x2 +6 x−9
f (−2 )=−(−2)2 +6 (−2 ) −9=−25
f ( −2 ) =−25
( f ° g ° g ) ( −2 ) =−25× 7 ×7=−1225
Q4)
y=(x2−1)
1
3
Let u=x2−1
du
dx =2 x
y=(u)
1
3
dy
du = 1
3 u
−2
3
dy
dx = dy
du . du
dx =(2 x) 1
3 u
−2
3

dy
dx = 2
3 xu
−2
3 = 2
3 x (x2−1)
−2
3
dy
dx = 2
3 (x2−1)
2
3
Let 3( x2−1)
2
3 =0
x2−1=0
x2=1
x=1∨−1
The largest set is (−1,1)
Q5)
3
√ 12=(12)
1
3
Let y=x
1
3
Where x=8 and ∆ x=4
dy
dx =1
3 x
−2
3 = 1
3 x
2
3
We also that ∆ y = dy
dx ∆ x
∆ y = 1
3 x
2
3
∆ x
∆ y = 1
3 ( 8 )
2
3
( 4)
∆ y = 1
3 (2)3 × 2
3
(4)
∆ y = 1
3 (2)2 (4 )
∆ y = 1
3 ( 4 ) ( 4 ) = 4
12 =0.3333

We have
∆ y =f ( x+ ∆ x)
1
3 −x
1
3
0.3333=(8+4)
1
3 −8
1
3
0.3333=(12)
1
3 −8
1
3
(12)
1
3 =0.3333+8
1
3
(12)
1
3 =0.3333+( 2)3 × 1
3
(12)
1
3 =0.3333+2=2.3333
3
√12=2.3333
Q6)
a)
The graph of function h has the following roots;
x=−3 ,−1,3,1
The equation of h can be obtained as shown below
h=(x +3)( x +1)( x−3)( x −1)
( x +3 ) ( x+1 ) =x2 + 4 x+ 3
( x−3 ) ( x−1 ) =x2−4 x +3
h=(x ¿¿ 2+4 x+3)(x ¿¿ 2−4 x +3)¿ ¿
h=x4−10 x2+ 9
F (x)=h ( x
2 )+ 1
F (x)=(x ¿¿ 4−10 x2+9)( x
2 )+1 ¿
F ( x )= 1
2 x5−5 x3+ 9
2 x+1
x -3 -2 -1 0 1 2 3

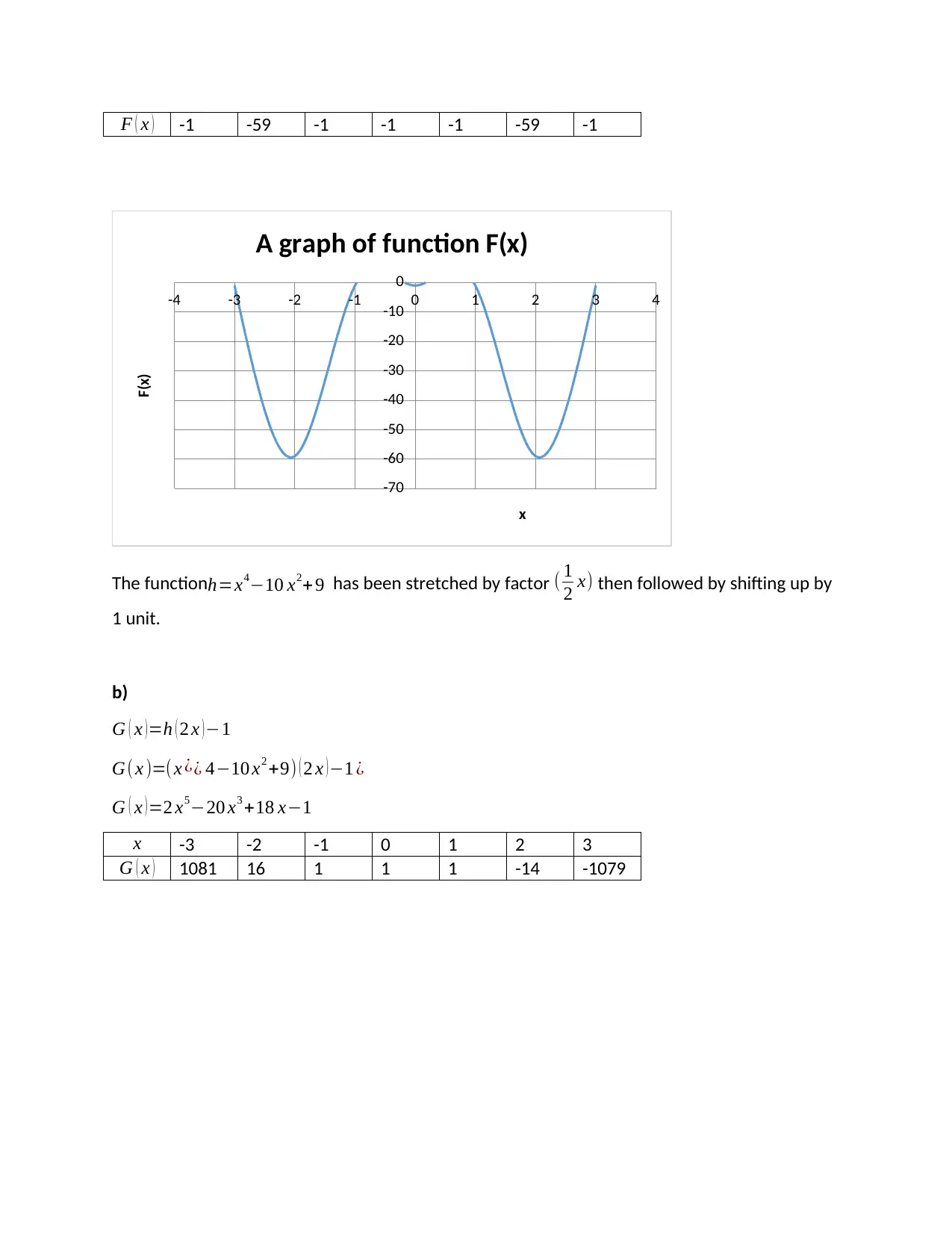
F ( x ) -1 -59 -1 -1 -1 -59 -1
-4 -3 -2 -1 0 1 2 3 4
-70
-60
-50
-40
-30
-20
-10
0
A graph of function F(x)
x
F(x)
The functionh=x4−10 x2+ 9 has been stretched by factor ( 1
2 x) then followed by shifting up by
1 unit.
b)
G ( x )=h ( 2 x )−1
G( x )=( x ¿¿ 4−10 x2 +9) ( 2 x ) −1 ¿
G ( x ) =2 x5−20 x3 +18 x−1
x -3 -2 -1 0 1 2 3
G ( x ) 1081 16 1 1 1 -14 -1079

-4 -3 -2 -1 0 1 2 3 4
-1500
-1000
-500
0
500
1000
1500
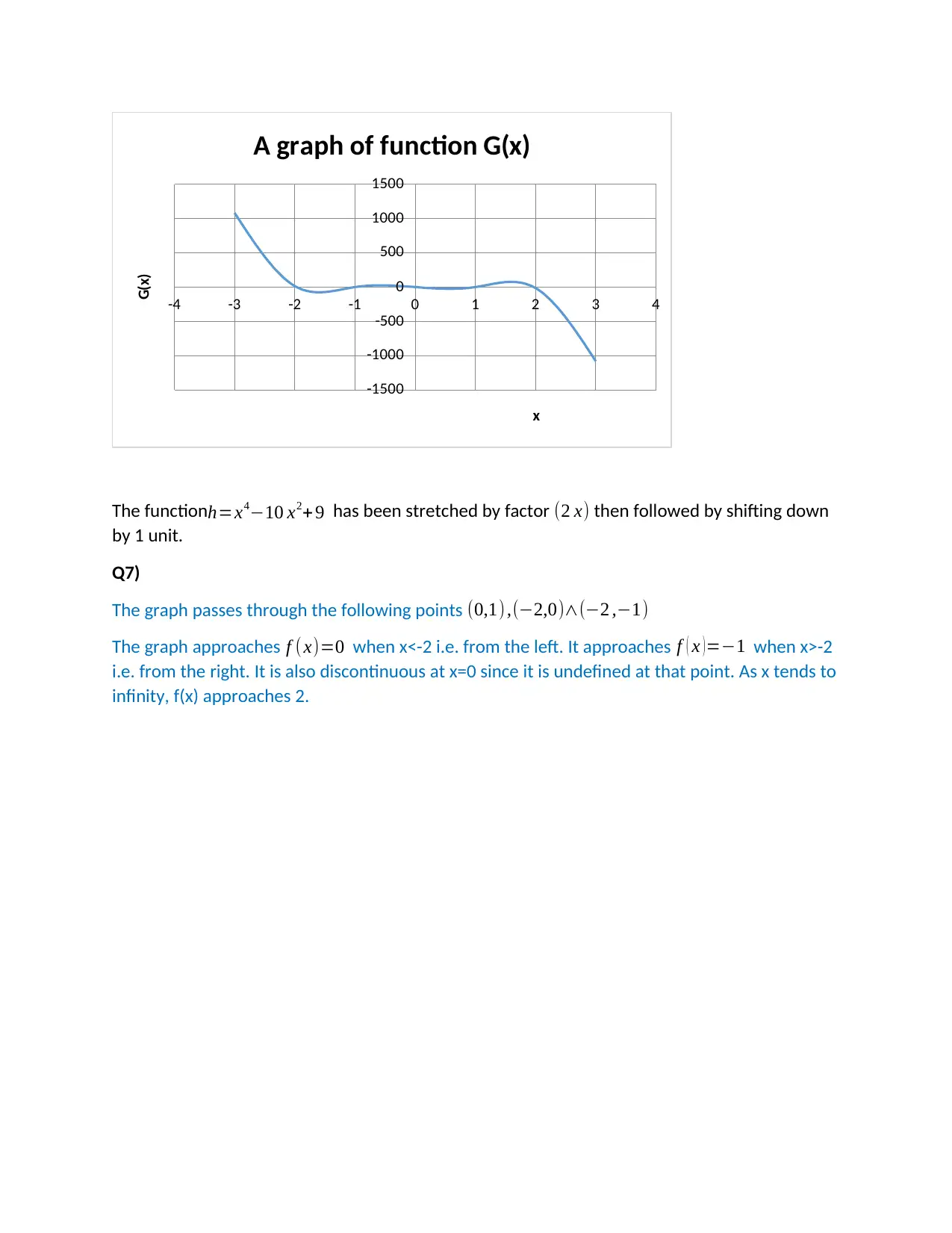
A graph of function G(x)
x
G(x)
The functionh=x4−10 x2+ 9 has been stretched by factor (2 x) then followed by shifting down
by 1 unit.
Q7)
The graph passes through the following points (0,1) ,(−2,0)∧(−2 ,−1)
The graph approaches f ( x)=0 when x<-2 i.e. from the left. It approaches f ( x )=−1 when x>-2
i.e. from the right. It is also discontinuous at x=0 since it is undefined at that point. As x tends to
infinity, f(x) approaches 2.

-3 -2 -1 0 1 2 3
-3
-2
-1
0
1
2
3
4
5
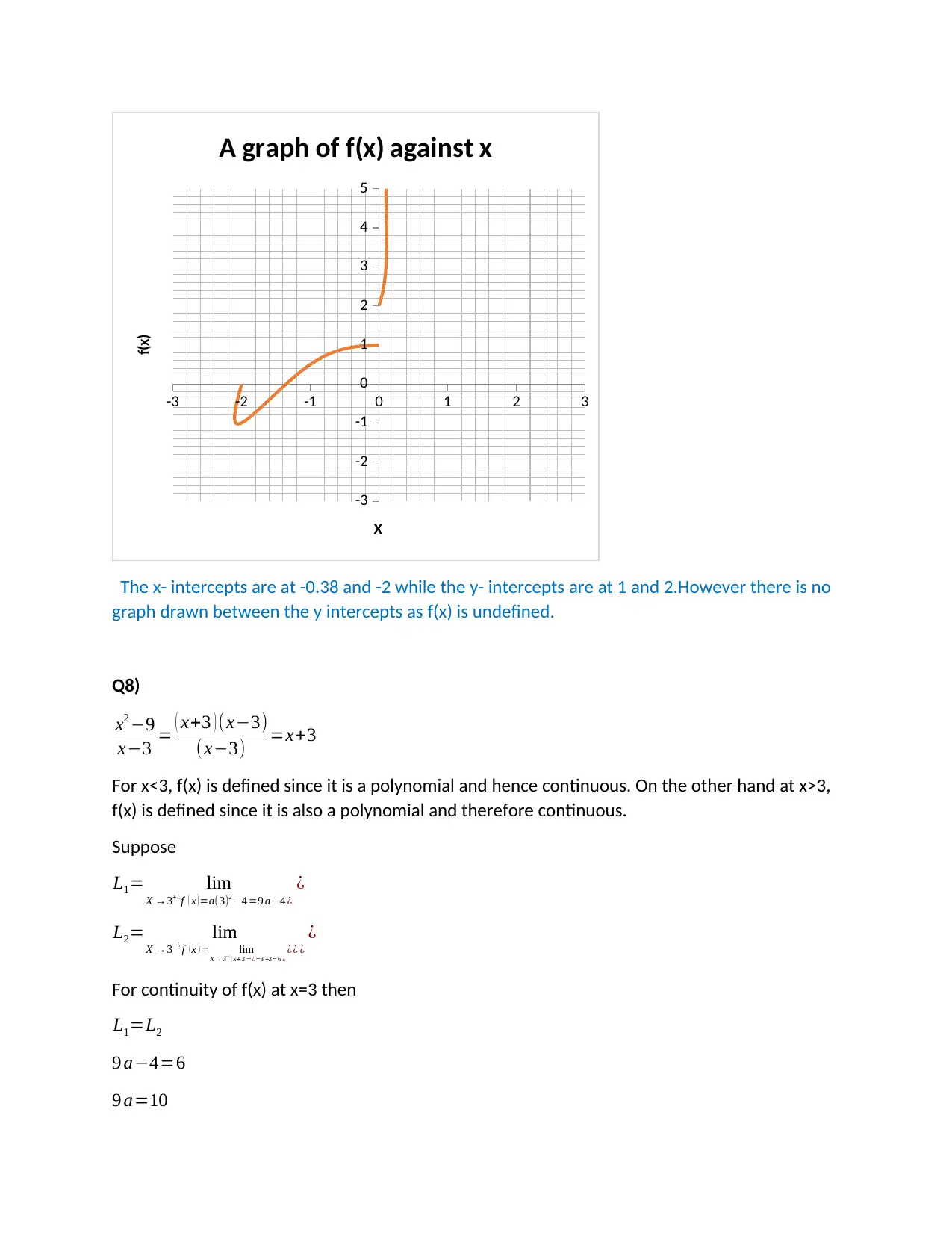
A graph of f(x) against x
X
f(x)
The x- intercepts are at -0.38 and -2 while the y- intercepts are at 1 and 2.However there is no
graph drawn between the y intercepts as f(x) is undefined.
Q8)
x2 −9
x−3 = ( x+3 ) (x−3)
(x−3) =x+3
For x<3, f(x) is defined since it is a polynomial and hence continuous. On the other hand at x>3,
f(x) is defined since it is also a polynomial and therefore continuous.
Suppose
L1= lim
X →3+ ¿f ( x ) =a(3)2−4 =9 a−4 ¿
¿
L2= lim
X →3−¿ f ( x ) = lim
X→ 3−¿ ( x+ 3 )=¿=3 +3=6 ¿
¿¿ ¿
¿
For continuity of f(x) at x=3 then
L1=L2
9 a−4=6
9 a=10

a= 10
9 =1 1
9
At x=3
f ( x)=b2
f ( 3 ) =b2 =0
b=0
Thus we have
f ( x )=
{ x2−9
x−3 , x <3
10
9 x2 , x >3
0 x=3
Q9)
a)
Using quotient law of limit we have
lim
x→ a ( f
g )=¿
lim
x→ a
f
lim
x→ a
f ¿
lim
x→ 0−¿
( sinx
g(x) )=¿ lim
x →0−¿ sinx
¿ lim
x→ 0−¿ g(x)
¿ sin 0
∞ = 0
∞ =0 ¿¿ ¿¿
¿
lim
x→ 0−¿
( sinx
g(x) )=0 ¿
¿
b)
lim
x→ 0+¿ g ( x ) tan (2 x)
tan(6 x) =¿¿ ¿
¿
= 4 × 0
0 =∞
There is no limit since we have 0 in the denominator hence making the function undefined.
c)

lim
x→ ∞ ( 1
g (x) )=
lim
x →∞
1
lim
x→ ∞
g(x )= 1
0 =∞
There is no limit since we have 0 in the denominator hence making the function undefined.
d)
lim
x →0 ( x−4
g(x ) ) =
lim
x→ ∞
x−4
lim
x →∞
g (x)= 0−4
4 =−4
4 =−1
Q10)
g( x )= x3−8
( x−2 ) (x2−x−12)
Let x=2
As x approaches 2, the denominator and the numerator both approach 0.
If x>2 , g(x )>0 Thus lim
x→ 2+¿ g ( x ) =∞ ¿
¿
If x<2 , g(x )<0 Thus lim
x→ 2−¿ g ( x ) =−∞ ¿
¿
Therefore x=2 is a vertical asymptote.
Let x=4
As x approaches 4, the denominator approaches 0.
If x>4 , g(x )>0 Thus lim
x→ 4+ ¿ g ( x ) =∞ ¿
¿
If x<4 , g(x )<0 Thus lim
x→ 4−¿ g ( x )=−∞ ¿
¿
Therefore x=4 is a vertical asymptote.
Let x=-3
As x approaches -3, the denominator approaches 0.
If x>−3 , g ( x)>0 Thus lim
x→−3+ ¿ g (x )=∞ ¿
¿
If x ←3 , g( x )>0 Thus lim
x→−3−¿ g ( x )=∞ ¿
¿

Therefore x=-3 is a vertical asymptote.
Q11)
The lines that are parallel have equal gradient.
y− √2 x=3
y= √2 x+ 3
The gradient of the parallel line is √2 and hence the tangent line will have the same gradient.
When x=a=−π
2
cos (2 x )=cos (2 a)=cos (-π ¿=−1
The tangent passes through the point ( −π
2 ,−1 ¿
((a , f (a) ¿=(a , cos (2 a))
Using the points ( −π
2 ,−1 ¿ and (a , cos (2 a)¿ having a gradient of √2
cos(2a)+1
a+ π
2
= √ 2
cos (2 a)+ 1= √2 (a+ π
2 )
cos (2 a)+1= √ 2 a+ √ 2
2 π
cos (2 a)= √2 a+ √ 2
2 π−1 ……………………………….i
When x=a= π
3
cos (2 x )=cos (2 a)=cos ( 2
3 π ¿=−1
2
The tangent passes through the point ( π
3 ,− 1
2 ¿
Using the points ( π
3 ,− 1
2 ) and (a , cos (2 a)¿ having a gradient of √ 2

cos( 2a)+ 1
2
a− π
3
= √ 2
cos (2 a)+ 1
2 = √2 (a− π
3 )
cos ( 2 a )+ ¿ 1
2 = √2 a− √ 2
3 π ¿
cos ( 2 a )= √2 a− √ 2
3 π −1
2 ……………………………….ii
Comparing i and ii we have
cos (2 a)= √ 2 a+ √ 2
2 π−1= √ 2 a− √ 2
3 π −1
2
cos (2 a)= √ 2
2 π −1=−√ 2
3 π −1
2
cos (2 a)= √ 2
2 π + √ 2
3 π −1+1
2 =0
cos (2 a)= √ 2
2 π + √ 2
3 π −1+1
2 =0
cos (2 a)= 5 √ 2
6 π− 1
2 =0
cos (2 a)= 5 √ 2
6 π− 1
2
cos (2 a)=0
Ignoring cos( 2a)=5 √ 2
6 π − 1
2 and using
cos (2 a)=0
cos (2 a)=cos ( π
2 ,− π
2 )
2 a= π
2 ,− π
2
a= π
4 ,− π
4

a= π
4 Or
a=−π
4
Q12)
a)
d
dx √sec ( 2 x )
We shall apply the chain rule
df (u)
dx = df
du . du
dx
Let f =√u and u=sec (2 x)
d
dx √sec ( 2 x )= d
dx ( √ u ) d
dx ( sec(2 x) )
¿ 1
2 √ u ( sec ( 2 x ) tan ( 2 x ) .2 )
¿ 1
2 √ sec (2 x ) ( sec ( 2 x ) tan ( 2 x ) .2 )
b)
d
dx ( sin x
x−3 x
2
3 )
We shall apply the Quotient rule
( f
g )'
= f ' . g−g' . f
g2
d
dx ( sin x
x−3 x
2
3 )=
d
dx ( sinx ¿ ) ( x−3 x
2
3 )− d
dx ( x−3 x
2
3 ) ( sinx ¿ )
( x−3 x
2
3 )2
=
( cosx¿ ) ( x−3 x
2
3 )−
(1− 2
x
1
3 ) ( sinx ¿ )
( x−3 x
2
3 )2

c)
d2
d x2 ( x3 tan x )
We shall apply the product rule
d
dx ( x3 tan x ) =3 x2 tan (x)+ sec2 ( x) x3
d
dx (3 x2 tan ( x ) + sec2 ( x ) x3 )
=2 x3 sec2 ( x ) tan ( x )+6 x2 sec2 ( x )+6 xtan( x )
Q13)
v h
45°
x
Let v ¿ represent speed of aircraft ∈the direction shown above while x∧h
horizontal∧vertical component of the speed of the aircraft respectively .
sin 45 °= h
v
h=v (sin 45 °)
v=500 mi /h
h=500(sin 45 ° )
√ 2 1

45°
1
( sin 45 ° ) = 1
√2
h=500(sin 45 ° )
h=500 ( 1
√ 2 )= 500
√2
h=500 ( 1
√ 2 )= 500
√2
Rationalizing the denominator we get
h=500
√2 × √2
√2 = 500 √ 2
2 =250 √2
The aircraft is gaining altitude at 250 √2mi /h