Interpretation of Regression Analysis Results

This assignment involves interpreting the results of a regression analysis performed on a dataset related to sports. The output includes various tables and summaries, which are then analyzed to understand the relationship between different variables such as 'OVERRUN', 'BOXER', 'ROUND', 'WT', and 'HOUSE'. The interpretation focuses on identifying statistically significant differences in mean values for certain variables, indicating that there is no significant difference in the mean values of power and other independent variables. The assignment also references various sources and provides a summary of the analysis performed.

SPSS

TABLE OF CONTENTS
12.2...................................................................................................................................................4
A ANOVA table..........................................................................................................................4
B. Number of treatments are involved in experiment..................................................................4
C. Implicating the sufficient evidence to indicates a difference among the treatment a= .10.....4
12. 4..................................................................................................................................................4
A. Applicating MST.....................................................................................................................5
b. Measuring MSE.......................................................................................................................5
C. df in MST................................................................................................................................5
D. df in MSE................................................................................................................................6
E. Statistical analysis...................................................................................................................6
F. Summary..................................................................................................................................7
G. Specification............................................................................................................................7
H. Conclusion..............................................................................................................................7
12.12.................................................................................................................................................7
A. Implication of experimental technique to be used in analyzing the outcomes.......................7
B. Analyzing the means of variables...........................................................................................8
C Assumptions.............................................................................................................................8
12.14.................................................................................................................................................9
A. Identification of the treatment to be followed.........................................................................9
B Conducting the analysis over variance on data and interpretation of outcomes......................9
12.22.................................................................................................................................................9
A comparison of hypothesis.........................................................................................................9
B. Representing ANOVA table....................................................................................................9

C. SAS measurements................................................................................................................10
12.24...............................................................................................................................................12
12.26...............................................................................................................................................13
Regression .................................................................................................................................13
A Constructing and ANOVA summary table............................................................................13
B. Punching power means..........................................................................................................14
C. Removing an unwanted source of variable...........................................................................14
12.36...............................................................................................................................................15
A. Identification of varaious factors and treatments..................................................................16
B. Conducting research through ANOVA table........................................................................16
Regression..................................................................................................................................16
C. Evidences for interaction between Housing system and Weight class.................................17
REFERENCES..............................................................................................................................19

12.2
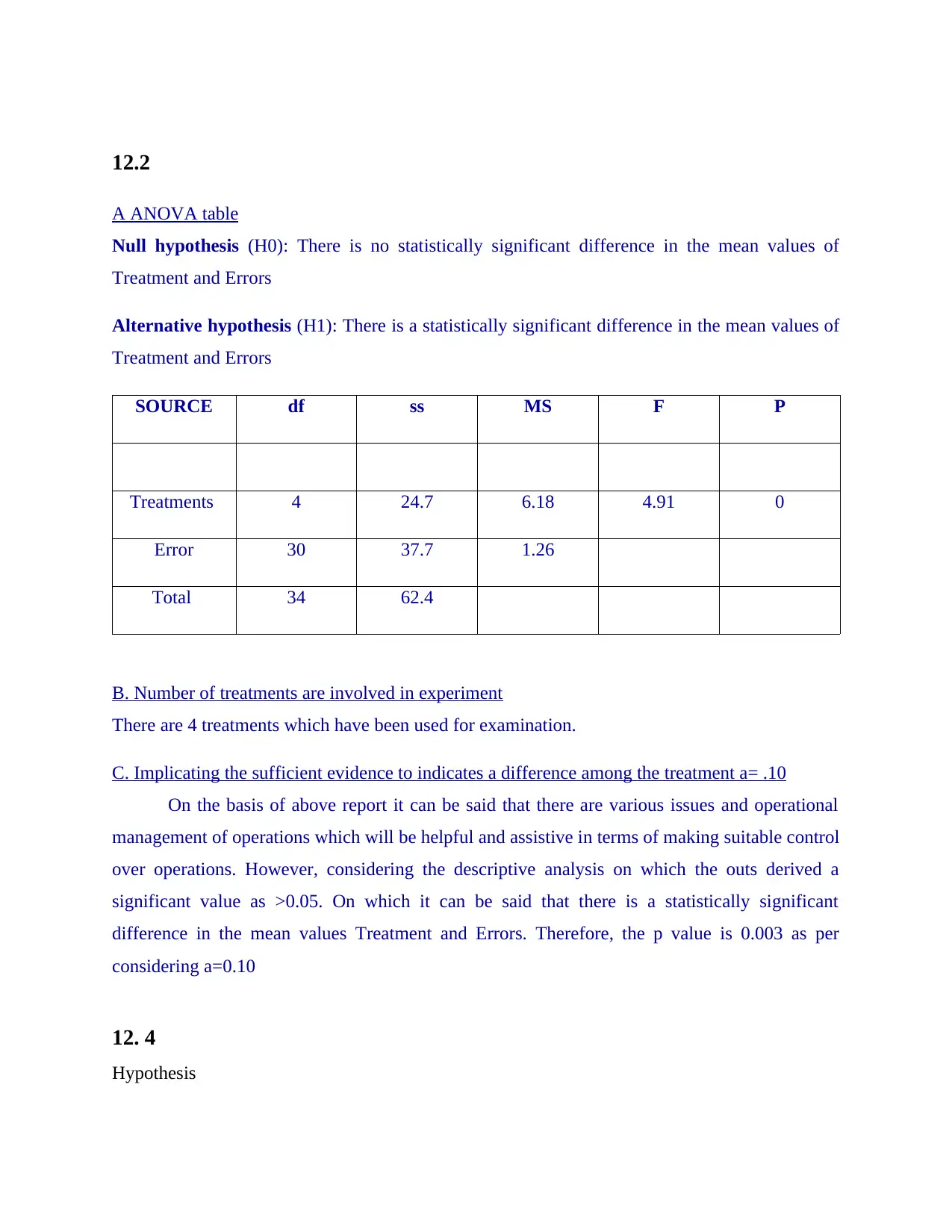
A ANOVA table
Null hypothesis (H0): There is no statistically significant difference in the mean values of
Treatment and Errors
Alternative hypothesis (H1): There is a statistically significant difference in the mean values of
Treatment and Errors
SOURCE df ss MS F P
Treatments 4 24.7 6.18 4.91 0
Error 30 37.7 1.26
Total 34 62.4
B. Number of treatments are involved in experiment
There are 4 treatments which have been used for examination.
C. Implicating the sufficient evidence to indicates a difference among the treatment a= .10
On the basis of above report it can be said that there are various issues and operational
management of operations which will be helpful and assistive in terms of making suitable control
over operations. However, considering the descriptive analysis on which the outs derived a
significant value as >0.05. On which it can be said that there is a statistically significant
difference in the mean values Treatment and Errors. Therefore, the p value is 0.003 as per
considering a=0.10
12. 4
Hypothesis

Null hypothesis (H0): There is no statistically significant difference in the mean values of
dependent variable responses and factor variable treatment.
Alternative hypothesis (H1): There is a statistically significant difference in the mean values of
dependent variable responses and factor variable treatment.
A. Applicating MST
SST= Sum square of treatment
=Total sum of square – Correction for mean
= 26.190- 7.502
=18.688
SSE= Sum square of error
=SST-SS
=18.88-26.190
=-7.502
MST= Mean Square for treatments
=SST
P-1
=18.688
0.05-1
= -19.67
b. Measuring MSE
MSE= Mean square for error
=SSE
n-p
-7.502 = -1.079
7-0.05

C. df in MST
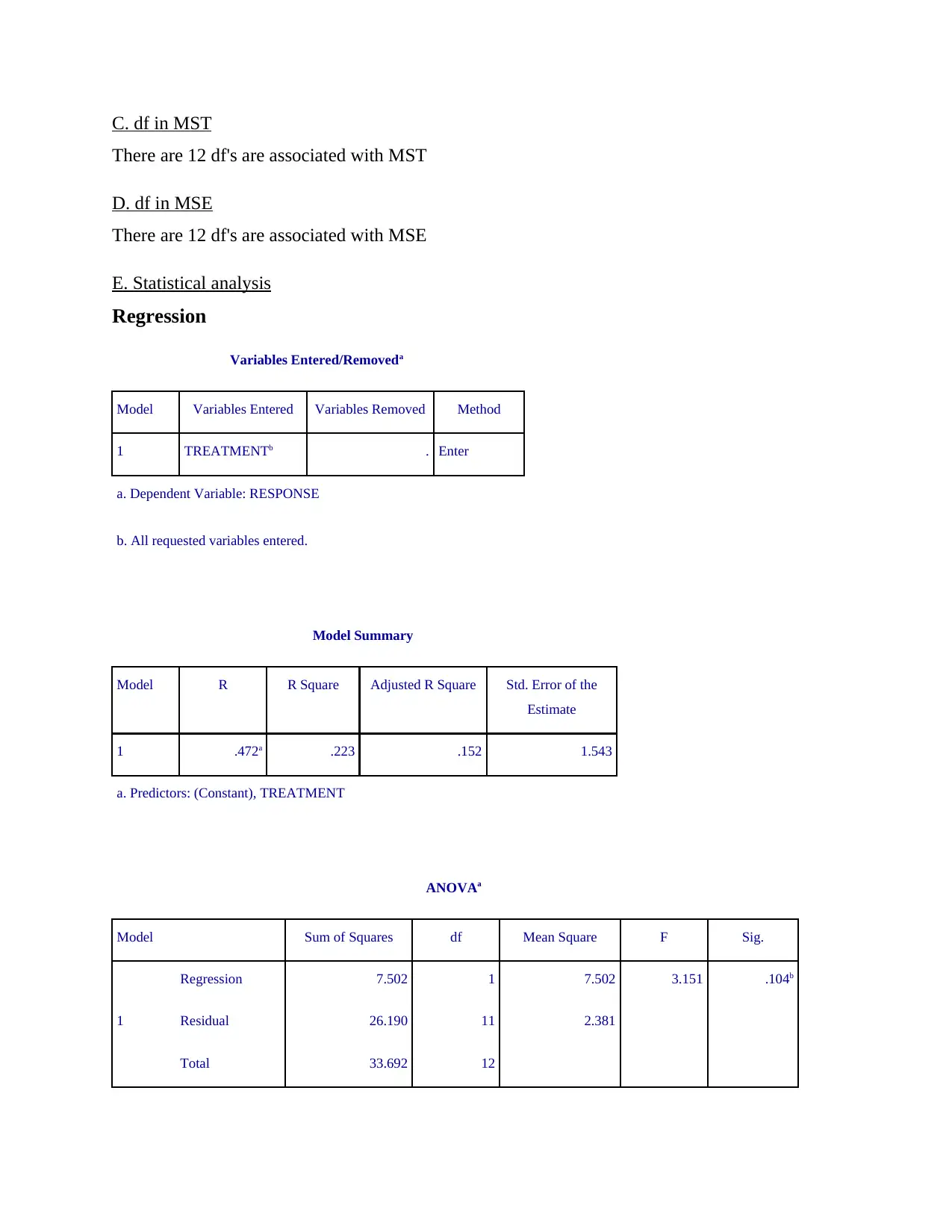
There are 12 df's are associated with MST
D. df in MSE
There are 12 df's are associated with MSE
E. Statistical analysis
Regression
Variables Entered/Removeda
Model Variables Entered Variables Removed Method
1 TREATMENTb . Enter
a. Dependent Variable: RESPONSE
b. All requested variables entered.
Model Summary
Model R R Square Adjusted R Square Std. Error of the
Estimate
1 .472a .223 .152 1.543
a. Predictors: (Constant), TREATMENT
ANOVAa
Model Sum of Squares df Mean Square F Sig.
1
Regression 7.502 1 7.502 3.151 .104b
Residual 26.190 11 2.381
Total 33.692 12

a. Dependent Variable: RESPONSE
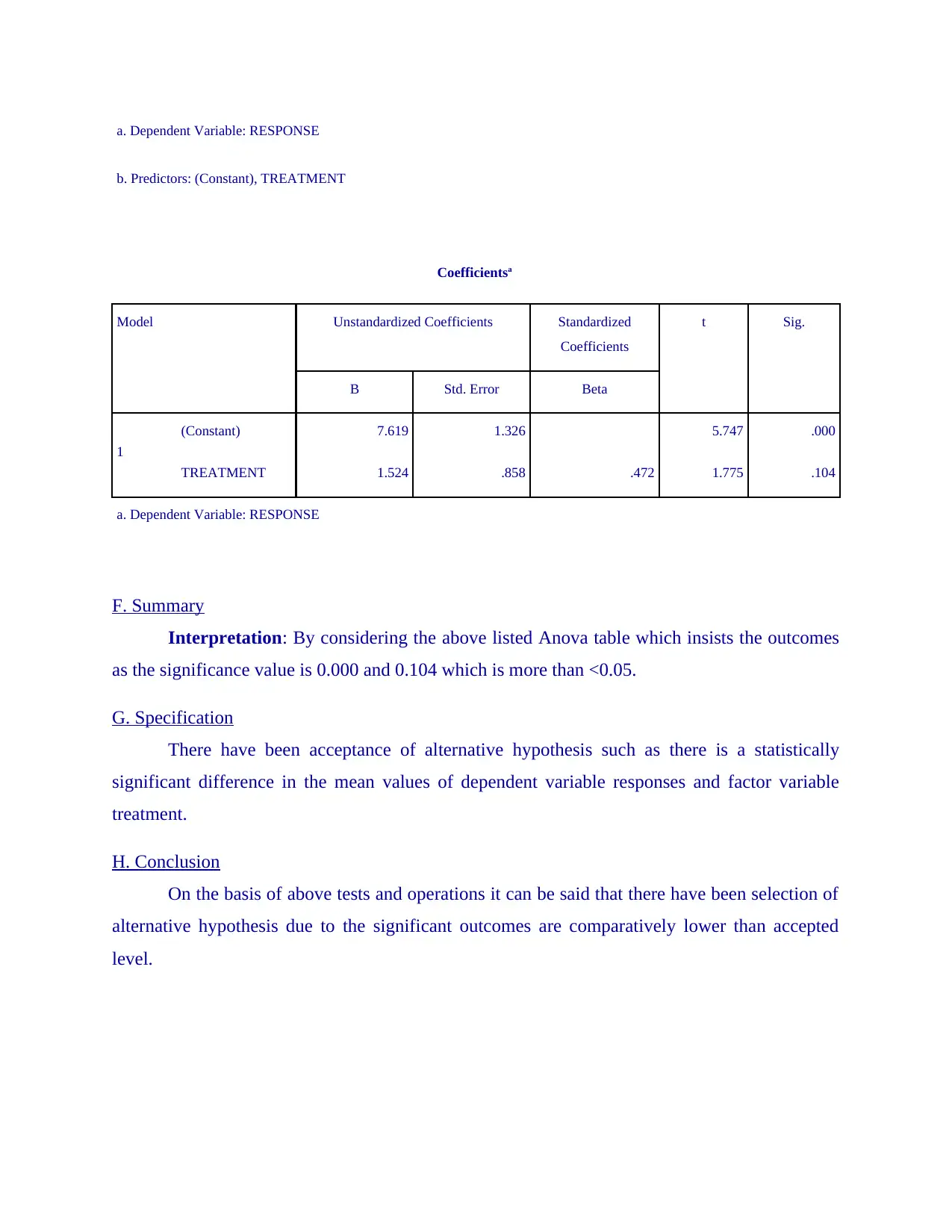
b. Predictors: (Constant), TREATMENT
Coefficientsa
Model Unstandardized Coefficients Standardized
Coefficients
t Sig.
B Std. Error Beta
1
(Constant) 7.619 1.326 5.747 .000
TREATMENT 1.524 .858 .472 1.775 .104
a. Dependent Variable: RESPONSE
F. Summary
Interpretation: By considering the above listed Anova table which insists the outcomes
as the significance value is 0.000 and 0.104 which is more than <0.05.
G. Specification
There have been acceptance of alternative hypothesis such as there is a statistically
significant difference in the mean values of dependent variable responses and factor variable
treatment.
H. Conclusion
On the basis of above tests and operations it can be said that there have been selection of
alternative hypothesis due to the significant outcomes are comparatively lower than accepted
level.

12.12
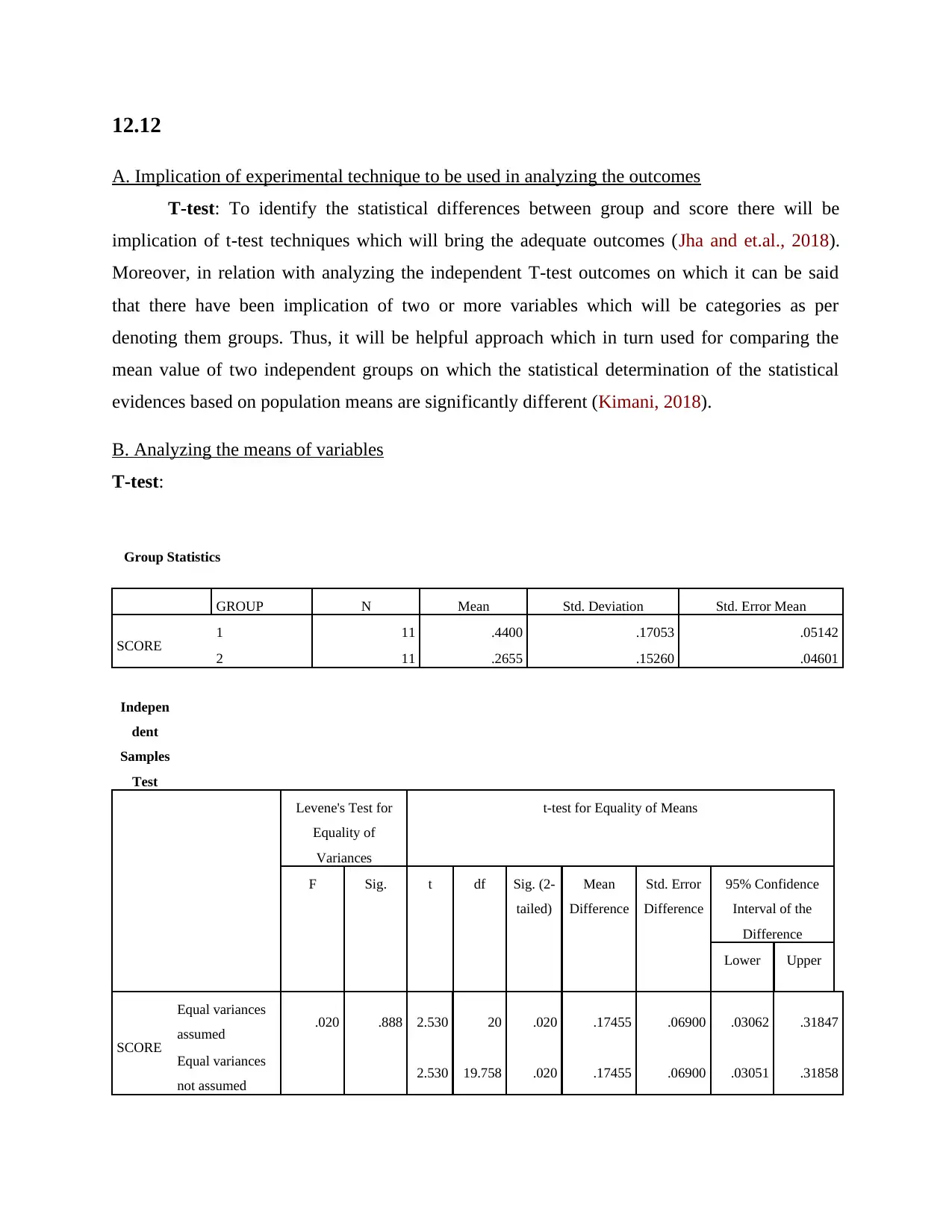
A. Implication of experimental technique to be used in analyzing the outcomes
T-test: To identify the statistical differences between group and score there will be
implication of t-test techniques which will bring the adequate outcomes (Jha and et.al., 2018).
Moreover, in relation with analyzing the independent T-test outcomes on which it can be said
that there have been implication of two or more variables which will be categories as per
denoting them groups. Thus, it will be helpful approach which in turn used for comparing the
mean value of two independent groups on which the statistical determination of the statistical
evidences based on population means are significantly different (Kimani, 2018).
B. Analyzing the means of variables
T-test:
Group Statistics
GROUP N Mean Std. Deviation Std. Error Mean
SCORE 1 11 .4400 .17053 .05142
2 11 .2655 .15260 .04601
Indepen
dent
Samples
Test
Levene's Test for
Equality of
Variances
t-test for Equality of Means
F Sig. t df Sig. (2-
tailed)
Mean
Difference
Std. Error
Difference
95% Confidence
Interval of the
Difference
Lower Upper
SCORE
Equal variances
assumed .020 .888 2.530 20 .020 .17455 .06900 .03062 .31847
Equal variances
not assumed 2.530 19.758 .020 .17455 .06900 .03051 .31858

C Assumptions
Interpretation: By considering the above listed table it can be said that there have been
consideration over the score and group. The significant value is less than 0.05 on which it can be
said that the alternative hypothesis will be selected as there will be a significant statistical
relationship between group and score.
12.14
A. Identification of the treatment to be followed.
In relation with ascertaining the outcomes there have been use of various outcomes. In
relation with analyzing the outcomes as considering population there is needed to have adequate
determination of the facts (Annotated output, 2018). Thus, considering descriptive analysis, one
way ANOVAs and various techniques which will be helpful in determining outcomes (Kimani,
Waititu and Iravo, 2017).
B Conducting the analysis over variance on data and interpretation of outcomes
12.22
A comparison of hypothesis
One way ANOVA
Null hypothesis (H0): There is no statistically significant difference in the mean values of
dependent variable GROUP and other independent variable SOCRE.
Alternative hypothesis (H1): There is a statistically significant difference in the mean values of
variable GROUP and other independent variable SOCRE.
B. Representing ANOVA table
ANOVA
GROUP

Sum of Squares df Mean Square F Sig.
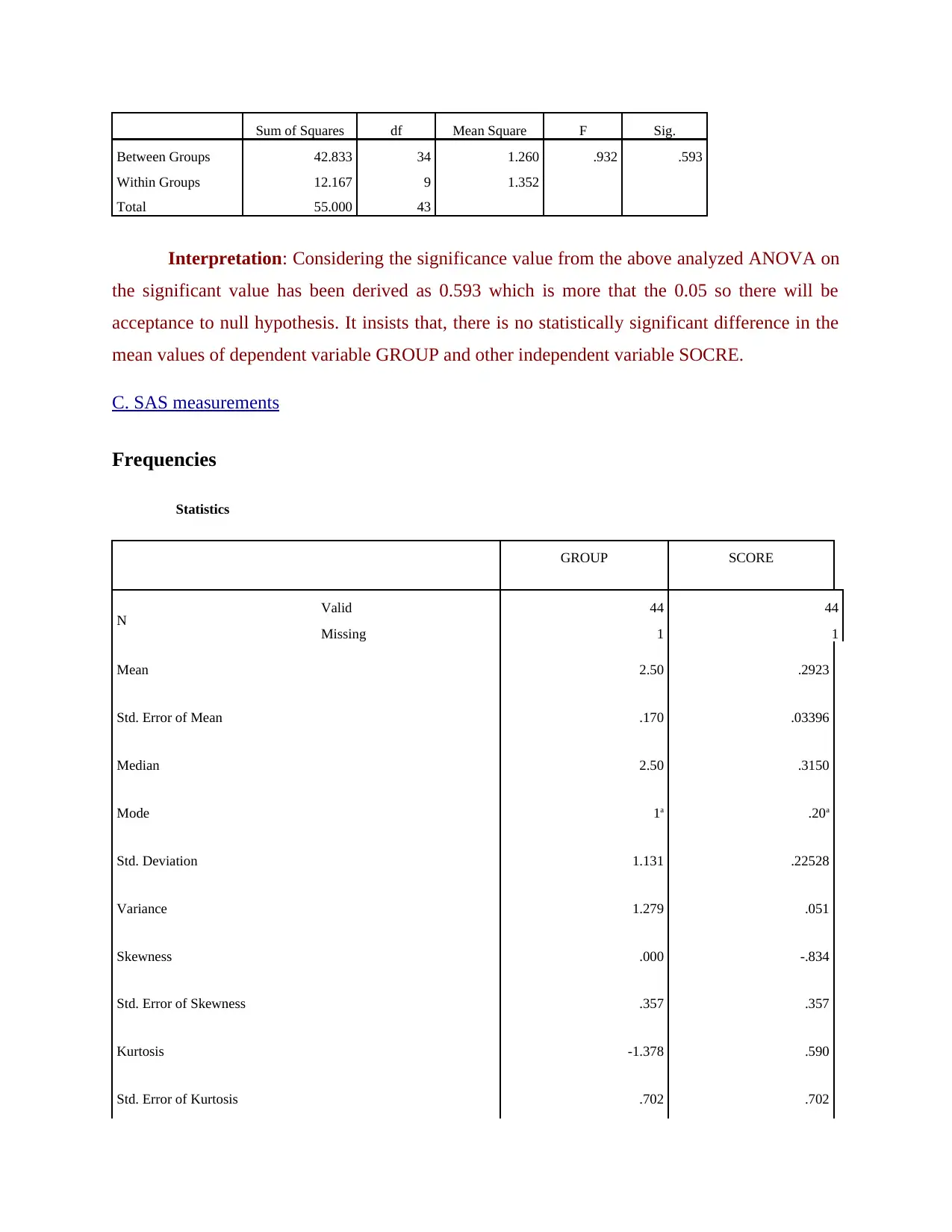
Between Groups 42.833 34 1.260 .932 .593
Within Groups 12.167 9 1.352
Total 55.000 43
Interpretation: Considering the significance value from the above analyzed ANOVA on
the significant value has been derived as 0.593 which is more that the 0.05 so there will be
acceptance to null hypothesis. It insists that, there is no statistically significant difference in the
mean values of dependent variable GROUP and other independent variable SOCRE.
C. SAS measurements
Frequencies
Statistics
GROUP SCORE
N Valid 44 44
Missing 1 1
Mean 2.50 .2923
Std. Error of Mean .170 .03396
Median 2.50 .3150
Mode 1a .20a
Std. Deviation 1.131 .22528
Variance 1.279 .051
Skewness .000 -.834
Std. Error of Skewness .357 .357
Kurtosis -1.378 .590
Std. Error of Kurtosis .702 .702

Range 3 .97
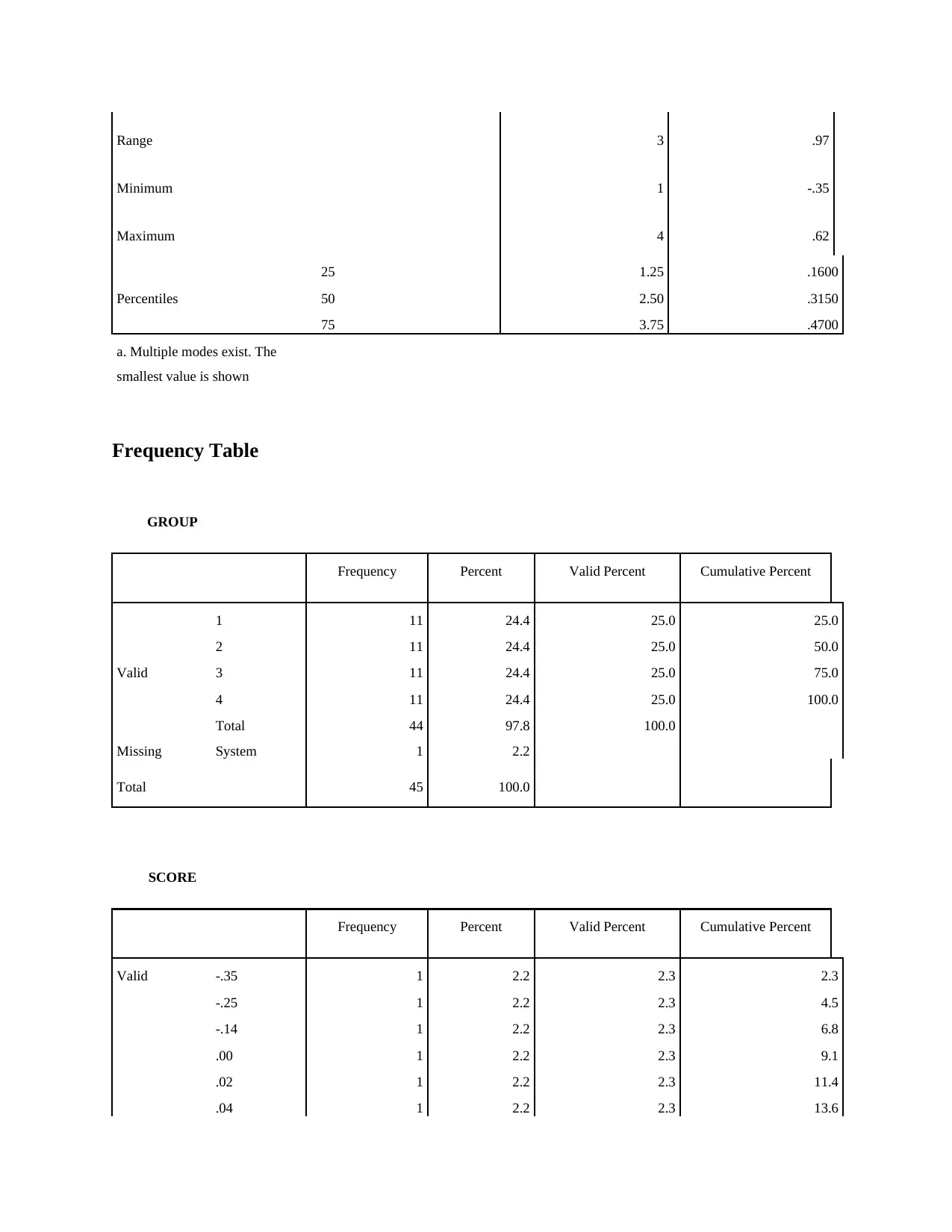
Minimum 1 -.35
Maximum 4 .62
Percentiles
25 1.25 .1600
50 2.50 .3150
75 3.75 .4700
a. Multiple modes exist. The
smallest value is shown
Frequency Table
GROUP
Frequency Percent Valid Percent Cumulative Percent
Valid
1 11 24.4 25.0 25.0
2 11 24.4 25.0 50.0
3 11 24.4 25.0 75.0
4 11 24.4 25.0 100.0
Total 44 97.8 100.0
Missing System 1 2.2
Total 45 100.0
SCORE
Frequency Percent Valid Percent Cumulative Percent
Valid -.35 1 2.2 2.3 2.3
-.25 1 2.2 2.3 4.5
-.14 1 2.2 2.3 6.8
.00 1 2.2 2.3 9.1
.02 1 2.2 2.3 11.4
.04 1 2.2 2.3 13.6

.10 2 4.4 4.5 18.2
.12 1 2.2 2.3 20.5
.15 1 2.2 2.3 22.7
.16 2 4.4 4.5 27.3
.18 1 2.2 2.3 29.5
.20 3 6.7 6.8 36.4
.21 1 2.2 2.3 38.6
.22 1 2.2 2.3 40.9
.26 1 2.2 2.3 43.2
.29 1 2.2 2.3 45.5
.30 1 2.2 2.3 47.7
.31 1 2.2 2.3 50.0
.32 1 2.2 2.3 52.3
.34 1 2.2 2.3 54.5
.36 1 2.2 2.3 56.8
.39 1 2.2 2.3 59.1
.40 1 2.2 2.3 61.4
.42 1 2.2 2.3 63.6
.43 2 4.4 4.5 68.2
.44 1 2.2 2.3 70.5
.46 1 2.2 2.3 72.7
.47 2 4.4 4.5 77.3
.50 3 6.7 6.8 84.1
.51 1 2.2 2.3 86.4
.52 1 2.2 2.3 88.6
.53 1 2.2 2.3 90.9
.58 2 4.4 4.5 95.5
.61 1 2.2 2.3 97.7
.62 1 2.2 2.3 100.0
Total 44 97.8 100.0
Missing System 1 2.2
Total 45 100.0
Descriptive
Statistics

N Minimum Maximum Mean Std. Deviation
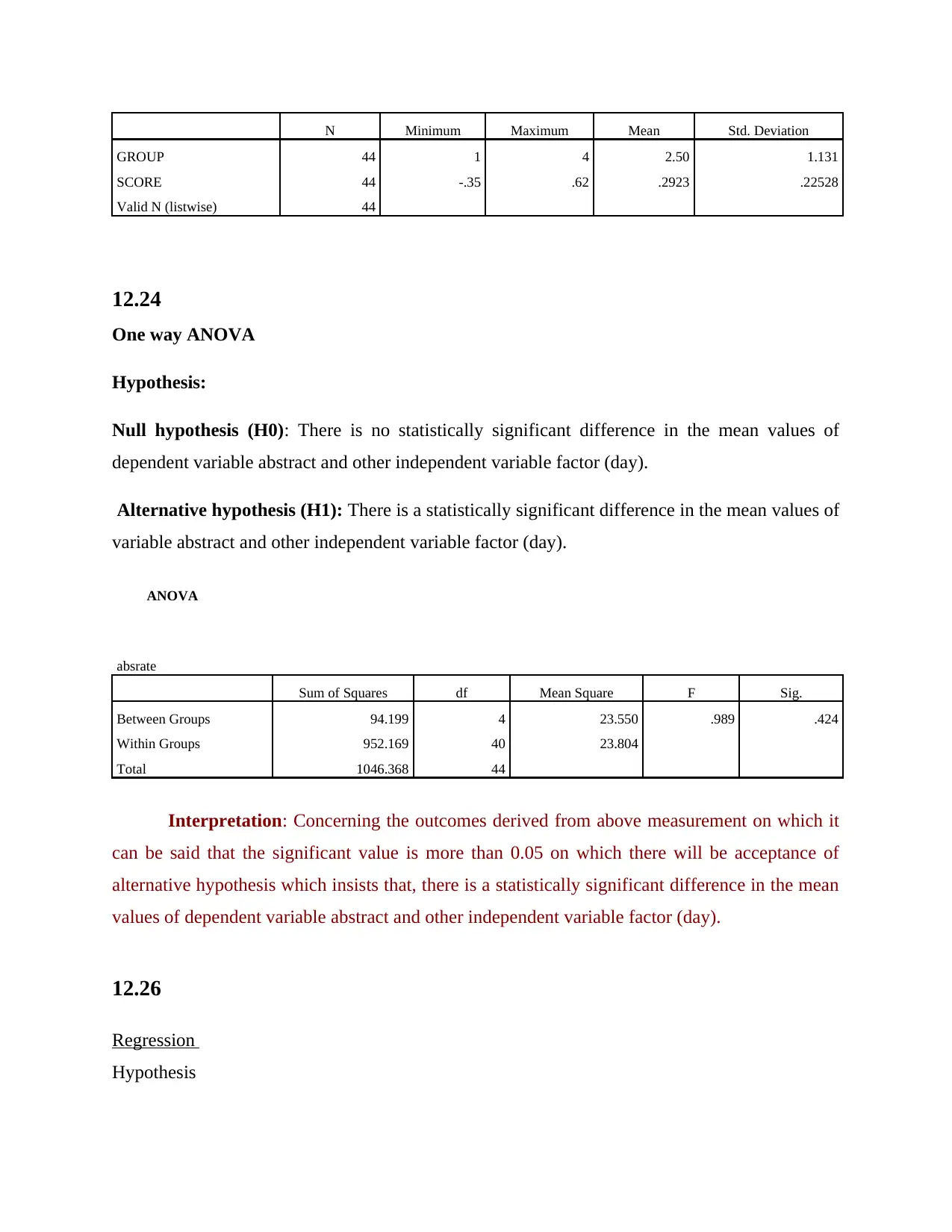
GROUP 44 1 4 2.50 1.131
SCORE 44 -.35 .62 .2923 .22528
Valid N (listwise) 44
12.24
One way ANOVA
Hypothesis:
Null hypothesis (H0): There is no statistically significant difference in the mean values of
dependent variable abstract and other independent variable factor (day).
Alternative hypothesis (H1): There is a statistically significant difference in the mean values of
variable abstract and other independent variable factor (day).
ANOVA
absrate
Sum of Squares df Mean Square F Sig.
Between Groups 94.199 4 23.550 .989 .424
Within Groups 952.169 40 23.804
Total 1046.368 44
Interpretation: Concerning the outcomes derived from above measurement on which it
can be said that the significant value is more than 0.05 on which there will be acceptance of
alternative hypothesis which insists that, there is a statistically significant difference in the mean
values of dependent variable abstract and other independent variable factor (day).
12.26
Regression
Hypothesis

Null hypothesis (H0): There is no statistically significant difference in the mean values of power
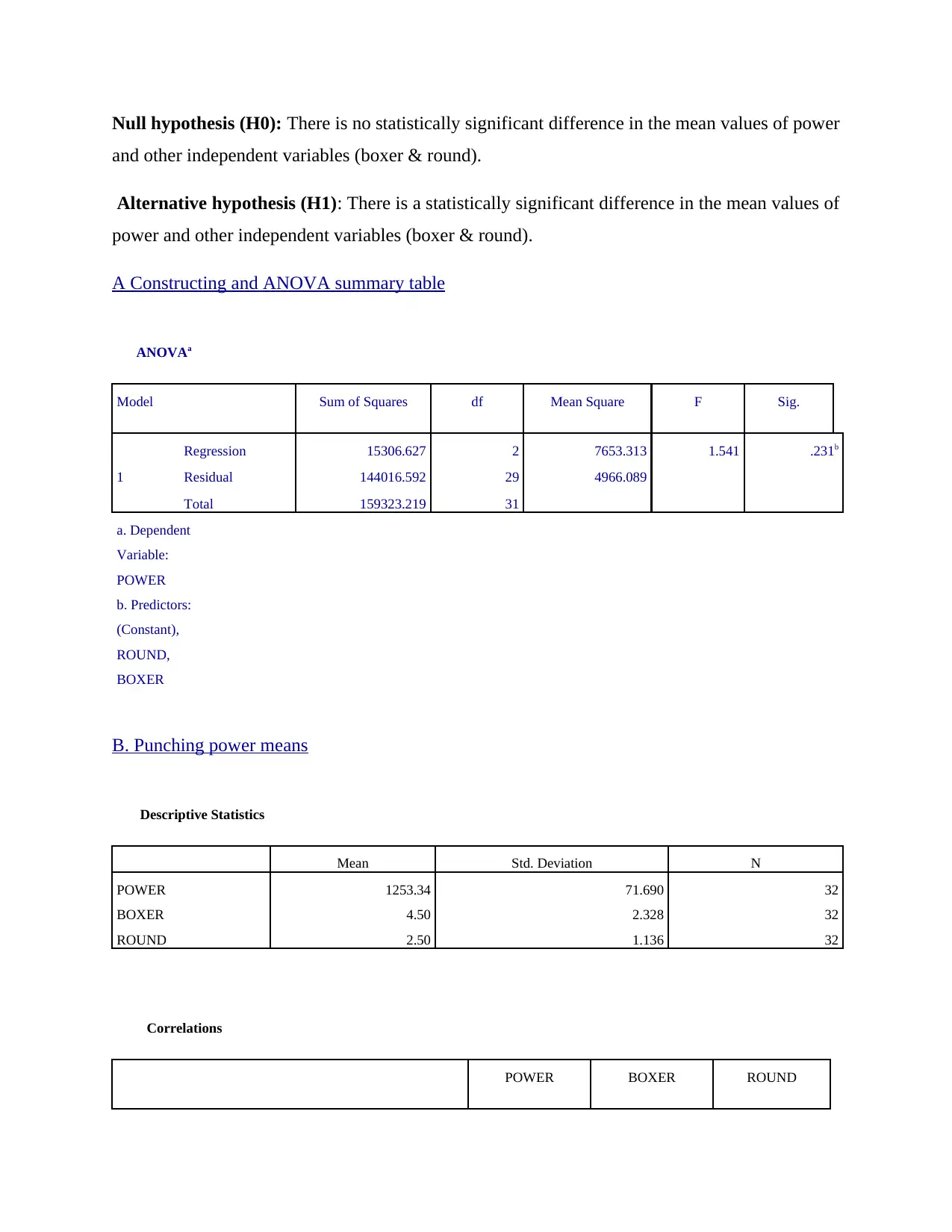
and other independent variables (boxer & round).
Alternative hypothesis (H1): There is a statistically significant difference in the mean values of
power and other independent variables (boxer & round).
A Constructing and ANOVA summary table
ANOVAa
Model Sum of Squares df Mean Square F Sig.
1
Regression 15306.627 2 7653.313 1.541 .231b
Residual 144016.592 29 4966.089
Total 159323.219 31
a. Dependent
Variable:
POWER
b. Predictors:
(Constant),
ROUND,
BOXER
B. Punching power means
Descriptive Statistics
Mean Std. Deviation N
POWER 1253.34 71.690 32
BOXER 4.50 2.328 32
ROUND 2.50 1.136 32
Correlations
POWER BOXER ROUND

Pearson Correlation
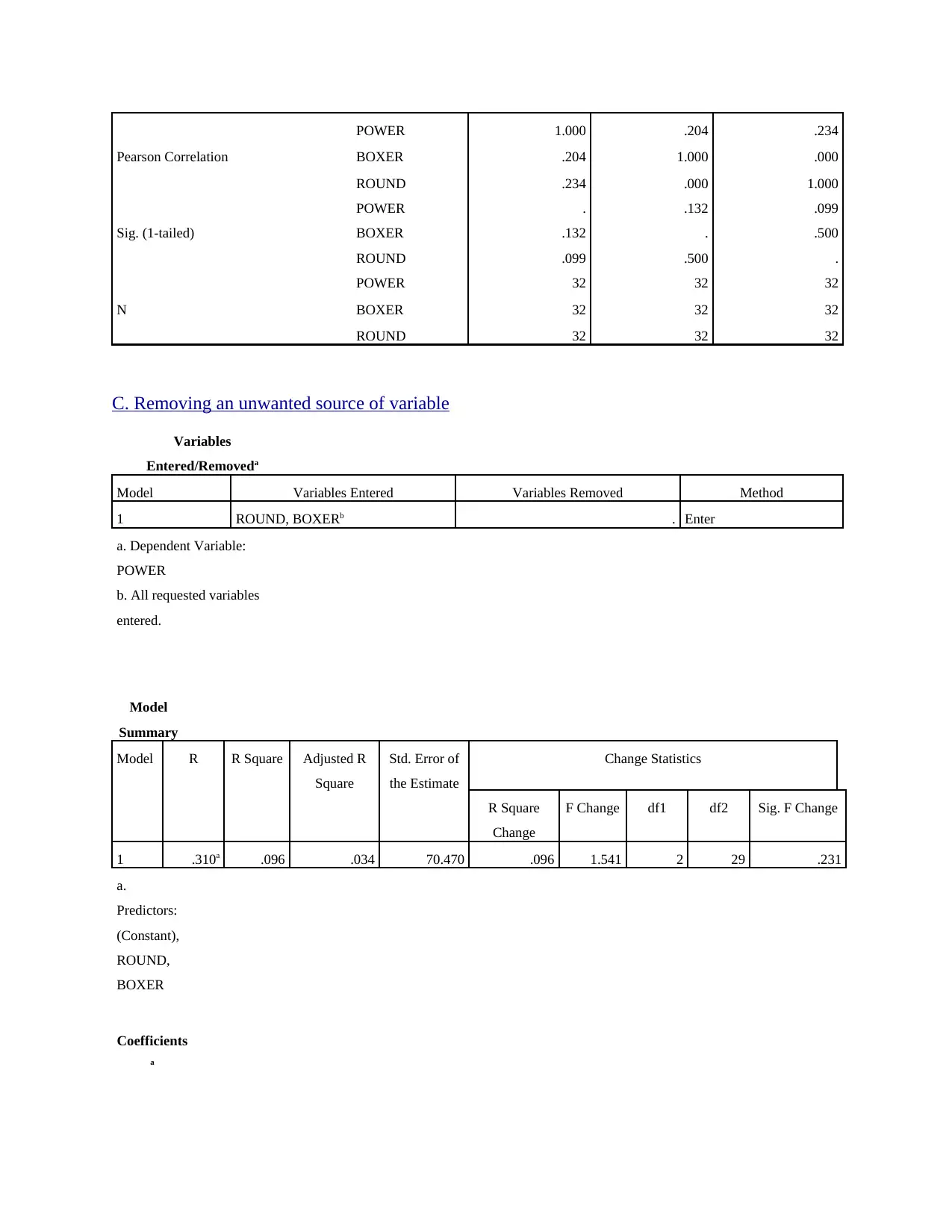
POWER 1.000 .204 .234
BOXER .204 1.000 .000
ROUND .234 .000 1.000
Sig. (1-tailed)
POWER . .132 .099
BOXER .132 . .500
ROUND .099 .500 .
N
POWER 32 32 32
BOXER 32 32 32
ROUND 32 32 32
C. Removing an unwanted source of variable
Variables
Entered/Removeda
Model Variables Entered Variables Removed Method
1 ROUND, BOXERb . Enter
a. Dependent Variable:
POWER
b. All requested variables
entered.
Model
Summary
Model R R Square Adjusted R
Square
Std. Error of
the Estimate
Change Statistics
R Square
Change
F Change df1 df2 Sig. F Change
1 .310a .096 .034 70.470 .096 1.541 2 29 .231
a.
Predictors:
(Constant),
ROUND,
BOXER
Coefficients
a

Model Unstandardized Coefficients Standardized
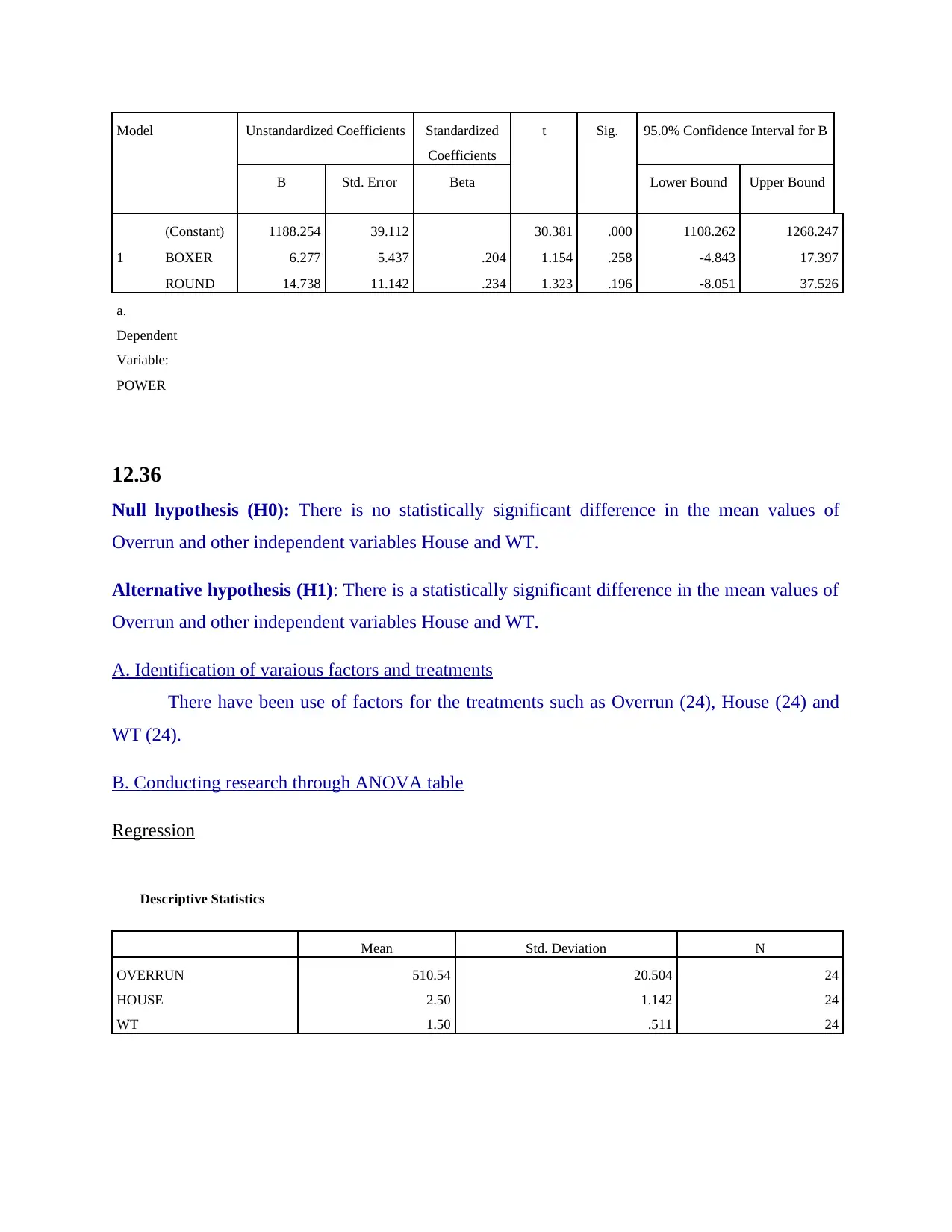
Coefficients
t Sig. 95.0% Confidence Interval for B
B Std. Error Beta Lower Bound Upper Bound
1
(Constant) 1188.254 39.112 30.381 .000 1108.262 1268.247
BOXER 6.277 5.437 .204 1.154 .258 -4.843 17.397
ROUND 14.738 11.142 .234 1.323 .196 -8.051 37.526
a.
Dependent
Variable:
POWER
12.36
Null hypothesis (H0): There is no statistically significant difference in the mean values of
Overrun and other independent variables House and WT.
Alternative hypothesis (H1): There is a statistically significant difference in the mean values of
Overrun and other independent variables House and WT.
A. Identification of varaious factors and treatments
There have been use of factors for the treatments such as Overrun (24), House (24) and
WT (24).
B. Conducting research through ANOVA table
Regression
Descriptive Statistics
Mean Std. Deviation N
OVERRUN 510.54 20.504 24
HOUSE 2.50 1.142 24
WT 1.50 .511 24

Correlations
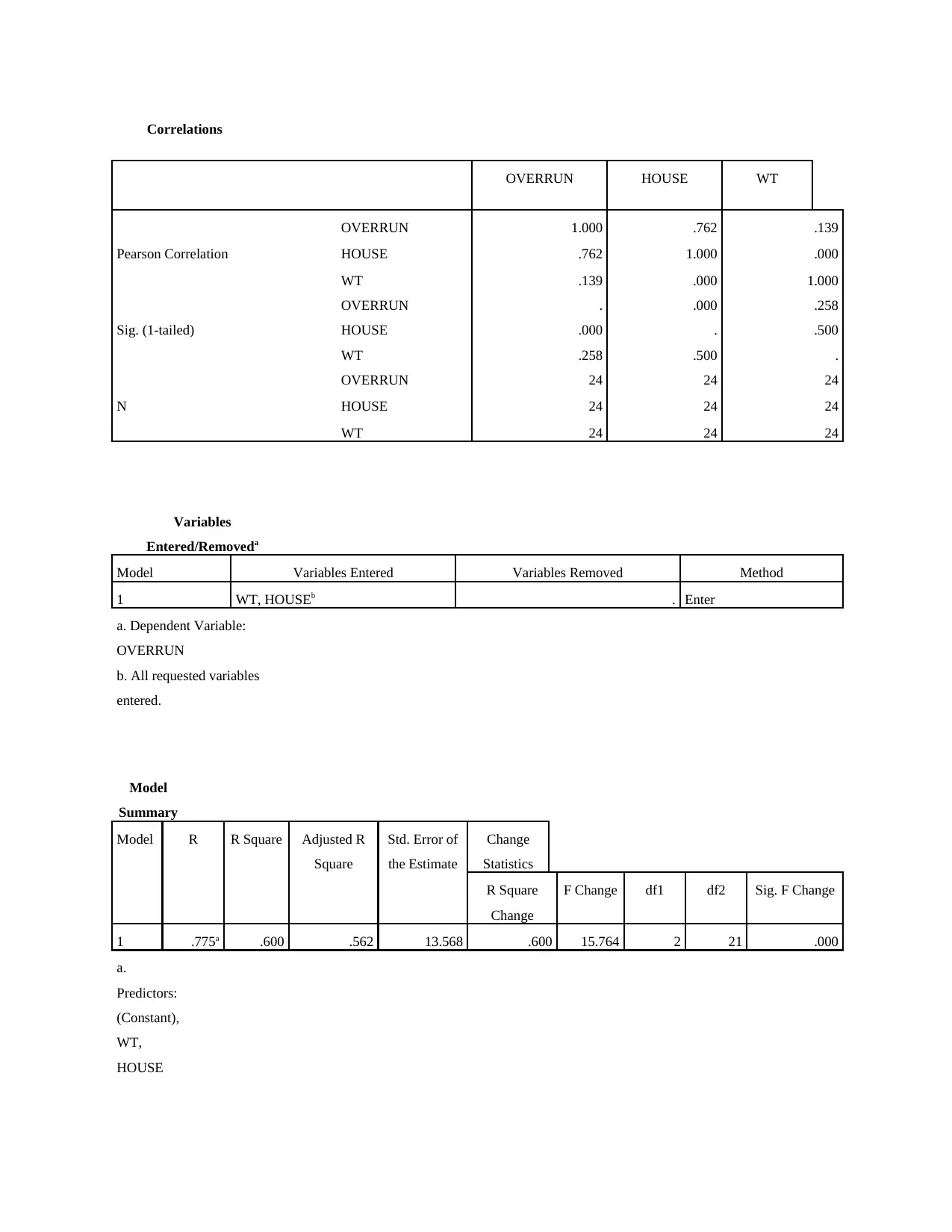
OVERRUN HOUSE WT
Pearson Correlation
OVERRUN 1.000 .762 .139
HOUSE .762 1.000 .000
WT .139 .000 1.000
Sig. (1-tailed)
OVERRUN . .000 .258
HOUSE .000 . .500
WT .258 .500 .
N
OVERRUN 24 24 24
HOUSE 24 24 24
WT 24 24 24
Variables
Entered/Removeda
Model Variables Entered Variables Removed Method
1 WT, HOUSEb . Enter
a. Dependent Variable:
OVERRUN
b. All requested variables
entered.
Model
Summary
Model R R Square Adjusted R
Square
Std. Error of
the Estimate
Change
Statistics
R Square
Change
F Change df1 df2 Sig. F Change
1 .775a .600 .562 13.568 .600 15.764 2 21 .000
a.
Predictors:
(Constant),
WT,
HOUSE

ANOVAa
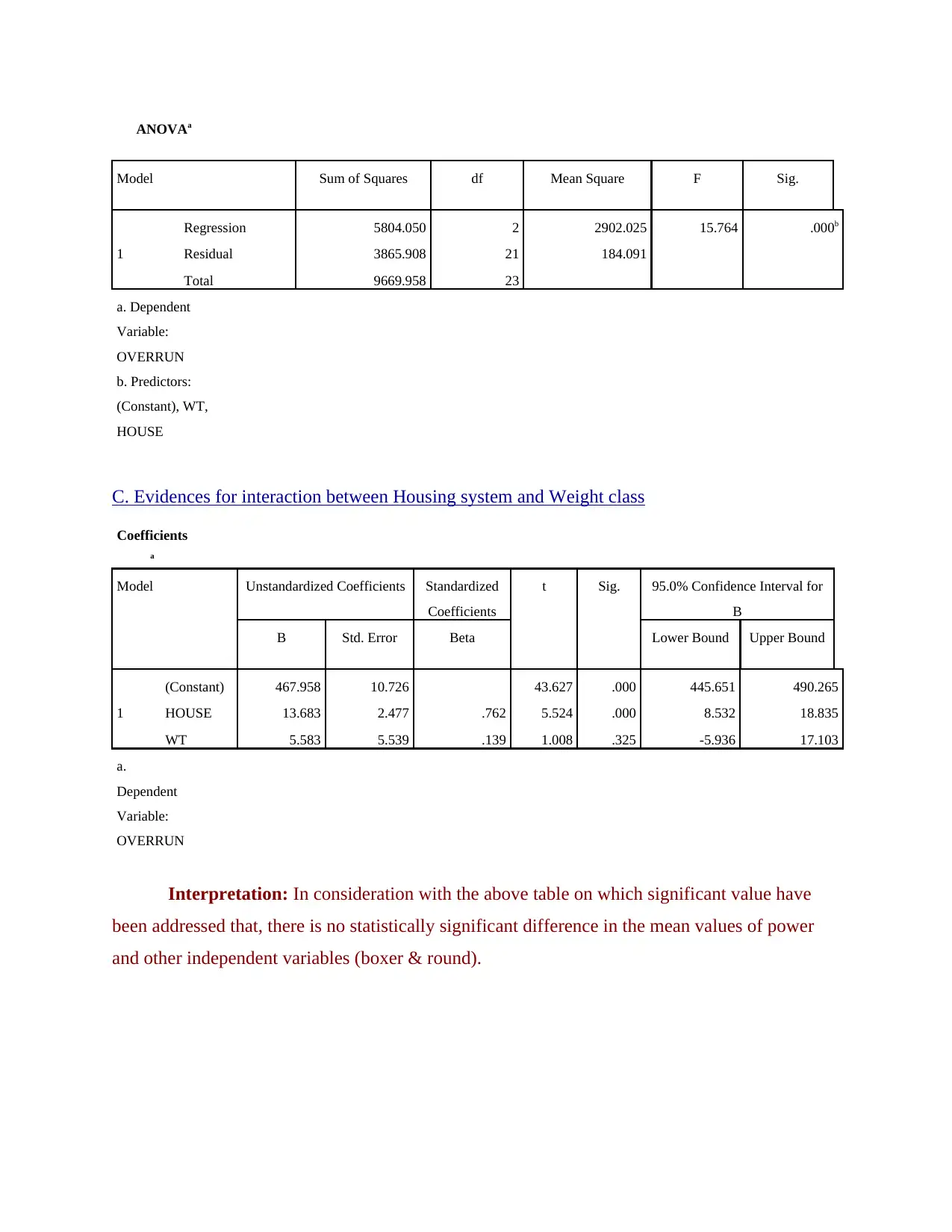
Model Sum of Squares df Mean Square F Sig.
1
Regression 5804.050 2 2902.025 15.764 .000b
Residual 3865.908 21 184.091
Total 9669.958 23
a. Dependent
Variable:
OVERRUN
b. Predictors:
(Constant), WT,
HOUSE
C. Evidences for interaction between Housing system and Weight class
Coefficients
a
Model Unstandardized Coefficients Standardized
Coefficients
t Sig. 95.0% Confidence Interval for
B
B Std. Error Beta Lower Bound Upper Bound
1
(Constant) 467.958 10.726 43.627 .000 445.651 490.265
HOUSE 13.683 2.477 .762 5.524 .000 8.532 18.835
WT 5.583 5.539 .139 1.008 .325 -5.936 17.103
a.
Dependent
Variable:
OVERRUN
Interpretation: In consideration with the above table on which significant value have
been addressed that, there is no statistically significant difference in the mean values of power
and other independent variables (boxer & round).

REFERENCES
Books and Journals
Jha, P. K. and et.al., 2018. Evaluating the applicability of using daily forecasts from seasonal
prediction systems (SPSs) for agriculture: a case study of Nepal’s Terai with the NCEP
CFSv2. Theoretical and Applied Climatology, pp.1-14.
Kimani, J. G., 2018. PRACTICAL STATISTICAL PACKAGE FOR SOCIAL SCIENCES
(SPSS) TRAINING AND RESEARCH COMPETENCE AMONG STUDENTS AT THE
UNIVERSITY OF NAIROBI (LOWER KABETE CAMPUS). Journal of Statistics and
Actuarial Research. 1(1). pp.23-38.
Kimani, J. G., Waititu, A. and Iravo, M., 2017. Linking Practical Spss Training to Research
Competence Among Postgraduate Students at Jomo Kenyatta University of Agriculture
and Technology (JKUAT), Westland’s Campus. American Journal of Education and
Practice. 2(1). pp.43-56.
Online
Annotated output. 2018. [Online]. Available through :<
https://stats.idre.ucla.edu/other/annotatedoutput/>.