Confidence Interval Calculations for Sales and Proportion Data

The assignment provides detailed calculations for confidence interval analysis of sales price and proportion of brick veneer data. It includes point estimates, standard errors, and z-scores for both sample and population mean, as well as sample and population proportions. The results are presented in a tabular format, with calculated values and explanations provided for each step. The assignment also discusses the implications of using different confidence levels (99% vs 95%) on the precision of the results.

BUSINESS STATISTICS

TABLE OF CONTENTS
INTRODUCTION...........................................................................................................................1
TASK 2............................................................................................................................................1
(a)Properties in sample consist of brick building........................................................................1
(b)Building type occur more frequently in sample size...............................................................1
© Proportion of weatherboard buildings.....................................................................................1
TASK 3............................................................................................................................................1
(a)Sorted data of sales priece.......................................................................................................1
(b)Percentile calculation..............................................................................................................3
© Things indicated by 70th percentile..........................................................................................3
(d)IQR..........................................................................................................................................3
TASK 4............................................................................................................................................4
(a)Descriptive statistics tables for sales price sample..................................................................4
(b).................................................................................................................................................4
© Appropriate measure of central tendency................................................................................4
TASK 5............................................................................................................................................5
(a)Normal distribution of data.....................................................................................................5
(b)Sold price observations by standard normal table..................................................................5
© Computation of observation....................................................................................................6
TASK 6............................................................................................................................................6
(a)Descriptive statistics................................................................................................................6
(b)Evaluation of reliability of confidence interval values...........................................................7
TASK 7............................................................................................................................................7
(a).................................................................................................................................................7
(b)Proportion at 95% confidence interval....................................................................................8

© Comparison of results..............................................................................................................9
REFERENCES..............................................................................................................................10
Table 1Calculation of percentile......................................................................................................3
Table 225th and 75th Percentile......................................................................................................3
Table 3Calculation of inter quartile range.......................................................................................3
Table 4Descriptive statistics table...................................................................................................4
Table 5Computation of observation................................................................................................6
Table 6Computation of mean value.................................................................................................6

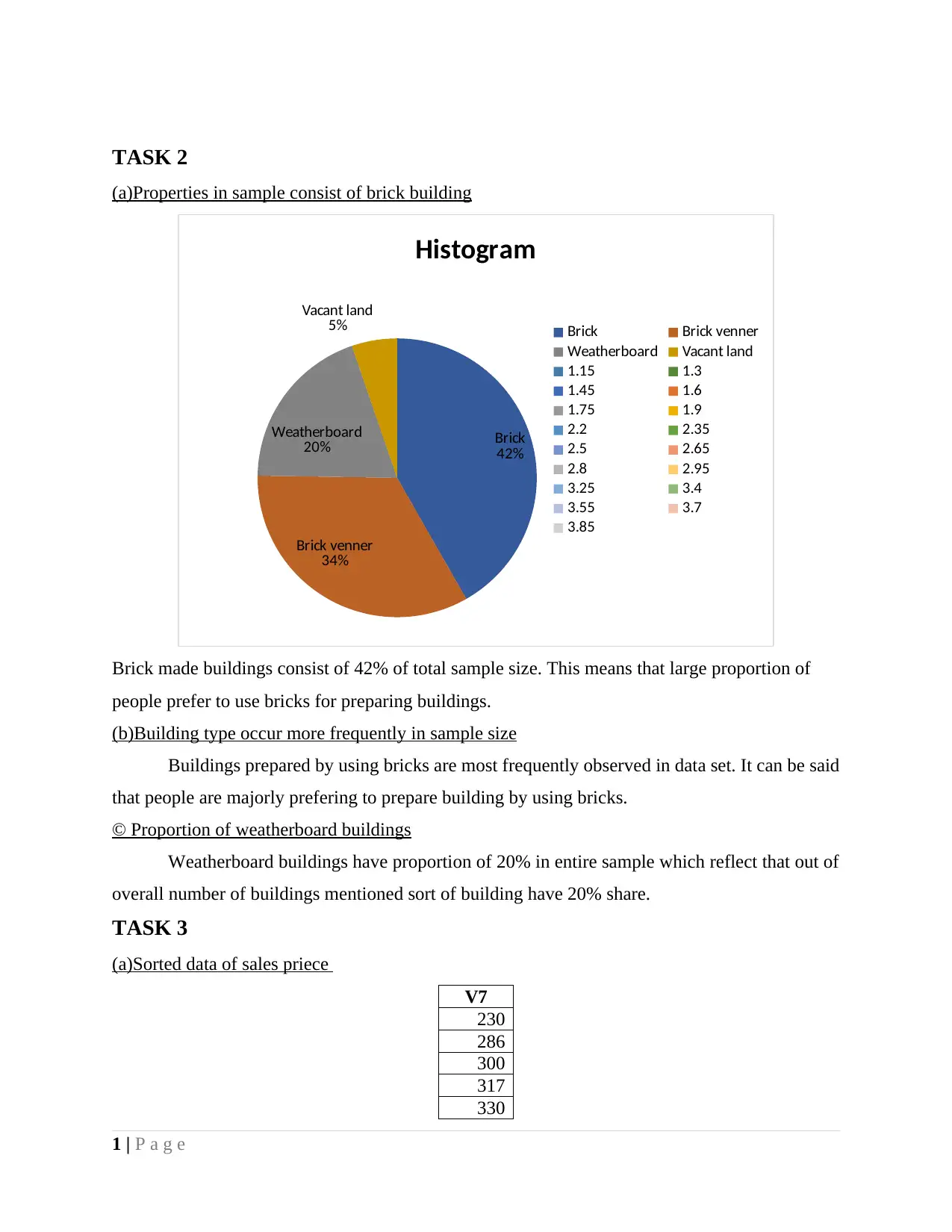
TASK 2
(a)Properties in sample consist of brick building
Brick
42%
Brick venner
34%
Weatherboard
20%
Vacant land
5%
Histogram
Brick Brick venner
Weatherboard Vacant land
1.15 1.3
1.45 1.6
1.75 1.9
2.2 2.35
2.5 2.65
2.8 2.95
3.25 3.4
3.55 3.7
3.85
Brick made buildings consist of 42% of total sample size. This means that large proportion of
people prefer to use bricks for preparing buildings.
(b)Building type occur more frequently in sample size
Buildings prepared by using bricks are most frequently observed in data set. It can be said
that people are majorly prefering to prepare building by using bricks.
© Proportion of weatherboard buildings
Weatherboard buildings have proportion of 20% in entire sample which reflect that out of
overall number of buildings mentioned sort of building have 20% share.
TASK 3
(a)Sorted data of sales priece
V7
230
286
300
317
330
1 | P a g e

350
350
353
353
370.5
382
409
410
410
410
410.5
415
432.5
441
441.5
445
450
455
455
467
479.5
490
516
581
615
620
627.5
631
648
741
831
880
882.5
890
900
1215
1360
1360
1424
1606
2020
2050
2 | P a g e

(b)Percentile calculation
(1)70th percentile
Table 1Calculation of percentile
Lp
n 50
P/100 0.7
70th Percentile 35
(2)First and third quartile
Table 225th and 75th Percentile
n 50
P/100 0.25
25th Percentile 12.5
n 50
P/100 0.75
75th Percentile 37.5
© Things indicated by 70th percentile
70th percentile indicate 70% portion of sample. Thus, 70% portion of data can be
identified by using percentile method.
(d)IQR
Table 3Calculation of inter quartile range
n 50
P/100 0.25
25th Percentile 12.5
n 50
P/100 0.75
75th Percentile 37.5
IQR 25
IQR reflect gap that exist between first and third quartile (Coladarci and et.al., 2010). There is
sufficient gap between values of both percentiles which means that there are number of
observations between both values.
3 | P a g e

TASK 4
(a)Descriptive statistics tables for sales price sample
Table 4Descriptive statistics table
V7
Mean 660.4362
Standard Error 63.94825
Median 455
Mode 410
Standard Deviation 438.4071
Sample Variance 192200.8
Kurtosis 2.867371
Skewness 1.829762
Range 1820
Minimum 230
Maximum 2050
Sum 31040.5
Count 47
Confidence
Level(99.0%) 171.8298
(b)
IFUL= Q3 + 1.5 x IQR
=35+1.5*25
=72.5
IFLL = Q1 – 1.5 x IQR
=12.5+1.5*25
=50
© Appropriate measure of central tendency
(1)
Mean as measure of central tendency used because it reflect average value of variable
sold price data. It can be said that mean value is 660.43 and this means that on an average
building are sold at value of 660.
(2)
4 | P a g e

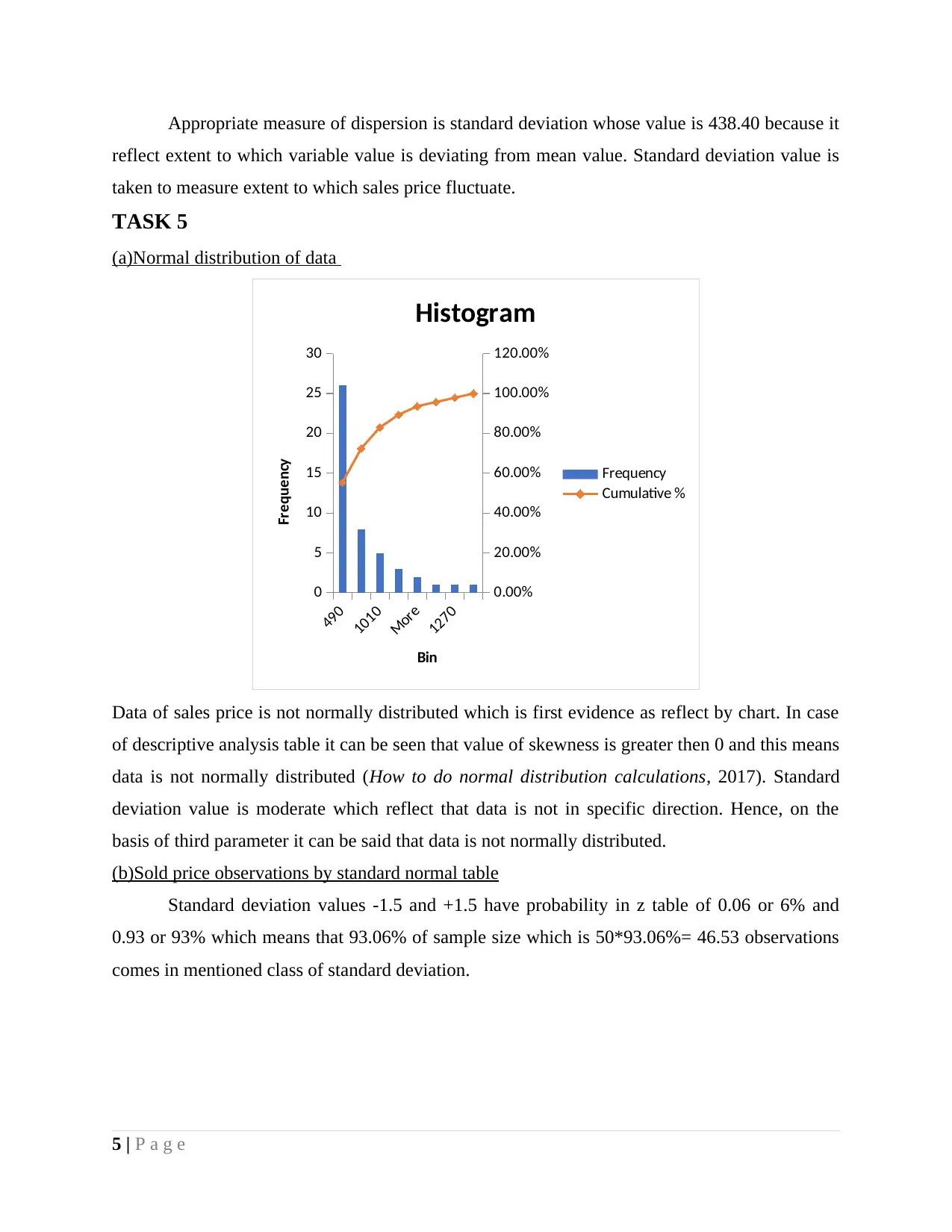
Appropriate measure of dispersion is standard deviation whose value is 438.40 because it
reflect extent to which variable value is deviating from mean value. Standard deviation value is
taken to measure extent to which sales price fluctuate.
TASK 5
(a)Normal distribution of data
490
1010
More
1270
0
5
10
15
20
25
30
0.00%
20.00%
40.00%
60.00%
80.00%
100.00%
120.00%
Histogram
Frequency
Cumulative %
Bin
Frequency
Data of sales price is not normally distributed which is first evidence as reflect by chart. In case
of descriptive analysis table it can be seen that value of skewness is greater then 0 and this means
data is not normally distributed (How to do normal distribution calculations, 2017). Standard
deviation value is moderate which reflect that data is not in specific direction. Hence, on the
basis of third parameter it can be said that data is not normally distributed.
(b)Sold price observations by standard normal table
Standard deviation values -1.5 and +1.5 have probability in z table of 0.06 or 6% and
0.93 or 93% which means that 93.06% of sample size which is 50*93.06%= 46.53 observations
comes in mentioned class of standard deviation.
5 | P a g e

© Computation of observation
Table 5Computation of observation
Mean 624.6926486
STDEV 1.5
Minimum
range -1.5
Maximum
range 1.5
Lower bound 622.4426486
Upper bound 626.9426486
Answer
2
observations
Mean+STDEV*minimum range
=624.69+1.5*-1.5
=622
Mean+STDEV*maximum range
=624.69+1.5*1.5
=626.94
TASK 6
(a)Descriptive statistics
(1)
Table 6Computation of mean value
V7
Mean 660.4362
Standard Error 63.94825
Median 455
Mode 410
Standard Deviation 438.4071
Sample Variance 192200.8
Kurtosis 2.867371
Skewness 1.829762
Range 1820
Minimum 230
Maximum 2050
Sum 31040.5
Count 47
Confidence
Level(90.0%) 107.3474
6 | P a g e

Point estimate of mean is 660 for populaiton mean.
(2)90% confidence interval value
Value of variable sales price at 90% confidence interval is 107.34.
(3)Explaination of confidence interval
Confidence interval reflect likely value of variable in case individual is confident by
certain percentage like 90% that mean value will remain in existance in upcoming time period.
Mean= 660.44
STDEV=438.41
Square root of sample= 7.07
STDEV/SR=438.41/7.07=62
Z*STDEV/SR= 1.64*62=101.68
Mean-(Z*STDEV/SR)= 660.44-101.68= 558.76
Mean-(Z*STDEV/SR)= 660.44+101.68= 762.12
Means that if analyst is confident by 90% that in future mean sales price will be 660.44 then
sales price may be in range of 558 to 762.
(b)Evaluation of reliability of confidence interval values
There is difference between population and sample mean. Population mean is 650 and
sample mean is 660 as it can be observed that there is difference of only 10 between both. Hence,
this will not have much impact on reliability of results. So, obtained confidence interval is
satisfactory.
TASK 7
(a)
(1) Point estimate of brick veneer
Transformed V4
Mean 0.38
Standard Error 0.069340921
Median 0
Mode 0
Standard Deviation 0.490314351
Sample Variance 0.240408163
7 | P a g e

Kurtosis
-
1.814290359
Skewness 0.509876978
Range 1
Minimum 0
Maximum 1
Sum 19
Count 50
Confidence Level
(99.0%) 0.185830337
Mean= 0.38
STDEV= 0.349
Square root of sample= 7.07
STDEV/SR=0.349/7.07=0.06
Z*STDEV/SR= 2.58*0.06=0.17
Mean-(Z*STDEV/SR)= 0.38-0.17= 0.20
Mean-(Z*STDEV/SR)= 0.38+0.17= 0.56
Point estimate proportion of brick venneer is 19 in overall sample size in respect to population.
At 99% confidence interval proportion is 0.20% to 0.56% that is expect to capture population
mean.
(b)Proportion at 95% confidence interval
Sample
proportion 0.38
n 50
1-sample
proportion 0.62
sample
proportion*1-SP 0.38*0.62=0.23
Count
0.2356/50=0.0047
12
Sample error
√0.0047142=0.06
8644009
Population
proportion 0.4175
n 400
1-Population
proportion 1-0.41=0.62
Population 0.4175*0.62=0.25
8 | P a g e

proportion*1-PP 885
Count
0.25585/400=
0.000647125
Population error
√0.000647125=
0.025438652
0.5/n 0.5/400= 0.00125
0.026688652
Sample
proportion 0.38
Z.95 0.026688652
Sample error 0.068644009
Lower limit
0.38-
(0.0266*0.068)-
0.001=
0.377167984
Upper limit
0.38-
(0.0266*0.068)+0.
001=
0.379167984
Results reflect that 37% data is in respect to brick venner in sample size. Empirical rule in case
of porporition is that 68% of sample size lie in one standard deviation and 95% of same lies in
range of second standard deviation.
© Comparison of results
Change in precision is expected because in case of former confidence interval of 99% is
taken in to account but in case of other one confidence interval of 95% is considered. Hence,
different results are obtained.
9 | P a g e

REFERENCES
Books and Journals
Coladarci, T. and et.al., 2010. Fundamentals of statistical reasoning in education. John Wiley &
Sons.
Online
How to do normal distribution calculations, 2017. [Online]. Available through:<
https://statistics.laerd.com/statistical-guides/normal-distribution-calculations.php>.
[Accessed on 26th September 2017].
10 | P a g e