Discrete Mathematics Assignment 4: Relations, Graphs, and Matrices

This assignment solution delves into key concepts of discrete mathematics, including relations, graphs, and matrices. It begins by analyzing relations, specifically examining equivalence relations, and determining properties like reflexivity, symmetry, and transitivity. The solution then constructs ...Read More

Assignment 4, Trimester 3, 2017
Discrete mathematics
Assignment 4
Institution Name
Student Name

Assignment 4, Trimester 3, 2017
1. Relations R on a set A={1,2,3,4 }
Find the matrix representing R and the directed graph corresponding to R
i. R= { ( 1,3 ) , ( 2,3 ) , ( 3,1 ) , ( 3,2 ) , ( 4,2 ) , ( 4,4 ) }
R=[
0 0 1 0
0 0 1 0
1 1 0 0
0 1 0 1
]
The directed graph will be
ii. R={( a , b ) :a2+b2 >8
( 1,1 ) , (1,2 ) , ( 1,3 ) , (1,4 ) , (2,1 ) , ( 2,2 ) ( 2,3 ) , ( 2,4 ) , ( 3,1 ) , ( 3,2 ) , ( 3,3 ) , ( 3,4 ) , ( 4,1 ) , ( 4,2 ) , ( 4,3 ) ,( 4,4)
¿ { ( 1,3 ) , ( 1,4 ) , ( 2,3 ) , ( 2,4 ) , ( 3,1 ) , ( 3,2 ) , ( 3,3 ) , ( 3,4 ) , ( 4,1 ) , ( 4,2 ) , ( 4,3 ) ,(4,4)}
R=[
0 0 1 1
0 0 1 1
1 1 1 1
1 1 1 1
]
Then the graph is
iii. R={( a , b ) :a−b=0 which means a=b }
this gives ( 1,1 ) , ( 2,2 ) , (3,3 ) , (4,4)
¿ here we obtainthe ¿
1 3
2 4
1
4
2
3

Assignment 4, Trimester 3, 2017
R=[
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
]
then the graph will be given by
2. Relations r on the set of non-negative integers
Equivalence relations are reflexive, symmetric and transitive
i. R={( a , b ) :a−bis divisible by 4
To be reflexive the set (a , a)∈ R for all the elements in a
a−a=0, which is divisible by 4
Testing symmetric
If (a , b) ϵR then (b , a) ϵR
For a set ( 20,4 ) there isanother set (4,20) present in R .
If a−b=cwhich is divisible by 4 then b−a=−c which also is divisible by 4. R is
therefore symmetric.
Transitive
A relation R is transitive if whenever ( a , b ) ϵR , ( b , c ) ϵR then(a , c)ϵR
Assuming the numbers ( 27,30 ) as ( a , b )
27−3= 24
4 =6 hence divisible by 4
then ( b , c ) =(3,27), 3−27=−24
4 =−6 hence divisible by 4
for this case there must be a number
( a , c )=;27−27= 0
4 =0 which also is divisible by 4
the relation R is thus transitive
in conclusion R satisfies all the properties of an equivalence relation.
ii. r ={( a , b ) ;a+ 3 bid divisible by 4
Reflexive
1 2
4 3

Assignment 4, Trimester 3, 2017
( a , a ) ϵRfor every element ∈A
a+ 3 a= 4 a
4 =a whichis divisible by 4
The relation therefore satisfies the reflexive property.
Symmetric
If ( a , b ) ∈ Rthen (b , a)∈ R
Now if a+3 b
We use an example of (1,1)
To give ( a+3 b ) −4∧ ( b+3 a ) =4
This shows that all the elements are within the relation hence R is symmetric.
Transitive
If ( a , b )∧ ( b , c ) are presentin R, then (a , c )ϵR
Using an example of ( 2,2 )
¿by 4hence transitive
R thereforesatisfies all the properties of an equivalent relation.
3.
i. R={( a , b ) :a ≡ b(mod 6)
iff n/(a−b)
6
a−b should be an integer
R {( 1,1 ) , ( 1,2 ) , ( 1,3 ) , ( 1,4 ) , ( 1,7 ) , ( 2,1 ) , ( 2,2 ) , ( 2,3 ) , ( 2,4 ) , ( 2,5 ) , ( 2,8 ) , ( 3,1 ) , ( 3,2 ) , ( 3,3 ) , ( 3,4 ) , ( 3,5 ) , ( 3
The equivalent class will be
[ a ]= ( a , b ) : { 6
a−b }whichis an integer
This classes are
[ 0 ]= { 0,6,12,18… } , [ 1 ] = {1,7,13,19 … } , [2 ]= { 2,8,14 … } , [ 3 ] = { 3,9,15 ,21 … } , [ 4 ] = { 4.10,16,22 … } , [ 5
ii.
R={( 1,1 ) , ( 1,3 ) , ( 1,5 ) , ( 3,3 ) , ( 3,1 ) , ( 3,5 ) , ( 5,1 ) , ( 5,3 ) , ( 5,5 ) , ( 2,2 ) , (2,6 ) , ( 6,2 ) , ( 6,6 ) ,(4,4)}
A={1,2,3,4,5,6 }
The equivalent classes are therefore.
[ 1 ] = { 1,3,5 } =[5]
[ 3 ]= {3,1,5 }=[5]
[ 2 ]= { 2,6,6 }=[6]

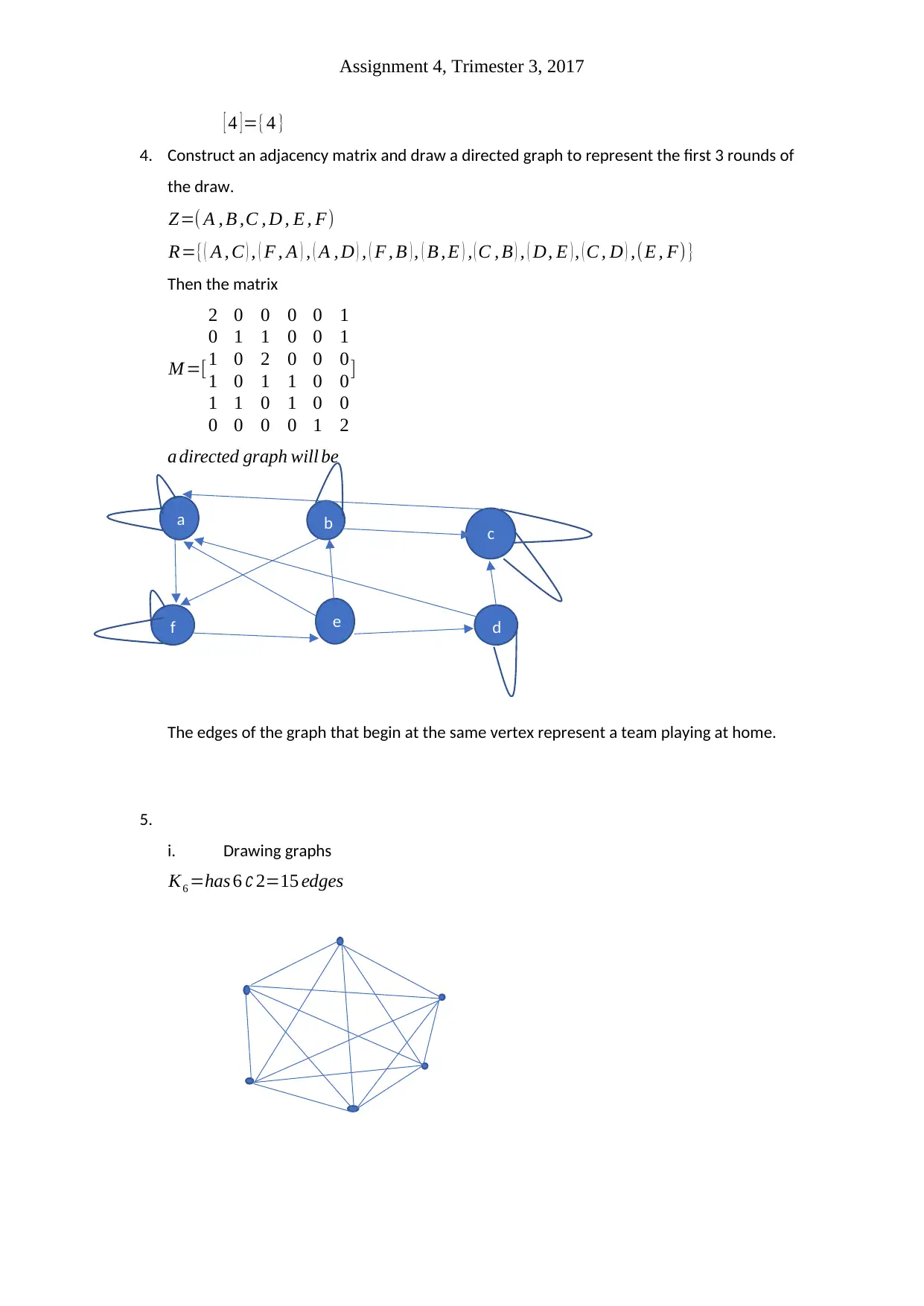
Assignment 4, Trimester 3, 2017
[ 4 ] ={4 }
4. Construct an adjacency matrix and draw a directed graph to represent the first 3 rounds of
the draw.
Z=( A , B ,C , D , E , F)
R={ ( A , C ) , ( F , A ) , ( A , D ) , ( F , B ) , ( B , E ) , ( C , B ) , ( D, E ) , ( C , D ) ,(E , F) }
Then the matrix
M =[
2 0 0 0 0 1
0 1 1 0 0 1
1 0 2 0 0 0
1 0 1 1 0 0
1 1 0 1 0 0
0 0 0 0 1 2
]
a directed graph will be
The edges of the graph that begin at the same vertex represent a team playing at home.
5.
i. Drawing graphs
K6 =has 6 ∁ 2=15 edges
a
f
b c
e d

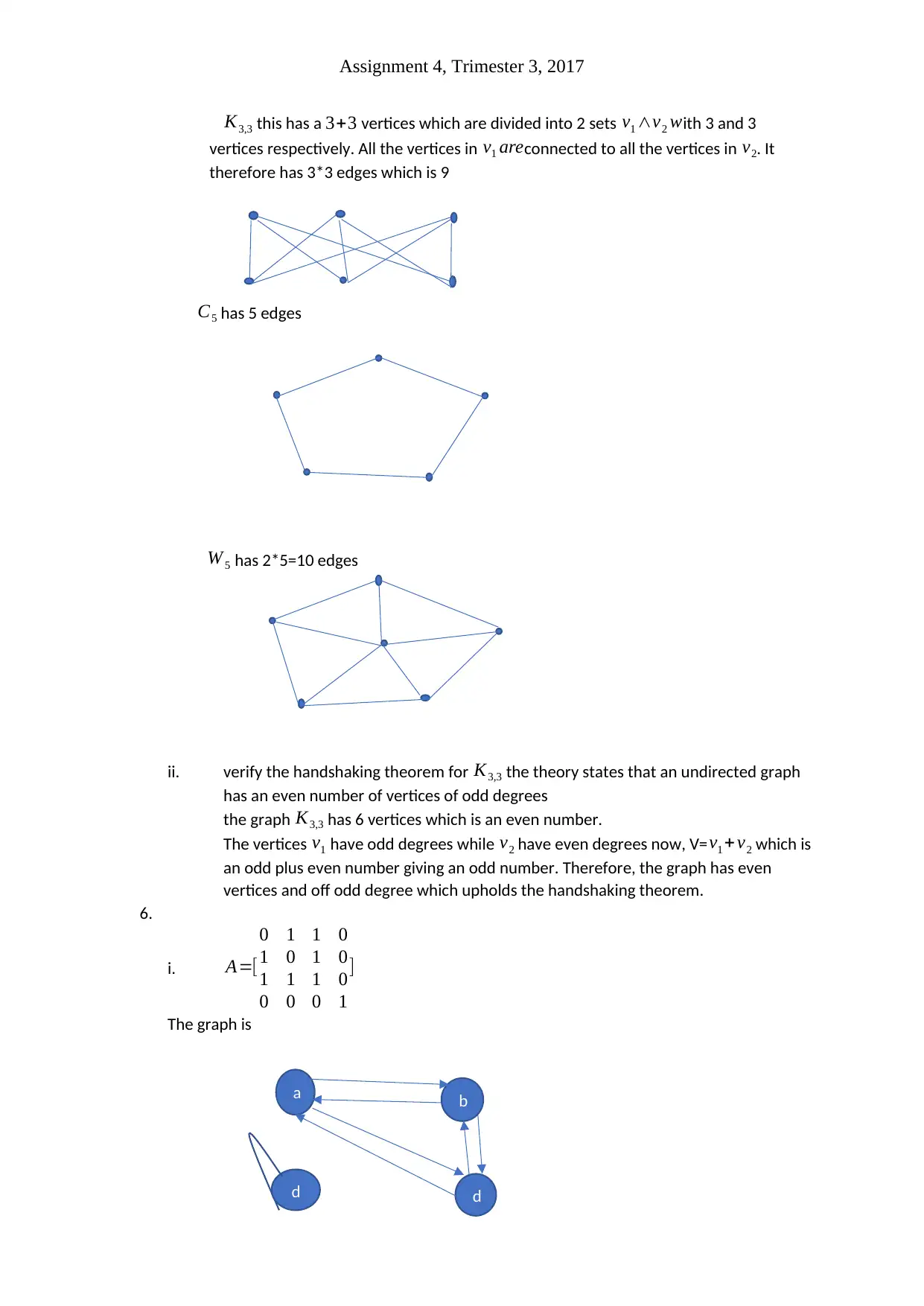
Assignment 4, Trimester 3, 2017
K3,3 this has a 3+3 vertices which are divided into 2 sets v1 ∧v2 with 3 and 3
vertices respectively. All the vertices in v1 areconnected to all the vertices in v2. It
therefore has 3*3 edges which is 9
C5 has 5 edges
W 5 has 2*5=10 edges
ii. verify the handshaking theorem for K3,3 the theory states that an undirected graph
has an even number of vertices of odd degrees
the graph K3,3 has 6 vertices which is an even number.
The vertices v1 have odd degrees while v2 have even degrees now, V=v1 +v2 which is
an odd plus even number giving an odd number. Therefore, the graph has even
vertices and off odd degree which upholds the handshaking theorem.
6.
i. A=[
0 1 1 0
1 0 1 0
1 1 1 0
0 0 0 1
]
The graph is
a
d
b
d

Assignment 4, Trimester 3, 2017
ii. B=[
1 1 3 1
0 0 2 1
2 0 1 1
1 0 3 1
]
7. Paths of length 2 and 3 from vertex to c from the graph of B
A path of length n from u to v is a sequence of n edges beginning at u and ending at v
Length 2
d−a−c
d−d−c
There are 2 paths
Length 3
d−a−d−c
d−d−a−c
There are 2 paths
8.
i. Path from vertex g to c
Simple path does not pass through the same vertex more than once
g−h−d−a−b−f −i−e−c
The path will pass through the vertices
g , h , d , a , b , f , i , e , c
ii. Subgraph of G containing only vertices (e , f , h ,i)
Determining if the matrix is isomorphic to K4 , K2,2 ∨K 1,3
Two graphs are isomorphic when
They have the same number of vertices
Have the same number of edges
Have the same number of vertices of each degree
Now K4 has 6 edges and 4 vertices, the subgraph is not isomorphic to the graph
e f
i h
a
d
b
c

Assignment 4, Trimester 3, 2017
K4 as it has 4 vertices and 5 edges
K2,2 has 4vertices and 4 edges which is not isomorphic to the subgraph.
K1,3 has 4 vertices and 3 edges hence nor isomorphic to the subgraph.
References
Diestel, R. (2005). Graph Theory. Springer.
Frank Harary, R. Z. (1965). Structural Models: An Introduction to the Theory of Directed Graphs. New
York: Wiley.