Assignment on Number System, Permutation & Combination, Differential Equations and Geometry

This assignment consists of four parts, covering topics like number system, permutation & combination, differential equations and geometry. It includes questions and solutions on these topics.

Contents
Introduction...........................................................................................................................................2
LO1........................................................................................................................................................3
Part One: Number Theory.................................................................................................................3
GCD................................................................................................................................................3
LCM..............................................................................................................................................3
Prime Numbers..............................................................................................................................4
Python Code..................................................................................................................................4
To Calculate LCM.........................................................................................................................4
Part Two: Series and Sequences........................................................................................................6
Solution: 2.1...................................................................................................................................6
Solution 2.2....................................................................................................................................6
LO2........................................................................................................................................................8
Part 1.................................................................................................................................................8
Solution 1.1....................................................................................................................................8
Solution 1.2....................................................................................................................................8
LO3......................................................................................................................................................10
Part 1...............................................................................................................................................10
Solution 3.1..................................................................................................................................10
Solution 3.2..................................................................................................................................10
Part Two: Vectors............................................................................................................................11
Solution 3.4..................................................................................................................................11
Solution 3.5..................................................................................................................................11
LO4......................................................................................................................................................13
Part One: Calculus (Differential ).....................................................................................................13
Solution 1.....................................................................................................................................13
Part 2: Calculus (Integral)................................................................................................................14
Solution 4.2.1...............................................................................................................................14
Solution 4.2.2...............................................................................................................................15
Conclusion...........................................................................................................................................17
Reference............................................................................................................................................18

Introduction
This assignment consists of four parts. In the first part of the assignment
brief introduction of GCD, LCM and prime numbers is given. A python code
is written for the above mentioned topics and screenshot of the output is
pasted in the file, this part consist of 2 numerical are given which gives us
the understanding of number system. In the second part there are 2
subparts which explains permutation & combination. In the third part
solution are written with respect to coordinate system. In the last part
differential and integration questions are solved.

LO1
Part One: Number Theory
GCD
GCD stands for “Greatest Common Divisor”. GFC (Greatest Common Factor) is the other
name for GCD. This is performed using at least two numbers which aren’t zero. Highest
integer which divides all other integers is GCD and it should be positive. (GCD, 2019)
For Example:
Number 1: 132
Number 2: 1260
Number 3: 2016
Solution:
Number 1: 12 * 11= 132
Number 2: 12 * 5 * 3 * 7 = 1260
Number 3: 12 * 4 * 6 * 7 = 2016
The GCD for the above numbers is 12 as it is the highest positive number which is also
divisible by all other numbers.
LCM
LCM stands for “Least Common Multiple”. In this smallest common multiple is taken in
consideration. This is calculated between two or more integer. (LCM, 2019)
For Example:
Number 1: 216
Number 2: 420
Number 3: 210
Solution:

Number 1: 2 * 2 * 2 * 3 *3 * 3 = 216
Number 2: 2 * 2 * 3 * 5 * 7 = 420
Number 3: 2 * 3 * 5 * 7 = 210
In this the LCM is 30 as 2, 3 & 5 are common as they can divide the above number.
Prime Numbers
The factors of prime number are 1 and itself. Prime numbers have only 2 factors. For
example numbers 7, 5, 3, 2, 1 as they have only 1 and the number itself as two factors.
Python Code
To make it convenient for calculating LCM and GCD of two integer numbers a program is
created in python written below.
To Calculate LCM
def lcm(q,w):
if q < w:
smaller = w
else:
smaller = q
while(True):
if((smaller % w == 0) and (smaller % q == 0)):
lcm = smaller
break
smaller += 1
return lcm
num_1=int(input(" Enter first number: "))
num_2=int(input(" Enter Second number: "))

print("The L.C.M. of {} and {} is ".format(num_1,num_2),lcm(num_1,num_2))
Output
(python, 2019)
To Calculate GCD
def GCD(q, w):
if q < w:
greater = q
else:
greater = w
for i in range(1, greater+1):
if((a % i == 0) and (b % i == 0)):
gcd = i
return gcd
num_1=int(input("Enter first number"))
num_2=int(input("Enter Second number"))
print("The L.C.M. of {} and {} is ".format(num_1,num_2),GCD(num_1,num_2))
Output:

Part Two: Series and Sequences
Solution: 2.1
Sum of natural numbers which lies between one & one thousand and are divisible by seven
can be calculated by the formula
Sn=n/2 (l+a), where Sn stands for sum of numbers,
n stands for total number,
l stands for last number divisible,
a stands for divisor.
n = 142,
l = 994,
a = 7
Sn = 142/2(994+7)
Sn = 71071
Solution 2.2
The figure below shows the bounce of the ball according to the height in centimetres.
 The figure mentioned below shows the path of the ball bouncing. In this the height of
the bounce of the ball decreases with 25% of the previous bounce so the ball will
come almost to rest after 25th bounce.

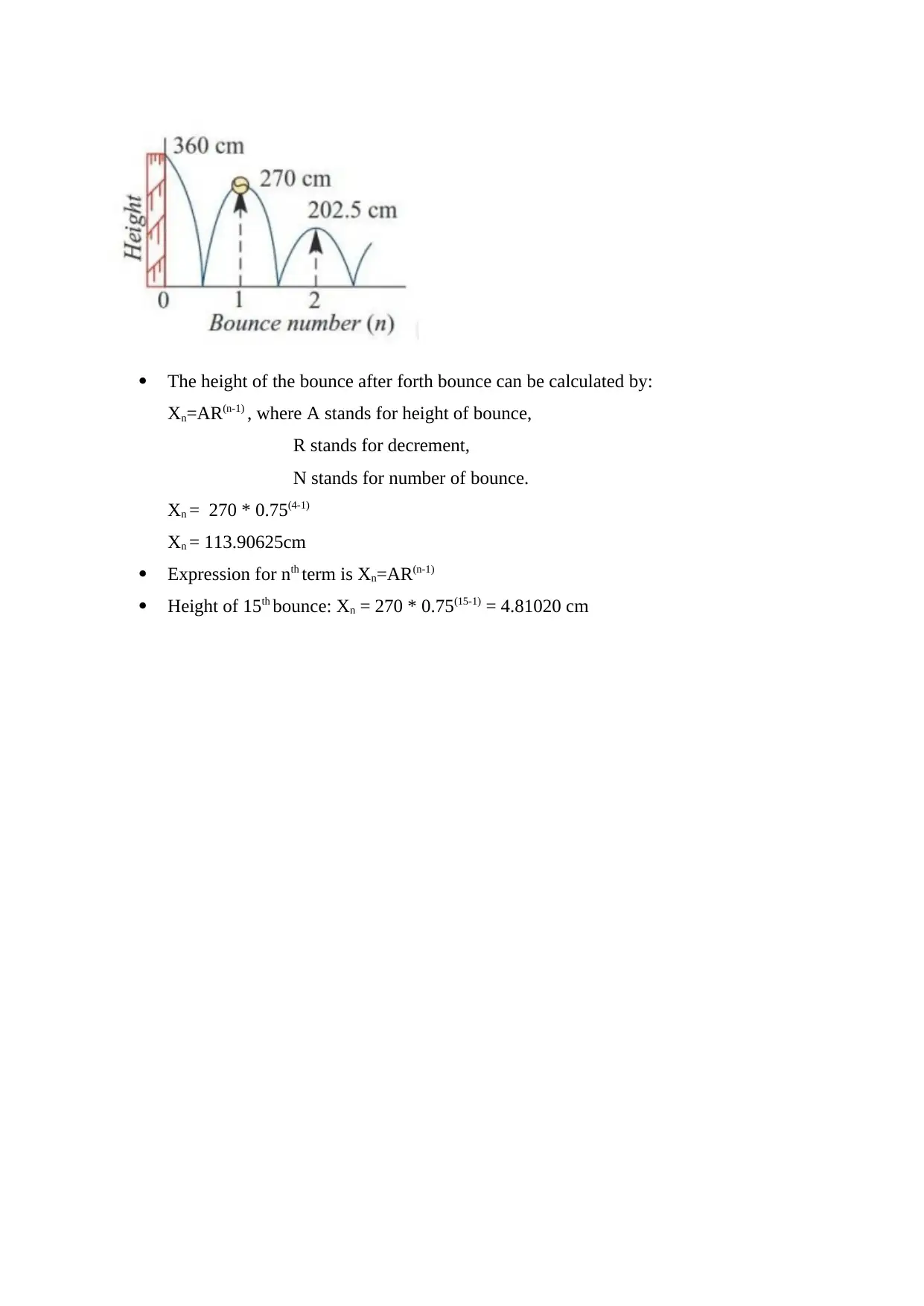
 The height of the bounce after forth bounce can be calculated by:
Xn=AR(n-1) , where A stands for height of bounce,
R stands for decrement,
N stands for number of bounce.
Xn = 270 * 0.75(4-1)
Xn = 113.90625cm
 Expression for nth term is Xn=AR(n-1)
 Height of 15th bounce: Xn = 270 * 0.75(15-1) = 4.81020 cm

LO2
Part 1
Solution 1.1
Man’s probability of selection = 0.25
Women’s probability of selection = 0.33
a. Man and women selected together
0.25 * 0.33 = 0.0825
b. One of them is only selected
0.25 + 0.33 = 0.58
c. Both of them aren’t selected
1 – 0.0825 = 0.9175
Solution 1.2
Total Cards = 52 * 2 = 104
Total heart of Ace = 2
Probability of hearts of ace not drawn: (102 / 2) / (104 / 2) = 0.98
Probability of hearts of ace drawn: 1 – 0.98 = 0.02
Part 2
Solution 2.1
Coin tossed: 5 times
a. Probability (2 heads) = 5C2 / 32
= ((5 * 4 * 3 * 2 * 1) / (2 * 1)(3 * 2 * 1)) / 32
= (120/12) / 32
= 0.3125

b. Probability of 3 heads = 5C3 / 32
= ((5 * 4 * 3 * 2 * 1) / (2 * 1) (2 * 1)) / 32
=(120/4) / 32
= 0.8823

LO3
Part 1
Solution 3.1
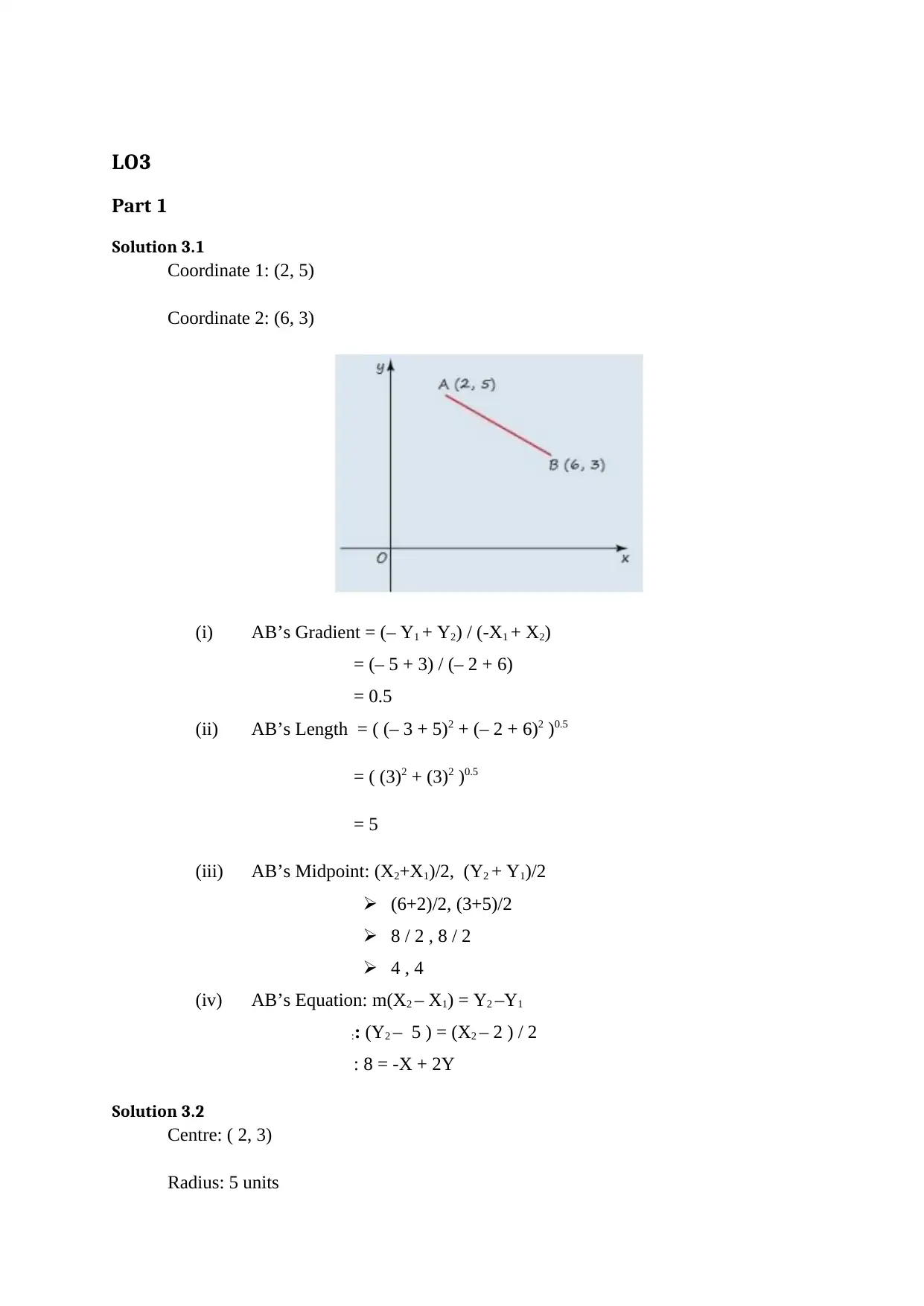
Coordinate 1: (2, 5)
Coordinate 2: (6, 3)
(i) AB’s Gradient = (– Y1 + Y2) / (-X1 + X2)
= (– 5 + 3) / (– 2 + 6)
= 0.5
(ii) AB’s Length = ( (– 3 + 5)2 + (– 2 + 6)2 )0.5
= ( (3)2 + (3)2 )0.5
= 5
(iii) AB’s Midpoint: (X2+X1)/2, (Y2 + Y1)/2
 (6+2)/2, (3+5)/2
 8 / 2 , 8 / 2
 4 , 4
(iv) AB’s Equation: m(X2 – X1) = Y2 –Y1
:: (Y2 – 5 ) = (X2 – 2 ) / 2
: 8 = -X + 2Y
Solution 3.2
Centre: ( 2, 3)
Radius: 5 units

Radius2 = (X – H)2 + (Y – K)2
52 = (X – 2)2 + (Y – 3)2
0 = - 4X - 6Y + X2 - 12 + Y2
Part Two: Vectors
Solution 3.4
North Force is 70 N
East Force is 40 N
Resultant Force= √𝐹𝑦2 + 𝐹𝑥2
Resultant Force = √702 + 402
Resultant Force = √4900 + 1600
Resultant Force = 80.6 N
Magnitude: 𝜃 = tan – 𝑅a/𝑅b
𝜃 = tan – 70/40
𝜃 = 60.2
Solution 3.5
Force 1 = 30N
Force 2 = 40N

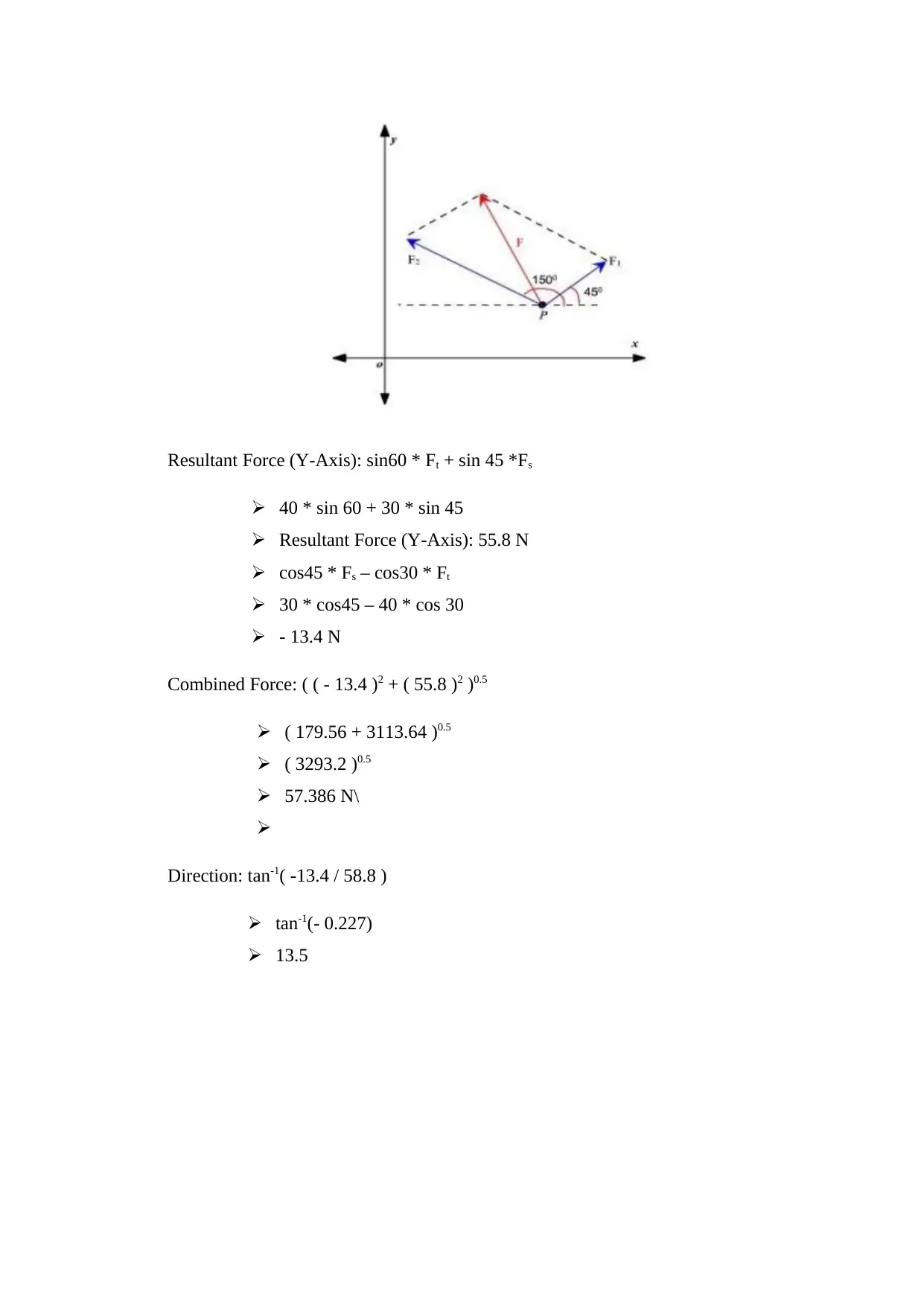
Resultant Force (Y-Axis): sin60 * Ft + sin 45 *Fs
 40 * sin 60 + 30 * sin 45
 Resultant Force (Y-Axis): 55.8 N
 cos45 * Fs – cos30 * Ft
 30 * cos45 – 40 * cos 30
 - 13.4 N
Combined Force: ( ( - 13.4 )2 + ( 55.8 )2 )0.5
 ( 179.56 + 3113.64 )0.5
 ( 3293.2 )0.5
 57.386 N\

Direction: tan-1( -13.4 / 58.8 )
 tan-1(- 0.227)
 13.5

LO4
Part One: Calculus (Differential )
Solution 1
s(t) = 126t2 + 3t4 − 40t3 – 9
Velocity at time t: Vt = d/dx ( 3t4 + 126t2 – 9 − 40t3
Vt = 12 t3 + 252 t – 120 t3
Applying Differential Equation
A (t) = d/dx ( 12 t3 + 252 t – 120 t2 )
A (t) = 36 t2 + 252– 240t
If A (t) = 0
 36 t2 + 252 – 240t = 0
 ( t2 + 21 – 10t)12 t = 0
 ( t – 7) ( t – 3) = 0
 t – 3 = 0; t – 7 = 0
 3, 7 = t
Check if the object is moving right or left
if t = 3, then
 s(t) = 126t2 + 3t4 − 40t3 – 9
 s(3) = 126(3)2 + 3(3)4 – 40(3)3 – 9
 s(3) = 126 * 9 + 3 * 81 – 40 * 27 – 9
 s(3) = 1134 + 243 – 1080 – 9
 s(3) = 288
if t = 7, then
 s(t) = 126t2 + 3t4 − 40t3 – 9
 s(7) = 126(7)2 + 3(7)4 − 40(7)3 – 9
 s(7) = 126 * 49 + 3 * 2401 – 40 * 343 – 9

 s(7) = 6174 + 7203 – 13720 – 9
 s(7) = -352
Part 2: Calculus (Integral)
Solution 4.2.1
g(x) =4 + 2x and f(x) = 1+ x2
Equating the equations
 4 + 2x = 1 + x2
 0 = x2 – 2x – 3
 0 = ( 1 + x )( 3 - x )
 -1, 3 = x
While putting the values of x in the equations
When x = -1
g(x) = 2x + 4
 g(-1) = 2 * (-1) + 4
 g(-1) = 2
f(x) = 1 + x2
 f(-1) = 1 + (-1)2
 f(-1) = 2

When x = 3
2x + 4 = g(x)
 2(3) + 4 = g(x)
 10 = g(x)
1 + x2 = f(x)
 (3)2 + 1 = f(x)
 10 = f(x)
Calculating the area for x = -1
 -1ʃ 3 ( 4 + 2x) dx
 [4x + x2 ]3 – 1
 (32+4*3) - ((-1)2+ 4*(-1))
 21+3
 24
Calculating the area for x = 3
 ʃ 3 (x2 + 1)dx
 [ 3+ (1/3)(3)3 ] – [- (-1)+ (1/3)(-1)3 ]
 12 + (1/3) - 1
 34/3
Area = 24 – 34/3
Area = 12.6 cm2
Solution 4.2.2
V(t) = - 0.4t2 + 2t
Distance (initial hours)= 3
V(t) = ʃ{ 2t - 0.4t3 }ds
By applying limit from 0 to 3

 0ʃ3 {( -0.4t3 ) + 2t } ds = V(t)
 [ 0.1333t3 ]30 + [ t2 ]30 = V(t)
 5.4 km = V(t)

Conclusion
The above assignment has four parts in which topics like number system, permutation &
combination, differential equations and geometry are covered. This assignment consists of
question based on the topics mentioned above.

Reference
LCM (2019). Factoring - Least Common Multiple (LCM) - First Glance. [online] Math.com. Available
at: http://www.math.com/school/subject1/lessons/S1U3L3GL.html [Accessed 6 Mar. 2019].
GCD (2019). Greatest common divisor. [online] En.wikipedia.org. Available at:
https://en.wikipedia.org/wiki/Greatest_common_divisor [Accessed 6 Mar. 2019].
python (2019). Python Program to Find LCM. [online] Programiz.com. Available at:
https://www.programiz.com/python-programming/examples/lcm [Accessed 6 Mar. 2019].
Differential Equations (2019). Differential Equations - Introduction. [online] Mathsisfun.com. Available
at: https://www.mathsisfun.com/calculus/differential-equations.html [Accessed 6 Mar. 2019].