Statistics Assignment - Data Analysis and Statistical Interpretation
VerifiedAdded on 2020/02/24
|14
|1812
|156
Homework Assignment
AI Summary
This statistics assignment analyzes data using various statistical methods. It begins with an overview of simple random sampling and descriptive statistics, including measures of central tendency and dispersion for different variables like alcohol, meals, fuel, and phone expenditures. The assignment then explores frequency distributions, percentages, and interpretations of household spending on utilities, followed by an analysis of percentiles, the 'ownhouse' variable, and family size. Scatter plots are used to examine the relationship between after-tax income and annual expenditure. Finally, the assignment includes a contingency table analysis to determine the probabilities and independence of gender and level of education. The document provides detailed calculations, interpretations, and graphical representations to support the statistical analysis.

Running head: STATISTICS
Statistics
Name of the student:
Name of the university:
Authors note:
Statistics
Name of the student:
Name of the university:
Authors note:
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

1STATISTICS
Table of Contents
Task 1...............................................................................................................................................3
Part 1A.........................................................................................................................................3
Part 1B.........................................................................................................................................3
Part 1C.........................................................................................................................................4
Part 1D.........................................................................................................................................5
Task 2...............................................................................................................................................6
Part 2A.........................................................................................................................................6
Part 2B.........................................................................................................................................6
Part 2C.........................................................................................................................................7
Task 3...............................................................................................................................................8
Part 3A.........................................................................................................................................8
Part 3B.........................................................................................................................................8
Part 3C.........................................................................................................................................9
Part 3D.........................................................................................................................................9
Task 4.............................................................................................................................................10
Part 4A.......................................................................................................................................10
Part 4B.......................................................................................................................................11
Part 4C.......................................................................................................................................11
Table of Contents
Task 1...............................................................................................................................................3
Part 1A.........................................................................................................................................3
Part 1B.........................................................................................................................................3
Part 1C.........................................................................................................................................4
Part 1D.........................................................................................................................................5
Task 2...............................................................................................................................................6
Part 2A.........................................................................................................................................6
Part 2B.........................................................................................................................................6
Part 2C.........................................................................................................................................7
Task 3...............................................................................................................................................8
Part 3A.........................................................................................................................................8
Part 3B.........................................................................................................................................8
Part 3C.........................................................................................................................................9
Part 3D.........................................................................................................................................9
Task 4.............................................................................................................................................10
Part 4A.......................................................................................................................................10
Part 4B.......................................................................................................................................11
Part 4C.......................................................................................................................................11

2STATISTICS
Part 4D.......................................................................................................................................12
Part 4E.......................................................................................................................................12
References......................................................................................................................................13
Part 4D.......................................................................................................................................12
Part 4E.......................................................................................................................................12
References......................................................................................................................................13
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
3STATISTICS
Task 1
Part 1A
Simple Random sampling has been used data in selecting a sample. The sampling is a
representation of the population in a way that every respondent/ individual has an equal
probability to be chosen (Mertens 2014). Also, it is easy to select and is done using random
selection or through random number. It has been used in collection because free from errors, bias
and prejudice, with only minimum knowledge and easily used especially for data analysis using
inferential statistics. Also, the sampling error in this method can be easily calculated.
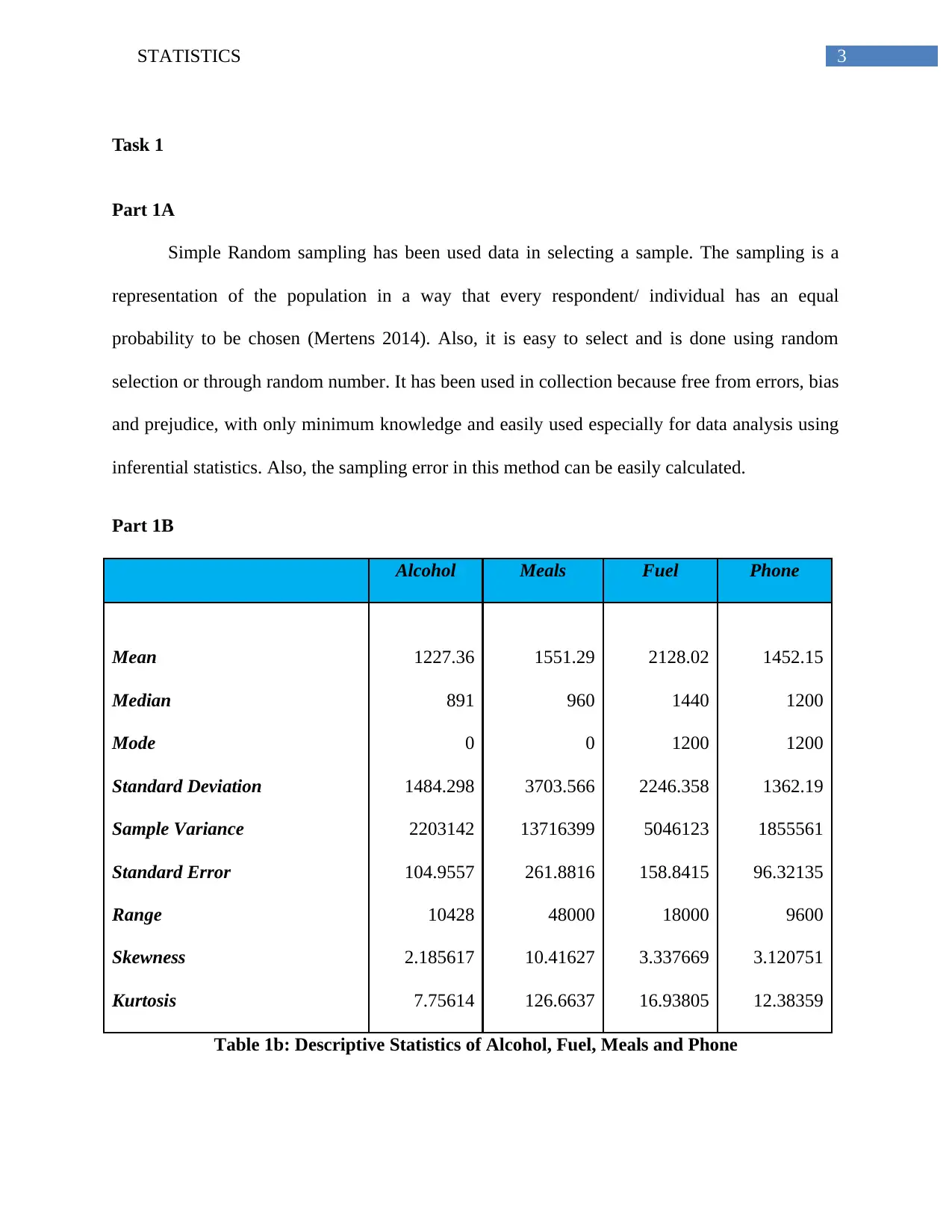
Part 1B
Alcohol Meals Fuel Phone
Mean 1227.36 1551.29 2128.02 1452.15
Median 891 960 1440 1200
Mode 0 0 1200 1200
Standard Deviation 1484.298 3703.566 2246.358 1362.19
Sample Variance 2203142 13716399 5046123 1855561
Standard Error 104.9557 261.8816 158.8415 96.32135
Range 10428 48000 18000 9600
Skewness 2.185617 10.41627 3.337669 3.120751
Kurtosis 7.75614 126.6637 16.93805 12.38359
Table 1b: Descriptive Statistics of Alcohol, Fuel, Meals and Phone
Task 1
Part 1A
Simple Random sampling has been used data in selecting a sample. The sampling is a
representation of the population in a way that every respondent/ individual has an equal
probability to be chosen (Mertens 2014). Also, it is easy to select and is done using random
selection or through random number. It has been used in collection because free from errors, bias
and prejudice, with only minimum knowledge and easily used especially for data analysis using
inferential statistics. Also, the sampling error in this method can be easily calculated.
Part 1B
Alcohol Meals Fuel Phone
Mean 1227.36 1551.29 2128.02 1452.15
Median 891 960 1440 1200
Mode 0 0 1200 1200
Standard Deviation 1484.298 3703.566 2246.358 1362.19
Sample Variance 2203142 13716399 5046123 1855561
Standard Error 104.9557 261.8816 158.8415 96.32135
Range 10428 48000 18000 9600
Skewness 2.185617 10.41627 3.337669 3.120751
Kurtosis 7.75614 126.6637 16.93805 12.38359
Table 1b: Descriptive Statistics of Alcohol, Fuel, Meals and Phone
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
4STATISTICS
Alcohol Meals Fuel Phone
0
500
1000
1500
2000
2500
3000
Box and Whisker Plot of Expenditure on Alcohol,
Meals, Fuel and Phone
Q3-Median
Median - Q1
Q1
Variables
Expenditure
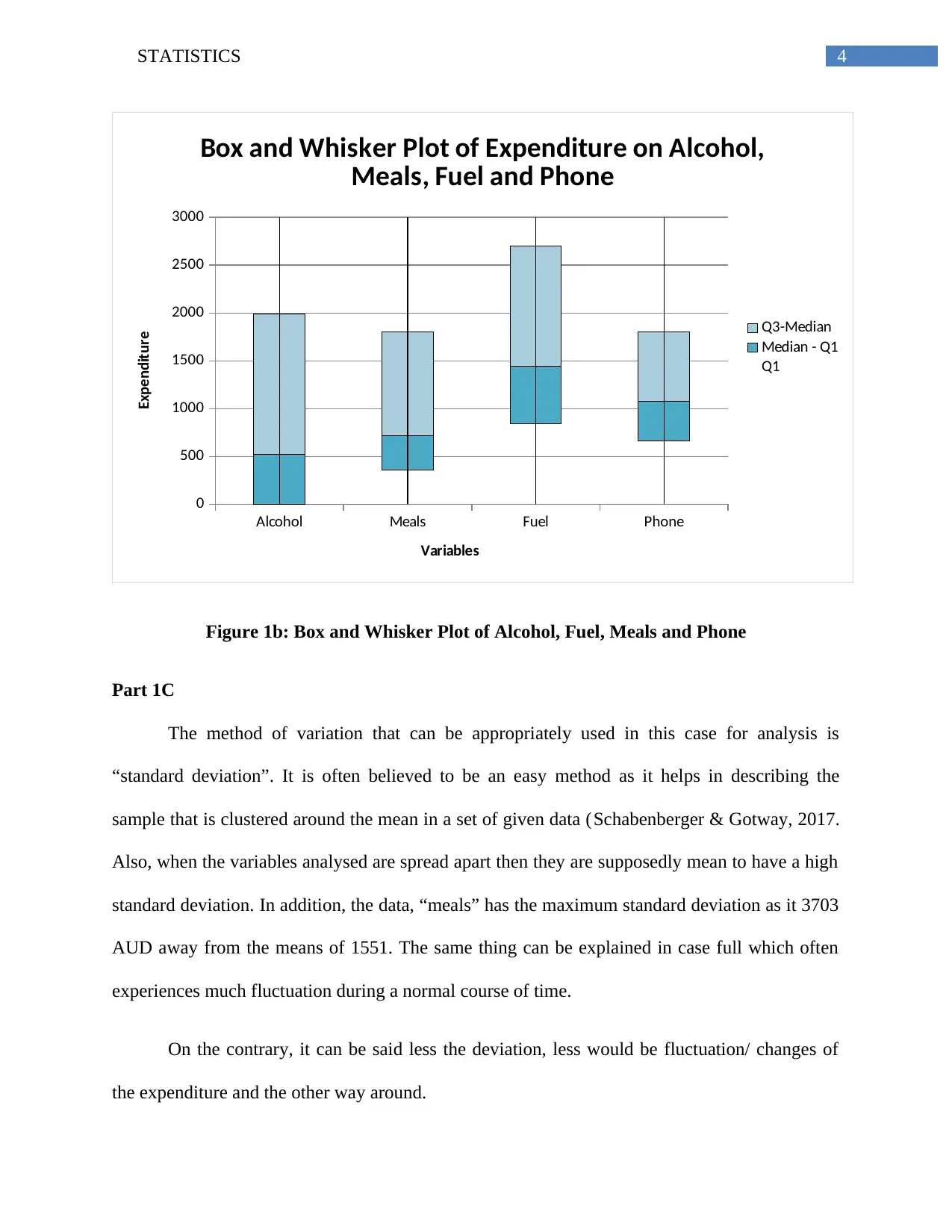
Figure 1b: Box and Whisker Plot of Alcohol, Fuel, Meals and Phone
Part 1C
The method of variation that can be appropriately used in this case for analysis is
“standard deviation”. It is often believed to be an easy method as it helps in describing the
sample that is clustered around the mean in a set of given data (Schabenberger & Gotway, 2017.
Also, when the variables analysed are spread apart then they are supposedly mean to have a high
standard deviation. In addition, the data, “meals” has the maximum standard deviation as it 3703
AUD away from the means of 1551. The same thing can be explained in case full which often
experiences much fluctuation during a normal course of time.
On the contrary, it can be said less the deviation, less would be fluctuation/ changes of
the expenditure and the other way around.
Alcohol Meals Fuel Phone
0
500
1000
1500
2000
2500
3000
Box and Whisker Plot of Expenditure on Alcohol,
Meals, Fuel and Phone
Q3-Median
Median - Q1
Q1
Variables
Expenditure
Figure 1b: Box and Whisker Plot of Alcohol, Fuel, Meals and Phone
Part 1C
The method of variation that can be appropriately used in this case for analysis is
“standard deviation”. It is often believed to be an easy method as it helps in describing the
sample that is clustered around the mean in a set of given data (Schabenberger & Gotway, 2017.
Also, when the variables analysed are spread apart then they are supposedly mean to have a high
standard deviation. In addition, the data, “meals” has the maximum standard deviation as it 3703
AUD away from the means of 1551. The same thing can be explained in case full which often
experiences much fluctuation during a normal course of time.
On the contrary, it can be said less the deviation, less would be fluctuation/ changes of
the expenditure and the other way around.

5STATISTICS
Part 1D
The box plot just like normal distribution is a method of depicting variation using
“method of variation” as quartile. The figure 1b shows fluctuation / changes and the maximum
has been shown by the expenditure on meals, fuels, alcohol and then phone. Moreover, the
annual expenditure distribution of data is higher in upper quartile than in low quartile range
(Hinton, 2014). Comparatively as per the descriptive statistics, meals, fuels, alcohol and phone
have variation as mean> medina > mode depicting positive skewness. However, the maximum
deviation is in meals followed by other like fuels, alcohol and phone.
Part 1D
The box plot just like normal distribution is a method of depicting variation using
“method of variation” as quartile. The figure 1b shows fluctuation / changes and the maximum
has been shown by the expenditure on meals, fuels, alcohol and then phone. Moreover, the
annual expenditure distribution of data is higher in upper quartile than in low quartile range
(Hinton, 2014). Comparatively as per the descriptive statistics, meals, fuels, alcohol and phone
have variation as mean> medina > mode depicting positive skewness. However, the maximum
deviation is in meals followed by other like fuels, alcohol and phone.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
6STATISTICS
Task 2
Part 2A
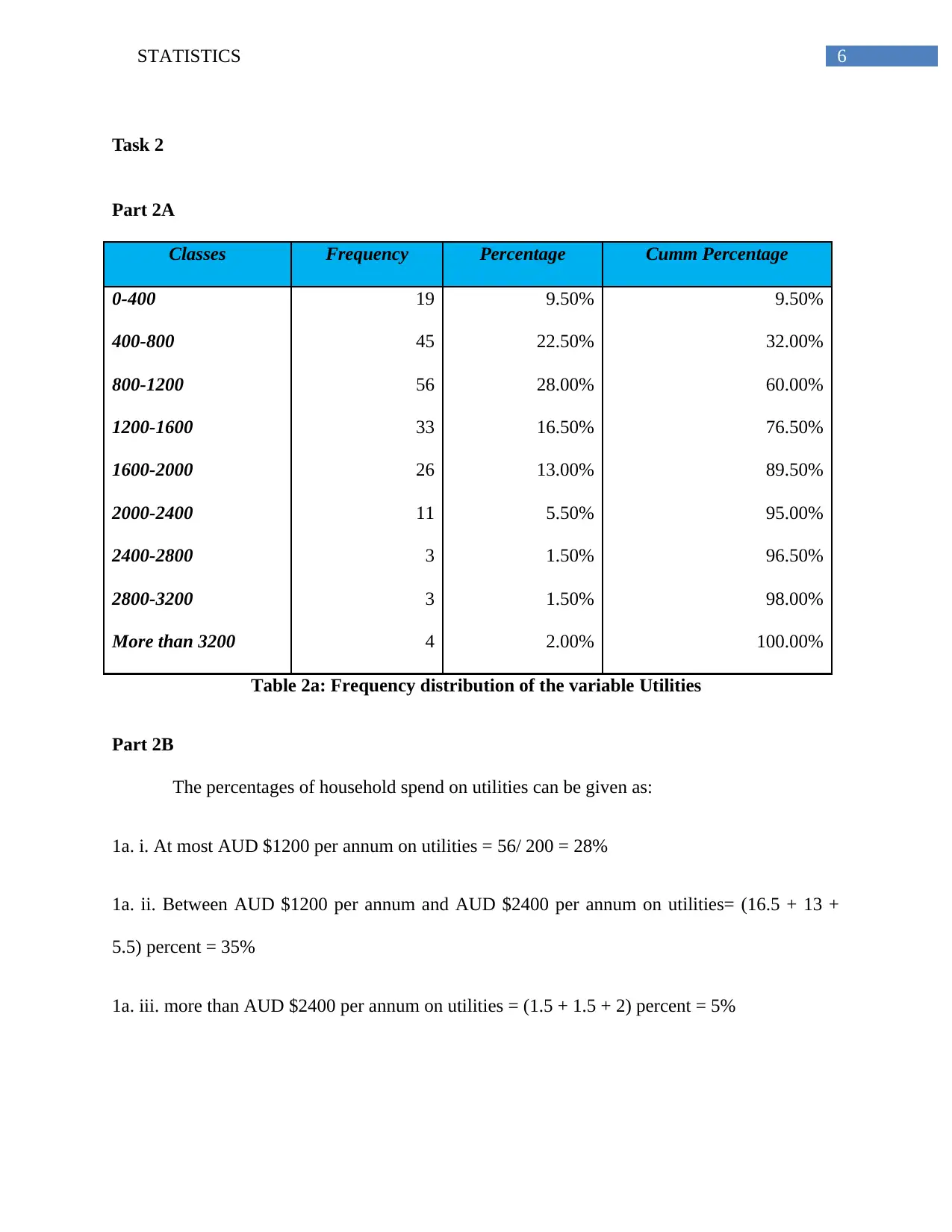
Classes Frequency Percentage Cumm Percentage
0-400 19 9.50% 9.50%
400-800 45 22.50% 32.00%
800-1200 56 28.00% 60.00%
1200-1600 33 16.50% 76.50%
1600-2000 26 13.00% 89.50%
2000-2400 11 5.50% 95.00%
2400-2800 3 1.50% 96.50%
2800-3200 3 1.50% 98.00%
More than 3200 4 2.00% 100.00%
Table 2a: Frequency distribution of the variable Utilities
Part 2B
The percentages of household spend on utilities can be given as:
1a. i. At most AUD $1200 per annum on utilities = 56/ 200 = 28%
1a. ii. Between AUD $1200 per annum and AUD $2400 per annum on utilities= (16.5 + 13 +
5.5) percent = 35%
1a. iii. more than AUD $2400 per annum on utilities = (1.5 + 1.5 + 2) percent = 5%
Task 2
Part 2A
Classes Frequency Percentage Cumm Percentage
0-400 19 9.50% 9.50%
400-800 45 22.50% 32.00%
800-1200 56 28.00% 60.00%
1200-1600 33 16.50% 76.50%
1600-2000 26 13.00% 89.50%
2000-2400 11 5.50% 95.00%
2400-2800 3 1.50% 96.50%
2800-3200 3 1.50% 98.00%
More than 3200 4 2.00% 100.00%
Table 2a: Frequency distribution of the variable Utilities
Part 2B
The percentages of household spend on utilities can be given as:
1a. i. At most AUD $1200 per annum on utilities = 56/ 200 = 28%
1a. ii. Between AUD $1200 per annum and AUD $2400 per annum on utilities= (16.5 + 13 +
5.5) percent = 35%
1a. iii. more than AUD $2400 per annum on utilities = (1.5 + 1.5 + 2) percent = 5%
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

7STATISTICS
Part 2C
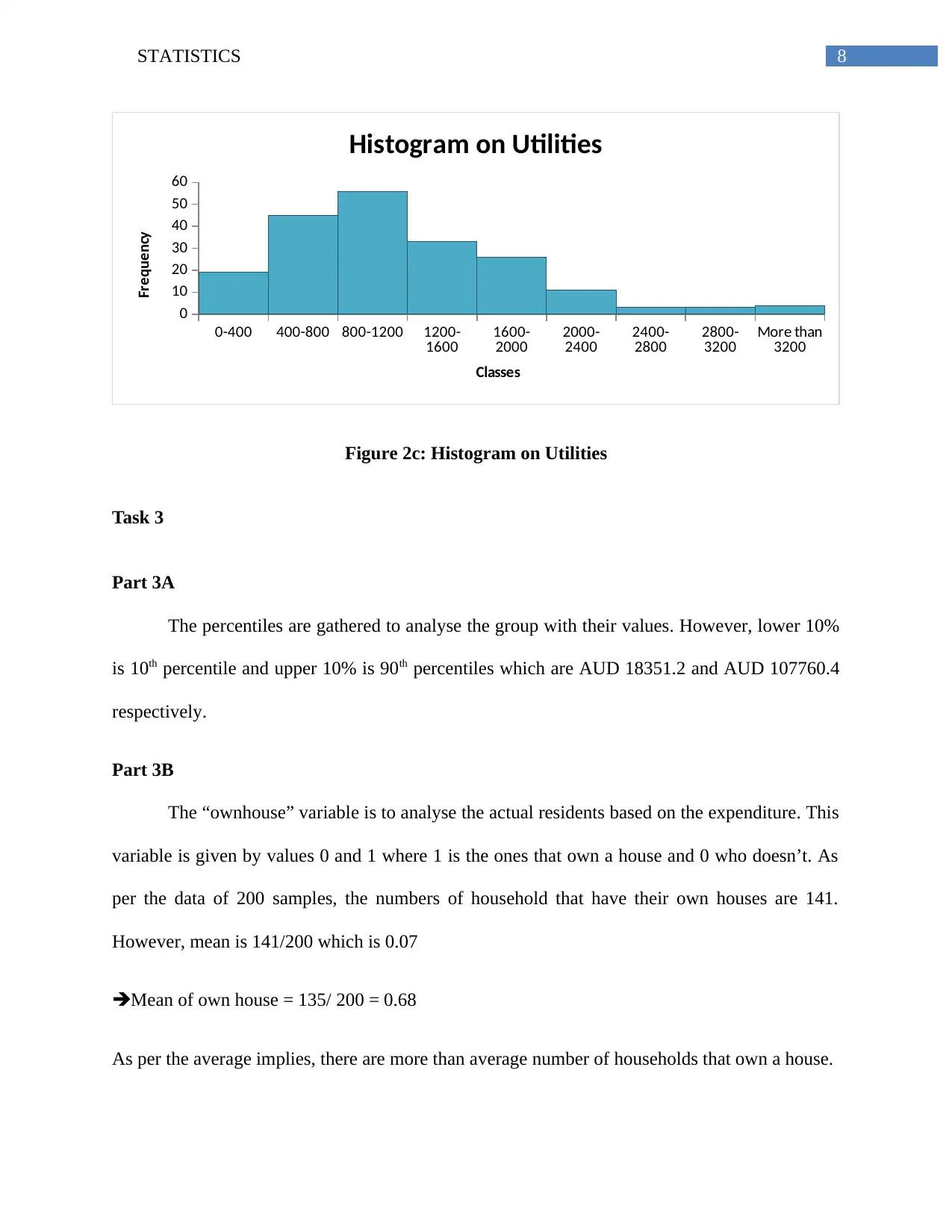
The interpretation can be done in two different ways. First is mathematically, where
mean, medina and mode are there to analyse the situation followed by histogram’s shape and
size.
As per mathematical distribution, a normal distribution has mean, mode and median all as
equal (Manley & Alberto, 2016). Whereas, in this case as per the table 2c given below; mean,
mode and median are not at all equal showing discrepancy. This depicts that the data is slightly
bend towards one side that is right side of the mean. In contrast, this household data on annual
expenditure on utilities is given as:
Mean of Utilities 1220
Median of Utilities 1100
Mode of Utilities 1000
Table 2c: Mathematical Interpretation on Utilities
Hence, Mean > median = mode, a positive bend whether the shape and size of the
histogram below is majorly shows a high on expenditure from 800-1200 AUD. However, in
histogram the data is on the left side depicting positive skewness (Corder & Foreman, 2014).
Part 2C
The interpretation can be done in two different ways. First is mathematically, where
mean, medina and mode are there to analyse the situation followed by histogram’s shape and
size.
As per mathematical distribution, a normal distribution has mean, mode and median all as
equal (Manley & Alberto, 2016). Whereas, in this case as per the table 2c given below; mean,
mode and median are not at all equal showing discrepancy. This depicts that the data is slightly
bend towards one side that is right side of the mean. In contrast, this household data on annual
expenditure on utilities is given as:
Mean of Utilities 1220
Median of Utilities 1100
Mode of Utilities 1000
Table 2c: Mathematical Interpretation on Utilities
Hence, Mean > median = mode, a positive bend whether the shape and size of the
histogram below is majorly shows a high on expenditure from 800-1200 AUD. However, in
histogram the data is on the left side depicting positive skewness (Corder & Foreman, 2014).
8STATISTICS
0-400 400-800 800-1200 1200-
1600 1600-
2000 2000-
2400 2400-
2800 2800-
3200 More than
3200
0
10
20
30
40
50
60
Histogram on Utilities
Classes
Frequency
Figure 2c: Histogram on Utilities
Task 3
Part 3A
The percentiles are gathered to analyse the group with their values. However, lower 10%
is 10th percentile and upper 10% is 90th percentiles which are AUD 18351.2 and AUD 107760.4
respectively.
Part 3B
The “ownhouse” variable is to analyse the actual residents based on the expenditure. This
variable is given by values 0 and 1 where 1 is the ones that own a house and 0 who doesn’t. As
per the data of 200 samples, the numbers of household that have their own houses are 141.
However, mean is 141/200 which is 0.07
Mean of own house = 135/ 200 = 0.68
As per the average implies, there are more than average number of households that own a house.
0-400 400-800 800-1200 1200-
1600 1600-
2000 2000-
2400 2400-
2800 2800-
3200 More than
3200
0
10
20
30
40
50
60
Histogram on Utilities
Classes
Frequency
Figure 2c: Histogram on Utilities
Task 3
Part 3A
The percentiles are gathered to analyse the group with their values. However, lower 10%
is 10th percentile and upper 10% is 90th percentiles which are AUD 18351.2 and AUD 107760.4
respectively.
Part 3B
The “ownhouse” variable is to analyse the actual residents based on the expenditure. This
variable is given by values 0 and 1 where 1 is the ones that own a house and 0 who doesn’t. As
per the data of 200 samples, the numbers of household that have their own houses are 141.
However, mean is 141/200 which is 0.07
Mean of own house = 135/ 200 = 0.68
As per the average implies, there are more than average number of households that own a house.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

9STATISTICS
Part 3C
Family size is calculated by adding adults and children together. However, the total
family size of 5 comes out to be 14. It has been calculated using the “COUNTIF” function in
excel. The probability of family size as 5 is given as:
Probability of “Family size =5” = 14/200 = 0.070
Part 3D
The scatter plot for log of (texp) against log of (ataxinc) is very well shown in figure 3d.
The plots shows a growing trend in the annual expenditure is growing against after tax annual
income. However, this indicates a growing demand of the resources like alcohol, meals, fuels,
etc. On the other hand, the correlation comes out to be 0.978187 shows they have strong
relationship. This positive correlation further emphasizes the effect that they may have on each
other in terms of expenditure (Cohen et al., 2013).
8.000 9.000 10.000 11.000 12.000 13.000 14.000
0.000
2.000
4.000
6.000
8.000
10.000
12.000
14.000
Scatter plot of Texp and ATaxInc
Relationship of two variables
Ln(Atexp)
Ln (ATaxInc)
Figure 3d: Scatter Plot of the two variables
Part 3C
Family size is calculated by adding adults and children together. However, the total
family size of 5 comes out to be 14. It has been calculated using the “COUNTIF” function in
excel. The probability of family size as 5 is given as:
Probability of “Family size =5” = 14/200 = 0.070
Part 3D
The scatter plot for log of (texp) against log of (ataxinc) is very well shown in figure 3d.
The plots shows a growing trend in the annual expenditure is growing against after tax annual
income. However, this indicates a growing demand of the resources like alcohol, meals, fuels,
etc. On the other hand, the correlation comes out to be 0.978187 shows they have strong
relationship. This positive correlation further emphasizes the effect that they may have on each
other in terms of expenditure (Cohen et al., 2013).
8.000 9.000 10.000 11.000 12.000 13.000 14.000
0.000
2.000
4.000
6.000
8.000
10.000
12.000
14.000
Scatter plot of Texp and ATaxInc
Relationship of two variables
Ln(Atexp)
Ln (ATaxInc)
Figure 3d: Scatter Plot of the two variables
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
10STATISTICS
Task 4
Part 4A
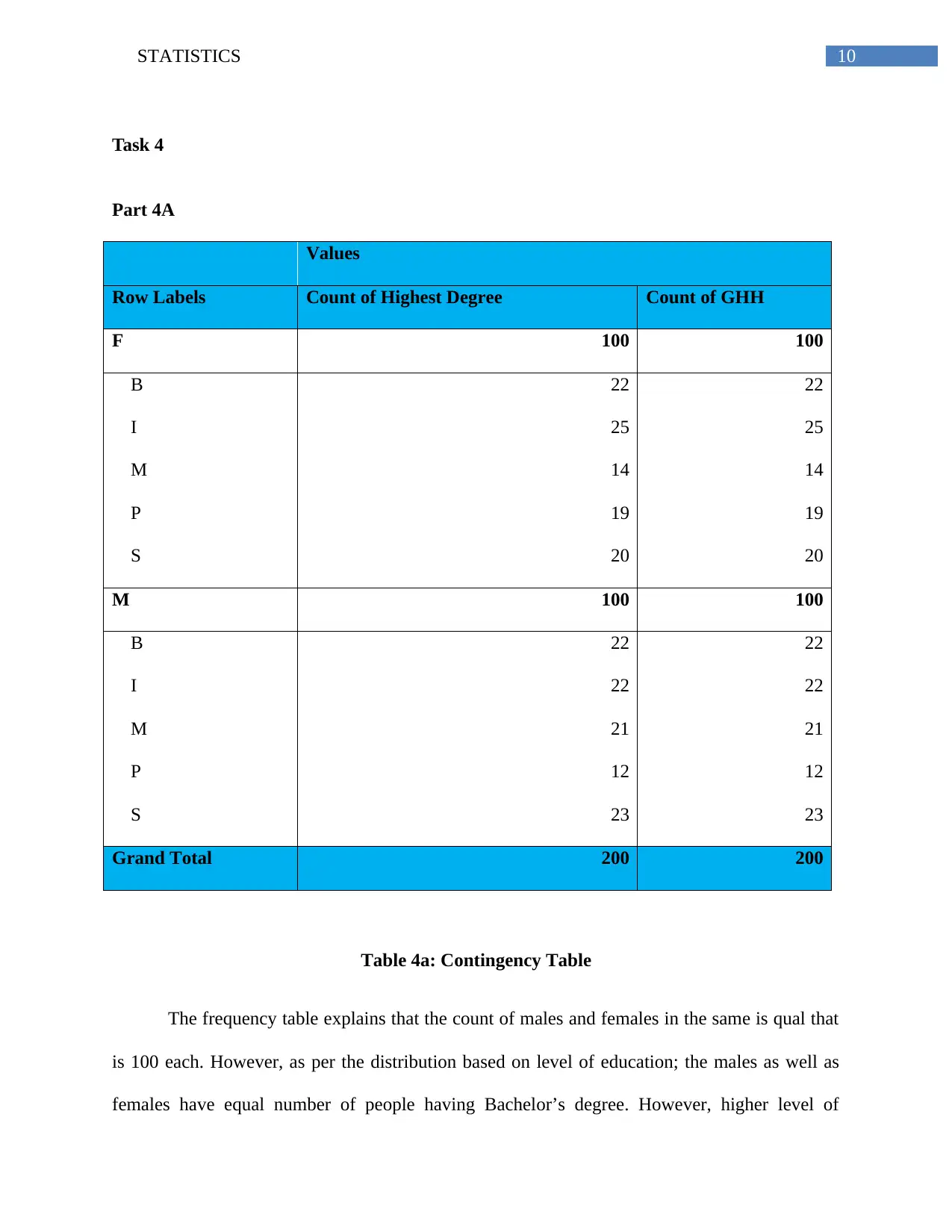
Values
Row Labels Count of Highest Degree Count of GHH
F 100 100
B 22 22
I 25 25
M 14 14
P 19 19
S 20 20
M 100 100
B 22 22
I 22 22
M 21 21
P 12 12
S 23 23
Grand Total 200 200
Table 4a: Contingency Table
The frequency table explains that the count of males and females in the same is qual that
is 100 each. However, as per the distribution based on level of education; the males as well as
females have equal number of people having Bachelor’s degree. However, higher level of
Task 4
Part 4A
Values
Row Labels Count of Highest Degree Count of GHH
F 100 100
B 22 22
I 25 25
M 14 14
P 19 19
S 20 20
M 100 100
B 22 22
I 22 22
M 21 21
P 12 12
S 23 23
Grand Total 200 200
Table 4a: Contingency Table
The frequency table explains that the count of males and females in the same is qual that
is 100 each. However, as per the distribution based on level of education; the males as well as
females have equal number of people having Bachelor’s degree. However, higher level of
11STATISTICS
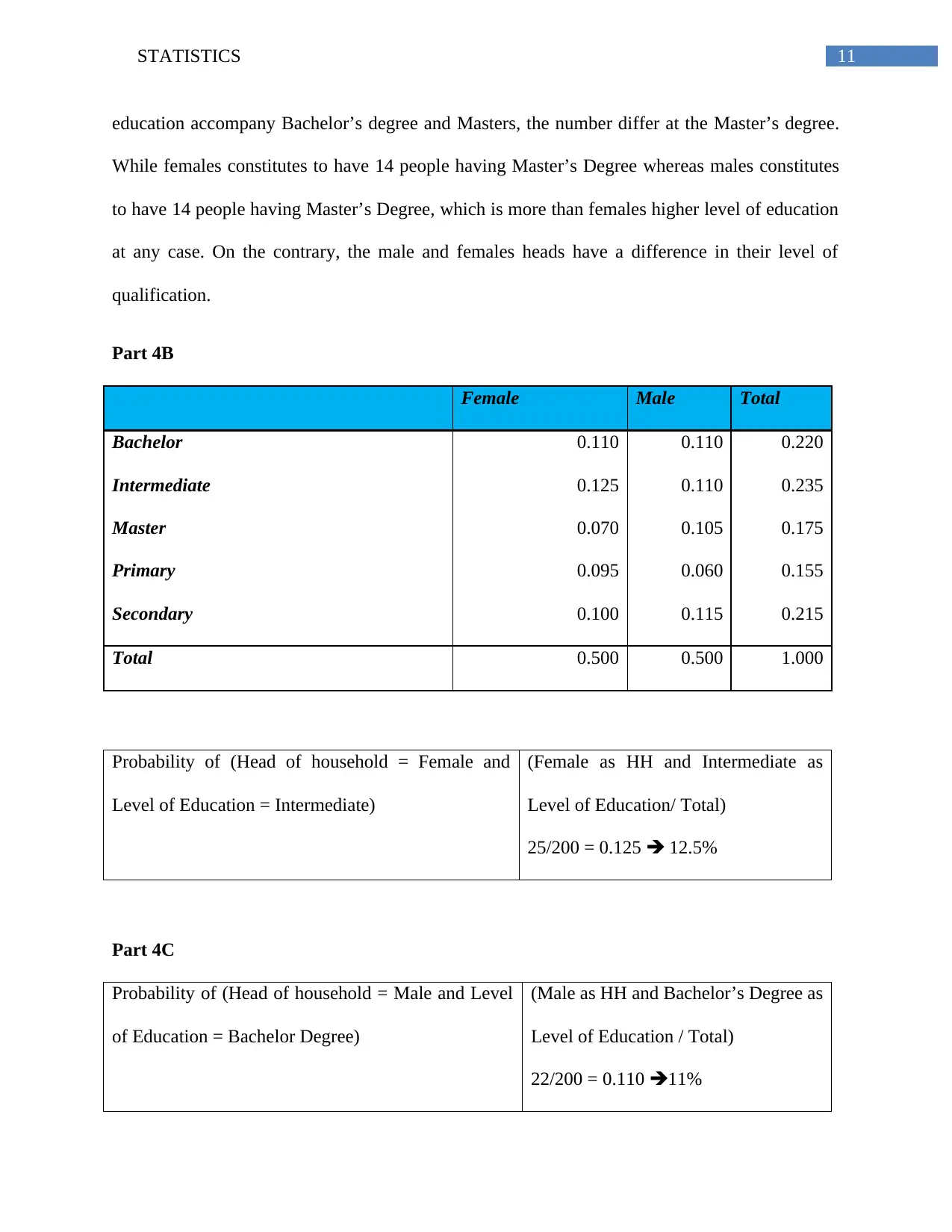
education accompany Bachelor’s degree and Masters, the number differ at the Master’s degree.
While females constitutes to have 14 people having Master’s Degree whereas males constitutes
to have 14 people having Master’s Degree, which is more than females higher level of education
at any case. On the contrary, the male and females heads have a difference in their level of
qualification.
Part 4B
Female Male Total
Bachelor 0.110 0.110 0.220
Intermediate 0.125 0.110 0.235
Master 0.070 0.105 0.175
Primary 0.095 0.060 0.155
Secondary 0.100 0.115 0.215
Total 0.500 0.500 1.000
Probability of (Head of household = Female and
Level of Education = Intermediate)
(Female as HH and Intermediate as
Level of Education/ Total)
25/200 = 0.125 12.5%
Part 4C
Probability of (Head of household = Male and Level
of Education = Bachelor Degree)
(Male as HH and Bachelor’s Degree as
Level of Education / Total)
22/200 = 0.110 11%
education accompany Bachelor’s degree and Masters, the number differ at the Master’s degree.
While females constitutes to have 14 people having Master’s Degree whereas males constitutes
to have 14 people having Master’s Degree, which is more than females higher level of education
at any case. On the contrary, the male and females heads have a difference in their level of
qualification.
Part 4B
Female Male Total
Bachelor 0.110 0.110 0.220
Intermediate 0.125 0.110 0.235
Master 0.070 0.105 0.175
Primary 0.095 0.060 0.155
Secondary 0.100 0.115 0.215
Total 0.500 0.500 1.000
Probability of (Head of household = Female and
Level of Education = Intermediate)
(Female as HH and Intermediate as
Level of Education/ Total)
25/200 = 0.125 12.5%
Part 4C
Probability of (Head of household = Male and Level
of Education = Bachelor Degree)
(Male as HH and Bachelor’s Degree as
Level of Education / Total)
22/200 = 0.110 11%
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 14
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.




